1.5 三角函数的应用 教学设计(表格式)北师大版数学九年级下册
文档属性
| 名称 | 1.5 三角函数的应用 教学设计(表格式)北师大版数学九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 21:36:51 | ||
图片预览




文档简介
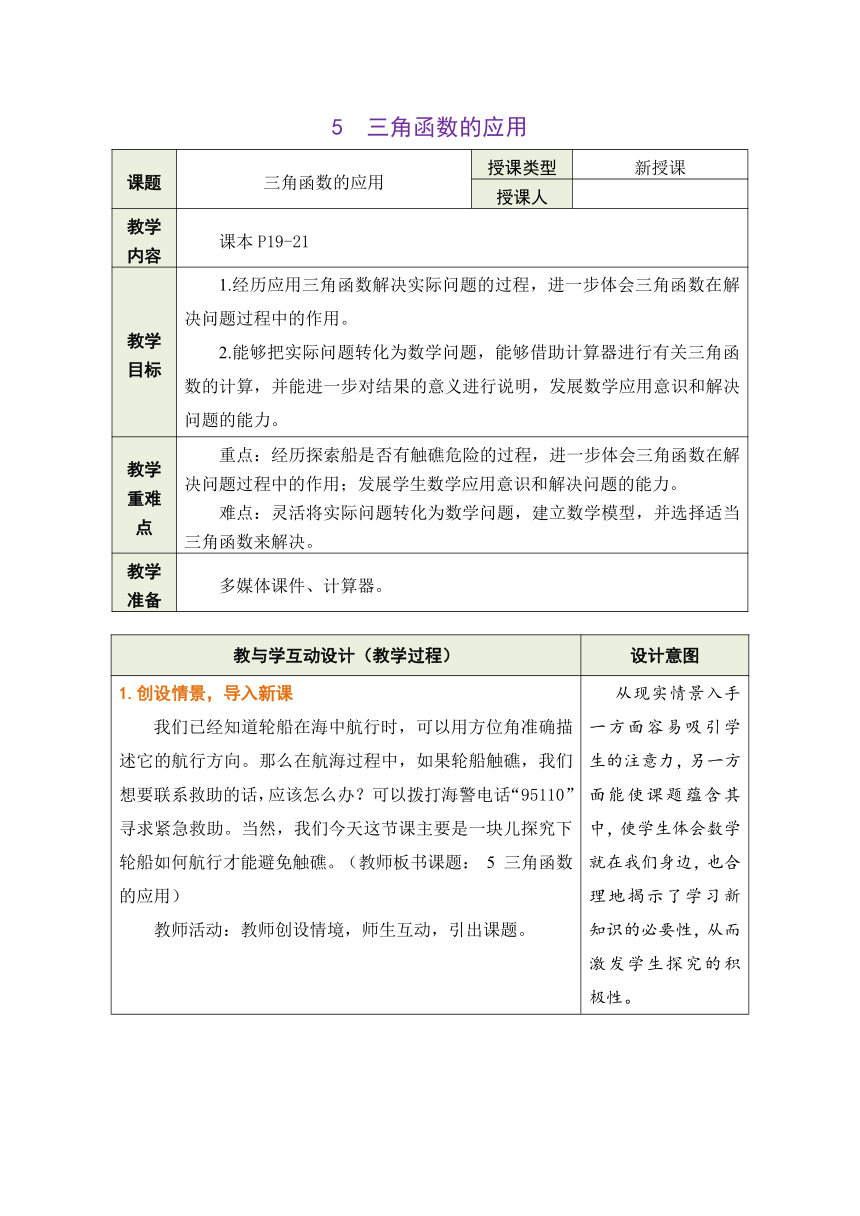
5 三角函数的应用
课题 三角函数的应用 授课类型 新授课
授课人
教学内容 课本P19-21
教学目标 1.经历应用三角函数解决实际问题的过程,进一步体会三角函数在解决问题过程中的作用。 2.能够把实际问题转化为数学问题,能够借助计算器进行有关三角函数的计算,并能进一步对结果的意义进行说明,发展数学应用意识和解决问题的能力。
教学重难点 重点:经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用;发展学生数学应用意识和解决问题的能力。 难点:灵活将实际问题转化为数学问题,建立数学模型,并选择适当三角函数来解决。
教学准备 多媒体课件、计算器。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向。那么在航海过程中,如果轮船触礁,我们想要联系救助的话,应该怎么办?可以拨打海警电话“95110”寻求紧急救助。当然,我们今天这节课主要是一块儿探究下轮船如何航行才能避免触礁。(教师板书课题: 5 三角函数的应用) 教师活动:教师创设情境,师生互动,引出课题。 从现实情景入手一方面容易吸引学生的注意力,另一方面能使课题蕴含其中,使学生体会数学就在我们身边,也合理地揭示了学习新知识的必要性,从而激发学生探究的积极性。
2.实践探究,学习新知 【探究1】 海中有一个小岛A,该岛四周10海里内有暗礁。今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行。 你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流。(多媒体呈现) 师生活动:教师提出问题,学生思考讨论回答。 教师:我们注意到题中有很多方位,请同学们根据题意首先在练习本上画出示意图。 学生:首先我们可将小岛A确定,货轮B在小岛A的南偏西55°的B处,C在B的正东方,且在A南偏东25°处。示意图如下。 教师:货轮要向正东方向继续行驶,有没有触礁的危险,由什么来决定? 学生:根据题意,小岛四周10海里内有暗礁,那么货轮继续向东航行,如果到小岛的最短距离大于10海里,则无触礁的危险,如果小于10海里则有触礁的危险。 教师:那么货轮继续向东航行途中会有触礁的危险吗? 学生:没有触礁的危险。过点A作BC的垂线,交直线BC于点D, 得到Rt△ABD和Rt△ACD。 ∴BD = AD tan 55°,CD = AD tan 25°, 由题意,得AD tan 55°- AD tan 25°= 20。 解得AD ≈ 20.79 n mile > 10 n mile,所以货轮没有触礁的危险。 【例题讲解】 如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1 m)。(多媒体呈现) 师生活动:教师出示问题,学生思考讨论,学生黑板演示,教师补充讲解。 学生:在Rt△BCD中,; 在Rt△ACD中,. 所以,CD≈43(m). 所以,该塔高43 m。 【探究2】 某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4 m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m) (多媒体呈现) 师生活动:教师出示问题,学生思考讨论,学生黑板演示,教师补充讲解。 学生:如图所示,作图,由已知条件可知,原来楼梯BD的长为4 m,高度BC为4 m,∠BDC=40°,改善后楼梯为AB,∠BAC=35°。 ∴BC=BDsin 40°=4 sin 40°m。 ∴AB=,AC=。 ∴AD-AD=, AC-CD=. 所以,调整后的楼梯会加长0.48 m,楼梯多占0.61 m长的一段地面。 【归纳总结】 师生活动:教师引导学生总结,板书呈现。 解题思路: 引导学生从实际问题中抽象出几何模型,进而通过解直角三角形解决问题。
3.学以致用,应用新知 考点 三角函数的应用 P20 随堂练习1,2 变式训练 深圳是沿海城市,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距深圳正南200千米的A处有一台风中心,中心最大风力为12级,每远离台风中心30千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东43°方向向B移动,且台风中心风力不变,若城市受到风力超过六级,则称受台风影响. (1)此次台风会不会影响深圳?为什么? (2)若受到影响,那么受到台风影响的最大风力为几级? (3)若受到影响,那么此次台风影响深圳共持续多长时间?(结果可带根号表示)(sin 43°,cos 42°,tan 42°) 解:(1)该城市会受到这次台风的影响. 理由如下: 如图,过C作CD⊥BA于D。 在Rt△ACD中, ∵∠CAD=43°,AC=200千米, ∴CD=AC sin43°≈200150(千米)。 ∵城市受到的风力超过六级,则称受台风影响, ∴受台风影响范围的半径为30×(12﹣6)=180(千米), ∵150(千米)<180(千米), ∴该城市会受到这次台风的影响。 (2)∵CD距台风中心最近, ∴该城市受到这次台风最大风力为:12﹣(150÷30)=7(级)。 答:受到台风影响的最大风力为7级。 (3)如图以C为圆心,180为半径作⊙A交BC于E,F。 则CE=CF=180。 ∴台风影响该市持续的路程为:EF=2DE=260(千米)。 ∴台风影响该市的持续时间:t=6020=3(时); 答:台风影响该城市的持续时间为3小时。 通过基本的练习以及变式训练,在巩固学生本节所学知识的基础上,进一步提升学生使用三角函数解决实际问题的能力。
4.随堂训练,巩固新知 1. 如图,点A到点C的距离为200米,要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( ) A.100米 B.200米 C.米 D.100米 答案:D 某次台风来袭时,一棵笔直大树树干AB(树干AB垂直于水平地面)被刮倾斜后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,∠ACD=60°,AD=5米,求这棵大树AB的高度。(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,1.73) 解:过点A作AE⊥CD于点E,则∠AEC=∠AED=90°。 ∵在Rt△AED中,∠ADC=37°, ∴cos37°0.8, ∴DE=4。 ∵sin37°0.6,∴AE=3。 在Rt△AEC中, ∵∠CAE=90°﹣∠ACE=90°﹣60°=30°, ∴CEAE, ∴AC=2CE=2, ∴AB=AC+CE+ED=24=34≈9.2(米)。 答:这棵大树AB原来的高度约是9.2米。 图1是一辆自卸式货车,卸渣土的过程主要是由车架上的液压油缸将车厢向上推,车厢里的渣土即可自动倒出,图2是其抽象示意图,AB为车架,AC为车厢(假设车架与车厢的长度相等),OD为液压油缸,已知AB=4米,当液压油缸OD将车厢AC推至与车架AB的夹角∠CAB=37°时,点O、D恰好为AB,AC的中点,此时车内渣土可全部倒出.(结果精确到0.1米) (1)求此时点C距离车架AB的高度; (2)求此时液压油缸OD的长度。 (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,3.16) 解:(1)过点C作CE⊥AB,垂足为E,∴∠AEC=90°。 在Rt△AEC中,∠A=37°,AC=4米, ∴CE=AC sin37°≈4×0.6=2.4(米)。 ∴此时点C距离车架AB的高度约为2.4米。 (2)过点D作DF⊥AO,垂足为F, ∴∠AFD=∠DFO=90°。 ∵点D为AC的中点,点O为AB的中点, ∴ADAC=2(米),AOAB=2(米)。 在Rt△ADF中,∠A=37°, ∴DF=AD sin37°≈2×0.6=1.2(米), AF=AD cos37°≈2×0.8=1.6(米), ∴OF=AO﹣AF=0.4(米), 在Rt△DFO中,OD1.3(米), ∴此时液压油缸OD的长度约为1.3米。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1. 如何把实际问题转化为数学问题(画出示意图); 2. 解决三角函数应用的一般思路。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P21习题1.6。 课后练习巩固,让学生所学知识得以运用,提高利用三角函数解决实际问题的能力。
板书设计 5 三角函数的应用一、解觉三角形三角函数应用的一般思路教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 从实际问题入手,培养学生的运用意识和转化思想,建立数学与生活的联系,能把生活问题数学化,会用数学的眼光去分析问题,解决问题。 从教学过程设计上看,对各个问题的解决都充满了观察、猜想、推理和交流等丰富多彩的数学活动,学生不仅获得了计算能力,而更重要的是获得了自己去探究数学的体验和利用数学去解决实际问题的能力,从而激发学习兴趣。 教师在教学中要充分关注学生思维的变化,抓住时机对学生进行启发引导,使学生能用数学的眼光去观察现实生活问题,建立数学模型,真正体现数学来源于生活又服务于生活这一思想。 反思,更进一步提升。
课题 三角函数的应用 授课类型 新授课
授课人
教学内容 课本P19-21
教学目标 1.经历应用三角函数解决实际问题的过程,进一步体会三角函数在解决问题过程中的作用。 2.能够把实际问题转化为数学问题,能够借助计算器进行有关三角函数的计算,并能进一步对结果的意义进行说明,发展数学应用意识和解决问题的能力。
教学重难点 重点:经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用;发展学生数学应用意识和解决问题的能力。 难点:灵活将实际问题转化为数学问题,建立数学模型,并选择适当三角函数来解决。
教学准备 多媒体课件、计算器。
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 我们已经知道轮船在海中航行时,可以用方位角准确描述它的航行方向。那么在航海过程中,如果轮船触礁,我们想要联系救助的话,应该怎么办?可以拨打海警电话“95110”寻求紧急救助。当然,我们今天这节课主要是一块儿探究下轮船如何航行才能避免触礁。(教师板书课题: 5 三角函数的应用) 教师活动:教师创设情境,师生互动,引出课题。 从现实情景入手一方面容易吸引学生的注意力,另一方面能使课题蕴含其中,使学生体会数学就在我们身边,也合理地揭示了学习新知识的必要性,从而激发学生探究的积极性。
2.实践探究,学习新知 【探究1】 海中有一个小岛A,该岛四周10海里内有暗礁。今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行。 你认为货轮继续向东航行途中会有触礁的危险吗?你是如何想的?与同伴进行交流。(多媒体呈现) 师生活动:教师提出问题,学生思考讨论回答。 教师:我们注意到题中有很多方位,请同学们根据题意首先在练习本上画出示意图。 学生:首先我们可将小岛A确定,货轮B在小岛A的南偏西55°的B处,C在B的正东方,且在A南偏东25°处。示意图如下。 教师:货轮要向正东方向继续行驶,有没有触礁的危险,由什么来决定? 学生:根据题意,小岛四周10海里内有暗礁,那么货轮继续向东航行,如果到小岛的最短距离大于10海里,则无触礁的危险,如果小于10海里则有触礁的危险。 教师:那么货轮继续向东航行途中会有触礁的危险吗? 学生:没有触礁的危险。过点A作BC的垂线,交直线BC于点D, 得到Rt△ABD和Rt△ACD。 ∴BD = AD tan 55°,CD = AD tan 25°, 由题意,得AD tan 55°- AD tan 25°= 20。 解得AD ≈ 20.79 n mile > 10 n mile,所以货轮没有触礁的危险。 【例题讲解】 如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1 m)。(多媒体呈现) 师生活动:教师出示问题,学生思考讨论,学生黑板演示,教师补充讲解。 学生:在Rt△BCD中,; 在Rt△ACD中,. 所以,CD≈43(m). 所以,该塔高43 m。 【探究2】 某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4 m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m) (多媒体呈现) 师生活动:教师出示问题,学生思考讨论,学生黑板演示,教师补充讲解。 学生:如图所示,作图,由已知条件可知,原来楼梯BD的长为4 m,高度BC为4 m,∠BDC=40°,改善后楼梯为AB,∠BAC=35°。 ∴BC=BDsin 40°=4 sin 40°m。 ∴AB=,AC=。 ∴AD-AD=, AC-CD=. 所以,调整后的楼梯会加长0.48 m,楼梯多占0.61 m长的一段地面。 【归纳总结】 师生活动:教师引导学生总结,板书呈现。 解题思路: 引导学生从实际问题中抽象出几何模型,进而通过解直角三角形解决问题。
3.学以致用,应用新知 考点 三角函数的应用 P20 随堂练习1,2 变式训练 深圳是沿海城市,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距深圳正南200千米的A处有一台风中心,中心最大风力为12级,每远离台风中心30千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东43°方向向B移动,且台风中心风力不变,若城市受到风力超过六级,则称受台风影响. (1)此次台风会不会影响深圳?为什么? (2)若受到影响,那么受到台风影响的最大风力为几级? (3)若受到影响,那么此次台风影响深圳共持续多长时间?(结果可带根号表示)(sin 43°,cos 42°,tan 42°) 解:(1)该城市会受到这次台风的影响. 理由如下: 如图,过C作CD⊥BA于D。 在Rt△ACD中, ∵∠CAD=43°,AC=200千米, ∴CD=AC sin43°≈200150(千米)。 ∵城市受到的风力超过六级,则称受台风影响, ∴受台风影响范围的半径为30×(12﹣6)=180(千米), ∵150(千米)<180(千米), ∴该城市会受到这次台风的影响。 (2)∵CD距台风中心最近, ∴该城市受到这次台风最大风力为:12﹣(150÷30)=7(级)。 答:受到台风影响的最大风力为7级。 (3)如图以C为圆心,180为半径作⊙A交BC于E,F。 则CE=CF=180。 ∴台风影响该市持续的路程为:EF=2DE=260(千米)。 ∴台风影响该市的持续时间:t=6020=3(时); 答:台风影响该城市的持续时间为3小时。 通过基本的练习以及变式训练,在巩固学生本节所学知识的基础上,进一步提升学生使用三角函数解决实际问题的能力。
4.随堂训练,巩固新知 1. 如图,点A到点C的距离为200米,要测量河对岸B点到河岸AD的距离.小明在A点测得B在北偏东60°的方向上,在C点测得B在北偏东30°的方向上,则B点到河岸AD的距离为( ) A.100米 B.200米 C.米 D.100米 答案:D 某次台风来袭时,一棵笔直大树树干AB(树干AB垂直于水平地面)被刮倾斜后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,∠ACD=60°,AD=5米,求这棵大树AB的高度。(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,1.73) 解:过点A作AE⊥CD于点E,则∠AEC=∠AED=90°。 ∵在Rt△AED中,∠ADC=37°, ∴cos37°0.8, ∴DE=4。 ∵sin37°0.6,∴AE=3。 在Rt△AEC中, ∵∠CAE=90°﹣∠ACE=90°﹣60°=30°, ∴CEAE, ∴AC=2CE=2, ∴AB=AC+CE+ED=24=34≈9.2(米)。 答:这棵大树AB原来的高度约是9.2米。 图1是一辆自卸式货车,卸渣土的过程主要是由车架上的液压油缸将车厢向上推,车厢里的渣土即可自动倒出,图2是其抽象示意图,AB为车架,AC为车厢(假设车架与车厢的长度相等),OD为液压油缸,已知AB=4米,当液压油缸OD将车厢AC推至与车架AB的夹角∠CAB=37°时,点O、D恰好为AB,AC的中点,此时车内渣土可全部倒出.(结果精确到0.1米) (1)求此时点C距离车架AB的高度; (2)求此时液压油缸OD的长度。 (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,3.16) 解:(1)过点C作CE⊥AB,垂足为E,∴∠AEC=90°。 在Rt△AEC中,∠A=37°,AC=4米, ∴CE=AC sin37°≈4×0.6=2.4(米)。 ∴此时点C距离车架AB的高度约为2.4米。 (2)过点D作DF⊥AO,垂足为F, ∴∠AFD=∠DFO=90°。 ∵点D为AC的中点,点O为AB的中点, ∴ADAC=2(米),AOAB=2(米)。 在Rt△ADF中,∠A=37°, ∴DF=AD sin37°≈2×0.6=1.2(米), AF=AD cos37°≈2×0.8=1.6(米), ∴OF=AO﹣AF=0.4(米), 在Rt△DFO中,OD1.3(米), ∴此时液压油缸OD的长度约为1.3米。 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 1. 如何把实际问题转化为数学问题(画出示意图); 2. 解决三角函数应用的一般思路。 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P21习题1.6。 课后练习巩固,让学生所学知识得以运用,提高利用三角函数解决实际问题的能力。
板书设计 5 三角函数的应用一、解觉三角形三角函数应用的一般思路教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 从实际问题入手,培养学生的运用意识和转化思想,建立数学与生活的联系,能把生活问题数学化,会用数学的眼光去分析问题,解决问题。 从教学过程设计上看,对各个问题的解决都充满了观察、猜想、推理和交流等丰富多彩的数学活动,学生不仅获得了计算能力,而更重要的是获得了自己去探究数学的体验和利用数学去解决实际问题的能力,从而激发学习兴趣。 教师在教学中要充分关注学生思维的变化,抓住时机对学生进行启发引导,使学生能用数学的眼光去观察现实生活问题,建立数学模型,真正体现数学来源于生活又服务于生活这一思想。 反思,更进一步提升。
