2.2.3 二次函数的图象与性质 教学设计(表格式)北师大版数学九年级下册
文档属性
| 名称 | 2.2.3 二次函数的图象与性质 教学设计(表格式)北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 00:00:00 | ||
图片预览



文档简介
2 二次函数的图象与性质(第3课时)
课题 二次函数的图象与性质(第3课时) 授课类型 新授课
授课人
教学内容 课本P36-39
教学目标 能够作出y=a(x-h)2和y=a(x-h)2+k的图象,理解它们与y=ax2的图象的关系,理解a,h,k对二次函数图象的影响。 能正确找出y=a(x-h)2+k的图象的开口方向、对称轴、顶点坐标。
教学重难点 重点:二次函数y=a(x-h)2+k的图象与性质。 难点:理解二次函数y=a(x-h)2和y=a(x-h)2+k图象之间的关系,理解二次函数y=a(x-h)2+k中a,h,k对函数图象的影响。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情境,导入新课 我们已学习过两种类型的二次函数,y=ax2与y=ax2+c,知道它们都是轴对称图形,对称轴是y轴,顶点都是原点。还知道函数y=ax2的图象经过上下移动可以得到y=ax2+c的图象是,那么如果将函数y=ax2的图象左右移动,我们会得到什么样的函数形式,它又有哪些性质 本节课我们就来研究有关问题。(板书课题:二次函数的图象与性质 第3课时) 通过二次函数y=ax2+c的图象可以由y=ax2经过上下平移得到,设问y=ax2经过左右平移会得到怎样的函数形式,进而引出本节课课题。
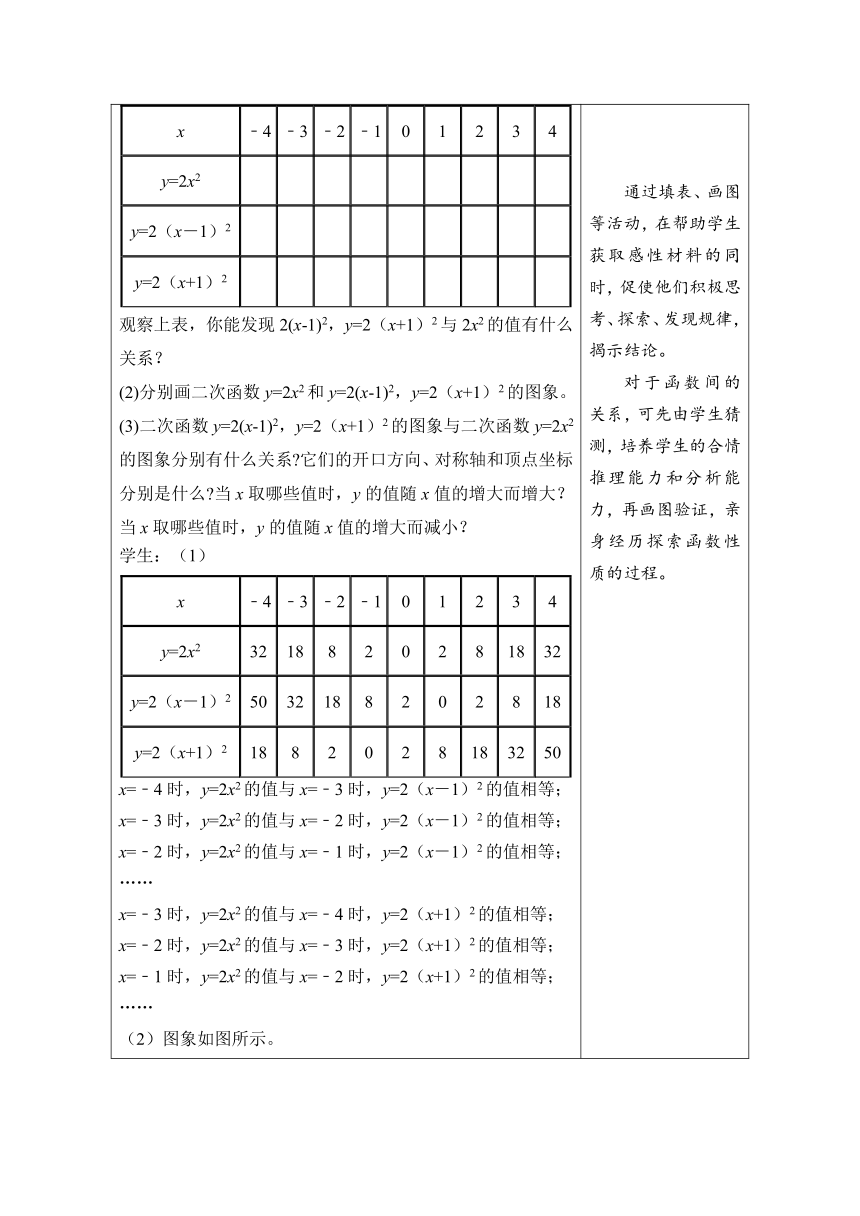
2.实践探究,学习新知 【探究1】二次函数y=a(x-h)2的图象与性质 教师:在平面直角坐标系中作二次函数y=2x2,y=2(x-1)2和y=2(x+1)2的图象。(多媒体呈现) (1)完成下表: x﹣4﹣3﹣2﹣101234y=2x2y=2(x-1)2y=2(x+1)2
观察上表,你能发现2(x-1)2,y=2(x+1)2与2x2的值有什么关系? (2)分别画二次函数y=2x2和y=2(x-1)2,y=2(x+1)2的图象。 (3)二次函数y=2(x-1)2,y=2(x+1)2的图象与二次函数y=2x2的图象分别有什么关系 它们的开口方向、对称轴和顶点坐标分别是什么 当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小? 学生:(1) x﹣4﹣3﹣2﹣101234y=2x23218820281832y=2(x-1)25032188202818y=2(x+1)21882028183250
x=﹣4时,y=2x2的值与x=﹣3时,y=2(x-1)2的值相等; x=﹣3时,y=2x2的值与x=﹣2时,y=2(x-1)2的值相等; x=﹣2时,y=2x2的值与x=﹣1时,y=2(x-1)2的值相等; …… x=﹣3时,y=2x2的值与x=﹣4时,y=2(x+1)2的值相等; x=﹣2时,y=2x2的值与x=﹣3时,y=2(x+1)2的值相等; x=﹣1时,y=2x2的值与x=﹣2时,y=2(x+1)2的值相等; …… (2)图象如图所示。 (3)根据列表及图象可得,二次函数y=2(x-1)2,y=2(x+1)2的图象与二次函数y=2x2的图象形状相同,且二次函数y=2(x-1)2的图象可由二次函数y=2x2的图象向右平移1个单位长度获得,二次函数y=2(x+1)2的图象可由二次函数y=2x2的图象向左平移1个单位长度获得。 二次函数y=2(x-1)2图象的开口方向、对称轴和顶点坐标如下表所示。 函数表达式y=2(x-1)2y=2(x+1)2开口方向向上向上对称轴直线x=1直线x=-1顶点坐标(1,0)(-1,0)增减性当x<1时,y随x的增大而减小; 当x>1时,y随x的增大而增大当x<-1时,y随x的增大而减小; 当x>-1时,y随x的增大而增大
【归纳总结】 二次函数y=a(x-h)2的图象与性质 函数表达式y=a(x-h)2(a<0)y=a(x-h)2(a>0)开口方向向下向上对称轴直线x=h顶点坐标(h,0)增减性当x<h时,y随x的增大而增大; 当x>h时,y随x的增大而减小当x<h时,y随x的增大而减小; 当x>h时,y随x的增大而增大
二次函数y=a(x-h)2与y=ax2的图象之间的关系 当h>0时,将二次函数y=ax2的图象向右平移h个单位长度,得到y=a(x-h)2的图象; 当h<0时,将二次函数y=ax2的图象向左平移|h|个单位长度,得到y=a(x-h)2的图象。 【探究2】二次函数y=a(x-h)2+k的图象与性质 教师:猜一猜,二次函数y=2(x+1)2-3的图象,可以由y=2x2的图象平移得到吗?请说明平移方法,并通过画图验证。 学生:可以。将二次函数y=2x2的图象先向左平移1个单位,再向下平移3个单位,就可以得到二次函数y=2(x+1)2-3的图象。 列表如下。 x﹣4﹣3﹣2﹣101234y=2x23218820281832y=2(x+1)2-3155-1-3-15152947
画图如下。 教师追问:那么, 二次函数y=a(x-h)2+k的图象可以由y=ax2的图象平移得到吗?如何平移。 学生:①当h>0,k>0时,二次函数y=ax2的图象先向右平移h个单位长度,再向上平移k个单位长度,可以得到二次函数y=a(x-h)2+k的图象; ②当h>0,k<0时,二次函数y=ax2的图象先向右平移h个单位长度,再向下平移|k|个单位长度,可以得到二次函数y=a(x-h)2+k的图象; ①当h<0,k>0时,二次函数y=ax2的图象先向左平移|h|个单位长度,再向上平移k个单位长度,可以得到二次函数y=a(x-h)2+k的图象; ①当h<0,k<0时,二次函数y=ax2的图象先向左平移|h|个单位长度,再向下平移|k|个单位长度,可以得到二次函数y=a(x-h)2+k的图象。 教师:由图象变化推得表达式的变化,我们可简记为:左加右减,上加下减。由平移,我们可以得到二次函数y=a(x-h)2+k的图象性质,请完成下表。(多媒体呈现) 学生: 抛物线y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)开口方向向上向下顶点坐标(h,k)对称轴x=h增减性当x<h时,y随x的增大而增大; 当x>h时,y随x的增大而减小当x<h时,y随x的增大而减小; 当x>h时,y随x的增大而增大最值当x=h时,y有最小值为k当x=h时,y有最大值为k
通过填表、画图等活动,在帮助学生获取感性材料的同时,促使他们积极思考、探索、发现规律,揭示结论。 对于函数间的关系,可先由学生猜测,培养学生的合情推理能力和分析能力,再画图验证,亲身经历探索函数性质的过程。
3.学以致用,应用新知 考点 二次函数的图象与性质 P38随堂练习 变式训练 y=a(x﹣h)2+k的图象可以看成y=ax2的图象先沿x轴整体左(右)平移 个单位: 当h>O时,向 平移; 当h<0时,向 平移.再沿对称轴整体上(下)平移 个单位:当k>O时,向 平移; 当k<0时,向下平移.因此,二次函数y=a(x﹣h)2+k的图象是一条抛物线,它的开口方向由 值决定,对称轴为 ,顶点坐标为 。 答案:右 左 |k| 上a 直线x=h (h,k) 在知识梳理的基础上,通过及时的练习,进一步提升学生对二次函数的图象与性质的理解掌握,同时教师可根据学生的掌握情况及时讲解。
4.随堂训练,巩固新知 1. 关于抛物线y=(x﹣1)2﹣2,下列说法错误的是( ) A.开口方向向上 B.对称轴是直线x=1 C.顶点坐标为(﹣1,﹣2) D.当x>1时,y随x的增大而增大 答案:C 2. 如图,已知二次函数y=(x+1)2﹣4,当﹣2≤x≤2时,则函数y的最小值和最大值( ) A.﹣3和5 B.﹣4和5 C.﹣4和﹣3 D.﹣1和5 答案:B 3.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=3(x+1)2+4m(m为常数)上的三点,则y1,y2,y3的大小关系为( ) A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1 答案:A 4.点A(m﹣1,y1),B(m,y2)都在二次函数y=(x﹣1)2+n的图象上.若y1<y2,则m的取值范围为( ) A.m>2 B.m C.m<1 D.m<2 答案:B 5.小嘉说:将二次函数y=x2的图象平移或翻折后经过点(2,0)有4种方法: ①向右平移2个单位长度 ②向右平移1个单位长度,再向下平移1个单位长度 ③向下平移4个单位长度 ④沿x轴翻折,再向上平移4个单位长度 你认为小嘉说的方法中正确的个数有( ) A.1个 B.2个 C.3个 D.4个 答案:D 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 二次函数y=a(x-h)2和y=a(x-h)2+k图象的性质; 二次函数y=ax2,y=a(x-h)2,y=a(x-h)2+k图象之间的关系。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:P39 习题2.4。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 二次函数的图象与性质(第3课时)二次函数y=a(x-h)2 二次函数y=a(x-h)2+k 平移教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课采用教师引导,学生自主探索和小组合作相结合的教学方式。本课时还课堂于学生,在开放的前提下,让学生经历动手画图、合作交流的过程,给学生一个充分发表见解的舞台,激发学生的创新精神,提高学生的自信力,打造高效课堂! 在学生的探究过程中,教师要注意引导学生进行图象和图象之间的比较、表达式和表达式之间的比较,建立图象和表达式之间的联系, 是否理解表达式的变化将引起图象的何种变化,或者图象的变化将要引起表达式的何种变化。 要引导学生从感性认识上升到理性认识。 反思,更进一步提升。
课题 二次函数的图象与性质(第3课时) 授课类型 新授课
授课人
教学内容 课本P36-39
教学目标 能够作出y=a(x-h)2和y=a(x-h)2+k的图象,理解它们与y=ax2的图象的关系,理解a,h,k对二次函数图象的影响。 能正确找出y=a(x-h)2+k的图象的开口方向、对称轴、顶点坐标。
教学重难点 重点:二次函数y=a(x-h)2+k的图象与性质。 难点:理解二次函数y=a(x-h)2和y=a(x-h)2+k图象之间的关系,理解二次函数y=a(x-h)2+k中a,h,k对函数图象的影响。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情境,导入新课 我们已学习过两种类型的二次函数,y=ax2与y=ax2+c,知道它们都是轴对称图形,对称轴是y轴,顶点都是原点。还知道函数y=ax2的图象经过上下移动可以得到y=ax2+c的图象是,那么如果将函数y=ax2的图象左右移动,我们会得到什么样的函数形式,它又有哪些性质 本节课我们就来研究有关问题。(板书课题:二次函数的图象与性质 第3课时) 通过二次函数y=ax2+c的图象可以由y=ax2经过上下平移得到,设问y=ax2经过左右平移会得到怎样的函数形式,进而引出本节课课题。
2.实践探究,学习新知 【探究1】二次函数y=a(x-h)2的图象与性质 教师:在平面直角坐标系中作二次函数y=2x2,y=2(x-1)2和y=2(x+1)2的图象。(多媒体呈现) (1)完成下表: x﹣4﹣3﹣2﹣101234y=2x2y=2(x-1)2y=2(x+1)2
观察上表,你能发现2(x-1)2,y=2(x+1)2与2x2的值有什么关系? (2)分别画二次函数y=2x2和y=2(x-1)2,y=2(x+1)2的图象。 (3)二次函数y=2(x-1)2,y=2(x+1)2的图象与二次函数y=2x2的图象分别有什么关系 它们的开口方向、对称轴和顶点坐标分别是什么 当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小? 学生:(1) x﹣4﹣3﹣2﹣101234y=2x23218820281832y=2(x-1)25032188202818y=2(x+1)21882028183250
x=﹣4时,y=2x2的值与x=﹣3时,y=2(x-1)2的值相等; x=﹣3时,y=2x2的值与x=﹣2时,y=2(x-1)2的值相等; x=﹣2时,y=2x2的值与x=﹣1时,y=2(x-1)2的值相等; …… x=﹣3时,y=2x2的值与x=﹣4时,y=2(x+1)2的值相等; x=﹣2时,y=2x2的值与x=﹣3时,y=2(x+1)2的值相等; x=﹣1时,y=2x2的值与x=﹣2时,y=2(x+1)2的值相等; …… (2)图象如图所示。 (3)根据列表及图象可得,二次函数y=2(x-1)2,y=2(x+1)2的图象与二次函数y=2x2的图象形状相同,且二次函数y=2(x-1)2的图象可由二次函数y=2x2的图象向右平移1个单位长度获得,二次函数y=2(x+1)2的图象可由二次函数y=2x2的图象向左平移1个单位长度获得。 二次函数y=2(x-1)2图象的开口方向、对称轴和顶点坐标如下表所示。 函数表达式y=2(x-1)2y=2(x+1)2开口方向向上向上对称轴直线x=1直线x=-1顶点坐标(1,0)(-1,0)增减性当x<1时,y随x的增大而减小; 当x>1时,y随x的增大而增大当x<-1时,y随x的增大而减小; 当x>-1时,y随x的增大而增大
【归纳总结】 二次函数y=a(x-h)2的图象与性质 函数表达式y=a(x-h)2(a<0)y=a(x-h)2(a>0)开口方向向下向上对称轴直线x=h顶点坐标(h,0)增减性当x<h时,y随x的增大而增大; 当x>h时,y随x的增大而减小当x<h时,y随x的增大而减小; 当x>h时,y随x的增大而增大
二次函数y=a(x-h)2与y=ax2的图象之间的关系 当h>0时,将二次函数y=ax2的图象向右平移h个单位长度,得到y=a(x-h)2的图象; 当h<0时,将二次函数y=ax2的图象向左平移|h|个单位长度,得到y=a(x-h)2的图象。 【探究2】二次函数y=a(x-h)2+k的图象与性质 教师:猜一猜,二次函数y=2(x+1)2-3的图象,可以由y=2x2的图象平移得到吗?请说明平移方法,并通过画图验证。 学生:可以。将二次函数y=2x2的图象先向左平移1个单位,再向下平移3个单位,就可以得到二次函数y=2(x+1)2-3的图象。 列表如下。 x﹣4﹣3﹣2﹣101234y=2x23218820281832y=2(x+1)2-3155-1-3-15152947
画图如下。 教师追问:那么, 二次函数y=a(x-h)2+k的图象可以由y=ax2的图象平移得到吗?如何平移。 学生:①当h>0,k>0时,二次函数y=ax2的图象先向右平移h个单位长度,再向上平移k个单位长度,可以得到二次函数y=a(x-h)2+k的图象; ②当h>0,k<0时,二次函数y=ax2的图象先向右平移h个单位长度,再向下平移|k|个单位长度,可以得到二次函数y=a(x-h)2+k的图象; ①当h<0,k>0时,二次函数y=ax2的图象先向左平移|h|个单位长度,再向上平移k个单位长度,可以得到二次函数y=a(x-h)2+k的图象; ①当h<0,k<0时,二次函数y=ax2的图象先向左平移|h|个单位长度,再向下平移|k|个单位长度,可以得到二次函数y=a(x-h)2+k的图象。 教师:由图象变化推得表达式的变化,我们可简记为:左加右减,上加下减。由平移,我们可以得到二次函数y=a(x-h)2+k的图象性质,请完成下表。(多媒体呈现) 学生: 抛物线y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)开口方向向上向下顶点坐标(h,k)对称轴x=h增减性当x<h时,y随x的增大而增大; 当x>h时,y随x的增大而减小当x<h时,y随x的增大而减小; 当x>h时,y随x的增大而增大最值当x=h时,y有最小值为k当x=h时,y有最大值为k
通过填表、画图等活动,在帮助学生获取感性材料的同时,促使他们积极思考、探索、发现规律,揭示结论。 对于函数间的关系,可先由学生猜测,培养学生的合情推理能力和分析能力,再画图验证,亲身经历探索函数性质的过程。
3.学以致用,应用新知 考点 二次函数的图象与性质 P38随堂练习 变式训练 y=a(x﹣h)2+k的图象可以看成y=ax2的图象先沿x轴整体左(右)平移 个单位: 当h>O时,向 平移; 当h<0时,向 平移.再沿对称轴整体上(下)平移 个单位:当k>O时,向 平移; 当k<0时,向下平移.因此,二次函数y=a(x﹣h)2+k的图象是一条抛物线,它的开口方向由 值决定,对称轴为 ,顶点坐标为 。 答案:右 左 |k| 上a 直线x=h (h,k) 在知识梳理的基础上,通过及时的练习,进一步提升学生对二次函数的图象与性质的理解掌握,同时教师可根据学生的掌握情况及时讲解。
4.随堂训练,巩固新知 1. 关于抛物线y=(x﹣1)2﹣2,下列说法错误的是( ) A.开口方向向上 B.对称轴是直线x=1 C.顶点坐标为(﹣1,﹣2) D.当x>1时,y随x的增大而增大 答案:C 2. 如图,已知二次函数y=(x+1)2﹣4,当﹣2≤x≤2时,则函数y的最小值和最大值( ) A.﹣3和5 B.﹣4和5 C.﹣4和﹣3 D.﹣1和5 答案:B 3.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=3(x+1)2+4m(m为常数)上的三点,则y1,y2,y3的大小关系为( ) A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y3<y2<y1 答案:A 4.点A(m﹣1,y1),B(m,y2)都在二次函数y=(x﹣1)2+n的图象上.若y1<y2,则m的取值范围为( ) A.m>2 B.m C.m<1 D.m<2 答案:B 5.小嘉说:将二次函数y=x2的图象平移或翻折后经过点(2,0)有4种方法: ①向右平移2个单位长度 ②向右平移1个单位长度,再向下平移1个单位长度 ③向下平移4个单位长度 ④沿x轴翻折,再向上平移4个单位长度 你认为小嘉说的方法中正确的个数有( ) A.1个 B.2个 C.3个 D.4个 答案:D 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 二次函数y=a(x-h)2和y=a(x-h)2+k图象的性质; 二次函数y=ax2,y=a(x-h)2,y=a(x-h)2+k图象之间的关系。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:P39 习题2.4。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 二次函数的图象与性质(第3课时)二次函数y=a(x-h)2 二次函数y=a(x-h)2+k 平移教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课采用教师引导,学生自主探索和小组合作相结合的教学方式。本课时还课堂于学生,在开放的前提下,让学生经历动手画图、合作交流的过程,给学生一个充分发表见解的舞台,激发学生的创新精神,提高学生的自信力,打造高效课堂! 在学生的探究过程中,教师要注意引导学生进行图象和图象之间的比较、表达式和表达式之间的比较,建立图象和表达式之间的联系, 是否理解表达式的变化将引起图象的何种变化,或者图象的变化将要引起表达式的何种变化。 要引导学生从感性认识上升到理性认识。 反思,更进一步提升。
