2.5.1 二次函数与一元二次方程 教学设计(表格式)北师大版数学九年级下册
文档属性
| 名称 | 2.5.1 二次函数与一元二次方程 教学设计(表格式)北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 310.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 00:00:00 | ||
图片预览



文档简介
4 二次函数与一元二次方程(第1课时)
课题 二次函数与一元二次方程(第1课时) 授课类型 新授课
授课人
教学内容 课本P51-52
教学目标 1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。 2.理解二次函数的图象和横轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不相等的实数根、两个相等的实数根和没有实数根。 3.理解一元二次方程的根就是二次函数的图象与直线y = h(h是实数)交点的横坐标。
教学重难点 重点:理解二次函数y=ax2+bx+c的图象与x轴交点的个数与一元二次方程ax2+bx+c=0的根的个数之间的关系。 难点:理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h交点的横坐标。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情境,导入新课 我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以近似地用公式h=-5t2+v0t+h0表示, 其中h0(m) 是抛出时的高度, v0(m/s)是抛出时的速度。一个小球从地面以40 m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t (s)的关系如图所示。(多媒体呈现) 师生活动:教师提出问题,学生思考交流回答,教师总结引出课题。 教师:同学们,本题中h与t的关系式是什么? 学生:h与t的关系式是h=﹣5t2+40t。 教师:那么小球经过多少秒后落地 学生:通过图象可以看出,小球经过8 s后落地。 教师:还有其他方法可以判断小球落地时间吗? 学生:因为小球落地时,h=0,所以0=﹣5t2+40t,解得t1=0,t2=8,所以小球经过8 s后落地。 教师:同学们,根据图象判断和解方程,得到的结论是否相同? 学生:相同。 教师:是的,我们可以发现,二次函数h=﹣5t2+40t的图象与x轴交点的横坐标与方程0=﹣5t2+40t的根是相同的,那么方程的根与函数之间还有哪些关系呢?今天这节课,我们就一块儿探究下二次函数与一元二次方程的关系。(板书课题:二次函数与一元二次方程 第1课时) 根据小球竖直上抛运动创设情境,有助于提升学生学习的兴趣,同时使学生初步感受二次函数与一元二次方程之间的关系。最后通过师生互动,引出课题。
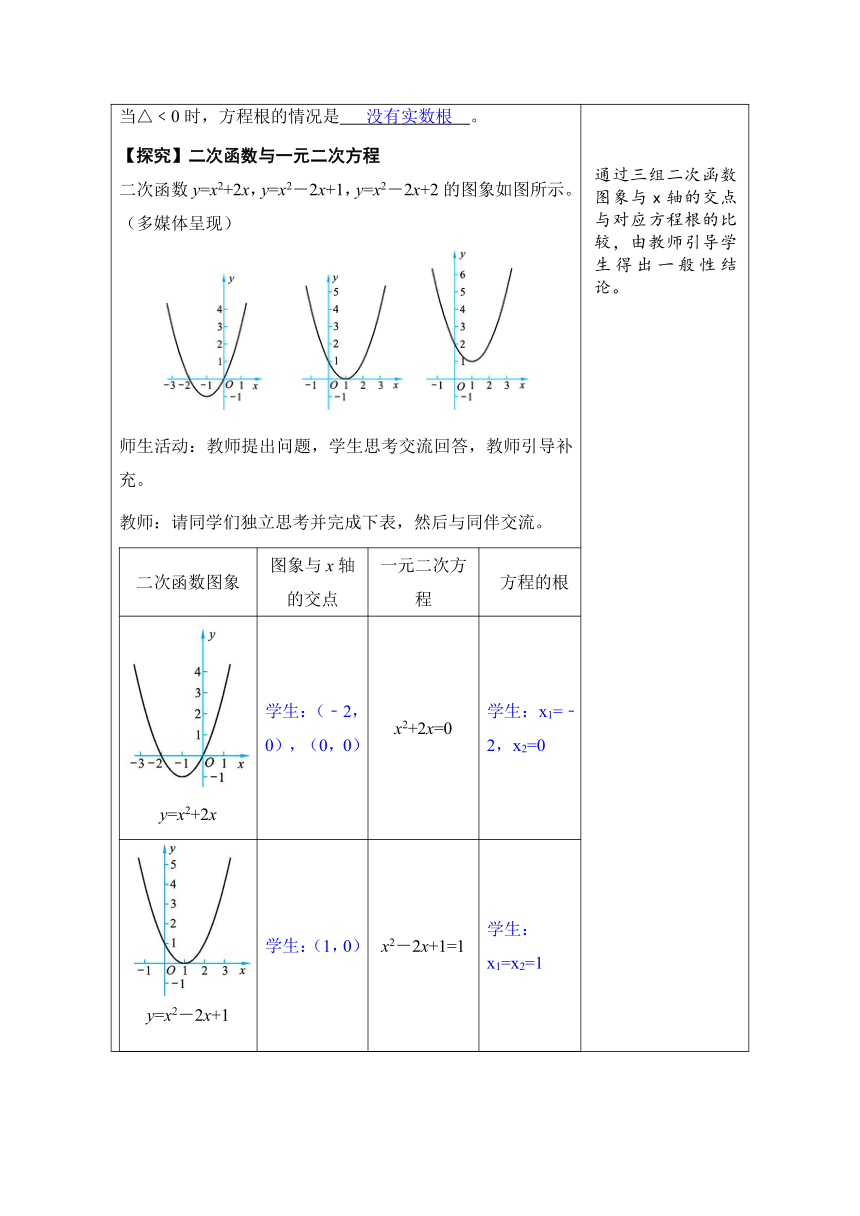
2.实践探究,学习新知 【复习回顾】一元二次方程根与系数的关系 师生活动:教师提出问题,学生思考回答。 教师:同学们还记得一元二次方程根的判别式以及根与系数的关系吗,请回答下面问题。 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。 当△﹥0时,方程根的情况是 ; 当△=0时,方程根的情况是 ; 当△﹤0时,方程根的情况是 。(多媒体呈现) 学生:一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = b2-4ac 。 当△﹥0时,方程根的情况是 有两个不相等的实数根 ; 当△=0时,方程根的情况是 有两个相等的实数根 ; 当△﹤0时,方程根的情况是 没有实数根 。 【探究】二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示。(多媒体呈现) 师生活动:教师提出问题,学生思考交流回答,教师引导补充。 教师:请同学们独立思考并完成下表,然后与同伴交流。 二次函数图象图象与x轴的交点一元二次方程方程的根 y=x2+2x学生:(﹣2,0),(0,0)x2+2x=0学生:x1=﹣2,x2=0 y=x2-2x+1学生:(1,0)x2-2x+1=1学生:x1=x2=1 y=x2-2x+2学生:函数图象与x轴没有交点x2-2x+2=0学生:方程没有实数根
(多媒体呈现) 教师:那么,同学们,思考一下,二次函数y=ax2+bx+c的图象与x轴交点的个数与一元二次方程ax2+bx+c=0的根的个数有什么关系? 学生: 二次函数y=ax2+bx+c的图象与x轴的交点个数一元二次方程ax2+bx+c=0的根的个数有两个交点有两个不相等的实数根有一个交点有两个相等的实数根没有交点没有实数根
教师追问:那么我们是不是可以通过二次函数对应方程的根的判别式来判断二次函数图象与x轴的交点个数? 学生:可以。 教师:进一步思考,二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系? 学生:二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根。 教师:在本节一开始的小球上抛问题中,能否知道小球离地面的高度是60 m时的时间?说说你的方法。 学生:令h=60,则﹣5t2+40t=60,解得t1=2,t2=6。所以第2 s和第6 s时,小球的高度是60 m。 教师:还有其他方法吗? 学生:过点(0,60)作一条与y轴垂直的直线,找到它与抛物线的交点,再分别过交点作x轴的垂线,发现两个垂足的横坐标分别是2,6。所以所以第2 s和第6 s时,小球的高度是60 m。 教师:也就是说直线y=60与二次函数h=﹣5t2+40t的图象的交点的横坐标与方程﹣5t2+40t=60的根是一样的,那么,同学们,猜想下,直线y=h与抛物线y=ax2+bx+c的交点的横坐标与方程h=ax2+bx+c的根有什么关系?为什么? 学生:相同。因为要求交点的横坐标,就是将直线y=h与抛物线y=ax2+bx+c的表达式联立,所得方程就是h=ax2+bx+c,所以直线y=h与抛物线y=ax2+bx+c的交点的横坐标与方程h=ax2+bx+c的根一定是相同的。 【归纳总结】 教师:通过以上的探究学习,我们发现二次函数与一元二次方程之间有什么关系? 学生:①二次函数y=ax2+bx+c的图象与x轴交点的交点个数与一元二次方程ax2+bx+c=0的根的个数一致; ②二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根相同; ③二次函数y=ax2+bx+c的图象与直线y=h的交点个数与一元二次方程ax2+bx+c=h的根的个数一致; ④二次函数y=ax2+bx+c的图象与直线y=h的交点的横坐标与一元二次方程ax2+bx+c=h的根相同。 复习一元二次方程根与系数的关系,为接下来探究函数与方程的关系做铺垫。
3.学以致用,应用新知 考点 二次函数与一元二次方程 P52 随堂练习 【变式训练】 抛物线y=3x2+4x+2与x轴的交点个数是 . 答案:0 已知二次函数y=﹣x2+bx+c的顶点为(1,5),那么关于x的一元二次方程﹣x2+bx+c﹣m=0有两个相等的实数根,则m= . 答案:5 3.若关于x的一元二次方程x2﹣4x+3=m有实数根x1、x2,且x1≠x2,有下列结论: ①m<﹣2; ②x1=1,x2=3; ③二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(1,0)和(3,0). 其中,正确结论的个数是( ) A.0 B.1 C.2 D.3 答案:B 学以致用,通过及时练习,进一步提升学生对新知的理解与运用。
4.随堂训练,巩固新知 1.已知函数y=mx2+3mx+m﹣1的图象与坐标轴恰有两个公共点,则实数m的值为( ) A.m=0或 B. C.m=1或 D.m=1或m=0 答案:C 2.已知抛物线y=ax2+4ax﹣8与直线y=n相交于A,B两点(点A在点B左侧),AB=4,且抛物线与x轴只有一个交点,则n的值为( ) A.﹣8 B.﹣4 C.4 D.8 答案:A 3.已知抛物线y=a(x+1)(x﹣3)﹣4(a≠0)与x轴交点的横坐标为m,n,且m<n,点(x0,y0)是抛物线上一点,则下列结论正确的是( ) A.若a>0,则﹣1<m<n<3 B.当x=m+n 时,y=﹣4 C.方程a(x﹣m)(x﹣n)﹣4=0的解为x1=﹣1,x2=3 D.若a>0,当﹣1<x0<3时,则y0<﹣4 4.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y=|x2+bx+c|的图象如图所示,则下列结论正确的是( ) A.bc<0 B.c=3 C.当直线y=x+m与该图象恰有三个公共点时,则m=1 D.关于x的方程|x2+bx+c|=3的所有实数根的和为4 5. 已知关于x的抛物线y=x2﹣2x+m2+4,其中m为实数. 求证:该抛物线与x轴没有交点。 证明:令y=0,即 x2﹣2x+m2+4=0, ∵Δ=(﹣2)2﹣4(m2+4)=﹣4m2﹣12<0, ∴这条抛物线与x轴没有交点。 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系。 理解了一元二次方程ax2+bx+c=0的根就是二次函数y=ax2+bx+c图象与x轴交点的横坐标。 理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h交点的横坐标。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:P52 习题2.10。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 二次函数与一元二次方程(第1课时)二次函数与一元二次方程教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课以小球竖直上抛为切入点,引出函数与方程的关系,学生通过三组对二次函数图象与x轴的交点与一元二次方程根的对比,探讨得出一元二次方程ax2+bx+c=0的根与二次函数y=ax2+bx+c图象与x轴交点的关系,进而在教师的引导下,拓展得出一元二次方程ax2+bx+c=h的根与二次函数y=ax2+bx+c的图象与直线y=h交点的关系。整节课以学生为主体,教师适当引导,层层推进,使学生充分参与到课堂中来,同时也达成了预期的教学目标。 反思,更进一步提升。
课题 二次函数与一元二次方程(第1课时) 授课类型 新授课
授课人
教学内容 课本P51-52
教学目标 1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系。 2.理解二次函数的图象和横轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不相等的实数根、两个相等的实数根和没有实数根。 3.理解一元二次方程的根就是二次函数的图象与直线y = h(h是实数)交点的横坐标。
教学重难点 重点:理解二次函数y=ax2+bx+c的图象与x轴交点的个数与一元二次方程ax2+bx+c=0的根的个数之间的关系。 难点:理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h交点的横坐标。
教学准备 多媒体课件。
教与学互动设计(教学过程) 设计意图
1.创设情境,导入新课 我们已经知道,竖直上抛物体的高度h(m)与运动时间t(s)的关系可以近似地用公式h=-5t2+v0t+h0表示, 其中h0(m) 是抛出时的高度, v0(m/s)是抛出时的速度。一个小球从地面以40 m/s的速度竖直向上抛起,小球距离地面的高度h(m)与运动时间t (s)的关系如图所示。(多媒体呈现) 师生活动:教师提出问题,学生思考交流回答,教师总结引出课题。 教师:同学们,本题中h与t的关系式是什么? 学生:h与t的关系式是h=﹣5t2+40t。 教师:那么小球经过多少秒后落地 学生:通过图象可以看出,小球经过8 s后落地。 教师:还有其他方法可以判断小球落地时间吗? 学生:因为小球落地时,h=0,所以0=﹣5t2+40t,解得t1=0,t2=8,所以小球经过8 s后落地。 教师:同学们,根据图象判断和解方程,得到的结论是否相同? 学生:相同。 教师:是的,我们可以发现,二次函数h=﹣5t2+40t的图象与x轴交点的横坐标与方程0=﹣5t2+40t的根是相同的,那么方程的根与函数之间还有哪些关系呢?今天这节课,我们就一块儿探究下二次函数与一元二次方程的关系。(板书课题:二次函数与一元二次方程 第1课时) 根据小球竖直上抛运动创设情境,有助于提升学生学习的兴趣,同时使学生初步感受二次函数与一元二次方程之间的关系。最后通过师生互动,引出课题。
2.实践探究,学习新知 【复习回顾】一元二次方程根与系数的关系 师生活动:教师提出问题,学生思考回答。 教师:同学们还记得一元二次方程根的判别式以及根与系数的关系吗,请回答下面问题。 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。 当△﹥0时,方程根的情况是 ; 当△=0时,方程根的情况是 ; 当△﹤0时,方程根的情况是 。(多媒体呈现) 学生:一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = b2-4ac 。 当△﹥0时,方程根的情况是 有两个不相等的实数根 ; 当△=0时,方程根的情况是 有两个相等的实数根 ; 当△﹤0时,方程根的情况是 没有实数根 。 【探究】二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示。(多媒体呈现) 师生活动:教师提出问题,学生思考交流回答,教师引导补充。 教师:请同学们独立思考并完成下表,然后与同伴交流。 二次函数图象图象与x轴的交点一元二次方程方程的根 y=x2+2x学生:(﹣2,0),(0,0)x2+2x=0学生:x1=﹣2,x2=0 y=x2-2x+1学生:(1,0)x2-2x+1=1学生:x1=x2=1 y=x2-2x+2学生:函数图象与x轴没有交点x2-2x+2=0学生:方程没有实数根
(多媒体呈现) 教师:那么,同学们,思考一下,二次函数y=ax2+bx+c的图象与x轴交点的个数与一元二次方程ax2+bx+c=0的根的个数有什么关系? 学生: 二次函数y=ax2+bx+c的图象与x轴的交点个数一元二次方程ax2+bx+c=0的根的个数有两个交点有两个不相等的实数根有一个交点有两个相等的实数根没有交点没有实数根
教师追问:那么我们是不是可以通过二次函数对应方程的根的判别式来判断二次函数图象与x轴的交点个数? 学生:可以。 教师:进一步思考,二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系? 学生:二次函数y=ax2+bx+c的图象与x轴交点的横坐标就是一元二次方程ax2+bx+c=0的根。 教师:在本节一开始的小球上抛问题中,能否知道小球离地面的高度是60 m时的时间?说说你的方法。 学生:令h=60,则﹣5t2+40t=60,解得t1=2,t2=6。所以第2 s和第6 s时,小球的高度是60 m。 教师:还有其他方法吗? 学生:过点(0,60)作一条与y轴垂直的直线,找到它与抛物线的交点,再分别过交点作x轴的垂线,发现两个垂足的横坐标分别是2,6。所以所以第2 s和第6 s时,小球的高度是60 m。 教师:也就是说直线y=60与二次函数h=﹣5t2+40t的图象的交点的横坐标与方程﹣5t2+40t=60的根是一样的,那么,同学们,猜想下,直线y=h与抛物线y=ax2+bx+c的交点的横坐标与方程h=ax2+bx+c的根有什么关系?为什么? 学生:相同。因为要求交点的横坐标,就是将直线y=h与抛物线y=ax2+bx+c的表达式联立,所得方程就是h=ax2+bx+c,所以直线y=h与抛物线y=ax2+bx+c的交点的横坐标与方程h=ax2+bx+c的根一定是相同的。 【归纳总结】 教师:通过以上的探究学习,我们发现二次函数与一元二次方程之间有什么关系? 学生:①二次函数y=ax2+bx+c的图象与x轴交点的交点个数与一元二次方程ax2+bx+c=0的根的个数一致; ②二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根相同; ③二次函数y=ax2+bx+c的图象与直线y=h的交点个数与一元二次方程ax2+bx+c=h的根的个数一致; ④二次函数y=ax2+bx+c的图象与直线y=h的交点的横坐标与一元二次方程ax2+bx+c=h的根相同。 复习一元二次方程根与系数的关系,为接下来探究函数与方程的关系做铺垫。
3.学以致用,应用新知 考点 二次函数与一元二次方程 P52 随堂练习 【变式训练】 抛物线y=3x2+4x+2与x轴的交点个数是 . 答案:0 已知二次函数y=﹣x2+bx+c的顶点为(1,5),那么关于x的一元二次方程﹣x2+bx+c﹣m=0有两个相等的实数根,则m= . 答案:5 3.若关于x的一元二次方程x2﹣4x+3=m有实数根x1、x2,且x1≠x2,有下列结论: ①m<﹣2; ②x1=1,x2=3; ③二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(1,0)和(3,0). 其中,正确结论的个数是( ) A.0 B.1 C.2 D.3 答案:B 学以致用,通过及时练习,进一步提升学生对新知的理解与运用。
4.随堂训练,巩固新知 1.已知函数y=mx2+3mx+m﹣1的图象与坐标轴恰有两个公共点,则实数m的值为( ) A.m=0或 B. C.m=1或 D.m=1或m=0 答案:C 2.已知抛物线y=ax2+4ax﹣8与直线y=n相交于A,B两点(点A在点B左侧),AB=4,且抛物线与x轴只有一个交点,则n的值为( ) A.﹣8 B.﹣4 C.4 D.8 答案:A 3.已知抛物线y=a(x+1)(x﹣3)﹣4(a≠0)与x轴交点的横坐标为m,n,且m<n,点(x0,y0)是抛物线上一点,则下列结论正确的是( ) A.若a>0,则﹣1<m<n<3 B.当x=m+n 时,y=﹣4 C.方程a(x﹣m)(x﹣n)﹣4=0的解为x1=﹣1,x2=3 D.若a>0,当﹣1<x0<3时,则y0<﹣4 4.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y=|x2+bx+c|的图象如图所示,则下列结论正确的是( ) A.bc<0 B.c=3 C.当直线y=x+m与该图象恰有三个公共点时,则m=1 D.关于x的方程|x2+bx+c|=3的所有实数根的和为4 5. 已知关于x的抛物线y=x2﹣2x+m2+4,其中m为实数. 求证:该抛物线与x轴没有交点。 证明:令y=0,即 x2﹣2x+m2+4=0, ∵Δ=(﹣2)2﹣4(m2+4)=﹣4m2﹣12<0, ∴这条抛物线与x轴没有交点。 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系。 理解了一元二次方程ax2+bx+c=0的根就是二次函数y=ax2+bx+c图象与x轴交点的横坐标。 理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c 与直线y=h交点的横坐标。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:P52 习题2.10。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 二次函数与一元二次方程(第1课时)二次函数与一元二次方程教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课以小球竖直上抛为切入点,引出函数与方程的关系,学生通过三组对二次函数图象与x轴的交点与一元二次方程根的对比,探讨得出一元二次方程ax2+bx+c=0的根与二次函数y=ax2+bx+c图象与x轴交点的关系,进而在教师的引导下,拓展得出一元二次方程ax2+bx+c=h的根与二次函数y=ax2+bx+c的图象与直线y=h交点的关系。整节课以学生为主体,教师适当引导,层层推进,使学生充分参与到课堂中来,同时也达成了预期的教学目标。 反思,更进一步提升。
