3.6.1 直线和圆位置关系 教学设计(表格式)北师大版数学九年级下册
文档属性
| 名称 | 3.6.1 直线和圆位置关系 教学设计(表格式)北师大版数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 522.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 22:01:55 | ||
图片预览


文档简介
6 直线和圆的位置关系 (第1课时)
课题 直线和圆的位置关系 (第1课时) 授课类型 新授课
授课人
教学内容 课本P89-91
教学目标 经历探索直线与圆的位置关系的过程,了解直线与圆有相交、相切、相离三种位置关系。 掌握切线的概念;探索切线与过切点的半径之间的关系。
教学重难点 重点:理解直线与圆的三种位置关系的定义,并能准确的判定。 难点:利用d与r的大小关系判断直线与圆的位置关系;运用切线的性质定理解决问题。
教学准备 多媒体课件,圆规,直尺,三角尺。
教与学互动设计(教学过程) 设计意图
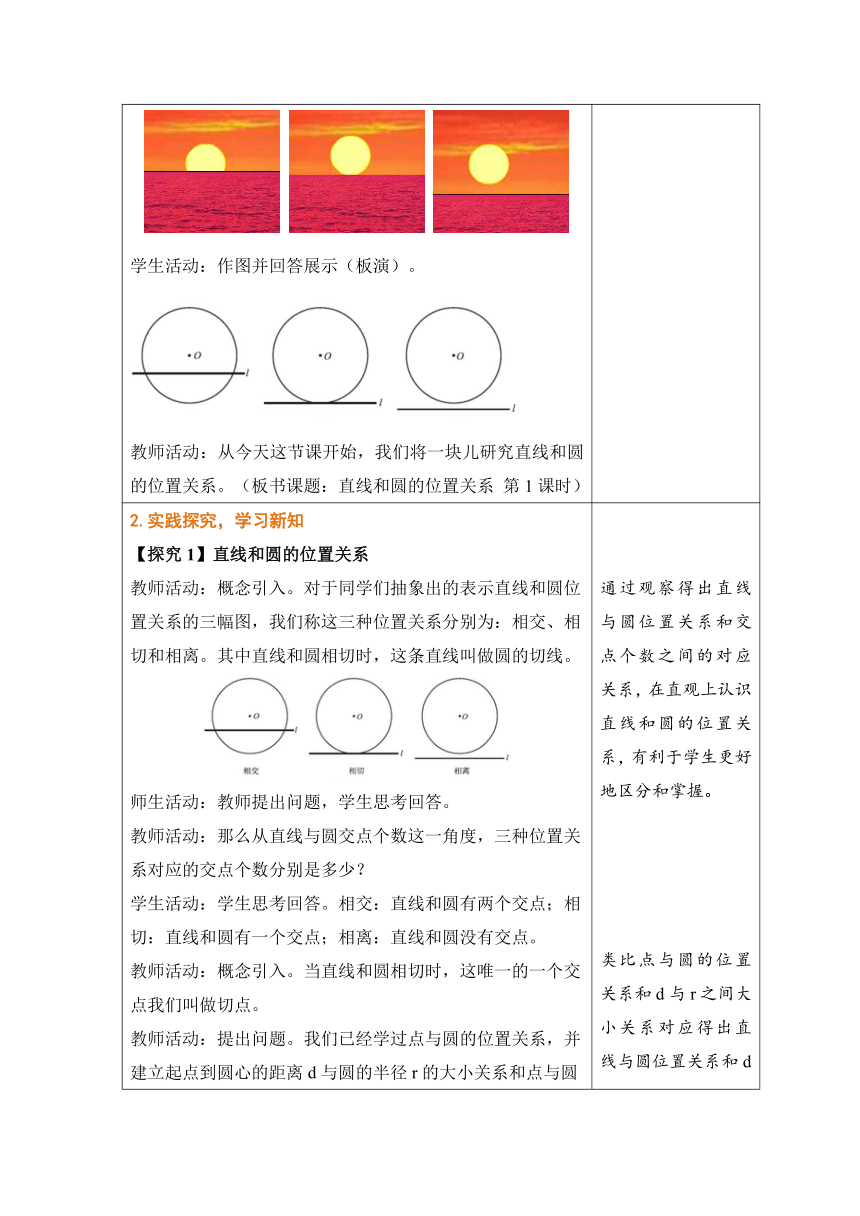
1.创设情境,导入新课 欣赏《海上日出》的视频,感受生活中反映直线与圆的位置关系的现象(多媒体呈现) 师生活动:教师提出问题,学生回答,教师引出课题。 教师活动:从刚才的视频中,我们发现地平线与太阳的位置关系是怎样的? 学生活动:直接回答。没有完全露出海面,刚好露出水面以及最后完全离开海面。 教师活动:展示三种情况的图片并提问。是的,那同学们能把从中抽象出的直线和圆的位置关系画出来吗? 学生活动:作图并回答展示(板演)。 教师活动:从今天这节课开始,我们将一块儿研究直线和圆的位置关系。(板书课题:直线和圆的位置关系 第1课时) 以大气磅礴的海上日出为背景,创设情境,渗透数学与生活息息相关的思想,容易调动学生的积极性,引导学生用数学的眼光观察日出,在学生观察思考后,引出本节课课题。
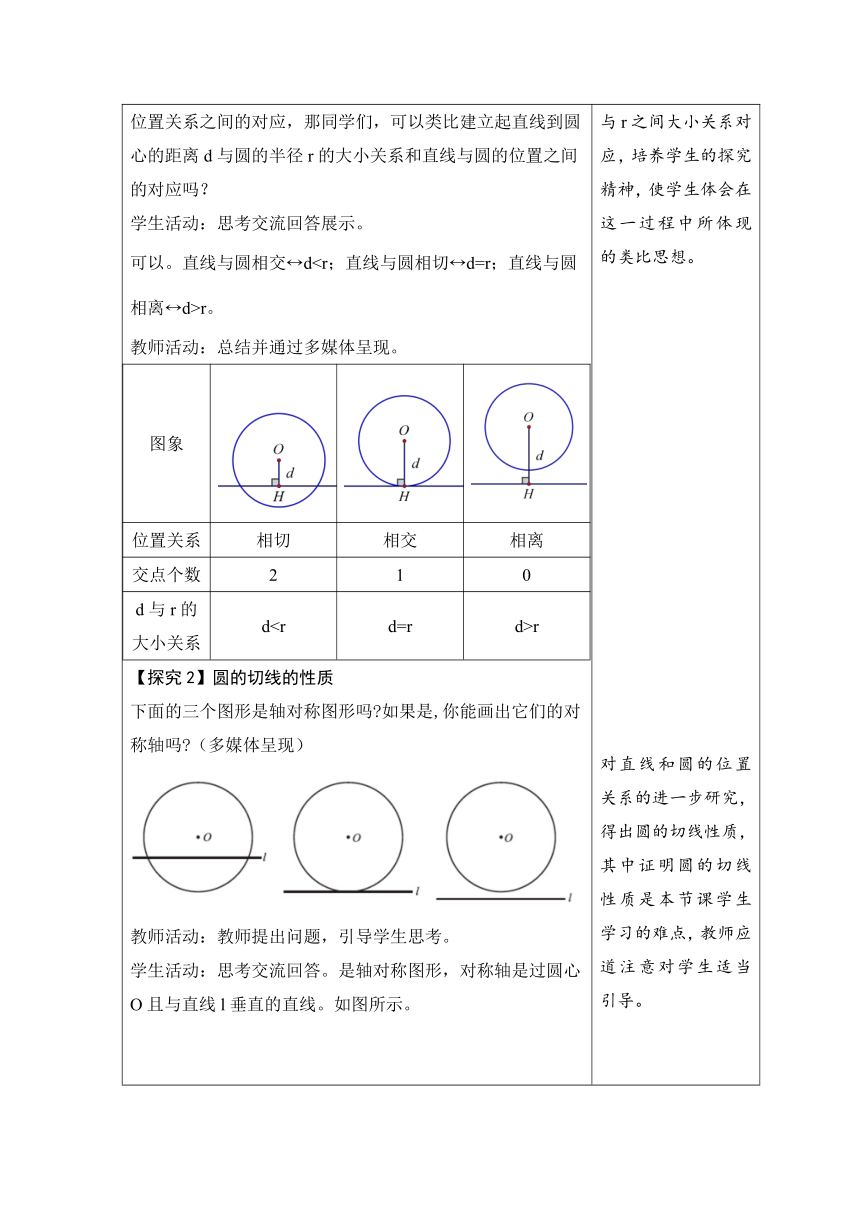
2.实践探究,学习新知 【探究1】直线和圆的位置关系 教师活动:概念引入。对于同学们抽象出的表示直线和圆位置关系的三幅图,我们称这三种位置关系分别为:相交、相切和相离。其中直线和圆相切时,这条直线叫做圆的切线。 师生活动:教师提出问题,学生思考回答。 教师活动:那么从直线与圆交点个数这一角度,三种位置关系对应的交点个数分别是多少? 学生活动:学生思考回答。相交:直线和圆有两个交点;相切:直线和圆有一个交点;相离:直线和圆没有交点。 教师活动:概念引入。当直线和圆相切时,这唯一的一个交点我们叫做切点。 教师活动:提出问题。我们已经学过点与圆的位置关系,并建立起点到圆心的距离d与圆的半径r的大小关系和点与圆位置关系之间的对应,那同学们,可以类比建立起直线到圆心的距离d与圆的半径r的大小关系和直线与圆的位置之间的对应吗? 学生活动:思考交流回答展示。 可以。直线与圆相交 dr。 教师活动:总结并通过多媒体呈现。 图象位置关系相切相交相离交点个数210d与r的大小关系dr
【探究2】圆的切线的性质 下面的三个图形是轴对称图形吗 如果是,你能画出它们的对称轴吗 (多媒体呈现) 教师活动:教师提出问题,引导学生思考。 学生活动:思考交流回答。是轴对称图形,对称轴是过圆心O且与直线l垂直的直线。如图所示。 教师活动:提出问题,引导学生思考。如图,如果已知直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说一说你的理由。(多媒体呈现) 学生活动:思考交流讨论回答。 AB⊥CD。理由:因为是轴对称图形,AB所在的直线是对称轴,所以沿AB对折图形时,AC与AD重合,因此∠BAC =∠BAD = 90°。 教师活动:介绍反正法,并引入切线性质。 AB与CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD(如图),垂足为M,则OM < OA,即圆心O到直线CD的距离小于⊙O的半径,因此CD与⊙O相交。这与已知条件“直线CD与⊙O相切”相矛盾,所以AB与CD垂直。 圆的切线的性质:圆的切线垂直于过切点的半径。(板书或多媒体呈现) 例 已知 Rt△ABC的斜边AB=8 cm, AC =4 cm。 (1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切? (2)以点C为圆心,分别以2 cm和4 cm 的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?(多媒体呈现) 师生活动:学生思考回答,学生代表板演,教师规范解题步骤。 学生:(1)如图,过点C作AB的垂线,垂足为D。 ∵AC=4 cm,AB=8 cm, ∴cos A==。 ∴∠A=60°。 ∴CD=ACsin A=4sin 60°=2(cm)。 (2)由(1)可知,圆心C到AB的距离d=2 cm,所以 当r=2 cm时,d>r,⊙C与AB相离; 当r=4 cm时,d3.学以致用,应用新知 考点1 直线与圆的位置关系 随堂练习 1 变式训练 如图,以点O为圆心作圆,所得的圆与直线a相切的是( ) A.以OA为半径的圆 B.以OB为半径的圆 C.以OC为半径的圆 D.以OD为半径的圆 答案:D 考点2 圆的切线的性质 随堂练习 1 变式训练 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( ) A.25° B.35° C.40° D.50 答案:C 学以致用,通过及时练习,进一步提升学生对新知的理解与运用。
4.随堂训练,巩固新知 1. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( ) A.相切 B.相交 C.相离 D.平行 答案:B 2. 在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆与坐标轴的位置关系为( ) A.与x轴相离、与y轴相切 B.与x轴、y轴都相离 C.与x轴相切、y轴相离 D.与x轴、y轴都相切 答案:B 3. 如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( ) A. B. C. D. 答案:C 4. 如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内、使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,则点E在量角器上所对应的锐角度数是( ) A.60° B.45° C.75° D.50° 答案:A 5. 如图,一圆环分别与夹角为α的两墙面相切,圆环上图示位置固定一小球,并用细线将小球与两切点分别相连,两细线夹角为β,则α与β之间的关系是( ) A. B. β=90°+α C. D.β=180°﹣α 答案:A 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 经历探索直线与圆的位置关系的过程,了解直线与圆有相交、相切、相离三种位置关系。 掌握切线的概念以及切线与过切点的半径之间的关系。 能够利用d与r的大小关系判断直线与圆的位置关系。 能够运用切线的性质定理解决问题。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:习题3.7。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 直线和圆的位置关系(第1课时)直线和圆的位置关系 圆的切线的性质教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课由海上日出的情景,引发学生学习的热情,从而使学生能够积极地投身到课堂的探究活动中。同时本节课采用多媒体进行教学,发挥其直观、形象等效果,力求使教学内容情境化、生活化、问题化,力争深入浅出,提高教学效率。同时本节课的教学策略主要是通过教师引导,让学生通过观察、思考、交流等合作活动亲身经历知识的发生、发展及其探求过程,同时培养学生类比的思维方法以及数形结合的思想。整体而言,本节课充分将课堂还给学生,以学生为主体,进而把数学的课堂变成数学探讨的课堂,学生探究的课堂。 反思,更进一步提升。
课题 直线和圆的位置关系 (第1课时) 授课类型 新授课
授课人
教学内容 课本P89-91
教学目标 经历探索直线与圆的位置关系的过程,了解直线与圆有相交、相切、相离三种位置关系。 掌握切线的概念;探索切线与过切点的半径之间的关系。
教学重难点 重点:理解直线与圆的三种位置关系的定义,并能准确的判定。 难点:利用d与r的大小关系判断直线与圆的位置关系;运用切线的性质定理解决问题。
教学准备 多媒体课件,圆规,直尺,三角尺。
教与学互动设计(教学过程) 设计意图
1.创设情境,导入新课 欣赏《海上日出》的视频,感受生活中反映直线与圆的位置关系的现象(多媒体呈现) 师生活动:教师提出问题,学生回答,教师引出课题。 教师活动:从刚才的视频中,我们发现地平线与太阳的位置关系是怎样的? 学生活动:直接回答。没有完全露出海面,刚好露出水面以及最后完全离开海面。 教师活动:展示三种情况的图片并提问。是的,那同学们能把从中抽象出的直线和圆的位置关系画出来吗? 学生活动:作图并回答展示(板演)。 教师活动:从今天这节课开始,我们将一块儿研究直线和圆的位置关系。(板书课题:直线和圆的位置关系 第1课时) 以大气磅礴的海上日出为背景,创设情境,渗透数学与生活息息相关的思想,容易调动学生的积极性,引导学生用数学的眼光观察日出,在学生观察思考后,引出本节课课题。
2.实践探究,学习新知 【探究1】直线和圆的位置关系 教师活动:概念引入。对于同学们抽象出的表示直线和圆位置关系的三幅图,我们称这三种位置关系分别为:相交、相切和相离。其中直线和圆相切时,这条直线叫做圆的切线。 师生活动:教师提出问题,学生思考回答。 教师活动:那么从直线与圆交点个数这一角度,三种位置关系对应的交点个数分别是多少? 学生活动:学生思考回答。相交:直线和圆有两个交点;相切:直线和圆有一个交点;相离:直线和圆没有交点。 教师活动:概念引入。当直线和圆相切时,这唯一的一个交点我们叫做切点。 教师活动:提出问题。我们已经学过点与圆的位置关系,并建立起点到圆心的距离d与圆的半径r的大小关系和点与圆位置关系之间的对应,那同学们,可以类比建立起直线到圆心的距离d与圆的半径r的大小关系和直线与圆的位置之间的对应吗? 学生活动:思考交流回答展示。 可以。直线与圆相交 d
【探究2】圆的切线的性质 下面的三个图形是轴对称图形吗 如果是,你能画出它们的对称轴吗 (多媒体呈现) 教师活动:教师提出问题,引导学生思考。 学生活动:思考交流回答。是轴对称图形,对称轴是过圆心O且与直线l垂直的直线。如图所示。 教师活动:提出问题,引导学生思考。如图,如果已知直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系?说一说你的理由。(多媒体呈现) 学生活动:思考交流讨论回答。 AB⊥CD。理由:因为是轴对称图形,AB所在的直线是对称轴,所以沿AB对折图形时,AC与AD重合,因此∠BAC =∠BAD = 90°。 教师活动:介绍反正法,并引入切线性质。 AB与CD要么垂直,要么不垂直.假设AB与CD不垂直,过点O作一条直径垂直于CD(如图),垂足为M,则OM < OA,即圆心O到直线CD的距离小于⊙O的半径,因此CD与⊙O相交。这与已知条件“直线CD与⊙O相切”相矛盾,所以AB与CD垂直。 圆的切线的性质:圆的切线垂直于过切点的半径。(板书或多媒体呈现) 例 已知 Rt△ABC的斜边AB=8 cm, AC =4 cm。 (1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切? (2)以点C为圆心,分别以2 cm和4 cm 的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?(多媒体呈现) 师生活动:学生思考回答,学生代表板演,教师规范解题步骤。 学生:(1)如图,过点C作AB的垂线,垂足为D。 ∵AC=4 cm,AB=8 cm, ∴cos A==。 ∴∠A=60°。 ∴CD=ACsin A=4sin 60°=2(cm)。 (2)由(1)可知,圆心C到AB的距离d=2 cm,所以 当r=2 cm时,d>r,⊙C与AB相离; 当r=4 cm时,d
4.随堂训练,巩固新知 1. 如图是“光盘行动”的宣传海报,图中餐盘与筷子可看成直线和圆的位置关系是( ) A.相切 B.相交 C.相离 D.平行 答案:B 2. 在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆与坐标轴的位置关系为( ) A.与x轴相离、与y轴相切 B.与x轴、y轴都相离 C.与x轴相切、y轴相离 D.与x轴、y轴都相切 答案:B 3. 如图,⊙O是等边△ABC的外接圆,若AB=3,则⊙O的半径是( ) A. B. C. D. 答案:C 4. 如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内、使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,则点E在量角器上所对应的锐角度数是( ) A.60° B.45° C.75° D.50° 答案:A 5. 如图,一圆环分别与夹角为α的两墙面相切,圆环上图示位置固定一小球,并用细线将小球与两切点分别相连,两细线夹角为β,则α与β之间的关系是( ) A. B. β=90°+α C. D.β=180°﹣α 答案:A 进一步巩固新知,同时为学生提供自我检测的机会,教师也可针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 教师引导学生畅所欲言地谈谈本节课的收获: 经历探索直线与圆的位置关系的过程,了解直线与圆有相交、相切、相离三种位置关系。 掌握切线的概念以及切线与过切点的半径之间的关系。 能够利用d与r的大小关系判断直线与圆的位置关系。 能够运用切线的性质定理解决问题。 通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
6.布置作业 1.书面作业:习题3.7。 让学生所学知识得以运用,在巩固学生知识技能的同时也减轻学生负担。
板书设计 直线和圆的位置关系(第1课时)直线和圆的位置关系 圆的切线的性质教师题目讲解 学生活动区投影区
提纲掣领,重点突出。
教后反思 本节课由海上日出的情景,引发学生学习的热情,从而使学生能够积极地投身到课堂的探究活动中。同时本节课采用多媒体进行教学,发挥其直观、形象等效果,力求使教学内容情境化、生活化、问题化,力争深入浅出,提高教学效率。同时本节课的教学策略主要是通过教师引导,让学生通过观察、思考、交流等合作活动亲身经历知识的发生、发展及其探求过程,同时培养学生类比的思维方法以及数形结合的思想。整体而言,本节课充分将课堂还给学生,以学生为主体,进而把数学的课堂变成数学探讨的课堂,学生探究的课堂。 反思,更进一步提升。
