专题强化练6 折射和全反射在科技、生产、生活中的应用(含答案解析)
文档属性
| 名称 | 专题强化练6 折射和全反射在科技、生产、生活中的应用(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 264.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-23 10:07:42 | ||
图片预览



文档简介
专题强化练6 折射和全反射在科技、生产、生活中的应用
1.如图所示为单反照相机取景器的示意图,五边形ABCDE为五棱镜的一个截面,AB⊥BC。光线垂直于AB边射入,分别在CD和EA上发生反射,且两次入射角相等,最后光线垂直于BC射出。若两次反射均为全反射,则该五棱镜折射率的最小值是 ( )
A.n=
B.n=
C.n=
D.n=
2日晕又叫圆虹,是一种大气光学现象,是日光通过卷层云时,受到冰晶的折射或反射而形成的,如图甲所示。当一束复色光射入卷层云中的冰晶后,经过两次折射,分散成不同方向的单色光,如图乙所示,a、b为其折射出的光中的两束单色光。下列说法正确的是 ( )
A.冰晶对a光的折射率大于对b光的折射率
B.在冰晶中a光的传播速度小于b光的传播速度
C.从冰晶中射入空气界面发生全反射时b光的临界角较小
D.在冰晶中a光的波长小于b光的波长
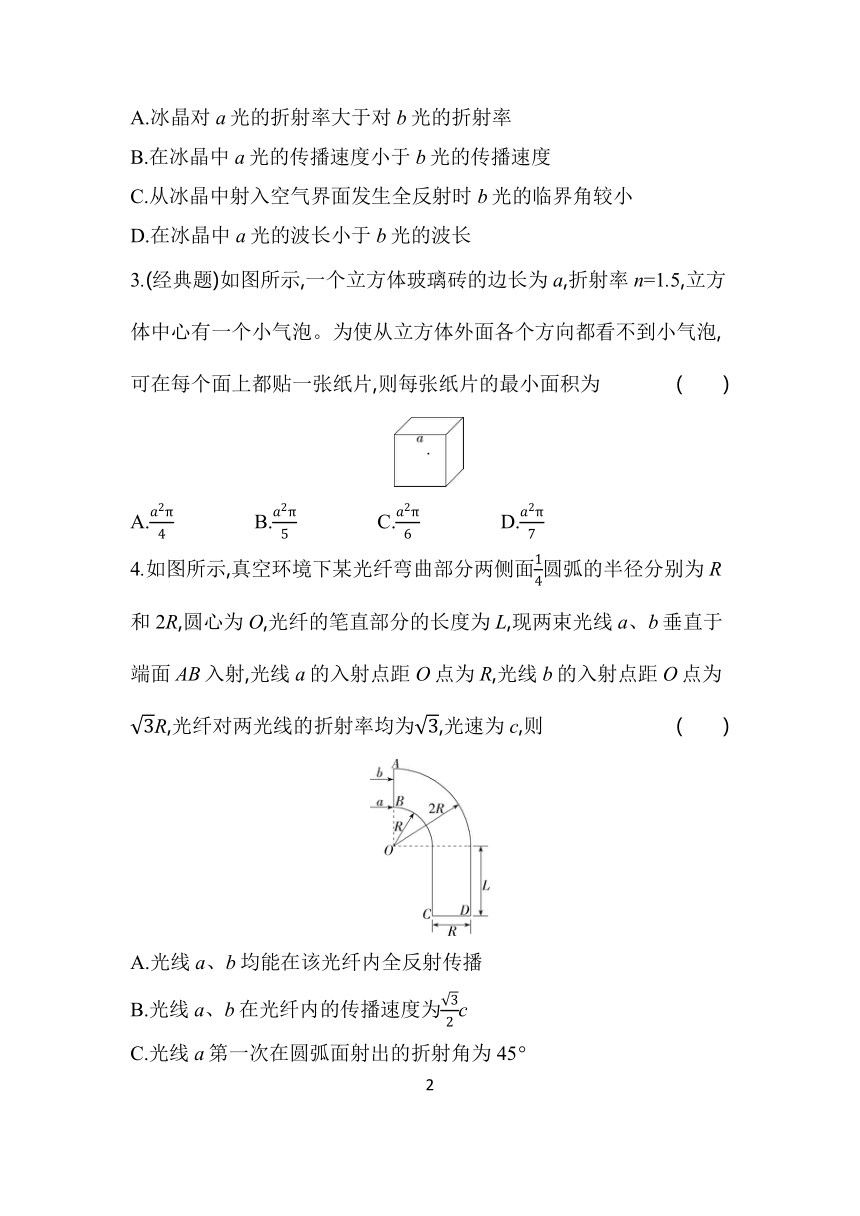
3.(经典题)如图所示,一个立方体玻璃砖的边长为a,折射率n=1.5,立方体中心有一个小气泡。为使从立方体外面各个方向都看不到小气泡,可在每个面上都贴一张纸片,则每张纸片的最小面积为 ( )
A. B. C. D.
4.如图所示,真空环境下某光纤弯曲部分两侧面圆弧的半径分别为R和2R,圆心为O,光纤的笔直部分的长度为L,现两束光线a、b垂直于端面AB入射,光线a的入射点距O点为R,光线b的入射点距O点为R,光纤对两光线的折射率均为,光速为c,则 ( )
A.光线a、b均能在该光纤内全反射传播
B.光线a、b在光纤内的传播速度为c
C.光线a第一次在圆弧面射出的折射角为45°
D.光线b在光纤内传播时间后从CD面射出
5.(经典题)如图所示,有一救生员面向泳池坐在池边的高凳上,他的眼睛到地面的高度为H0=1.8 m,眼睛到池边缘的水平距离为d=2.4 m,当泳池注满水时,水深度可达H1=2.0 m,此时救生员可观察到池底离池边缘最近的点为P,P点到左侧池边缘的水平距离为x1=1.5 m,水池边缘与PO之间的范围为“视线盲区”。
(1)求水的折射率。
(2)若水池并未注满水,水深仅为H2=1.8 m时,求救生员可观察到池底离左侧池边缘的最近点到左侧池边缘的水平距离x2。若水位降低时,该距离是增大还是减小 要减小“视线盲区”,救生员的凳子应该调高些还是矮些 (结果保留3位有效数字)
6.如图甲所示,自行车尾灯在夜晚被灯光照射时特别明亮。尾灯结构可简化成截面为等腰直角三角形的三棱镜,如图乙所示,AB边长为2L,A、D距离为L,一束单色光从D点垂直于AM面入射,恰好在AB面上发生全反射,已知光速为c。求:
(1)三棱镜的折射率;
(2)光在三棱镜中的传播时间。
7.发光二极管(LED)可高效地将电能转化为光能,在照明、平板显示、医疗器件等领域具有广泛的用途。有一种发光二极管,它由透明柱体和发光管芯组成。如图所示为一透明柱体的纵截面,柱体上半部分是球心为O、半径为R的半球体,M是球体的顶点,柱体下半部分是高度为R的圆柱体,其下表面的圆心为D、半径为R,管芯发光区域是半径为r且紧贴柱体下表面的圆面(PQ是直径,圆心也在D点)。
(1)若透明柱体的折射率n0=,真空中光速为c,求光从P点沿直线传播到M点的时间t;
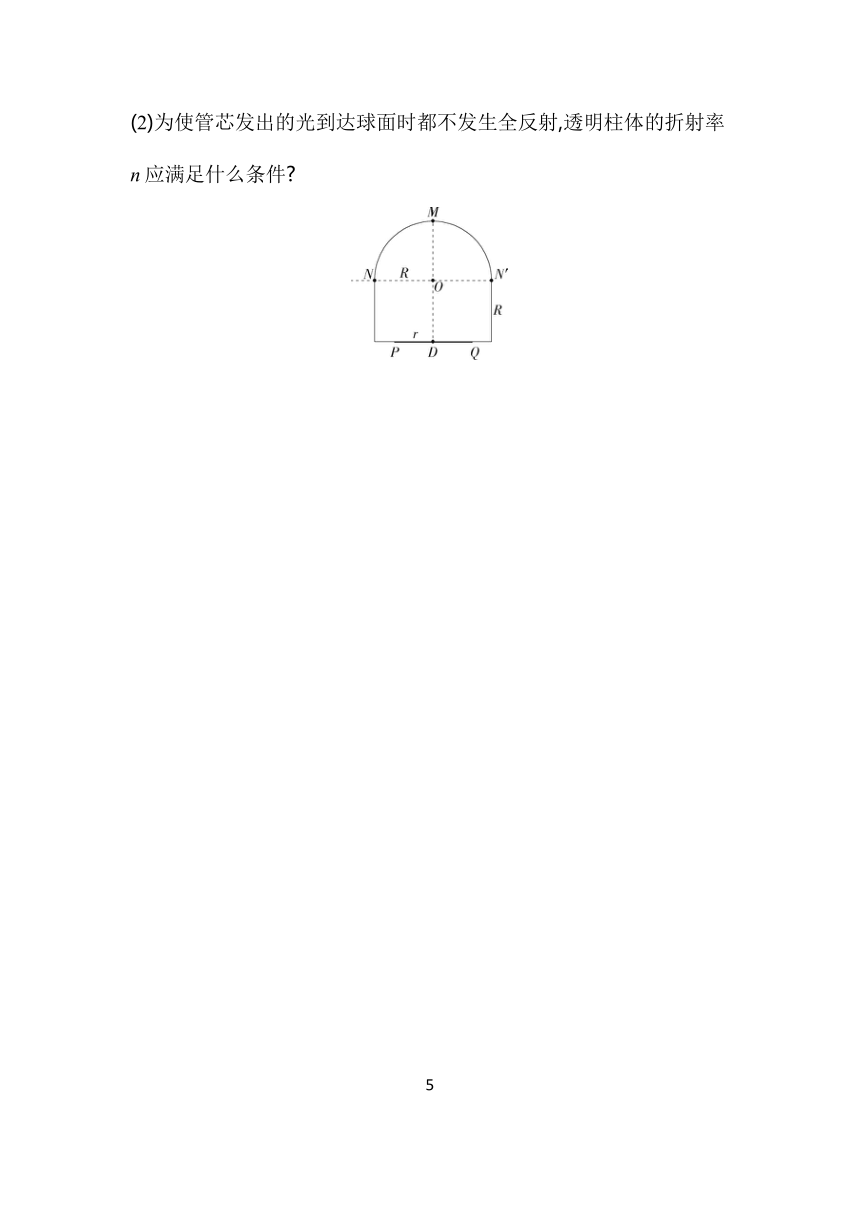
(2)为使管芯发出的光到达球面时都不发生全反射,透明柱体的折射率n应满足什么条件
答案与分层梯度式解析
专题强化练6 折射和全反射在科技、生产、生活中的应用
1.A 设CD面上的入射角为θ,因为在CD和EA上发生全反射,且两次反射的入射角相等,作光路图如图所示。
根据几何关系有4θ=90°。解得θ=22.5°。当光刚好在CD和AE面上发生全反射时,折射率最小,有sin θ=,解得五棱镜的最小折射率为n=,故A正确。
2.C 复色光射入冰晶时,a光的折射角大于b光的折射角,由折射定律可知冰晶对a光的折射率小于对b光的折射率,故a光的频率比b光的频率小;根据v=,可知b光在冰晶中的传播速度较小,故A、B错误;由临界角公式sin C=可知,冰晶对b光的折射率大,故b光从冰晶射向空气时发生全反射的临界角小,C正确;由于v=λf,光在冰晶中的波长λ===λ0,由于a光在真空中的波长大于b光的波长,而冰晶对a光的折射率又小于对b光的,故a光在冰晶中的波长大于b光在冰晶中的波长,故D错误。
3.B 为使从立方体外面各个方向都看不到小气泡,纸片最小时,来自气泡的光恰好在纸片边缘发生全反射,由sin C==,得tan C=。由几何关系可知tan C=,S=πr2,得S=,故B正确。
关键点拨 画出恰好发生全反射时的临界光线,此情景对应的面积为纸片的最小面积。运用折射定律和几何知识求出该半径,从而求出面积即可。
4.D 两束光发生全反射的临界角C满足sin C===,而a、b两束光线第一次到达外侧圆弧的入射角分别满足sin αb==,sin αa==,可知αb>C,αa则b光传播的距离为s=R+2R+,γb=60°,因此传播时间为t==,故D正确。
5.答案 (1) (2)1.62 m 增大 调高些
解析 (1)来自P点的光线在水面发生折射后进入人眼,设入射角为r,折射角为i。由几何关系可知sin i=,sin r=,则水的折射率n=,联立各式代入数据解得n=。
(2)水深仅为H2=1.8 m时,设刚好能看到的最近点为P',来自P'点的光线在水面发生折射进入人眼时入射角和折射角均不变,光路图如图所示。
由几何关系得x2=H2 tan r+(H1-H2)tan i,代入数据解得x2≈1.62 m。
若水位降低时,该距离增大。
要减小“视线盲区”,则救生员的凳子应该调高些。
6.答案 (1) (2)L
解析 (1)光路如图所示。
光线恰好在AB面上发生全反射,则全反射临界角C=∠A=45°,
根据sin C=,解得n=。
(2)根据几何知识得AD=DE=FG=L,
AE==L,BF=BE=AB-AE=L,
则EF===2L,
则光在三棱镜中传播的路程为s=DE+EF+FG=4L,
光在三棱镜中的传播速度v=,
光在三棱镜中的传播时间t=,
解得t=L。
7.答案 (1) (2)n<
解析 (1)光在透明柱体中的传播速度为v=,
P到M点的距离为s=,
解得从P点沿直线传播到M点的时间为t==。
(2)光路图如图所示。
从P点射到N或从Q点射到N'点的光在球面处的入射角最大,设为i,则
sin i=,
设光发生全反射的临界角为C,则
sin C=,
不发生全反射,应满足sin i解得n<。
7
1.如图所示为单反照相机取景器的示意图,五边形ABCDE为五棱镜的一个截面,AB⊥BC。光线垂直于AB边射入,分别在CD和EA上发生反射,且两次入射角相等,最后光线垂直于BC射出。若两次反射均为全反射,则该五棱镜折射率的最小值是 ( )
A.n=
B.n=
C.n=
D.n=
2日晕又叫圆虹,是一种大气光学现象,是日光通过卷层云时,受到冰晶的折射或反射而形成的,如图甲所示。当一束复色光射入卷层云中的冰晶后,经过两次折射,分散成不同方向的单色光,如图乙所示,a、b为其折射出的光中的两束单色光。下列说法正确的是 ( )
A.冰晶对a光的折射率大于对b光的折射率
B.在冰晶中a光的传播速度小于b光的传播速度
C.从冰晶中射入空气界面发生全反射时b光的临界角较小
D.在冰晶中a光的波长小于b光的波长
3.(经典题)如图所示,一个立方体玻璃砖的边长为a,折射率n=1.5,立方体中心有一个小气泡。为使从立方体外面各个方向都看不到小气泡,可在每个面上都贴一张纸片,则每张纸片的最小面积为 ( )
A. B. C. D.
4.如图所示,真空环境下某光纤弯曲部分两侧面圆弧的半径分别为R和2R,圆心为O,光纤的笔直部分的长度为L,现两束光线a、b垂直于端面AB入射,光线a的入射点距O点为R,光线b的入射点距O点为R,光纤对两光线的折射率均为,光速为c,则 ( )
A.光线a、b均能在该光纤内全反射传播
B.光线a、b在光纤内的传播速度为c
C.光线a第一次在圆弧面射出的折射角为45°
D.光线b在光纤内传播时间后从CD面射出
5.(经典题)如图所示,有一救生员面向泳池坐在池边的高凳上,他的眼睛到地面的高度为H0=1.8 m,眼睛到池边缘的水平距离为d=2.4 m,当泳池注满水时,水深度可达H1=2.0 m,此时救生员可观察到池底离池边缘最近的点为P,P点到左侧池边缘的水平距离为x1=1.5 m,水池边缘与PO之间的范围为“视线盲区”。
(1)求水的折射率。
(2)若水池并未注满水,水深仅为H2=1.8 m时,求救生员可观察到池底离左侧池边缘的最近点到左侧池边缘的水平距离x2。若水位降低时,该距离是增大还是减小 要减小“视线盲区”,救生员的凳子应该调高些还是矮些 (结果保留3位有效数字)
6.如图甲所示,自行车尾灯在夜晚被灯光照射时特别明亮。尾灯结构可简化成截面为等腰直角三角形的三棱镜,如图乙所示,AB边长为2L,A、D距离为L,一束单色光从D点垂直于AM面入射,恰好在AB面上发生全反射,已知光速为c。求:
(1)三棱镜的折射率;
(2)光在三棱镜中的传播时间。
7.发光二极管(LED)可高效地将电能转化为光能,在照明、平板显示、医疗器件等领域具有广泛的用途。有一种发光二极管,它由透明柱体和发光管芯组成。如图所示为一透明柱体的纵截面,柱体上半部分是球心为O、半径为R的半球体,M是球体的顶点,柱体下半部分是高度为R的圆柱体,其下表面的圆心为D、半径为R,管芯发光区域是半径为r且紧贴柱体下表面的圆面(PQ是直径,圆心也在D点)。
(1)若透明柱体的折射率n0=,真空中光速为c,求光从P点沿直线传播到M点的时间t;
(2)为使管芯发出的光到达球面时都不发生全反射,透明柱体的折射率n应满足什么条件
答案与分层梯度式解析
专题强化练6 折射和全反射在科技、生产、生活中的应用
1.A 设CD面上的入射角为θ,因为在CD和EA上发生全反射,且两次反射的入射角相等,作光路图如图所示。
根据几何关系有4θ=90°。解得θ=22.5°。当光刚好在CD和AE面上发生全反射时,折射率最小,有sin θ=,解得五棱镜的最小折射率为n=,故A正确。
2.C 复色光射入冰晶时,a光的折射角大于b光的折射角,由折射定律可知冰晶对a光的折射率小于对b光的折射率,故a光的频率比b光的频率小;根据v=,可知b光在冰晶中的传播速度较小,故A、B错误;由临界角公式sin C=可知,冰晶对b光的折射率大,故b光从冰晶射向空气时发生全反射的临界角小,C正确;由于v=λf,光在冰晶中的波长λ===λ0,由于a光在真空中的波长大于b光的波长,而冰晶对a光的折射率又小于对b光的,故a光在冰晶中的波长大于b光在冰晶中的波长,故D错误。
3.B 为使从立方体外面各个方向都看不到小气泡,纸片最小时,来自气泡的光恰好在纸片边缘发生全反射,由sin C==,得tan C=。由几何关系可知tan C=,S=πr2,得S=,故B正确。
关键点拨 画出恰好发生全反射时的临界光线,此情景对应的面积为纸片的最小面积。运用折射定律和几何知识求出该半径,从而求出面积即可。
4.D 两束光发生全反射的临界角C满足sin C===,而a、b两束光线第一次到达外侧圆弧的入射角分别满足sin αb==,sin αa==,可知αb>C,αa
5.答案 (1) (2)1.62 m 增大 调高些
解析 (1)来自P点的光线在水面发生折射后进入人眼,设入射角为r,折射角为i。由几何关系可知sin i=,sin r=,则水的折射率n=,联立各式代入数据解得n=。
(2)水深仅为H2=1.8 m时,设刚好能看到的最近点为P',来自P'点的光线在水面发生折射进入人眼时入射角和折射角均不变,光路图如图所示。
由几何关系得x2=H2 tan r+(H1-H2)tan i,代入数据解得x2≈1.62 m。
若水位降低时,该距离增大。
要减小“视线盲区”,则救生员的凳子应该调高些。
6.答案 (1) (2)L
解析 (1)光路如图所示。
光线恰好在AB面上发生全反射,则全反射临界角C=∠A=45°,
根据sin C=,解得n=。
(2)根据几何知识得AD=DE=FG=L,
AE==L,BF=BE=AB-AE=L,
则EF===2L,
则光在三棱镜中传播的路程为s=DE+EF+FG=4L,
光在三棱镜中的传播速度v=,
光在三棱镜中的传播时间t=,
解得t=L。
7.答案 (1) (2)n<
解析 (1)光在透明柱体中的传播速度为v=,
P到M点的距离为s=,
解得从P点沿直线传播到M点的时间为t==。
(2)光路图如图所示。
从P点射到N或从Q点射到N'点的光在球面处的入射角最大,设为i,则
sin i=,
设光发生全反射的临界角为C,则
sin C=,
不发生全反射,应满足sin i
7
同课章节目录
