16.2 线段的垂直平分线(第1课时)教学设计(表格式)冀教版数学八年级上册
文档属性
| 名称 | 16.2 线段的垂直平分线(第1课时)教学设计(表格式)冀教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 133.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 19:41:16 | ||
图片预览


文档简介
16.2 线段的垂直平分线
第1课时 线段垂直平分线的性质定理
课题 第1课时 线段垂直平分线的性质定理 课型 新授课
教学内容 教材第112-114页的内容
教学目标 1.理解和掌握线段的垂直平分线的性质定理. 2.能灵活运用线段的垂直平分线的性质定理解题,能解决最短路径问题. 3.通过经历线段的垂直平分线的性质定理的证明过程,体验逻辑推理的数学方法.
教学重难点 教学重点:1.线段的垂直平分线的性质定理. 2.能灵活运用线段的垂直平分线的性质定理解题. 教学难点:灵活运用线段的垂直平分线的性质定理解题.
教 学 过 程 备 注
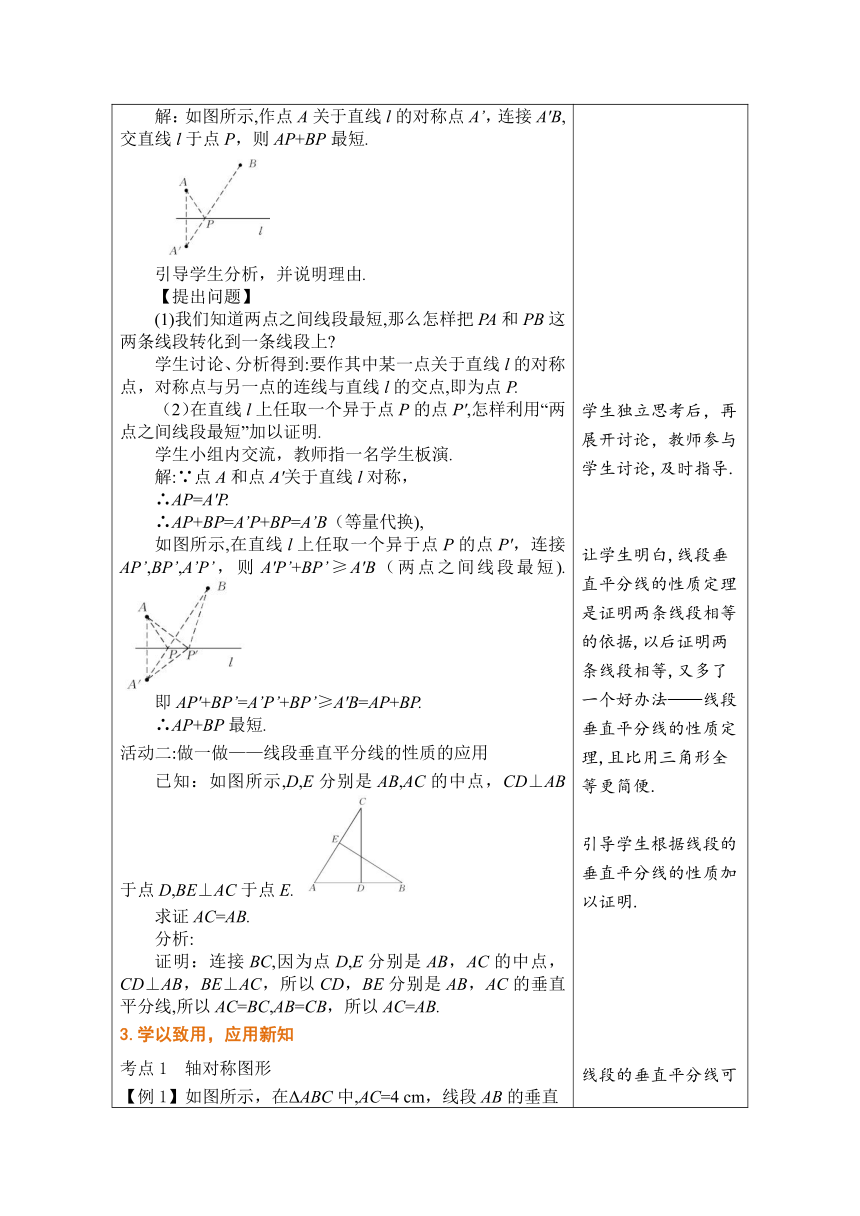
1.回顾旧知,引入课题 师:上节课我们共同探讨了轴对称图形,知道现实生活中由于有轴对称图形,而使世界更加美丽,那么大家想一想,线段是不是轴对称图形呢 它的对称轴是什么? 生:线段是轴对称图形,它的对称轴是线段的中垂线. 师:什么是线段的垂直平分线呢? 学生思考抢答. 师:很好,这节课我们来学习线段的垂直平分线的有关内容. 2.观察探究,学习新知 活动一:一起探究——线段垂直平分线的性质定理 如图所示,已知线段AB和它的中垂线l,O为垂足. 在直线上任取一点P,连接PA,PB,线段PA和线段PB有怎样的数量关系?提出你的猜想说明理由. 学生猜想得出:事实上,因为线段AB是轴对称图形,垂直平分线l是它的对称轴,所以线段AB沿对称轴l对折后,点A和点B重合,线段PA和线段PB重合,从而PA=PB. 我们来证明这个猜想的正确性. 请同学们先根据这个命题画出图形(如图所示),写出已知、求证. 已知:如图所示,线段AB和它的垂直平分线l,垂足为O,点P为直线l上任意一点,连接PA,PB. 求证PA=PB. 证明:在ΔPAO和ΔPBO中, ∵ ∴ΔPAO≌ΔPBO(SAS), ∴PA=PB(全等三角形的对应边相等). 教师说明:经过刚才的证明我们得到这个猜想是正确的. 由已经被证实的猜想,得到了线段垂直平分线的性质定理: 线段垂直平分线上的点到线段两端的距离相等. 师:分析定理的条件和结论. 点P在线段AB的垂直平分线上PA=PB. (条件) (结论) 【过渡语】了解了线段垂直平分线的性质定理,应用线段垂直平分线的性质定理可以解决一些问题. 【教材例题】 例1 已知:如图所示,点A,B是直线外的任意两点,在直线l上,试确定一点P,使AP+BP最短. 解:如图所示,作点A关于直线l的对称点A’,连接A'B,交直线l于点P,则AP+BP最短. 引导学生分析,并说明理由. 【提出问题】 (1)我们知道两点之间线段最短,那么怎样把PA和PB这两条线段转化到一条线段上 学生讨论、分析得到:要作其中某一点关于直线l的对称点,对称点与另一点的连线与直线l的交点,即为点P. (2)在直线l上任取一个异于点P的点P',怎样利用“两点之间线段最短”加以证明. 学生小组内交流,教师指一名学生板演. 解:∵点A和点A'关于直线l对称, ∴AP=A'P. ∴AP+BP=A’P+BP=A’B(等量代换), 如图所示,在直线l上任取一个异于点P的点P',连接AP’,BP’,A’P’,则A'P’+BP’≥A'B(两点之间线段最短). 即AP'+BP’=A’P’+BP’≥A'B=AP+BP. ∴AP+BP最短. 活动二:做一做——线段垂直平分线的性质的应用 已知:如图所示,D,E分别是AB,AC的中点,CD⊥AB于点D,BE⊥AC于点E. 求证AC=AB. 分析: 证明:连接BC,因为点D,E分别是AB,AC的中点,CD⊥AB,BE⊥AC,所以CD,BE分别是AB,AC的垂直平分线,所以AC=BC,AB=CB,所以AC=AB. 3.学以致用,应用新知 考点1 轴对称图形 【例1】如图所示,在ΔABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,ΔBCN的周长是7 cm,则BC的长为( ) A.1 cm B.2 cm C.3 cm D.4 cm 解析:∵MN是线段AB的垂直平分线,∴AN=BN, ∵ΔBCN的周长是7 cm,∴BN+NC+BC=7 cm, ∴AN+NC+BC=7 cm, ∵AN+NC=AC,∴AC+BC=7 cm, 又∵AC=4 cm,∴BC=7—4=3(cm).故选C. 答案:C 考点2 最短路径问题 【例2】如图,A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边的什么地方,可使所修的渠道最短? 作法:如图. (1)做点A关于a的对称点A'. (2)连接A'B,交a于点P. 点P即为抽水站的位置. 4.随堂训练,巩固新知 (1)如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( ) A.AB=AD B.CA平分∠BCD C.AB=BD D.△BEC≌△DEC 答案:C (2)如图,在△ ABC 中, BC 的垂直平分线交 BC 于点 D ,交 AB 于点 E ,连接 CE . 若 CE = CA ,∠ ACE =40°,则∠ B 的度数为 . (3)如图所示,已知DE是AC的垂直平分线,AB=10 cm,BC=11 cm,求ΔABD的周长. 解:∵DE垂直平分AC,∴AD=CD, ∴BD+AD=BD+CD=BC=11 cm, 又∵AB=10 cm, ∴ΔABD的周长为AB+BC=10+11=21(cm). 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)①线段垂直平分线的性质是线段垂直平分线上所有点都具有的特征,即线段垂直平分线上的每一个点到线段两端的距离都相等. ②这个定理向我们提供了一个证明两条线段相等的方法. (3)由性质定理的证明可知,要证明一个图形上每一个点都具有某种性质,只需要在图形上任取一点作代表即可,应注意理解和掌握这种由特殊到一般的思想方法. 6.布置作业 课本P113练习1-2题,P114习题A,B组. 用问题链的形式通过简单的复习导出本节课的教学内容,抢答有利于提高学生的学习积极性. 根据图形及既有经验,猜想关于线段垂直平分线的性质,并对猜想加以证明. 通过观察、猜想、证明让学生感受知识的形成过程,培养学生严谨的科学态度,进一步体会线段垂直平分线的性质定理. 引导学生利用SAS证明ΔPAO≌ΔPBO,从而得到PA=PB. 学生独立思考后,再展开讨论,教师参与学生讨论,及时指导. 让学生明白,线段垂直平分线的性质定理是证明两条线段相等的依据,以后证明两条线段相等,又多了一个好办法——线段垂直平分线的性质定理,且比用三角形全等更简便. 引导学生根据线段的垂直平分线的性质加以证明. 线段的垂直平分线可以实现线段的等量变换. 通过例题讲解,加深学生对线段垂直平分线性质的理解. 通过练习,巩固对线段垂直平分线的掌握程度. 先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可求出ΔABD的周长. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
板书设计 16.2 线段的垂直平分线 第1课时 线段垂直平分线的性质定理 提纲掣领,重点突出.
教后反思 1.线段垂直平分线在几何作图、证明、计算中有着十分重要的作用.线段的垂直平分线的性质定理是证明线段相等的重要途径.使学生通过观察、猜想得出结论.从而把知识的形成过程转化为学生亲自参与、发现、探索的过程. 2.引导学生分析性质定理的题设与结论,画图写出已知、求证,通过分析由学生得出证明性质定理的方法,这个过程既是探索过程,也是调动学生动脑思考的过程. 反思,更进一步提升.
第1课时 线段垂直平分线的性质定理
课题 第1课时 线段垂直平分线的性质定理 课型 新授课
教学内容 教材第112-114页的内容
教学目标 1.理解和掌握线段的垂直平分线的性质定理. 2.能灵活运用线段的垂直平分线的性质定理解题,能解决最短路径问题. 3.通过经历线段的垂直平分线的性质定理的证明过程,体验逻辑推理的数学方法.
教学重难点 教学重点:1.线段的垂直平分线的性质定理. 2.能灵活运用线段的垂直平分线的性质定理解题. 教学难点:灵活运用线段的垂直平分线的性质定理解题.
教 学 过 程 备 注
1.回顾旧知,引入课题 师:上节课我们共同探讨了轴对称图形,知道现实生活中由于有轴对称图形,而使世界更加美丽,那么大家想一想,线段是不是轴对称图形呢 它的对称轴是什么? 生:线段是轴对称图形,它的对称轴是线段的中垂线. 师:什么是线段的垂直平分线呢? 学生思考抢答. 师:很好,这节课我们来学习线段的垂直平分线的有关内容. 2.观察探究,学习新知 活动一:一起探究——线段垂直平分线的性质定理 如图所示,已知线段AB和它的中垂线l,O为垂足. 在直线上任取一点P,连接PA,PB,线段PA和线段PB有怎样的数量关系?提出你的猜想说明理由. 学生猜想得出:事实上,因为线段AB是轴对称图形,垂直平分线l是它的对称轴,所以线段AB沿对称轴l对折后,点A和点B重合,线段PA和线段PB重合,从而PA=PB. 我们来证明这个猜想的正确性. 请同学们先根据这个命题画出图形(如图所示),写出已知、求证. 已知:如图所示,线段AB和它的垂直平分线l,垂足为O,点P为直线l上任意一点,连接PA,PB. 求证PA=PB. 证明:在ΔPAO和ΔPBO中, ∵ ∴ΔPAO≌ΔPBO(SAS), ∴PA=PB(全等三角形的对应边相等). 教师说明:经过刚才的证明我们得到这个猜想是正确的. 由已经被证实的猜想,得到了线段垂直平分线的性质定理: 线段垂直平分线上的点到线段两端的距离相等. 师:分析定理的条件和结论. 点P在线段AB的垂直平分线上PA=PB. (条件) (结论) 【过渡语】了解了线段垂直平分线的性质定理,应用线段垂直平分线的性质定理可以解决一些问题. 【教材例题】 例1 已知:如图所示,点A,B是直线外的任意两点,在直线l上,试确定一点P,使AP+BP最短. 解:如图所示,作点A关于直线l的对称点A’,连接A'B,交直线l于点P,则AP+BP最短. 引导学生分析,并说明理由. 【提出问题】 (1)我们知道两点之间线段最短,那么怎样把PA和PB这两条线段转化到一条线段上 学生讨论、分析得到:要作其中某一点关于直线l的对称点,对称点与另一点的连线与直线l的交点,即为点P. (2)在直线l上任取一个异于点P的点P',怎样利用“两点之间线段最短”加以证明. 学生小组内交流,教师指一名学生板演. 解:∵点A和点A'关于直线l对称, ∴AP=A'P. ∴AP+BP=A’P+BP=A’B(等量代换), 如图所示,在直线l上任取一个异于点P的点P',连接AP’,BP’,A’P’,则A'P’+BP’≥A'B(两点之间线段最短). 即AP'+BP’=A’P’+BP’≥A'B=AP+BP. ∴AP+BP最短. 活动二:做一做——线段垂直平分线的性质的应用 已知:如图所示,D,E分别是AB,AC的中点,CD⊥AB于点D,BE⊥AC于点E. 求证AC=AB. 分析: 证明:连接BC,因为点D,E分别是AB,AC的中点,CD⊥AB,BE⊥AC,所以CD,BE分别是AB,AC的垂直平分线,所以AC=BC,AB=CB,所以AC=AB. 3.学以致用,应用新知 考点1 轴对称图形 【例1】如图所示,在ΔABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,ΔBCN的周长是7 cm,则BC的长为( ) A.1 cm B.2 cm C.3 cm D.4 cm 解析:∵MN是线段AB的垂直平分线,∴AN=BN, ∵ΔBCN的周长是7 cm,∴BN+NC+BC=7 cm, ∴AN+NC+BC=7 cm, ∵AN+NC=AC,∴AC+BC=7 cm, 又∵AC=4 cm,∴BC=7—4=3(cm).故选C. 答案:C 考点2 最短路径问题 【例2】如图,A,B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A,B两地,问该站建在河边的什么地方,可使所修的渠道最短? 作法:如图. (1)做点A关于a的对称点A'. (2)连接A'B,交a于点P. 点P即为抽水站的位置. 4.随堂训练,巩固新知 (1)如图,在四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( ) A.AB=AD B.CA平分∠BCD C.AB=BD D.△BEC≌△DEC 答案:C (2)如图,在△ ABC 中, BC 的垂直平分线交 BC 于点 D ,交 AB 于点 E ,连接 CE . 若 CE = CA ,∠ ACE =40°,则∠ B 的度数为 . (3)如图所示,已知DE是AC的垂直平分线,AB=10 cm,BC=11 cm,求ΔABD的周长. 解:∵DE垂直平分AC,∴AD=CD, ∴BD+AD=BD+CD=BC=11 cm, 又∵AB=10 cm, ∴ΔABD的周长为AB+BC=10+11=21(cm). 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)①线段垂直平分线的性质是线段垂直平分线上所有点都具有的特征,即线段垂直平分线上的每一个点到线段两端的距离都相等. ②这个定理向我们提供了一个证明两条线段相等的方法. (3)由性质定理的证明可知,要证明一个图形上每一个点都具有某种性质,只需要在图形上任取一点作代表即可,应注意理解和掌握这种由特殊到一般的思想方法. 6.布置作业 课本P113练习1-2题,P114习题A,B组. 用问题链的形式通过简单的复习导出本节课的教学内容,抢答有利于提高学生的学习积极性. 根据图形及既有经验,猜想关于线段垂直平分线的性质,并对猜想加以证明. 通过观察、猜想、证明让学生感受知识的形成过程,培养学生严谨的科学态度,进一步体会线段垂直平分线的性质定理. 引导学生利用SAS证明ΔPAO≌ΔPBO,从而得到PA=PB. 学生独立思考后,再展开讨论,教师参与学生讨论,及时指导. 让学生明白,线段垂直平分线的性质定理是证明两条线段相等的依据,以后证明两条线段相等,又多了一个好办法——线段垂直平分线的性质定理,且比用三角形全等更简便. 引导学生根据线段的垂直平分线的性质加以证明. 线段的垂直平分线可以实现线段的等量变换. 通过例题讲解,加深学生对线段垂直平分线性质的理解. 通过练习,巩固对线段垂直平分线的掌握程度. 先根据线段垂直平分线的性质得出AD=CD,故可得出BD+AD=BD+CD=BC,进而可求出ΔABD的周长. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
板书设计 16.2 线段的垂直平分线 第1课时 线段垂直平分线的性质定理 提纲掣领,重点突出.
教后反思 1.线段垂直平分线在几何作图、证明、计算中有着十分重要的作用.线段的垂直平分线的性质定理是证明线段相等的重要途径.使学生通过观察、猜想得出结论.从而把知识的形成过程转化为学生亲自参与、发现、探索的过程. 2.引导学生分析性质定理的题设与结论,画图写出已知、求证,通过分析由学生得出证明性质定理的方法,这个过程既是探索过程,也是调动学生动脑思考的过程. 反思,更进一步提升.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
