16.5 利用图形的平移、旋转和轴对称设计图案 教学设计(表格式)冀教版数学八年级上册
文档属性
| 名称 | 16.5 利用图形的平移、旋转和轴对称设计图案 教学设计(表格式)冀教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 351.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 19:47:07 | ||
图片预览


文档简介
16.5 利用图形的平移、旋转和轴对称设计图案
课题 16.4 利用图形的平移、旋转和轴对称设计图案 课型 新授课
教学内容 教材第128-130页的内容
教学目标 1.会运用平移、旋转、轴对称分析图案的形成过程,感受这些图案与变换的关系. 2.认识平移、旋转在现实生活中的应用. 3.能运用平移、旋转、轴对称进行简单的图案设计.
教学重难点 教学重点:1.中心对称的性质. 2.中心对称图形的有关概念. 教学难点:1.中心对称图形与轴对称图形的区别. 2.利用中心对称的性质和中心对称图形的有关概念解决问题.
教 学 过 程 备 注
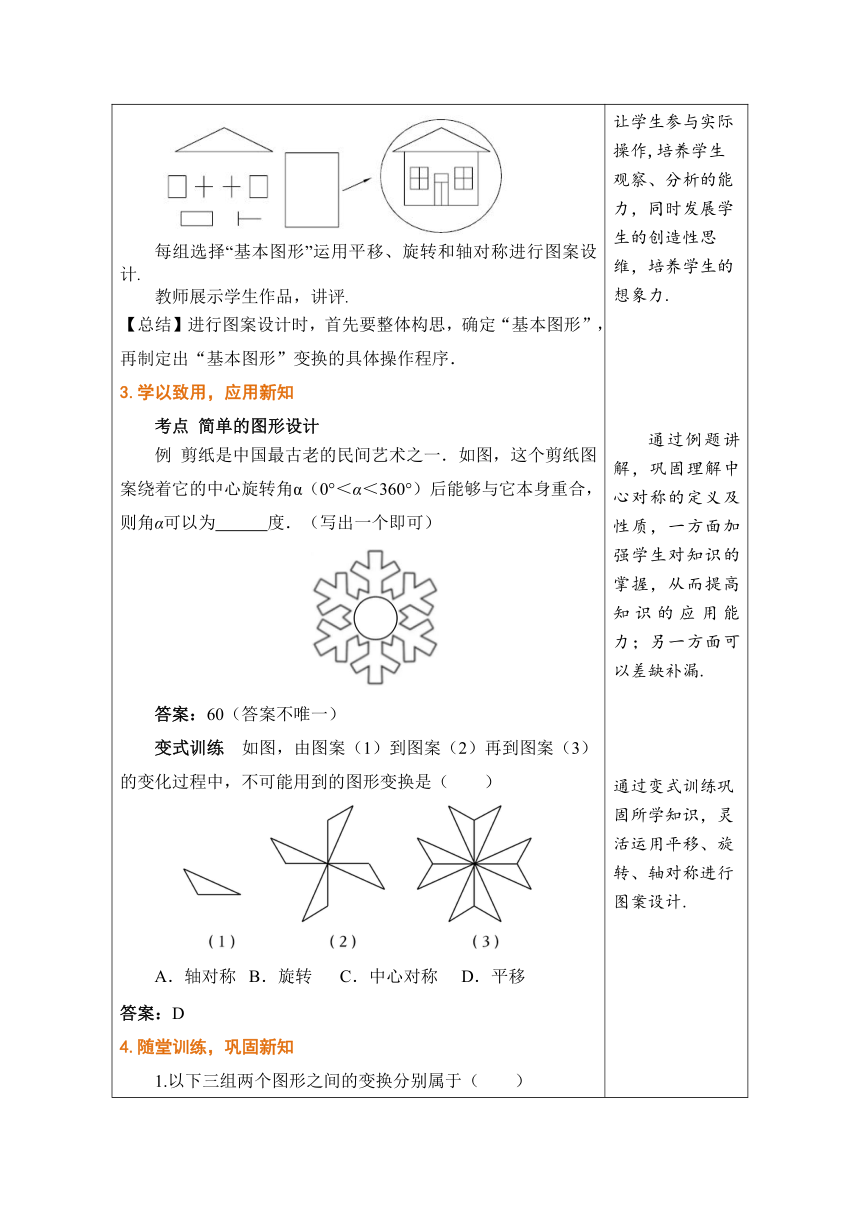
1.创设情境,导入课题 欣赏生活中的美丽图案:(多媒体展示,) 除这些图案外,还可以展示电风扇、螺旋桨等生活中的图片. 教师提问:请同学们欣赏这些图案,这些图案是怎样设计出来的?同学们想知道吗,那就让我们来探索吧! 2.观察探究,学习新知 活动一:试着做做——分析图案的形成 【试着做做】 (1)如图,请将这个图形沿箭头所示的方向和距离平移三次. (保留原图痕迹) (2)如图,将这个三角形绕两条虚线的交点,先旋转90 , 再将整个图形旋转180 ,画出旋转后的图形.(保留原图痕迹) 【观察与思考】 问题1: 观察两组图案,请你分别说说由图案(1)到图案(2)的变化过程. 问题2: 观察下图,请你说说由图案(1)到图案(2),再到图案(3)的变化过程. 经过观察,让学生发现: 问题1中的第1个图案可以看作是由基本图形一次轴对称得到;而第2个图案可以看作是由基本图形两次轴对称得到. 问题2可以看作是由基本图形(1)围绕旋转中心旋转120度,旋转两次得到(2),再把(2)旋转60度得到(3). 【总结】 (1)平面图案的形成方式:平移,旋转和轴对称. (2)图形的变换不改变图形的形状和大小,只改变图形的位置. 活动二:做一做——利用图形变换设计图案 如图所示,在同一平面内有一些几何图形,请利用图形的平移、旋转和轴对称,设计一个你想象中的“房屋示意图”. 每组选择“基本图形”运用平移、旋转和轴对称进行图案设计. 教师展示学生作品,讲评. 【总结】进行图案设计时,首先要整体构思,确定“基本图形”,再制定出“基本图形”变换的具体操作程序. 3.学以致用,应用新知 考点 简单的图形设计 例 剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角α(0°<α<360°)后能够与它本身重合,则角α可以为 度.(写出一个即可) 答案:60(答案不唯一) 变式训练 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( ) A.轴对称 B.旋转 C.中心对称 D.平移 答案:D 4.随堂训练,巩固新知 1.以下三组两个图形之间的变换分别属于( ) A.平移、旋转、旋转 B.平移、轴对称、轴对称 C.平移、轴对称、旋转 D.平移、旋转、轴对称 答案:D 2.第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角α(0°<α<360°)后能够与它本身重合,则角α可以为 度.(写出一个即可) 答案:60(答案不唯一) 3.下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形) (1)选取1个涂上阴影,使阴影部分组成一个轴对称图形,但不是中心对称图形; (2)选取1个涂上阴影,使阴影部分组成一个中心对称图形,但不是轴对称图形; (3)选取2个涂上阴影,使阴影部分组成一个轴对称图形. 解:(1)如图1所示. (2)如图2所示. (3)如图3所示. 4.某公司为了节约开支,购买了质量相同的两种颜色的残缺地砖,准备用来装修地面,现已加工成如图1所示的等腰直角三角形,王聪同学设计了如图2所示的四种图案. (1)你喜欢哪种图案?并简述该图案的形成过程. (2)请你利用所学过的知识再设计一幅与上述不同的图案. 解:(1)答案不唯一.我喜欢图案(3). 图案(3)的形成过程是:以两个不同颜色的三角形组成的正方形为“基本图形”,再将“基本图形”绕白色三角形的直角顶点顺时针(或逆时针)旋转90°,旋转3次得到. (2)如图所示: 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)“图案赏析”方法: 确定“基本图案”; 分析轴对称、平移、旋转等变换手法及组合的合理运用. (3)“图案设计”的整体构思: 突出主题:设计意图要求简捷、自然、别致,具有一定的意义; 构思图案:确定整幅图案的形状和“基本图案”; 形成图案:运用图形变换方式将“基本图案”演变成组合图案; 整理图案:对图案进行适当的修饰. 6.布置作业 课本P129练习1-2题,P130习题A,B组. 数学来源于实际生活,使学生感受到生活中处处有数学.创设问题情境,激发兴趣,调动学生的学习积极性,让学生充分感知轴对称、平移、旋转变换实际上就是所学过的全等变换,培养学生善于观察、善于总结、乐于探索研究的学习品质. 通过观察、辨析,分析一些复杂的图案可由一简单图形多次旋转或轴对称变化形成,让学生感受图案的形成过程和图案所展示的艺术美. 让学生在操作中明白,变换的方式可以是单一的一种,也可以多种变换综合而成. 让学生参与实际操作,培养学生观察、分析的能力,同时发展学生的创造性思维,培养学生的想象力. 通过例题讲解,巩固理解中心对称的定义及性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏. 通过变式训练巩固所学知识,灵活运用平移、旋转、轴对称进行图案设计. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
板书设计 16.4 中心对称图形 提纲掣领,重点突出.
教后反思 1.教师在教学过程中先让学生欣赏美丽的图案,体会平移、旋转和轴对称在图形中的应用.接着让学生动手操作,利用平移、旋转和轴对称设计出美丽的图案,然后让学生观察、讨论图案的形成过程,最后让学生综合应用轴对称、平移和旋转的方法,自己设计美丽的图案并进行交流和评比,让学生在体会成功的愉悦的同时感受数学美和数学方法的价值. 2.在课堂中应让学生欣赏、收集图案,在这个环节教师应多展示图片,课前让学生收集图片,引导学生发现美.从而让学生尝试设计图案,鼓励学生创造美,展示美,同时使学生体会到美丽的图案其实可以由一个简单的图形经过平移、旋转或轴对称得到,从而初步形成以简化繁的思想.这样可以愉悦学生心情,提高学生学习数学的兴趣. 反思,更进一步提升.
课题 16.4 利用图形的平移、旋转和轴对称设计图案 课型 新授课
教学内容 教材第128-130页的内容
教学目标 1.会运用平移、旋转、轴对称分析图案的形成过程,感受这些图案与变换的关系. 2.认识平移、旋转在现实生活中的应用. 3.能运用平移、旋转、轴对称进行简单的图案设计.
教学重难点 教学重点:1.中心对称的性质. 2.中心对称图形的有关概念. 教学难点:1.中心对称图形与轴对称图形的区别. 2.利用中心对称的性质和中心对称图形的有关概念解决问题.
教 学 过 程 备 注
1.创设情境,导入课题 欣赏生活中的美丽图案:(多媒体展示,) 除这些图案外,还可以展示电风扇、螺旋桨等生活中的图片. 教师提问:请同学们欣赏这些图案,这些图案是怎样设计出来的?同学们想知道吗,那就让我们来探索吧! 2.观察探究,学习新知 活动一:试着做做——分析图案的形成 【试着做做】 (1)如图,请将这个图形沿箭头所示的方向和距离平移三次. (保留原图痕迹) (2)如图,将这个三角形绕两条虚线的交点,先旋转90 , 再将整个图形旋转180 ,画出旋转后的图形.(保留原图痕迹) 【观察与思考】 问题1: 观察两组图案,请你分别说说由图案(1)到图案(2)的变化过程. 问题2: 观察下图,请你说说由图案(1)到图案(2),再到图案(3)的变化过程. 经过观察,让学生发现: 问题1中的第1个图案可以看作是由基本图形一次轴对称得到;而第2个图案可以看作是由基本图形两次轴对称得到. 问题2可以看作是由基本图形(1)围绕旋转中心旋转120度,旋转两次得到(2),再把(2)旋转60度得到(3). 【总结】 (1)平面图案的形成方式:平移,旋转和轴对称. (2)图形的变换不改变图形的形状和大小,只改变图形的位置. 活动二:做一做——利用图形变换设计图案 如图所示,在同一平面内有一些几何图形,请利用图形的平移、旋转和轴对称,设计一个你想象中的“房屋示意图”. 每组选择“基本图形”运用平移、旋转和轴对称进行图案设计. 教师展示学生作品,讲评. 【总结】进行图案设计时,首先要整体构思,确定“基本图形”,再制定出“基本图形”变换的具体操作程序. 3.学以致用,应用新知 考点 简单的图形设计 例 剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角α(0°<α<360°)后能够与它本身重合,则角α可以为 度.(写出一个即可) 答案:60(答案不唯一) 变式训练 如图,由图案(1)到图案(2)再到图案(3)的变化过程中,不可能用到的图形变换是( ) A.轴对称 B.旋转 C.中心对称 D.平移 答案:D 4.随堂训练,巩固新知 1.以下三组两个图形之间的变换分别属于( ) A.平移、旋转、旋转 B.平移、轴对称、轴对称 C.平移、轴对称、旋转 D.平移、旋转、轴对称 答案:D 2.第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角α(0°<α<360°)后能够与它本身重合,则角α可以为 度.(写出一个即可) 答案:60(答案不唯一) 3.下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形) (1)选取1个涂上阴影,使阴影部分组成一个轴对称图形,但不是中心对称图形; (2)选取1个涂上阴影,使阴影部分组成一个中心对称图形,但不是轴对称图形; (3)选取2个涂上阴影,使阴影部分组成一个轴对称图形. 解:(1)如图1所示. (2)如图2所示. (3)如图3所示. 4.某公司为了节约开支,购买了质量相同的两种颜色的残缺地砖,准备用来装修地面,现已加工成如图1所示的等腰直角三角形,王聪同学设计了如图2所示的四种图案. (1)你喜欢哪种图案?并简述该图案的形成过程. (2)请你利用所学过的知识再设计一幅与上述不同的图案. 解:(1)答案不唯一.我喜欢图案(3). 图案(3)的形成过程是:以两个不同颜色的三角形组成的正方形为“基本图形”,再将“基本图形”绕白色三角形的直角顶点顺时针(或逆时针)旋转90°,旋转3次得到. (2)如图所示: 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)“图案赏析”方法: 确定“基本图案”; 分析轴对称、平移、旋转等变换手法及组合的合理运用. (3)“图案设计”的整体构思: 突出主题:设计意图要求简捷、自然、别致,具有一定的意义; 构思图案:确定整幅图案的形状和“基本图案”; 形成图案:运用图形变换方式将“基本图案”演变成组合图案; 整理图案:对图案进行适当的修饰. 6.布置作业 课本P129练习1-2题,P130习题A,B组. 数学来源于实际生活,使学生感受到生活中处处有数学.创设问题情境,激发兴趣,调动学生的学习积极性,让学生充分感知轴对称、平移、旋转变换实际上就是所学过的全等变换,培养学生善于观察、善于总结、乐于探索研究的学习品质. 通过观察、辨析,分析一些复杂的图案可由一简单图形多次旋转或轴对称变化形成,让学生感受图案的形成过程和图案所展示的艺术美. 让学生在操作中明白,变换的方式可以是单一的一种,也可以多种变换综合而成. 让学生参与实际操作,培养学生观察、分析的能力,同时发展学生的创造性思维,培养学生的想象力. 通过例题讲解,巩固理解中心对称的定义及性质,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏. 通过变式训练巩固所学知识,灵活运用平移、旋转、轴对称进行图案设计. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
板书设计 16.4 中心对称图形 提纲掣领,重点突出.
教后反思 1.教师在教学过程中先让学生欣赏美丽的图案,体会平移、旋转和轴对称在图形中的应用.接着让学生动手操作,利用平移、旋转和轴对称设计出美丽的图案,然后让学生观察、讨论图案的形成过程,最后让学生综合应用轴对称、平移和旋转的方法,自己设计美丽的图案并进行交流和评比,让学生在体会成功的愉悦的同时感受数学美和数学方法的价值. 2.在课堂中应让学生欣赏、收集图案,在这个环节教师应多展示图片,课前让学生收集图片,引导学生发现美.从而让学生尝试设计图案,鼓励学生创造美,展示美,同时使学生体会到美丽的图案其实可以由一个简单的图形经过平移、旋转或轴对称得到,从而初步形成以简化繁的思想.这样可以愉悦学生心情,提高学生学习数学的兴趣. 反思,更进一步提升.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
