河北省邯郸市武安市贺进镇沙名中学、翟家庄中学2025年九年级下学期中考三模数学试卷(含详解)
文档属性
| 名称 | 河北省邯郸市武安市贺进镇沙名中学、翟家庄中学2025年九年级下学期中考三模数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 08:59:39 | ||
图片预览



文档简介
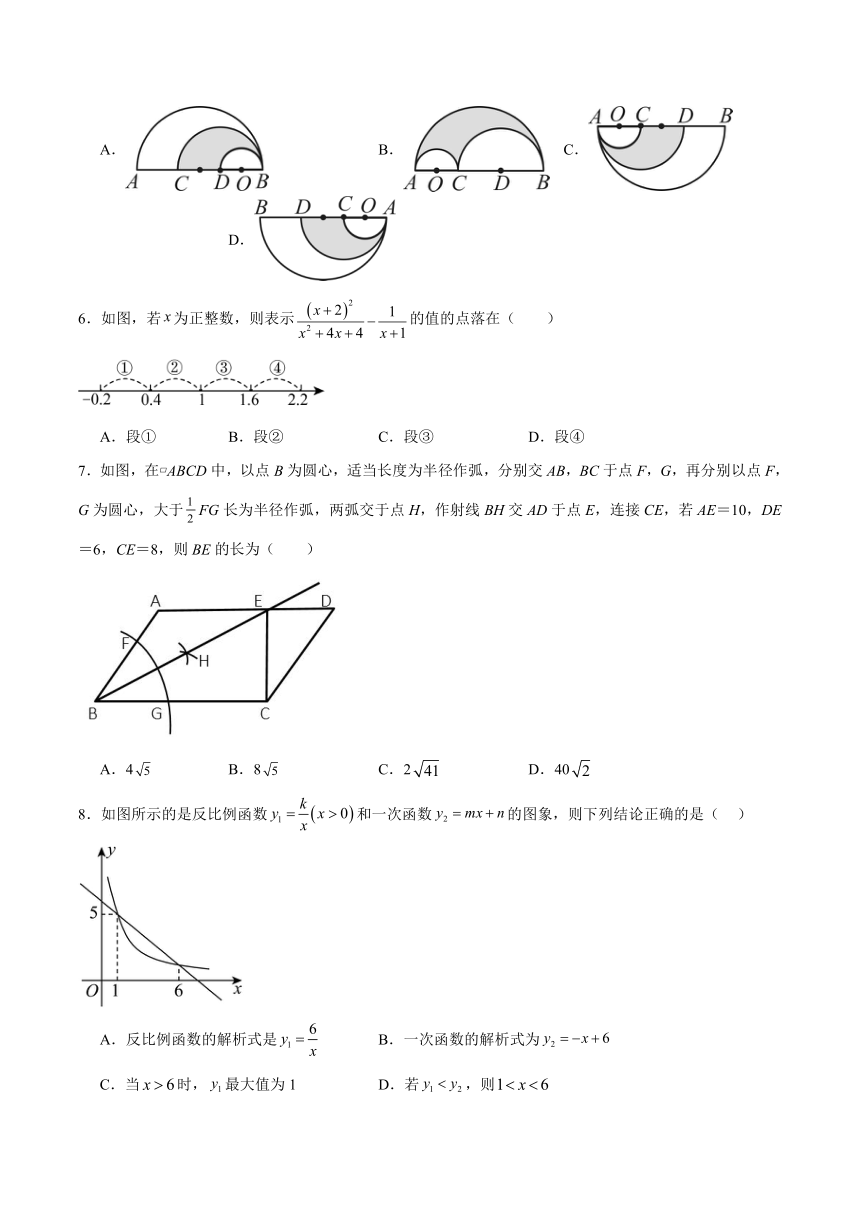
2025年河北省邯郸市武安市贺进镇沙名中学、翟家庄中学中考三模数学试题
一、单选题
1.墨迹覆盖了等式“”中的运算符号,则覆盖的是( )
A.+ B.- C.-或× D.+或÷
2.代数式可以表示成( )
A.3个相乘 B.个3相乘 C.3个相加 D.个3相加
3.下列运算正确的是( )
A. B.
C. D.
4.如图所示的正方体的表面展开图是( )
A. B.
C. D.
5.如图是由三个半圆组成的图形,点是最小半圆的圆心,且,此图形关于点成中心对称的图形是( )
A. B. C. D.
6.如图,若为正整数,则表示的值的点落在( )
A.段① B.段② C.段③ D.段④
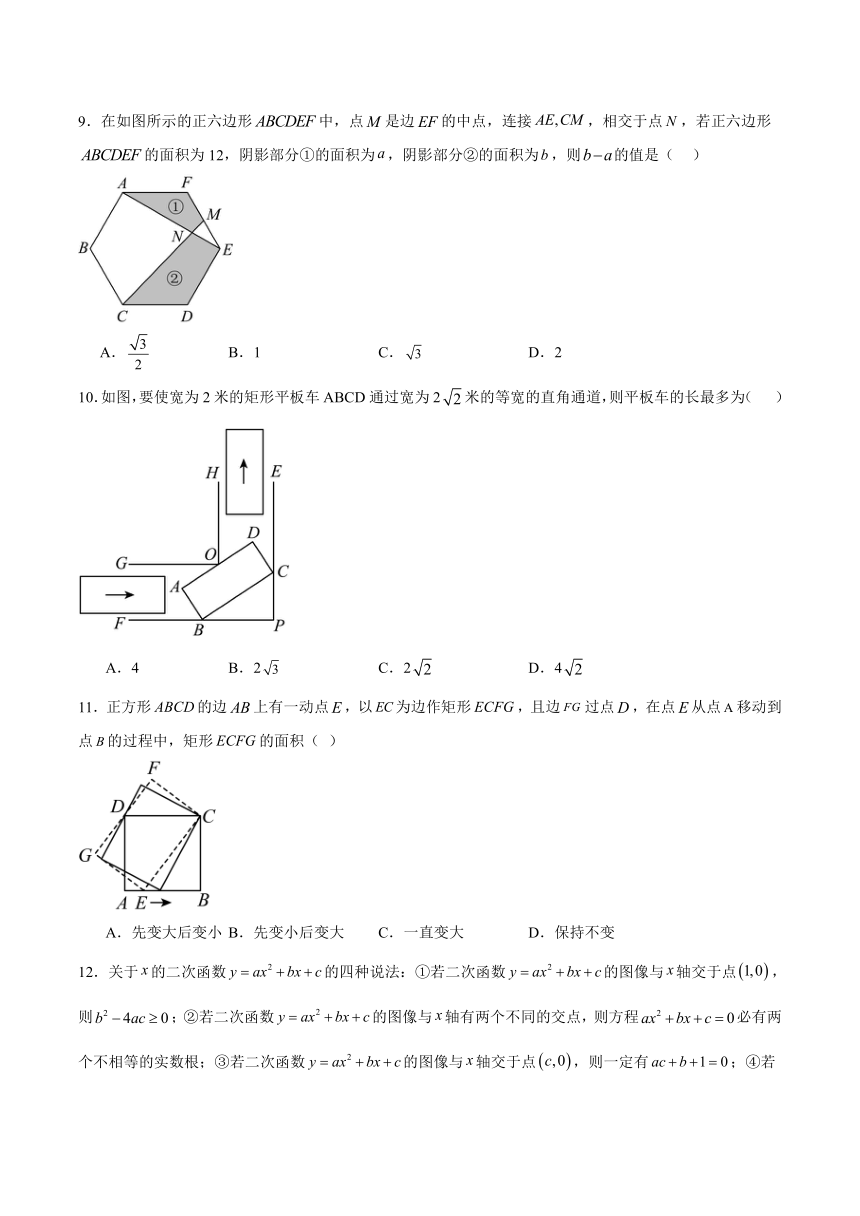
7.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以点F,G为圆心,大于FG长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE,若AE=10,DE=6,CE=8,则BE的长为( )
A.4 B.8 C.2 D.40
8.如图所示的是反比例函数和一次函数的图象,则下列结论正确的是( )
A.反比例函数的解析式是 B.一次函数的解析式为
C.当时,最大值为1 D.若,则
9.在如图所示的正六边形中,点是边的中点,连接,相交于点,若正六边形的面积为12,阴影部分①的面积为,阴影部分②的面积为,则的值是( )
A. B.1 C. D.2
10.如图,要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道,则平板车的长最多为( )
A.4 B.2 C.2 D.4
11.正方形的边上有一动点,以为边作矩形,且边过点,在点从点移动到点的过程中,矩形的面积( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
12.关于的二次函数的四种说法:①若二次函数的图像与轴交于点,则;②若二次函数的图像与轴有两个不同的交点,则方程必有两个不相等的实数根;③若二次函数的图像与轴交于点,则一定有;④若二次函数的图像与轴交于点,则,错误的是( )
A.① B.② C.③ D.④
二、填空题
13.若,则 .
14.如图,在多边形中,,,则 .
15.如图,在的正方形网格中,图中的点都在网格线的交点上.将点分别与点,连接,得到和,这四个三角形中与相似的是 .
16.两个反比例函数在第一象限内的图像如图所示,点在反比例函数的图像上,它们的横坐标分别是,纵坐标分别是1,3,5,……,共2025个连续奇数,过点分别作轴的平行线,与的图像的交点依次是,则的长为 .
三、解答题
17.嘉淇准备完成题目:计算:.发现有一个数“”印刷不清楚,
(1)他把“”猜成18,请你计算:;
(2)他妈说:“你猜错了,我看到该题标准答案的结果是.”通过计算说明原题中“”是几?
18.如图,数轴上,点,表示的数分别为,,点为负半轴上任意一点,它表示的数为.
计算的值;
在中,其中一个数是另两个数的平均数,求的值;
嘉琪认为:当时,,则以的长为边长不能构成三角形.若以的长为边长能构成三角形,请直接写出的取值范围.
19.探究:把四块如图1所示的小正方形按图2所示的方式拼成一个大正方形,空白部分是两个长为,宽为的互相垂直的矩形;
尝试:用不同的代数式表示图2中阴影部分的面积,可得到的等式为_____;
应用:如图3,已知是线段上一点,分别以为直角边向上和向下作等腰直角三角形,若,求阴影部分的面积;
拓展:已知,求的最小值.
20.为了提高同学们的文学鉴赏能力,某读书社全体成员在一段时间内开展阅读经典名著活动,活动结束后,把结果进行统计并制成如图1和图2所示的条形统计图和不完整的扇形统计图.
(1)该读书社一共有_____名成员,“2本”所在扇形的圆心角度数是_____;
(2)若阅读1本经典名著的成员中,有两名是女同学,一名是男同学,从中任意抽取两名同学,求恰好抽到的同学均为女同学的概率;
(3)若在同一时间段内,读书社之外某同学阅读经典名著本,把与读书社全体成员阅读经典名著本数的数据组成一组新的数据,发现平均数增大了,则的值至少为多少?
21.如图①,在矩形中,,点P、Q分别是、的中点,点E是折线段上一点.
(1)点C到直线距离的最大值是___________.
(2)如图②,以为直径,在的右侧作半圆O.
①当半圆O经过点D时,求半圆O被边所在直线截得的弧长;(注:, )
②当半圆O与边相切时,设切点为M,求的值;
(3)沿所在直线折叠矩形,已知点B的对应点为,若点恰好落在矩形的边上,直接写出的长.
22.如图,在平面直角坐标系中,点F的坐标为(0,10).点E的坐标为(20,0),直线l1经过点F和点E,直线l1与直线l2 、y=x相交于点P.
(1)求直线l1的表达式和点P的坐标;
(2)矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线l1或l2上,请直接写出此时t的值;
②若矩形ABCD在移动的过程中,直线CD交直线l1于点N,交直线l2于点M.当△PMN的面积等于18时,请直接写出此时t的值.
23.如图1和图2,在矩形中,,,点在边上,点,分别在,边上,且,点从点出发沿折线匀速运动,点在上随移动,且始终保持;点从点出发沿匀速运动,点,同时出发,点的速度是点的一半,点到达点停止,点随之停止.设点移动的路程为.
当点在上时,求点,的距离(用含的式子表示);
当时,求的值;
若,求的取值范围;
已知点从点到点再到点共用时秒,若,请直接写出点在线段上(包括端点)的总时长.
24.如图所示,抛物线与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接求面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与相似.若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.D
解:A选项中,,左右两边的值相等,A选项正确;
B选项中,,左右两边的值不相等,B选项错误;
C选项中,,,左右两边的值不相等,C选项错误;
D选项中,,,左右两边的值相等,D选项正确;
所以覆盖的是D选项,
故选:D.
2.A
解:∵,
∴可以表示成3个相乘,
故选:A.
3.A
解:A选项:,故A选项计算正确;
B选项:根据完全平方公式可得:,故B选项计算错误;
C选项:根据积的乘方可得:,故C选项计算错误;
D选项:根据平方差公式可得:,故D选项计算错误.
故选:A.
4.A
解:根据正方体的平面展开图的特征,B选项折叠后“菱形”和“圆”是相对面且在上面和下面;C选项折叠后“五角星”在正前面时,“圆”在下面,D选项折叠后,当“菱形”和“圆”在左侧和右侧且相对.在正面时,“正方形”在上面,“圆”在右侧面,故选项B、C、D均不合题意,
∴是该正方体的展开图的是A选项.
故选:A.
5.D
解:由中心对称图形的定义可知:此图形关于点成中心对称的图形是
.
故选:D.
6.B
解∵1.
又∵x为正整数,∴1,故表示的值的点落在②.
故选B.
7.B
解:由作法得BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD=AE+DE=10+6=16,AB=CD,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB,
∴AB=AE=10,
∴CD=10,
在△CDE中,∵DE=6,CE=8,CD=10,
∴DE2+CE2=CD2,
∴△CED为直角三角形,
∴∠CED=90°,
∵AD∥BC,
∴∠BCE=∠CED=90°,
在Rt△BCE中,BE=
故选:B.
8.D
解:A、由图象可知,两个函数图象相交于两个点,其中一个点坐标为,
把代入得,,
,选项错误,不符合题意;
B、当时,,
另一个交点坐标为:,
直线解析式为:,分别代入,,得:
,
解得,
,选项错误,不符合题意;
C、由图象可知,当时,随的增大而减小,当时,,选项错误,不符合题意;
D、由图象可知, ,直线在双曲线的下方,,选项正确,符合题意;
故选:D.
9.D
解:如图:连接,
由正六边形的对称性可知:,,
∴是全等的等边三角形
∴四边形是菱形
∴,
∵,
∴,
∵点是边的中点,
∴
∵
∴,
∴.
故选:D.
10.A
解:设平板手推车的长度为x米,当x为最大值,此时平板手推车所形成的△CBP为等腰直角三角形,连接PO与BC交于点N
∵直角通道的宽为2
∴PO=4m,
∴NP=PO-ON=4-2=2m
又∵△CBP为等腰直角三角形,
∴AD=BC=2CN=2NP=4m.
故答案为A.
11.D
连接DE,
∵S△CDE=S四边形CEGF,
S△CDE=S正方形ABCD,
∴矩形ECFG与正方形ABCD的面积相等.
故选D.
12.C
解:①图像过点,则代入得,此时二次方程至少有一个实根(),故判别式,原说法正确;
②图像与x轴有两个不同交点,说明方程有两个不等实根,故,原说法正确;
③图像过点,代入得,即,则或,原说法错误;
④若是方程的根,则,解得,代入,
则,原说法正确.
综上,错误的是③,
故选:C.
13.
解:
解得:.
故答案为:.
14./度
解:连接,如图:
,
∵五边形的内角和为:,,
∴,
∵,
∴,
∴,
∴,
故答案为:.
15.
解:的三边长分别为:,,;
的三边长分别为:,,,
∵,
∴与不相似;
的三边长分别为:,,;
∴,
∴;
的三边长分别为:,,,
∴,
∴与不相似;
的三边长分别为:,,,
∴,
∴与不相似;
故答案为:.
16.
解:第2025个奇数为,
的坐标为,
平行y轴,
的横坐标为,
的纵坐标为 ,
,
故答案为.
17.(1)-42;(2)-12
解:(1)
.
(2)设为,依题意得,.
解之得,.
18.(1)1;(2),;(3)
解:,
.
①当a为平均数时,得
解得;
②当x为平均数时,得
解得;
③当b为平均数时,得
,解得(不合题意,舍去).
.
由题意得,,
①当时
令,解得;
所以当时能构成三角形;
②当时能构成三角形.
综上.
19.尝试:,应用:12,扩展:2
解:尝试:,
故答案为:;
应用:设,
由题意,得.
又,
,
.
阴影部分的面积为.
拓展:,
的最小值为2.
20.(1),
(2)
(3)4
(1)解:根据题意得:成员总数为:,
,
故答案为:,;
(2)将两名女同学分别记为女1、女2,列表如下:
男 女1 女2
男 (男,女1) (男,女2)
女1 (女1,男) (女1,女2)
女2 (女2,男) (女2,女1)
一共有6种等可能的结果,其中均为女同学的结果有2种,
.
(3)读书社全体成员阅读经典名著本数的平均数为
添加一个后,平均数增大了,
.
又是正整数,
的值至少为4.
21.(1)5
(2)①,②
(3)或3
(1)解:当时,点C到直线的距离最大,
∵点P、Q分别是、的中点,
∴此时点C到直线距离为.
故答案为:5.
(2)(2)①如图,当半圆O经过点D时,点E恰好在点D处,
∵,
∴点C在半圆O上,连接,
在中,,
∴,
∴,
∴,
∴CQ弧长.
②或,
情况一:如图,当点E在线段上时,连接,延长交于点N,
∵与半圆相切于点,
∴,
∵四边形是矩形,
∴,
∴四边形是矩形,
∴,
∵,
∴,
在中,设,
∵,
∴,
解得,
∴,
∵,
∴,
情况二:如图,当点E在边上时,点M与点E重合,
∴,
∴四边形是矩形,
∴,,
∴.
综上所述,的值为或.
(3)(3)或3,
情况一:如图当点E在上时,,
在中,,
解得:.
情况二:如图,当点E在边上时,连接、,
则,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
综上所述,或3.
22.(1)直线l1的表达式为y=﹣x+10,点P坐标为(8,6);(2)①t值为或;②当t=时,△PMN的面积等于18.
(1)设直线l1的表达式为y=kx+b,
∵直线l1过点F(0,10),E(20,0),
∴,解得:,
直线l1的表达式为y=﹣x+10,
解方程组得,
∴点P坐标为(8,6);
(2)①如图,当点D在直线上l2时,
∵AD=9
∴点D与点A的横坐标之差为9,
∴将直线l1与直线l2 的解析式变形为x=20﹣2y,x=y,
∴y﹣(20﹣2y)=9,
解得:y=,
∴x=20﹣2y=,
则点A的坐标为:(,),
则AF=,
∵点A速度为每秒个单位,
∴t=;
如图,当点B在l2 直线上时,
∵AB=6,
∴点A的纵坐标比点B的纵坐标高6个单位,
∴直线l1的解析式减去直线l2 的解析式得,
﹣x+10﹣x=6,
解得x=,
y=﹣x+10=,
则点A坐标为(,)
则AF=,
∵点A速度为每秒个单位,
∴t=,
故t值为或;
②如图,
设直线AB交l2 于点H,
设点A横坐标为a,则点D横坐标为a+9,
由①中方法可知:MN=,
此时点P到MN距离为:a+9﹣8=a+1,
∵△PMN的面积等于18,
∴=18,
解得
a1=-1,a2=﹣-1(舍去),
∴AF=6﹣,
则此时t为,
当t=时,△PMN的面积等于18.
23.(1)(2)tan;(3)的取值范围是或;(4)秒
解:当点在上时,
∵,四边形ABCD是矩形,
∴,
设,则,
∴,,
∴.
当时,点在上时
∴,.
∴.
∵,,
.
①当点在上时,四边形是矩形
.
此时.
②当点在上时
,
而,
又
若,则.
,即.
.
.
综上的取值范围是:或.
解:点的运动速度单位长度/秒.
①若点在上,点与点重合时
.
即.
点到达点时
,.
当时点在线段上.
②若点在上(不含点),则.
则,即.
.
当时,.
解得:,.
当点与点重合时,
即,解得:.
当或时点在线段上.
综上点在线段上的总时长为秒.
24.(1) (0,-3),(1,-4);(2) ,();(3) G点坐标存在,为(2,-3)或(4,5)或(-2,5);(4) P点坐标存在,为或.
解:(1)令中x=0,此时y=-3,故C点坐标为(0,-3),
又二次函数的顶点坐标为,代入数据解得M点坐标为,
故答案为:C点坐标为(0,-3), M点坐标为(1,-4);
(2) 过N点作x轴的垂线交直线BC于Q点,连接BN,CN,如下图所示:
令中y=0,解得B(3,0),A(-1,0),
设直线BC的解析式为:,代入C(0,-3),B(3,0),
∴,解得,即直线BC的解析式为:,
设N点坐标为(),故Q点坐标为,其中,
则
,其中分别表示Q,C,B三点的横坐标,
且,,
故,其中,
当时,有最大值为,
此时N的坐标为(),
故答案为:有最大值为,N的坐标为();
(3) 设D点坐标为(1,t),G点坐标为(),且B(3,0),C(0,-3)
分类讨论:
情况①:当DG为对角线时,则另一对角线是BC,由中点坐标公式可知:
线段DG的中点坐标为,即,
线段BC的中点坐标为,即,
此时DG的中点与BC的中点为同一个点,
故,解得,
检验此时四边形DCGB为平行四边形,此时G坐标为(2,-3);
情况②:当DB为对角线时,则另一对角线是GC,由中点坐标公式可知:
线段DB的中点坐标为,即,
线段GC的中点坐标为,即,
此时DB的中点与GC的中点为同一个点,
故,解得,
检验此时四边形DCBG为平行四边形,此时G坐标为(4,5);
情况③:当DC为对角线时,则另一对角线是GB,由中点坐标公式可知:
线段DC的中点坐标为,即,
线段GB的中点坐标为,即,
此时DB的中点与GC的中点为同一个点,
故,解得,
检验此时四边形DGCB为平行四边形,此时G坐标为(-2,5);
综上所述,G点坐标存在,为(2,-3)或(4,5)或(-2,5);
(4) 连接AC,OP,如下图所示,
设MC的解析式为:y=kx+m,代入C(0,-3),M(1,-4)
即,解得
∴MC的解析式为:,令,求得E点坐标为(-3,0),
∴OE=OB=3,且OC=OC,
∴CE=CB,即∠B=∠E,
设P(x,-x-3),又∵P点在线段EC上,∴-3则,,
由题意知:△PEO相似△ABC,
分类讨论:
情况①:
∴,解得,满足-3情况②:
∴,解得,满足-3综上所述,P点的坐标为或.
一、单选题
1.墨迹覆盖了等式“”中的运算符号,则覆盖的是( )
A.+ B.- C.-或× D.+或÷
2.代数式可以表示成( )
A.3个相乘 B.个3相乘 C.3个相加 D.个3相加
3.下列运算正确的是( )
A. B.
C. D.
4.如图所示的正方体的表面展开图是( )
A. B.
C. D.
5.如图是由三个半圆组成的图形,点是最小半圆的圆心,且,此图形关于点成中心对称的图形是( )
A. B. C. D.
6.如图,若为正整数,则表示的值的点落在( )
A.段① B.段② C.段③ D.段④
7.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以点F,G为圆心,大于FG长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE,若AE=10,DE=6,CE=8,则BE的长为( )
A.4 B.8 C.2 D.40
8.如图所示的是反比例函数和一次函数的图象,则下列结论正确的是( )
A.反比例函数的解析式是 B.一次函数的解析式为
C.当时,最大值为1 D.若,则
9.在如图所示的正六边形中,点是边的中点,连接,相交于点,若正六边形的面积为12,阴影部分①的面积为,阴影部分②的面积为,则的值是( )
A. B.1 C. D.2
10.如图,要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道,则平板车的长最多为( )
A.4 B.2 C.2 D.4
11.正方形的边上有一动点,以为边作矩形,且边过点,在点从点移动到点的过程中,矩形的面积( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
12.关于的二次函数的四种说法:①若二次函数的图像与轴交于点,则;②若二次函数的图像与轴有两个不同的交点,则方程必有两个不相等的实数根;③若二次函数的图像与轴交于点,则一定有;④若二次函数的图像与轴交于点,则,错误的是( )
A.① B.② C.③ D.④
二、填空题
13.若,则 .
14.如图,在多边形中,,,则 .
15.如图,在的正方形网格中,图中的点都在网格线的交点上.将点分别与点,连接,得到和,这四个三角形中与相似的是 .
16.两个反比例函数在第一象限内的图像如图所示,点在反比例函数的图像上,它们的横坐标分别是,纵坐标分别是1,3,5,……,共2025个连续奇数,过点分别作轴的平行线,与的图像的交点依次是,则的长为 .
三、解答题
17.嘉淇准备完成题目:计算:.发现有一个数“”印刷不清楚,
(1)他把“”猜成18,请你计算:;
(2)他妈说:“你猜错了,我看到该题标准答案的结果是.”通过计算说明原题中“”是几?
18.如图,数轴上,点,表示的数分别为,,点为负半轴上任意一点,它表示的数为.
计算的值;
在中,其中一个数是另两个数的平均数,求的值;
嘉琪认为:当时,,则以的长为边长不能构成三角形.若以的长为边长能构成三角形,请直接写出的取值范围.
19.探究:把四块如图1所示的小正方形按图2所示的方式拼成一个大正方形,空白部分是两个长为,宽为的互相垂直的矩形;
尝试:用不同的代数式表示图2中阴影部分的面积,可得到的等式为_____;
应用:如图3,已知是线段上一点,分别以为直角边向上和向下作等腰直角三角形,若,求阴影部分的面积;
拓展:已知,求的最小值.
20.为了提高同学们的文学鉴赏能力,某读书社全体成员在一段时间内开展阅读经典名著活动,活动结束后,把结果进行统计并制成如图1和图2所示的条形统计图和不完整的扇形统计图.
(1)该读书社一共有_____名成员,“2本”所在扇形的圆心角度数是_____;
(2)若阅读1本经典名著的成员中,有两名是女同学,一名是男同学,从中任意抽取两名同学,求恰好抽到的同学均为女同学的概率;
(3)若在同一时间段内,读书社之外某同学阅读经典名著本,把与读书社全体成员阅读经典名著本数的数据组成一组新的数据,发现平均数增大了,则的值至少为多少?
21.如图①,在矩形中,,点P、Q分别是、的中点,点E是折线段上一点.
(1)点C到直线距离的最大值是___________.
(2)如图②,以为直径,在的右侧作半圆O.
①当半圆O经过点D时,求半圆O被边所在直线截得的弧长;(注:, )
②当半圆O与边相切时,设切点为M,求的值;
(3)沿所在直线折叠矩形,已知点B的对应点为,若点恰好落在矩形的边上,直接写出的长.
22.如图,在平面直角坐标系中,点F的坐标为(0,10).点E的坐标为(20,0),直线l1经过点F和点E,直线l1与直线l2 、y=x相交于点P.
(1)求直线l1的表达式和点P的坐标;
(2)矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线l1或l2上,请直接写出此时t的值;
②若矩形ABCD在移动的过程中,直线CD交直线l1于点N,交直线l2于点M.当△PMN的面积等于18时,请直接写出此时t的值.
23.如图1和图2,在矩形中,,,点在边上,点,分别在,边上,且,点从点出发沿折线匀速运动,点在上随移动,且始终保持;点从点出发沿匀速运动,点,同时出发,点的速度是点的一半,点到达点停止,点随之停止.设点移动的路程为.
当点在上时,求点,的距离(用含的式子表示);
当时,求的值;
若,求的取值范围;
已知点从点到点再到点共用时秒,若,请直接写出点在线段上(包括端点)的总时长.
24.如图所示,抛物线与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接求面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与相似.若存在,求出点P的坐标;若不存在,请说明理由.
参考答案
1.D
解:A选项中,,左右两边的值相等,A选项正确;
B选项中,,左右两边的值不相等,B选项错误;
C选项中,,,左右两边的值不相等,C选项错误;
D选项中,,,左右两边的值相等,D选项正确;
所以覆盖的是D选项,
故选:D.
2.A
解:∵,
∴可以表示成3个相乘,
故选:A.
3.A
解:A选项:,故A选项计算正确;
B选项:根据完全平方公式可得:,故B选项计算错误;
C选项:根据积的乘方可得:,故C选项计算错误;
D选项:根据平方差公式可得:,故D选项计算错误.
故选:A.
4.A
解:根据正方体的平面展开图的特征,B选项折叠后“菱形”和“圆”是相对面且在上面和下面;C选项折叠后“五角星”在正前面时,“圆”在下面,D选项折叠后,当“菱形”和“圆”在左侧和右侧且相对.在正面时,“正方形”在上面,“圆”在右侧面,故选项B、C、D均不合题意,
∴是该正方体的展开图的是A选项.
故选:A.
5.D
解:由中心对称图形的定义可知:此图形关于点成中心对称的图形是
.
故选:D.
6.B
解∵1.
又∵x为正整数,∴1,故表示的值的点落在②.
故选B.
7.B
解:由作法得BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD=AE+DE=10+6=16,AB=CD,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB,
∴AB=AE=10,
∴CD=10,
在△CDE中,∵DE=6,CE=8,CD=10,
∴DE2+CE2=CD2,
∴△CED为直角三角形,
∴∠CED=90°,
∵AD∥BC,
∴∠BCE=∠CED=90°,
在Rt△BCE中,BE=
故选:B.
8.D
解:A、由图象可知,两个函数图象相交于两个点,其中一个点坐标为,
把代入得,,
,选项错误,不符合题意;
B、当时,,
另一个交点坐标为:,
直线解析式为:,分别代入,,得:
,
解得,
,选项错误,不符合题意;
C、由图象可知,当时,随的增大而减小,当时,,选项错误,不符合题意;
D、由图象可知, ,直线在双曲线的下方,,选项正确,符合题意;
故选:D.
9.D
解:如图:连接,
由正六边形的对称性可知:,,
∴是全等的等边三角形
∴四边形是菱形
∴,
∵,
∴,
∵点是边的中点,
∴
∵
∴,
∴.
故选:D.
10.A
解:设平板手推车的长度为x米,当x为最大值,此时平板手推车所形成的△CBP为等腰直角三角形,连接PO与BC交于点N
∵直角通道的宽为2
∴PO=4m,
∴NP=PO-ON=4-2=2m
又∵△CBP为等腰直角三角形,
∴AD=BC=2CN=2NP=4m.
故答案为A.
11.D
连接DE,
∵S△CDE=S四边形CEGF,
S△CDE=S正方形ABCD,
∴矩形ECFG与正方形ABCD的面积相等.
故选D.
12.C
解:①图像过点,则代入得,此时二次方程至少有一个实根(),故判别式,原说法正确;
②图像与x轴有两个不同交点,说明方程有两个不等实根,故,原说法正确;
③图像过点,代入得,即,则或,原说法错误;
④若是方程的根,则,解得,代入,
则,原说法正确.
综上,错误的是③,
故选:C.
13.
解:
解得:.
故答案为:.
14./度
解:连接,如图:
,
∵五边形的内角和为:,,
∴,
∵,
∴,
∴,
∴,
故答案为:.
15.
解:的三边长分别为:,,;
的三边长分别为:,,,
∵,
∴与不相似;
的三边长分别为:,,;
∴,
∴;
的三边长分别为:,,,
∴,
∴与不相似;
的三边长分别为:,,,
∴,
∴与不相似;
故答案为:.
16.
解:第2025个奇数为,
的坐标为,
平行y轴,
的横坐标为,
的纵坐标为 ,
,
故答案为.
17.(1)-42;(2)-12
解:(1)
.
(2)设为,依题意得,.
解之得,.
18.(1)1;(2),;(3)
解:,
.
①当a为平均数时,得
解得;
②当x为平均数时,得
解得;
③当b为平均数时,得
,解得(不合题意,舍去).
.
由题意得,,
①当时
令,解得;
所以当时能构成三角形;
②当时能构成三角形.
综上.
19.尝试:,应用:12,扩展:2
解:尝试:,
故答案为:;
应用:设,
由题意,得.
又,
,
.
阴影部分的面积为.
拓展:,
的最小值为2.
20.(1),
(2)
(3)4
(1)解:根据题意得:成员总数为:,
,
故答案为:,;
(2)将两名女同学分别记为女1、女2,列表如下:
男 女1 女2
男 (男,女1) (男,女2)
女1 (女1,男) (女1,女2)
女2 (女2,男) (女2,女1)
一共有6种等可能的结果,其中均为女同学的结果有2种,
.
(3)读书社全体成员阅读经典名著本数的平均数为
添加一个后,平均数增大了,
.
又是正整数,
的值至少为4.
21.(1)5
(2)①,②
(3)或3
(1)解:当时,点C到直线的距离最大,
∵点P、Q分别是、的中点,
∴此时点C到直线距离为.
故答案为:5.
(2)(2)①如图,当半圆O经过点D时,点E恰好在点D处,
∵,
∴点C在半圆O上,连接,
在中,,
∴,
∴,
∴,
∴CQ弧长.
②或,
情况一:如图,当点E在线段上时,连接,延长交于点N,
∵与半圆相切于点,
∴,
∵四边形是矩形,
∴,
∴四边形是矩形,
∴,
∵,
∴,
在中,设,
∵,
∴,
解得,
∴,
∵,
∴,
情况二:如图,当点E在边上时,点M与点E重合,
∴,
∴四边形是矩形,
∴,,
∴.
综上所述,的值为或.
(3)(3)或3,
情况一:如图当点E在上时,,
在中,,
解得:.
情况二:如图,当点E在边上时,连接、,
则,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
综上所述,或3.
22.(1)直线l1的表达式为y=﹣x+10,点P坐标为(8,6);(2)①t值为或;②当t=时,△PMN的面积等于18.
(1)设直线l1的表达式为y=kx+b,
∵直线l1过点F(0,10),E(20,0),
∴,解得:,
直线l1的表达式为y=﹣x+10,
解方程组得,
∴点P坐标为(8,6);
(2)①如图,当点D在直线上l2时,
∵AD=9
∴点D与点A的横坐标之差为9,
∴将直线l1与直线l2 的解析式变形为x=20﹣2y,x=y,
∴y﹣(20﹣2y)=9,
解得:y=,
∴x=20﹣2y=,
则点A的坐标为:(,),
则AF=,
∵点A速度为每秒个单位,
∴t=;
如图,当点B在l2 直线上时,
∵AB=6,
∴点A的纵坐标比点B的纵坐标高6个单位,
∴直线l1的解析式减去直线l2 的解析式得,
﹣x+10﹣x=6,
解得x=,
y=﹣x+10=,
则点A坐标为(,)
则AF=,
∵点A速度为每秒个单位,
∴t=,
故t值为或;
②如图,
设直线AB交l2 于点H,
设点A横坐标为a,则点D横坐标为a+9,
由①中方法可知:MN=,
此时点P到MN距离为:a+9﹣8=a+1,
∵△PMN的面积等于18,
∴=18,
解得
a1=-1,a2=﹣-1(舍去),
∴AF=6﹣,
则此时t为,
当t=时,△PMN的面积等于18.
23.(1)(2)tan;(3)的取值范围是或;(4)秒
解:当点在上时,
∵,四边形ABCD是矩形,
∴,
设,则,
∴,,
∴.
当时,点在上时
∴,.
∴.
∵,,
.
①当点在上时,四边形是矩形
.
此时.
②当点在上时
,
而,
又
若,则.
,即.
.
.
综上的取值范围是:或.
解:点的运动速度单位长度/秒.
①若点在上,点与点重合时
.
即.
点到达点时
,.
当时点在线段上.
②若点在上(不含点),则.
则,即.
.
当时,.
解得:,.
当点与点重合时,
即,解得:.
当或时点在线段上.
综上点在线段上的总时长为秒.
24.(1) (0,-3),(1,-4);(2) ,();(3) G点坐标存在,为(2,-3)或(4,5)或(-2,5);(4) P点坐标存在,为或.
解:(1)令中x=0,此时y=-3,故C点坐标为(0,-3),
又二次函数的顶点坐标为,代入数据解得M点坐标为,
故答案为:C点坐标为(0,-3), M点坐标为(1,-4);
(2) 过N点作x轴的垂线交直线BC于Q点,连接BN,CN,如下图所示:
令中y=0,解得B(3,0),A(-1,0),
设直线BC的解析式为:,代入C(0,-3),B(3,0),
∴,解得,即直线BC的解析式为:,
设N点坐标为(),故Q点坐标为,其中,
则
,其中分别表示Q,C,B三点的横坐标,
且,,
故,其中,
当时,有最大值为,
此时N的坐标为(),
故答案为:有最大值为,N的坐标为();
(3) 设D点坐标为(1,t),G点坐标为(),且B(3,0),C(0,-3)
分类讨论:
情况①:当DG为对角线时,则另一对角线是BC,由中点坐标公式可知:
线段DG的中点坐标为,即,
线段BC的中点坐标为,即,
此时DG的中点与BC的中点为同一个点,
故,解得,
检验此时四边形DCGB为平行四边形,此时G坐标为(2,-3);
情况②:当DB为对角线时,则另一对角线是GC,由中点坐标公式可知:
线段DB的中点坐标为,即,
线段GC的中点坐标为,即,
此时DB的中点与GC的中点为同一个点,
故,解得,
检验此时四边形DCBG为平行四边形,此时G坐标为(4,5);
情况③:当DC为对角线时,则另一对角线是GB,由中点坐标公式可知:
线段DC的中点坐标为,即,
线段GB的中点坐标为,即,
此时DB的中点与GC的中点为同一个点,
故,解得,
检验此时四边形DGCB为平行四边形,此时G坐标为(-2,5);
综上所述,G点坐标存在,为(2,-3)或(4,5)或(-2,5);
(4) 连接AC,OP,如下图所示,
设MC的解析式为:y=kx+m,代入C(0,-3),M(1,-4)
即,解得
∴MC的解析式为:,令,求得E点坐标为(-3,0),
∴OE=OB=3,且OC=OC,
∴CE=CB,即∠B=∠E,
设P(x,-x-3),又∵P点在线段EC上,∴-3
由题意知:△PEO相似△ABC,
分类讨论:
情况①:
∴,解得,满足-3
∴,解得,满足-3
同课章节目录
