17.3 勾股定理(第1课时)教学设计(表格式)冀教版数学八年级上册
文档属性
| 名称 | 17.3 勾股定理(第1课时)教学设计(表格式)冀教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 218.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 19:47:55 | ||
图片预览

文档简介
17.3 勾股定理
第1课时 勾股定理
课题 第1课时 勾股定理 课型 新授课
教学内容 教材第150-152页的内容
教学目标 1.经历探索勾股定理的过程,发展对图形性质或数量关系猜想的能力,体会拼图验证的合理性. 2.掌握勾股定理. 3.在探索的过程中,体会数形结合、由特殊到一般及化归等数学思想方法.
教学重难点 教学重点:勾股定理的探索过程. 教学难点:勾股定理的简单运用.
教 学 过 程 备 注
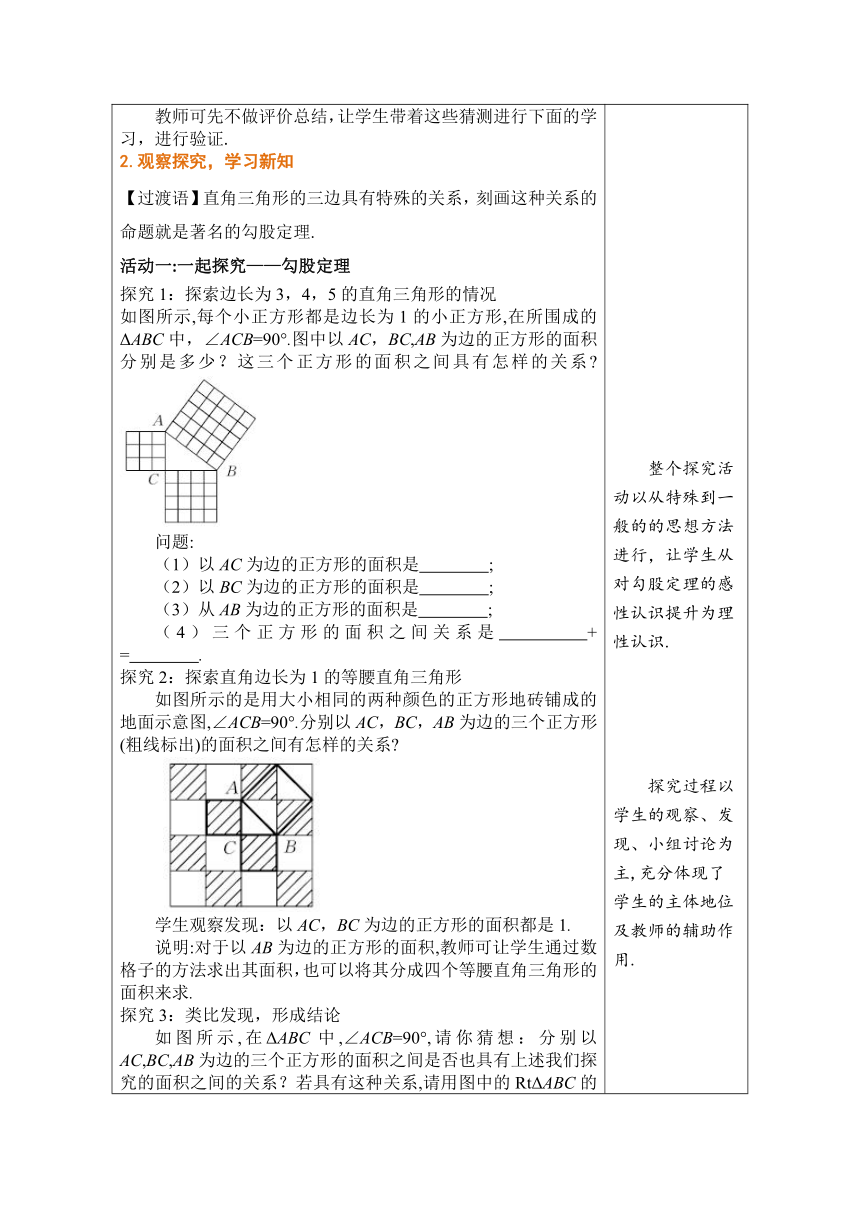
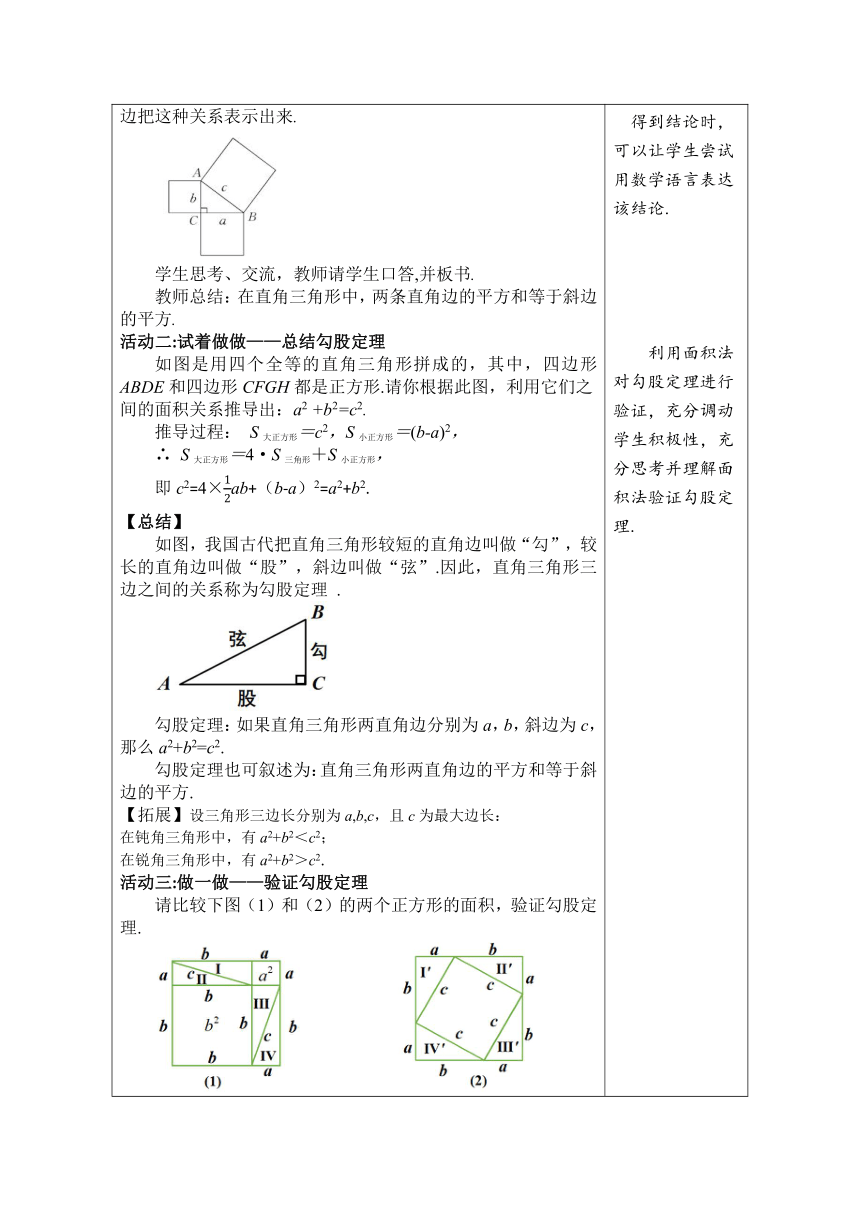
1.创设情境,引入课题 2002年第24届世界数学家大会在我国北京召开,图片显示的是本届世界数学家大会的会标: 问题1:观察会标,这个图案是由哪些基本图形组成? 学生:这个图形由四个全等的直角三角形组成了一个大正方形,中间还有一个小正方形.大正方形的边长是直角三角形的斜边,小正方形的边长是两直角边的差. 问题2:直角三角形的三边之间满足什么样的数量关系? 这节课我们就来探索直角三角形边长之间的奥秘.(教师板书课题:第1课时 探索勾股定理) 学生活动:观察展示的图片.进行联想、猜测. 教师可先不做评价总结,让学生带着这些猜测进行下面的学习,进行验证. 2.观察探究,学习新知 【过渡语】直角三角形的三边具有特殊的关系,刻画这种关系的命题就是著名的勾股定理. 活动一:一起探究——勾股定理 探究1:探索边长为3,4,5的直角三角形的情况 如图所示,每个小正方形都是边长为1的小正方形,在所围成的ΔABC中,∠ACB=90°.图中以AC,BC,AB为边的正方形的面积分别是多少?这三个正方形的面积之间具有怎样的关系 问题: (1)以AC为边的正方形的面积是 ; (2)以BC为边的正方形的面积是 ; (3)从AB为边的正方形的面积是 ; (4)三个正方形的面积之间关系是 + = . 探究2:探索直角边长为1的等腰直角三角形 如图所示的是用大小相同的两种颜色的正方形地砖铺成的地面示意图,∠ACB=90°.分别以AC,BC,AB为边的三个正方形(粗线标出)的面积之间有怎样的关系 学生观察发现:以AC,BC为边的正方形的面积都是1. 说明:对于以AB为边的正方形的面积,教师可让学生通过数格子的方法求出其面积,也可以将其分成四个等腰直角三角形的面积来求. 探究3:类比发现,形成结论 如图所示,在ΔABC中,∠ACB=90°,请你猜想:分别以AC,BC,AB为边的三个正方形的面积之间是否也具有上述我们探究的面积之间的关系?若具有这种关系,请用图中的RtΔABC的边把这种关系表示出来. 学生思考、交流,教师请学生口答,并板书. 教师总结:在直角三角形中,两条直角边的平方和等于斜边的平方. 活动二:试着做做——总结勾股定理 如图是用四个全等的直角三角形拼成的,其中,四边形ABDE和四边形CFGH都是正方形.请你根据此图,利用它们之 间的面积关系推导出:a2 +b2=c2. 推导过程: S大正方形=c2,S小正方形=(b-a)2, ∴ S大正方形=4·S三角形+S小正方形, 即c2=4×ab+(b-a)2=a2+b2. 【总结】 如图,我国古代把直角三角形较短的直角边叫做“勾”,较长的直角边叫做“股”,斜边叫做“弦”.因此,直角三角形三边之间的关系称为勾股定理 . 勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2. 勾股定理也可叙述为:直角三角形两直角边的平方和等于斜边的平方. 【拓展】设三角形三边长分别为a,b,c,且c为最大边长: 在钝角三角形中,有a2+b2<c2; 在锐角三角形中,有a2+b2>c2. 活动三:做一做——验证勾股定理 请比较下图(1)和(2)的两个正方形的面积,验证勾股定理. 学生动手验证,根据面积法验证. 3.学以致用,应用新知 考点1 勾股定理 【例1】 若一个直角三角形的两条直角边长都为1,则它的斜边长的平方是( ) A. B.1 C.2 D.4 答案:C 变式训练 【思想方法—分类讨论】若一个直角三角形的两条边长分别为3,4,则它的第三边长的平方是 . 答案:25或7 考点2 勾股定理的验证 【例2】1876年,美国总统伽菲尔德利用下图验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,验证中用到的面积相等关系是( ) A.S△EDA=S△CEB B.S△EDA+S△CEB=S△CDE C.S四边形AECD=S 四边形DEBC D.S△EDA+S△CDE+S△CEB=S四边形ABCD 答案:D 考点3 勾股定理的简单应用 【例3】如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了几步路,却踩伤了花草.他们少走的路长为( ) A.2 m B.3 m C.3.5 m D.4 m 答案:D 变式训练 如图,小明将一张长为 20 cm,宽为 15 cm 的长方形纸片(AE>DE)剪去了一角,量得 AB=3 cm,CD=4 cm,则BC的长为 cm. 答案:20 4.随堂训练,巩固新知 (1)如图,在△ABC中,∠B=90°,AB=1,BC=2,四边形ADEC是正方形,则正方形ADEC的面积是( ) A.3 B.4 C.5 D.6 答案:C (2)如图,点C是线段AB上的一点分别以AC,BC为边向两侧作正方形.设AB=6,两个正方形的面积和S1+S2=20,则图中△BCD的面积为( ) A.4 B.6 C.8 D.10 答案:A (3)利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图. 观察图形,求图中小正方形的面积. 解法1:小正方形的面积= ; 解法2:小正方形的面积= ; 由解法1和2,可以得到a,b,c之间的关系式为 . 答案:(b-a)2;c2-2ab;a2+b2=c2 (4)求下图中字母所代表的正方形面积. 解:SA=16+9=25;SB=169-25=144. (5)求出下列直角三角形中未知边的长度. 解:左图:x2=152+202=625,x=25; 右图:y2=132-52=144,y=12. (6)如图,一高为5米的竹竿,靠在高为4米的墙上,这时竹竿底部与墙的距离是多少 解:在Rt△ABC中,根据勾股定理, 得BC2=AB2-AC2=52-42=9, 所以BC=3. 所以梯脚与墙的距离是3米.. 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方. (3)勾股定理的变形公式:a=,b=,c=. 要求直角三角形中某一边的长度,就要知道其他两边的长度. 6.布置作业 课本P152练习1-2题,P152-153习题A,B组. 教师通过学生有趣的图片引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透爱国主义教育,同时也激发了学生的学习兴趣,加强了非智力因素的培养. 整个探究活动以从特殊到一般的的思想方法进行,让学生从对勾股定理的感性认识提升为理性认识. 探究过程以学生的观察、发现、小组讨论为主,充分体现了学生的主体地位及教师的辅助作用. 得到结论时,可以让学生尝试用数学语言表达该结论. 利用面积法对勾股定理进行验证,充分调动学生积极性,充分思考并理解面积法验证勾股定理. 通过例题讲解,巩固学生对勾股定理及验证的理解,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
板书设计 17.3 勾股定理 第1课时 勾股定理 提纲掣领,重点突出.
教后反思 1.本节课始终贯彻以学生为主体为理念,充分运用各种手段调动学生参与探索活动的积极性.在探求直角三角形三边平方关系的时候,遵循了发现问题、证实问题到推导问题的认知过程.勾股定理作为“千古第一定理”,也是我国数学家的光芒之一,可增加学生的家国情怀和自豪感. 2.在进行勾股定理结论探索的时候,一定要立足于“面积相等”这个探究的核心点,这样才能保证学生找准探索活动的方向. 反思,更进一步提升.
第1课时 勾股定理
课题 第1课时 勾股定理 课型 新授课
教学内容 教材第150-152页的内容
教学目标 1.经历探索勾股定理的过程,发展对图形性质或数量关系猜想的能力,体会拼图验证的合理性. 2.掌握勾股定理. 3.在探索的过程中,体会数形结合、由特殊到一般及化归等数学思想方法.
教学重难点 教学重点:勾股定理的探索过程. 教学难点:勾股定理的简单运用.
教 学 过 程 备 注
1.创设情境,引入课题 2002年第24届世界数学家大会在我国北京召开,图片显示的是本届世界数学家大会的会标: 问题1:观察会标,这个图案是由哪些基本图形组成? 学生:这个图形由四个全等的直角三角形组成了一个大正方形,中间还有一个小正方形.大正方形的边长是直角三角形的斜边,小正方形的边长是两直角边的差. 问题2:直角三角形的三边之间满足什么样的数量关系? 这节课我们就来探索直角三角形边长之间的奥秘.(教师板书课题:第1课时 探索勾股定理) 学生活动:观察展示的图片.进行联想、猜测. 教师可先不做评价总结,让学生带着这些猜测进行下面的学习,进行验证. 2.观察探究,学习新知 【过渡语】直角三角形的三边具有特殊的关系,刻画这种关系的命题就是著名的勾股定理. 活动一:一起探究——勾股定理 探究1:探索边长为3,4,5的直角三角形的情况 如图所示,每个小正方形都是边长为1的小正方形,在所围成的ΔABC中,∠ACB=90°.图中以AC,BC,AB为边的正方形的面积分别是多少?这三个正方形的面积之间具有怎样的关系 问题: (1)以AC为边的正方形的面积是 ; (2)以BC为边的正方形的面积是 ; (3)从AB为边的正方形的面积是 ; (4)三个正方形的面积之间关系是 + = . 探究2:探索直角边长为1的等腰直角三角形 如图所示的是用大小相同的两种颜色的正方形地砖铺成的地面示意图,∠ACB=90°.分别以AC,BC,AB为边的三个正方形(粗线标出)的面积之间有怎样的关系 学生观察发现:以AC,BC为边的正方形的面积都是1. 说明:对于以AB为边的正方形的面积,教师可让学生通过数格子的方法求出其面积,也可以将其分成四个等腰直角三角形的面积来求. 探究3:类比发现,形成结论 如图所示,在ΔABC中,∠ACB=90°,请你猜想:分别以AC,BC,AB为边的三个正方形的面积之间是否也具有上述我们探究的面积之间的关系?若具有这种关系,请用图中的RtΔABC的边把这种关系表示出来. 学生思考、交流,教师请学生口答,并板书. 教师总结:在直角三角形中,两条直角边的平方和等于斜边的平方. 活动二:试着做做——总结勾股定理 如图是用四个全等的直角三角形拼成的,其中,四边形ABDE和四边形CFGH都是正方形.请你根据此图,利用它们之 间的面积关系推导出:a2 +b2=c2. 推导过程: S大正方形=c2,S小正方形=(b-a)2, ∴ S大正方形=4·S三角形+S小正方形, 即c2=4×ab+(b-a)2=a2+b2. 【总结】 如图,我国古代把直角三角形较短的直角边叫做“勾”,较长的直角边叫做“股”,斜边叫做“弦”.因此,直角三角形三边之间的关系称为勾股定理 . 勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2. 勾股定理也可叙述为:直角三角形两直角边的平方和等于斜边的平方. 【拓展】设三角形三边长分别为a,b,c,且c为最大边长: 在钝角三角形中,有a2+b2<c2; 在锐角三角形中,有a2+b2>c2. 活动三:做一做——验证勾股定理 请比较下图(1)和(2)的两个正方形的面积,验证勾股定理. 学生动手验证,根据面积法验证. 3.学以致用,应用新知 考点1 勾股定理 【例1】 若一个直角三角形的两条直角边长都为1,则它的斜边长的平方是( ) A. B.1 C.2 D.4 答案:C 变式训练 【思想方法—分类讨论】若一个直角三角形的两条边长分别为3,4,则它的第三边长的平方是 . 答案:25或7 考点2 勾股定理的验证 【例2】1876年,美国总统伽菲尔德利用下图验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,验证中用到的面积相等关系是( ) A.S△EDA=S△CEB B.S△EDA+S△CEB=S△CDE C.S四边形AECD=S 四边形DEBC D.S△EDA+S△CDE+S△CEB=S四边形ABCD 答案:D 考点3 勾股定理的简单应用 【例3】如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了几步路,却踩伤了花草.他们少走的路长为( ) A.2 m B.3 m C.3.5 m D.4 m 答案:D 变式训练 如图,小明将一张长为 20 cm,宽为 15 cm 的长方形纸片(AE>DE)剪去了一角,量得 AB=3 cm,CD=4 cm,则BC的长为 cm. 答案:20 4.随堂训练,巩固新知 (1)如图,在△ABC中,∠B=90°,AB=1,BC=2,四边形ADEC是正方形,则正方形ADEC的面积是( ) A.3 B.4 C.5 D.6 答案:C (2)如图,点C是线段AB上的一点分别以AC,BC为边向两侧作正方形.设AB=6,两个正方形的面积和S1+S2=20,则图中△BCD的面积为( ) A.4 B.6 C.8 D.10 答案:A (3)利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图. 观察图形,求图中小正方形的面积. 解法1:小正方形的面积= ; 解法2:小正方形的面积= ; 由解法1和2,可以得到a,b,c之间的关系式为 . 答案:(b-a)2;c2-2ab;a2+b2=c2 (4)求下图中字母所代表的正方形面积. 解:SA=16+9=25;SB=169-25=144. (5)求出下列直角三角形中未知边的长度. 解:左图:x2=152+202=625,x=25; 右图:y2=132-52=144,y=12. (6)如图,一高为5米的竹竿,靠在高为4米的墙上,这时竹竿底部与墙的距离是多少 解:在Rt△ABC中,根据勾股定理, 得BC2=AB2-AC2=52-42=9, 所以BC=3. 所以梯脚与墙的距离是3米.. 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2,即直角三角形两直角边的平方和等于斜边的平方. (3)勾股定理的变形公式:a=,b=,c=. 要求直角三角形中某一边的长度,就要知道其他两边的长度. 6.布置作业 课本P152练习1-2题,P152-153习题A,B组. 教师通过学生有趣的图片引出所学内容,使学生感受到数学就在我们身边,数学离不开生活,渗透爱国主义教育,同时也激发了学生的学习兴趣,加强了非智力因素的培养. 整个探究活动以从特殊到一般的的思想方法进行,让学生从对勾股定理的感性认识提升为理性认识. 探究过程以学生的观察、发现、小组讨论为主,充分体现了学生的主体地位及教师的辅助作用. 得到结论时,可以让学生尝试用数学语言表达该结论. 利用面积法对勾股定理进行验证,充分调动学生积极性,充分思考并理解面积法验证勾股定理. 通过例题讲解,巩固学生对勾股定理及验证的理解,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
板书设计 17.3 勾股定理 第1课时 勾股定理 提纲掣领,重点突出.
教后反思 1.本节课始终贯彻以学生为主体为理念,充分运用各种手段调动学生参与探索活动的积极性.在探求直角三角形三边平方关系的时候,遵循了发现问题、证实问题到推导问题的认知过程.勾股定理作为“千古第一定理”,也是我国数学家的光芒之一,可增加学生的家国情怀和自豪感. 2.在进行勾股定理结论探索的时候,一定要立足于“面积相等”这个探究的核心点,这样才能保证学生找准探索活动的方向. 反思,更进一步提升.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
