17.3 勾股定理(第2课时)教学设计(表格式)冀教版数学八年级上册
文档属性
| 名称 | 17.3 勾股定理(第2课时)教学设计(表格式)冀教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 19:48:08 | ||
图片预览


文档简介
17.3 勾股定理
第2课时 勾股定理的实际应用
课题 第2课时 勾股定理的实际应用 课型 新授课
教学内容 教材第153-155页的内容
教学目标 1. 会运用勾股定理解决简单的实际问题. 2. 学会选择适当的数学模型解决实际问题. 3. 能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
教学重难点 教学重点:能运用勾股定理解决简单实际问题. 教学难点:勾股定理的正确运用.
教 学 过 程 备 注
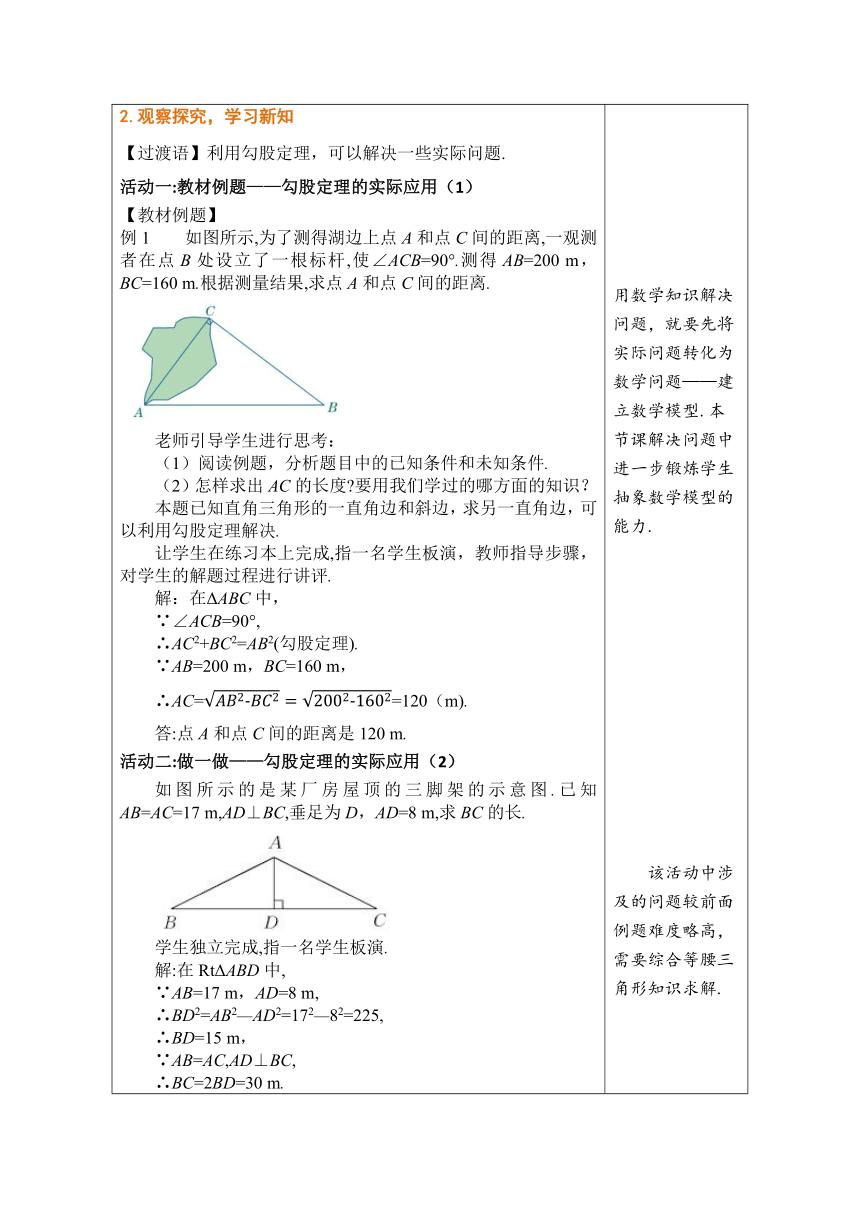
1.创设情境,引入课题 情境1:折竹抵地(源自《九章算术》): 今有竹高一丈,风折抵地,去本三尺.问折者高几何 大意:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原长竹子处3尺远.问原竹子有多高 情境2:历史上伦敦克里斯蒂拍卖行贴出了一个土地拍卖广告:如图所示,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能计算出池塘的准确面积,则池塘不计入土地价钱白白奉送.英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗 怎么解决这些问题呢?学生尝试思考解决的思路,老师适当引导. 2.观察探究,学习新知 【过渡语】利用勾股定理,可以解决一些实际问题. 活动一:教材例题——勾股定理的实际应用(1) 【教材例题】 例1 如图所示,为了测得湖边上点A和点C间的距离,一观测者在点B处设立了一根标杆,使∠ACB=90°.测得AB=200 m,BC=160 m.根据测量结果,求点A和点C间的距离. 老师引导学生进行思考: (1)阅读例题,分析题目中的已知条件和未知条件. (2)怎样求出AC的长度 要用我们学过的哪方面的知识? 本题已知直角三角形的一直角边和斜边,求另一直角边,可以利用勾股定理解决. 让学生在练习本上完成,指一名学生板演,教师指导步骤,对学生的解题过程进行讲评. 解:在ΔABC中, ∵∠ACB=90°, ∴AC2+BC2=AB2(勾股定理). ∵AB=200 m,BC=160 m, ∴AC==120(m). 答:点A和点C间的距离是120 m. 活动二:做一做——勾股定理的实际应用(2) 如图所示的是某厂房屋顶的三脚架的示意图.已知AB=AC=17 m,AD⊥BC,垂足为D,AD=8 m,求BC的长. 学生独立完成,指一名学生板演. 解:在RtΔABD中, ∵AB=17 m,AD=8 m, ∴BD2=AB2—AD2=172—82=225, ∴BD=15 m, ∵AB=AC,AD⊥BC, ∴BC=2BD=30 m. 说明:学生独立完成,有困难的小组合作完成. 活动三:教材例题——勾股定理的实际应用(3) 【教材例题】 例2 如图所示,在长为50 mm,宽为40 mm的长方形零件上有两个圆孔,与孔中心A,B相关的数据如图所示.求孔中心A和B间的距离. 先介绍图纸中所标数值的含义,再引导学生分析题意,提问: (1)在直角三角形中怎样求斜边的长度? (2)AC,BC的长度怎样求 学生独立思考交流,得出:要求斜边AB的长度,就要求出两直角边AC和BC的长度,这样就可以根据勾股定理的变形AB=求出AB的长度. 解:∵ΔABC是直角三角形, ∴AB2=AC2+BC2. ∵AC=50—15-26=9(mm), BC=40—18-10=12(mm), ∴AB==15(mm). 答:孔中心A和B间的距离是15 mm. 3.学以致用,应用新知 考点 勾股定理的实际应用 【例1】 如图,甲渔船以8海里/时的速度离开港口O向东北方向航行,乙渔船以6海里/时的速度离开港口O向西北方向航行,它们同时出发,一小时后分别到达A,B两地,此时甲、乙两渔船相距( ) A.8海里 B.10海里 C.12海里 D.13海里 答案:B 【例2】由于大风,山坡上的一棵树甲被从A点处拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的水平距离为12米,求甲树原来的高度. 解:如图所示, 过点C作CD⊥AB交AB的延长线于点D, 由题意,可得BC=13 m,DC=12 m, 在Rt△BCD中,BD2=132-122=52, 所以BD=5 m,则AD=9 m. 在Rt△ACD中,AC2=AD2+CD2=92+122=152, 所以AC=15 m,故AC+AB=15+4=19(m). 所以甲树原来的高度是19米. 4.随堂训练,巩固新知 (1)如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走( ) A.140米 B.120米 C.100米 D.90米 答案:C (2)如图,某人划船横渡一条河,由于水流的影响,实际上岸地点偏离欲到达点25 m,结果他在水中实际划了65 m,求该河流的宽度. 解:根据题中数据,由勾股定理可得, AB2=AC2-BC2=652-252=3 600, 则AB=60 m. 答:该河流的宽度是60米. (3)两棵树之间的距离为 8 m,两棵树的高度分别是 8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米? 解:根据题意画出示意图,如图所示, 两棵树的高度分别为AB=8 m,CD=2 m, 两棵树之间的距离BD=8 m, 过点C作CE⊥AB,垂足为E,连接AC. 则BE=CD=2 m,EC=BD=8 m, AE=AB-BE=8-2=6(m). 在Rt△ACE中,由勾股定理,得AC2=AE2+EC2, 即AC2=62+82=100,所以AC=10 m. 答:这只小鸟至少要飞10 m. 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)师生共同畅谈收获: 解决两点距离问题:正确画出图形,已知直角三角形两边长,利用勾股定理求第三边长. 解决折叠问题:正确画出折叠前、后的图形,运用勾股定理及方程思想解题. 解决梯子问题:梯子斜靠在墙上,梯子、墙、地面可构成直角三角形,利用勾般定理等知识解题. 6.布置作业 课本P154练习1-2题,P154-155习题A,B组. 通过情境导入,体现勾股定理在实际生活中的应用,让学生意识到数学来源于生活,又应用于生活. 也可以通过回顾上节课学过的勾股定理的知识,加深对定理的记忆与理解,为学习新课做好准备. 用数学知识解决问题,就要先将实际问题转化为数学问题——建立数学模型.本节课解决问题中进一步锻炼学生抽象数学模型的能力. 该活动中涉及的问题较前面例题难度略高,需要综合等腰三角形知识求解. 把运用勾股定理来求直角三角形的边的问题与读图、视图能力结合起来,提高学生分析问题、解决问题的能力. 通过实际问题的解答,进一步培养学生应用数学的意识,更好的促进学生对本节课重难点的理解和突破,帮助学生不断完善认知结构. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏. 归纳出本节课的知识要点,数形结合的思想方法;教师了解学生对本节课的感受并进行总结;培养学生的归纳概括能力
板书设计 17.3 勾股定理 第2课时 勾股定理的实际应用 提纲掣领,重点突出.
教后反思 本节课教师注重引导学生提炼问题的相关条件,利用小组合作学习的优势,使每个学生都得到不同程度的进步,同时发现自身存在的问题.激发学生的学习兴趣,充分地调动学生的学习积极性,给学生留有思考和探索的余地,让学生能在独立思考与合作交流中解决学习中的问题. 反思,更进一步提升.
第2课时 勾股定理的实际应用
课题 第2课时 勾股定理的实际应用 课型 新授课
教学内容 教材第153-155页的内容
教学目标 1. 会运用勾股定理解决简单的实际问题. 2. 学会选择适当的数学模型解决实际问题. 3. 能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长.
教学重难点 教学重点:能运用勾股定理解决简单实际问题. 教学难点:勾股定理的正确运用.
教 学 过 程 备 注
1.创设情境,引入课题 情境1:折竹抵地(源自《九章算术》): 今有竹高一丈,风折抵地,去本三尺.问折者高几何 大意:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原长竹子处3尺远.问原竹子有多高 情境2:历史上伦敦克里斯蒂拍卖行贴出了一个土地拍卖广告:如图所示,有面积为560英亩的土地拍卖,土地共分三个正方形,面积分别为74英亩、116英亩、370英亩.三个正方形恰好围着一个池塘,如果有人能计算出池塘的准确面积,则池塘不计入土地价钱白白奉送.英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解决吗 怎么解决这些问题呢?学生尝试思考解决的思路,老师适当引导. 2.观察探究,学习新知 【过渡语】利用勾股定理,可以解决一些实际问题. 活动一:教材例题——勾股定理的实际应用(1) 【教材例题】 例1 如图所示,为了测得湖边上点A和点C间的距离,一观测者在点B处设立了一根标杆,使∠ACB=90°.测得AB=200 m,BC=160 m.根据测量结果,求点A和点C间的距离. 老师引导学生进行思考: (1)阅读例题,分析题目中的已知条件和未知条件. (2)怎样求出AC的长度 要用我们学过的哪方面的知识? 本题已知直角三角形的一直角边和斜边,求另一直角边,可以利用勾股定理解决. 让学生在练习本上完成,指一名学生板演,教师指导步骤,对学生的解题过程进行讲评. 解:在ΔABC中, ∵∠ACB=90°, ∴AC2+BC2=AB2(勾股定理). ∵AB=200 m,BC=160 m, ∴AC==120(m). 答:点A和点C间的距离是120 m. 活动二:做一做——勾股定理的实际应用(2) 如图所示的是某厂房屋顶的三脚架的示意图.已知AB=AC=17 m,AD⊥BC,垂足为D,AD=8 m,求BC的长. 学生独立完成,指一名学生板演. 解:在RtΔABD中, ∵AB=17 m,AD=8 m, ∴BD2=AB2—AD2=172—82=225, ∴BD=15 m, ∵AB=AC,AD⊥BC, ∴BC=2BD=30 m. 说明:学生独立完成,有困难的小组合作完成. 活动三:教材例题——勾股定理的实际应用(3) 【教材例题】 例2 如图所示,在长为50 mm,宽为40 mm的长方形零件上有两个圆孔,与孔中心A,B相关的数据如图所示.求孔中心A和B间的距离. 先介绍图纸中所标数值的含义,再引导学生分析题意,提问: (1)在直角三角形中怎样求斜边的长度? (2)AC,BC的长度怎样求 学生独立思考交流,得出:要求斜边AB的长度,就要求出两直角边AC和BC的长度,这样就可以根据勾股定理的变形AB=求出AB的长度. 解:∵ΔABC是直角三角形, ∴AB2=AC2+BC2. ∵AC=50—15-26=9(mm), BC=40—18-10=12(mm), ∴AB==15(mm). 答:孔中心A和B间的距离是15 mm. 3.学以致用,应用新知 考点 勾股定理的实际应用 【例1】 如图,甲渔船以8海里/时的速度离开港口O向东北方向航行,乙渔船以6海里/时的速度离开港口O向西北方向航行,它们同时出发,一小时后分别到达A,B两地,此时甲、乙两渔船相距( ) A.8海里 B.10海里 C.12海里 D.13海里 答案:B 【例2】由于大风,山坡上的一棵树甲被从A点处拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的水平距离为12米,求甲树原来的高度. 解:如图所示, 过点C作CD⊥AB交AB的延长线于点D, 由题意,可得BC=13 m,DC=12 m, 在Rt△BCD中,BD2=132-122=52, 所以BD=5 m,则AD=9 m. 在Rt△ACD中,AC2=AD2+CD2=92+122=152, 所以AC=15 m,故AC+AB=15+4=19(m). 所以甲树原来的高度是19米. 4.随堂训练,巩固新知 (1)如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走( ) A.140米 B.120米 C.100米 D.90米 答案:C (2)如图,某人划船横渡一条河,由于水流的影响,实际上岸地点偏离欲到达点25 m,结果他在水中实际划了65 m,求该河流的宽度. 解:根据题中数据,由勾股定理可得, AB2=AC2-BC2=652-252=3 600, 则AB=60 m. 答:该河流的宽度是60米. (3)两棵树之间的距离为 8 m,两棵树的高度分别是 8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米? 解:根据题意画出示意图,如图所示, 两棵树的高度分别为AB=8 m,CD=2 m, 两棵树之间的距离BD=8 m, 过点C作CE⊥AB,垂足为E,连接AC. 则BE=CD=2 m,EC=BD=8 m, AE=AB-BE=8-2=6(m). 在Rt△ACE中,由勾股定理,得AC2=AE2+EC2, 即AC2=62+82=100,所以AC=10 m. 答:这只小鸟至少要飞10 m. 5.课堂小结,自我完善 (1)谈谈这节课你的收获有哪些? (2)师生共同畅谈收获: 解决两点距离问题:正确画出图形,已知直角三角形两边长,利用勾股定理求第三边长. 解决折叠问题:正确画出折叠前、后的图形,运用勾股定理及方程思想解题. 解决梯子问题:梯子斜靠在墙上,梯子、墙、地面可构成直角三角形,利用勾般定理等知识解题. 6.布置作业 课本P154练习1-2题,P154-155习题A,B组. 通过情境导入,体现勾股定理在实际生活中的应用,让学生意识到数学来源于生活,又应用于生活. 也可以通过回顾上节课学过的勾股定理的知识,加深对定理的记忆与理解,为学习新课做好准备. 用数学知识解决问题,就要先将实际问题转化为数学问题——建立数学模型.本节课解决问题中进一步锻炼学生抽象数学模型的能力. 该活动中涉及的问题较前面例题难度略高,需要综合等腰三角形知识求解. 把运用勾股定理来求直角三角形的边的问题与读图、视图能力结合起来,提高学生分析问题、解决问题的能力. 通过实际问题的解答,进一步培养学生应用数学的意识,更好的促进学生对本节课重难点的理解和突破,帮助学生不断完善认知结构. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏. 归纳出本节课的知识要点,数形结合的思想方法;教师了解学生对本节课的感受并进行总结;培养学生的归纳概括能力
板书设计 17.3 勾股定理 第2课时 勾股定理的实际应用 提纲掣领,重点突出.
教后反思 本节课教师注重引导学生提炼问题的相关条件,利用小组合作学习的优势,使每个学生都得到不同程度的进步,同时发现自身存在的问题.激发学生的学习兴趣,充分地调动学生的学习积极性,给学生留有思考和探索的余地,让学生能在独立思考与合作交流中解决学习中的问题. 反思,更进一步提升.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
