贵州省黔西南布依族苗族自治州兴仁县第一中学2024-2025学年高一下学期6月期末模拟考试数学试卷(含答案)
文档属性
| 名称 | 贵州省黔西南布依族苗族自治州兴仁县第一中学2024-2025学年高一下学期6月期末模拟考试数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 290.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 00:00:00 | ||
图片预览




文档简介
兴仁市第一中学2025学年高一下学期期末模拟考试数学试卷
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)已知集合A={﹣1,0,1,2},B={0,1,2,3},则A∩B=( )
A.{0,1,2} B.{1,2,3}
C.{﹣1,3} D.{﹣1,0,1,2,3}
2.(5分)已知复数,则( )
A.﹣1+3i B.﹣3+3i C.1﹣3i D.3﹣3i
3.(5分)某保密单位有两个相互独立的安全防范系统A和B,系统A和系统B在任意时刻发生故障的概率分别为和,若在任意时刻恰有一个系统发生故障的概率为( )
A. B. C. D.
4.(5分)已知a,b,c分别为△ABC三个内角A,B,C的对边,且asinC﹣ccosA=0,则A为( )
A. B. C. D.
5.(5分)小明同学计划暑假从河北省邢台市乘坐火车去河北省承德市旅游,由于没有直达的火车,小明同学有四种火车中转方案可供选择,分别是“邢台站一北京西转一承德站”“邢台站一石家庄转一承德站”“邢台站一定州转一承德站”“邢台站一保定转一承德站”,若小明同学从这四种方案中任选一种,则他到达承德站前不经北京西转的概率为( )
A. B. C. D.
6.(5分)在三棱锥P﹣ABC中,PB=PC,D,E,F分别为BC,AC,AB的中点,G为PD的中点,若EG⊥AC且EG⊥PD,则下列结论中不一定正确的是( )
A.BC∥平面EFG B.PA∥平面EFG
C.AC⊥平面EFG D.PD⊥平面EFG
7.(5分)在△ABC中,角A,B,C的对边分别是a,b,c,已知a=3,b=2,C=120°,则c=( )
A.7 B.19 C. D.
8.(5分)在△ABC中,内角A,B,C所对的边分别为a,b,c,,b=3,c=5,则a=( )
A.3 B.4 C. D.
二.多选题(共3小题,满分18分,每小题6分)
(多选)9.(6分)甲、乙两班参加某次数学调研测试,相关统计数据如下表所示(满分150分,120分以上为优秀),则下列结论正确的是( )
班级 考试人数 中位数 平均数 方差
甲 55 119 112 18
乙 56 121 112 10
A.甲、乙两班学生成绩的平均数相同
B.甲班成绩波动比乙班成绩波动大
C.甲班优秀的人数少于乙班优秀的人数
D.甲班成绩的众数小于乙班成绩的众数
(多选)10.(6分)已知向量,,,设的夹角为θ,则( )
A.⊥ B. C.∥ D.θ=135°
(多选)11.(6分)已知随机事件A,B,C,则下列说法正确的是( )
A.若P(AB)=P(A)P(B),则事件A与事件B相互独立
B.若P(A)+P(B)=1,则事件A与事件B互为对立
C.若事件A,B,C两两独立,则P(ABC)=P(A)P(B)P(C)
D.若事件A,B,C两两互斥,则P(A∪B∪C)=P(A)+P(B)+P(C)
三.填空题(共3小题,满分15分,每小题5分)
12.(5分)复数z(i为虚数单位)的共轭复数是 .
13.(5分)平面向量满足,则的最大值为 .
14.(5分)在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,三棱锥D﹣ABC为一个鳖臑,其中DA⊥平面ABC,AB⊥BC,DA=AB=BC=2,AM⊥DC,M为垂足,则三棱锥M﹣ABC的外接球的表面积为 .
四.解答题(共5小题,满分77分)
15.(13分)已知△ABC的内角A,B,C的对边分别为a,b,c,且sinA+sinC.
(1)证明:A+C=2B;
(2)记△ABC的面积为S,若S,求a+c的值.
16.(15分)设非零向量a和b,它们的夹角为θ.
(1)若||=5,θ=150°,求在上的投影的数量;
(2)若 9,||=6,求在上的投影的数量.
17.(15分)如图,正四面体(四个面都是正三角形)OABC的棱长为1,M是棱BC的中点,点N满足,点P满足.
(1)用向量表示;
(2)求.
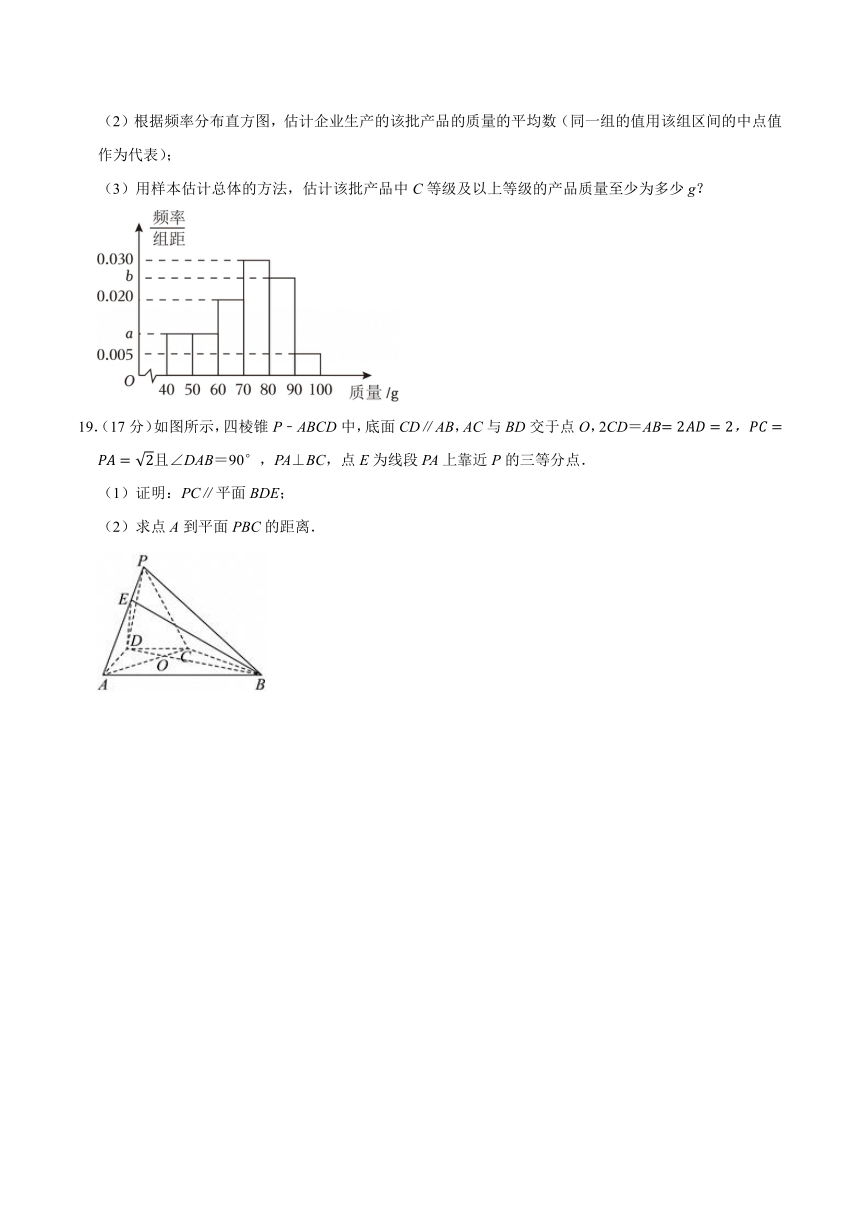
18.(17分)某企业生产某批产品按产品质量(单位:g)从高到低依比例划定A,B,C,D,E五个等级,A等级优于B等级,B等级优于C等级,C等级优于D等级,D等级优于E等级.其中A等级产品占该批产品的12%,B等级产品占该批产品的32%,C等级产品占该批产品的37%,D等级产品占该批产品的15%,E等级产品占该批产品的4%.现从该批产品中随机抽取100件产品对其质量进行分析,并绘制出如图所示的频率分布直方图,其中5a=2b.
(1)求图中a,b的值;
(2)根据频率分布直方图,估计企业生产的该批产品的质量的平均数(同一组的值用该组区间的中点值作为代表);
(3)用样本估计总体的方法,估计该批产品中C等级及以上等级的产品质量至少为多少g?
19.(17分)如图所示,四棱锥P﹣ABCD中,底面CD∥AB,AC与BD交于点O,2CD=AB且∠DAB=90°,PA⊥BC,点E为线段PA上靠近P的三等分点.
(1)证明:PC∥平面BDE;
(2)求点A到平面PBC的距离.
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C C D C C D C
二.多选题(共3小题)
题号 9 10 11
答案 ABC AD AD
12.(5分)复数z(i为虚数单位)的共轭复数是 1﹣i .
【答案】1﹣i.
解:∵z1+i,
∴复数z的共轭复数是1﹣i,
故答案为:1﹣i.
13.(5分)平面向量满足,则的最大值为 3 .
【答案】.
解:∵,∴,
则(当且仅当与同向时取等号).
故答案为:.
14.(5分)在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,三棱锥D﹣ABC为一个鳖臑,其中DA⊥平面ABC,AB⊥BC,DA=AB=BC=2,AM⊥DC,M为垂足,则三棱锥M﹣ABC的外接球的表面积为 8π .
【答案】
解:取AC的中点,连接MO,BO,则AB⊥BC,DA=AB=BC=2,
所以AC,则AO=BO=CO,
又AM⊥DC,所以MO,
所以点O就是三棱锥M﹣ABC的外接球的球心,
所以三棱锥M﹣ABC的外接球的球半径为,
所以三棱锥M﹣ABC的外接球的表面积为.
故答案为:8π.
四.解答题(共5小题,满分77分)
15.(13分)已知△ABC的内角A,B,C的对边分别为a,b,c,且sinA+sinC.
(1)证明:A+C=2B;
(2)记△ABC的面积为S,若S,求a+c的值.
【答案】(1)证明见解析;(2)8.
(1)证明:∵sinA+sinC,
∴(sinA+sinC)2=3sinAsinC+sin2B,
∴sin2A+sin2C=sinAsinC+sin2B,
∴a2+c2﹣b2=ac,
∴cosB,
又0<B<π,∴B,A+C=π﹣B,
则A+C=2B;
(2)解:∵SacsinB=4,
∴ac=16,
又S,∴b=4,
∵cosB,
∴,
∴a+c=8.
16.(15分)设非零向量a和b,它们的夹角为θ.
(1)若||=5,θ=150°,求在上的投影的数量;
(2)若 9,||=6,求在上的投影的数量.
【答案】(1);(2).
解:(1)因为||=5,θ=150°,
所以在上的投影的数量为;
(2)因为 9,||=6,
所以在上的投影的数量为.
17.(15分)如图,正四面体(四个面都是正三角形)OABC的棱长为1,M是棱BC的中点,点N满足,点P满足.
(1)用向量表示;
(2)求.
【答案】(1);
(2).
解:(1)∵M是棱BC的中点,点N满足,点P满足,
∴;
(2)∵四面体OABC是正四面体,正四面体(四个面都是正三角形)OABC的棱长为1,
∴,,
∴,同理可得,,
∴,解得.
18.(17分)某企业生产某批产品按产品质量(单位:g)从高到低依比例划定A,B,C,D,E五个等级,A等级优于B等级,B等级优于C等级,C等级优于D等级,D等级优于E等级.其中A等级产品占该批产品的12%,B等级产品占该批产品的32%,C等级产品占该批产品的37%,D等级产品占该批产品的15%,E等级产品占该批产品的4%.现从该批产品中随机抽取100件产品对其质量进行分析,并绘制出如图所示的频率分布直方图,其中5a=2b.
(1)求图中a,b的值;
(2)根据频率分布直方图,估计企业生产的该批产品的质量的平均数(同一组的值用该组区间的中点值作为代表);
(3)用样本估计总体的方法,估计该批产品中C等级及以上等级的产品质量至少为多少g?
【答案】(1)a=0.010,b=0.025;(2)71.5;(3)59.
解:(1)由题意,得,
解得a=0.010,b=0.025.
(2)企业生产的该批产品的质量的平均数约为
10×(45×0.010+55×0.010+65×0.020+75×0.030+85×0.025+95×0.005)=71.5g.
(3)等级达到C及以上的占比为12%+32%+37%=81%,
设该批产品中C等级及以上等级的产品质量至少为x g,易得50<x<60,
则(0.005+0.025+0.030+0.020)×10+(60﹣x)×0.010=0.81,
解得x=59,所以该批产品中C等级及以上等级的产品质量至少为59g.
19.(17分)如图所示,四棱锥P﹣ABCD中,底面CD∥AB,AC与BD交于点O,2CD=AB且∠DAB=90°,PA⊥BC,点E为线段PA上靠近P的三等分点.
(1)证明:PC∥平面BDE;
(2)求点A到平面PBC的距离.
【答案】(1)证明见解析;(2).
解:(1)连接OE,由于CD∥AB,所以△AOB∽△COD,且2CD=AB,
所以2CO=AO,又点E为线段PA上靠近P的三等分点,
所以,所以EO∥PC.
又OE 平面BDE,PC 平面BDE,
所以PC∥平面BDE.
(2)由题知2CD=AB=2AD=2且∠DAB=90°,CD∥AB,得,
所以∠DAC=∠DCA=∠CAB=45°,又AB=2,
所以由余弦定理得:,
所以,所以AC2+BC2=AB2,所以AC⊥BC.
PA⊥BC,PA∩AC=A,PA,AC 面PAC,
所以BC⊥面PAC,
因为PC 面PAC,
所以BC⊥PC.
又知,设A到面PBC的距离为h,
所以VB﹣PAC=VA﹣PBC,
即,
解得,
即点A到平面PBC的距离为.
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)已知集合A={﹣1,0,1,2},B={0,1,2,3},则A∩B=( )
A.{0,1,2} B.{1,2,3}
C.{﹣1,3} D.{﹣1,0,1,2,3}
2.(5分)已知复数,则( )
A.﹣1+3i B.﹣3+3i C.1﹣3i D.3﹣3i
3.(5分)某保密单位有两个相互独立的安全防范系统A和B,系统A和系统B在任意时刻发生故障的概率分别为和,若在任意时刻恰有一个系统发生故障的概率为( )
A. B. C. D.
4.(5分)已知a,b,c分别为△ABC三个内角A,B,C的对边,且asinC﹣ccosA=0,则A为( )
A. B. C. D.
5.(5分)小明同学计划暑假从河北省邢台市乘坐火车去河北省承德市旅游,由于没有直达的火车,小明同学有四种火车中转方案可供选择,分别是“邢台站一北京西转一承德站”“邢台站一石家庄转一承德站”“邢台站一定州转一承德站”“邢台站一保定转一承德站”,若小明同学从这四种方案中任选一种,则他到达承德站前不经北京西转的概率为( )
A. B. C. D.
6.(5分)在三棱锥P﹣ABC中,PB=PC,D,E,F分别为BC,AC,AB的中点,G为PD的中点,若EG⊥AC且EG⊥PD,则下列结论中不一定正确的是( )
A.BC∥平面EFG B.PA∥平面EFG
C.AC⊥平面EFG D.PD⊥平面EFG
7.(5分)在△ABC中,角A,B,C的对边分别是a,b,c,已知a=3,b=2,C=120°,则c=( )
A.7 B.19 C. D.
8.(5分)在△ABC中,内角A,B,C所对的边分别为a,b,c,,b=3,c=5,则a=( )
A.3 B.4 C. D.
二.多选题(共3小题,满分18分,每小题6分)
(多选)9.(6分)甲、乙两班参加某次数学调研测试,相关统计数据如下表所示(满分150分,120分以上为优秀),则下列结论正确的是( )
班级 考试人数 中位数 平均数 方差
甲 55 119 112 18
乙 56 121 112 10
A.甲、乙两班学生成绩的平均数相同
B.甲班成绩波动比乙班成绩波动大
C.甲班优秀的人数少于乙班优秀的人数
D.甲班成绩的众数小于乙班成绩的众数
(多选)10.(6分)已知向量,,,设的夹角为θ,则( )
A.⊥ B. C.∥ D.θ=135°
(多选)11.(6分)已知随机事件A,B,C,则下列说法正确的是( )
A.若P(AB)=P(A)P(B),则事件A与事件B相互独立
B.若P(A)+P(B)=1,则事件A与事件B互为对立
C.若事件A,B,C两两独立,则P(ABC)=P(A)P(B)P(C)
D.若事件A,B,C两两互斥,则P(A∪B∪C)=P(A)+P(B)+P(C)
三.填空题(共3小题,满分15分,每小题5分)
12.(5分)复数z(i为虚数单位)的共轭复数是 .
13.(5分)平面向量满足,则的最大值为 .
14.(5分)在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,三棱锥D﹣ABC为一个鳖臑,其中DA⊥平面ABC,AB⊥BC,DA=AB=BC=2,AM⊥DC,M为垂足,则三棱锥M﹣ABC的外接球的表面积为 .
四.解答题(共5小题,满分77分)
15.(13分)已知△ABC的内角A,B,C的对边分别为a,b,c,且sinA+sinC.
(1)证明:A+C=2B;
(2)记△ABC的面积为S,若S,求a+c的值.
16.(15分)设非零向量a和b,它们的夹角为θ.
(1)若||=5,θ=150°,求在上的投影的数量;
(2)若 9,||=6,求在上的投影的数量.
17.(15分)如图,正四面体(四个面都是正三角形)OABC的棱长为1,M是棱BC的中点,点N满足,点P满足.
(1)用向量表示;
(2)求.
18.(17分)某企业生产某批产品按产品质量(单位:g)从高到低依比例划定A,B,C,D,E五个等级,A等级优于B等级,B等级优于C等级,C等级优于D等级,D等级优于E等级.其中A等级产品占该批产品的12%,B等级产品占该批产品的32%,C等级产品占该批产品的37%,D等级产品占该批产品的15%,E等级产品占该批产品的4%.现从该批产品中随机抽取100件产品对其质量进行分析,并绘制出如图所示的频率分布直方图,其中5a=2b.
(1)求图中a,b的值;
(2)根据频率分布直方图,估计企业生产的该批产品的质量的平均数(同一组的值用该组区间的中点值作为代表);
(3)用样本估计总体的方法,估计该批产品中C等级及以上等级的产品质量至少为多少g?
19.(17分)如图所示,四棱锥P﹣ABCD中,底面CD∥AB,AC与BD交于点O,2CD=AB且∠DAB=90°,PA⊥BC,点E为线段PA上靠近P的三等分点.
(1)证明:PC∥平面BDE;
(2)求点A到平面PBC的距离.
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C C D C C D C
二.多选题(共3小题)
题号 9 10 11
答案 ABC AD AD
12.(5分)复数z(i为虚数单位)的共轭复数是 1﹣i .
【答案】1﹣i.
解:∵z1+i,
∴复数z的共轭复数是1﹣i,
故答案为:1﹣i.
13.(5分)平面向量满足,则的最大值为 3 .
【答案】.
解:∵,∴,
则(当且仅当与同向时取等号).
故答案为:.
14.(5分)在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,三棱锥D﹣ABC为一个鳖臑,其中DA⊥平面ABC,AB⊥BC,DA=AB=BC=2,AM⊥DC,M为垂足,则三棱锥M﹣ABC的外接球的表面积为 8π .
【答案】
解:取AC的中点,连接MO,BO,则AB⊥BC,DA=AB=BC=2,
所以AC,则AO=BO=CO,
又AM⊥DC,所以MO,
所以点O就是三棱锥M﹣ABC的外接球的球心,
所以三棱锥M﹣ABC的外接球的球半径为,
所以三棱锥M﹣ABC的外接球的表面积为.
故答案为:8π.
四.解答题(共5小题,满分77分)
15.(13分)已知△ABC的内角A,B,C的对边分别为a,b,c,且sinA+sinC.
(1)证明:A+C=2B;
(2)记△ABC的面积为S,若S,求a+c的值.
【答案】(1)证明见解析;(2)8.
(1)证明:∵sinA+sinC,
∴(sinA+sinC)2=3sinAsinC+sin2B,
∴sin2A+sin2C=sinAsinC+sin2B,
∴a2+c2﹣b2=ac,
∴cosB,
又0<B<π,∴B,A+C=π﹣B,
则A+C=2B;
(2)解:∵SacsinB=4,
∴ac=16,
又S,∴b=4,
∵cosB,
∴,
∴a+c=8.
16.(15分)设非零向量a和b,它们的夹角为θ.
(1)若||=5,θ=150°,求在上的投影的数量;
(2)若 9,||=6,求在上的投影的数量.
【答案】(1);(2).
解:(1)因为||=5,θ=150°,
所以在上的投影的数量为;
(2)因为 9,||=6,
所以在上的投影的数量为.
17.(15分)如图,正四面体(四个面都是正三角形)OABC的棱长为1,M是棱BC的中点,点N满足,点P满足.
(1)用向量表示;
(2)求.
【答案】(1);
(2).
解:(1)∵M是棱BC的中点,点N满足,点P满足,
∴;
(2)∵四面体OABC是正四面体,正四面体(四个面都是正三角形)OABC的棱长为1,
∴,,
∴,同理可得,,
∴,解得.
18.(17分)某企业生产某批产品按产品质量(单位:g)从高到低依比例划定A,B,C,D,E五个等级,A等级优于B等级,B等级优于C等级,C等级优于D等级,D等级优于E等级.其中A等级产品占该批产品的12%,B等级产品占该批产品的32%,C等级产品占该批产品的37%,D等级产品占该批产品的15%,E等级产品占该批产品的4%.现从该批产品中随机抽取100件产品对其质量进行分析,并绘制出如图所示的频率分布直方图,其中5a=2b.
(1)求图中a,b的值;
(2)根据频率分布直方图,估计企业生产的该批产品的质量的平均数(同一组的值用该组区间的中点值作为代表);
(3)用样本估计总体的方法,估计该批产品中C等级及以上等级的产品质量至少为多少g?
【答案】(1)a=0.010,b=0.025;(2)71.5;(3)59.
解:(1)由题意,得,
解得a=0.010,b=0.025.
(2)企业生产的该批产品的质量的平均数约为
10×(45×0.010+55×0.010+65×0.020+75×0.030+85×0.025+95×0.005)=71.5g.
(3)等级达到C及以上的占比为12%+32%+37%=81%,
设该批产品中C等级及以上等级的产品质量至少为x g,易得50<x<60,
则(0.005+0.025+0.030+0.020)×10+(60﹣x)×0.010=0.81,
解得x=59,所以该批产品中C等级及以上等级的产品质量至少为59g.
19.(17分)如图所示,四棱锥P﹣ABCD中,底面CD∥AB,AC与BD交于点O,2CD=AB且∠DAB=90°,PA⊥BC,点E为线段PA上靠近P的三等分点.
(1)证明:PC∥平面BDE;
(2)求点A到平面PBC的距离.
【答案】(1)证明见解析;(2).
解:(1)连接OE,由于CD∥AB,所以△AOB∽△COD,且2CD=AB,
所以2CO=AO,又点E为线段PA上靠近P的三等分点,
所以,所以EO∥PC.
又OE 平面BDE,PC 平面BDE,
所以PC∥平面BDE.
(2)由题知2CD=AB=2AD=2且∠DAB=90°,CD∥AB,得,
所以∠DAC=∠DCA=∠CAB=45°,又AB=2,
所以由余弦定理得:,
所以,所以AC2+BC2=AB2,所以AC⊥BC.
PA⊥BC,PA∩AC=A,PA,AC 面PAC,
所以BC⊥面PAC,
因为PC 面PAC,
所以BC⊥PC.
又知,设A到面PBC的距离为h,
所以VB﹣PAC=VA﹣PBC,
即,
解得,
即点A到平面PBC的距离为.
同课章节目录
