专题强化练6 波动图像和振动图像的综合(含答案解析)
文档属性
| 名称 | 专题强化练6 波动图像和振动图像的综合(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-23 11:28:27 | ||
图片预览


文档简介
专题强化练6 波动图像和振动图像的综合
一、选择题
1.一列简谐横波沿x轴方向传播,t=5.5 s时刻的波形图如图(a)所示,质点P的振动图像如图(b)所示,下列说法正确的是 ( )
A.这列波沿x轴负方向传播
B.这列波的波速为0.45 m/s
C.图(a)中质点P的纵坐标为6 cm
D.质点P起振后,9 s内经过的路程为60 cm
2.图甲为沿x轴传播的一列简谐横波t=0时刻的波形图,已知波源的起振方向为y轴负方向。t=0时刻在坐标原点与x=4 m之间第一次形成图甲所示波形,图乙为平衡位置在x=2 m处质点P的振动图像。则下列说法中正确的是 ( )
A.该波的波速为8 m/s
B.该波沿x轴的正方向传播
C.此时波刚好传播到x=-2 m位置
D.在t=0到t=6 s的时间内,x=-18 m处的质点通过的路程为4.8 m
3.一列简谐横波沿x轴方向传播,在t=1.25 s时的波形如图甲所示,M、N、P、Q是介质中的四个质点,已知N、Q两质点平衡位置之间的距离为16 m,图乙为质点P的振动图像。下列说法正确的是 ( )
A.该波的波速为12 cm/s
B.该波沿x轴正方向传播
C.质点P的平衡位置位于x=2 m处
D.从t=1.25 s开始,质点Q比质点P早0.25 s回到平衡位置
二、非选择题
4.图甲是一列沿x轴方向传播的简谐横波在t=1 s时刻的波形图,a是平衡位置在x=1 m处的质点,b是平衡位置在x=2 m处的质点,c是平衡位置在x=4 m处的质点,图乙为质点c的振动图像。求:
(1)该波的振幅、波速和传播方向;
(2)从t=1 s时刻起,质点a第一次到达波谷位置所经过的时间;
(3)写出b质点从t=0时刻起的振动方程。
答案与分层梯度式解析
专题强化练6 波动图像和振动图像的综合
1.D
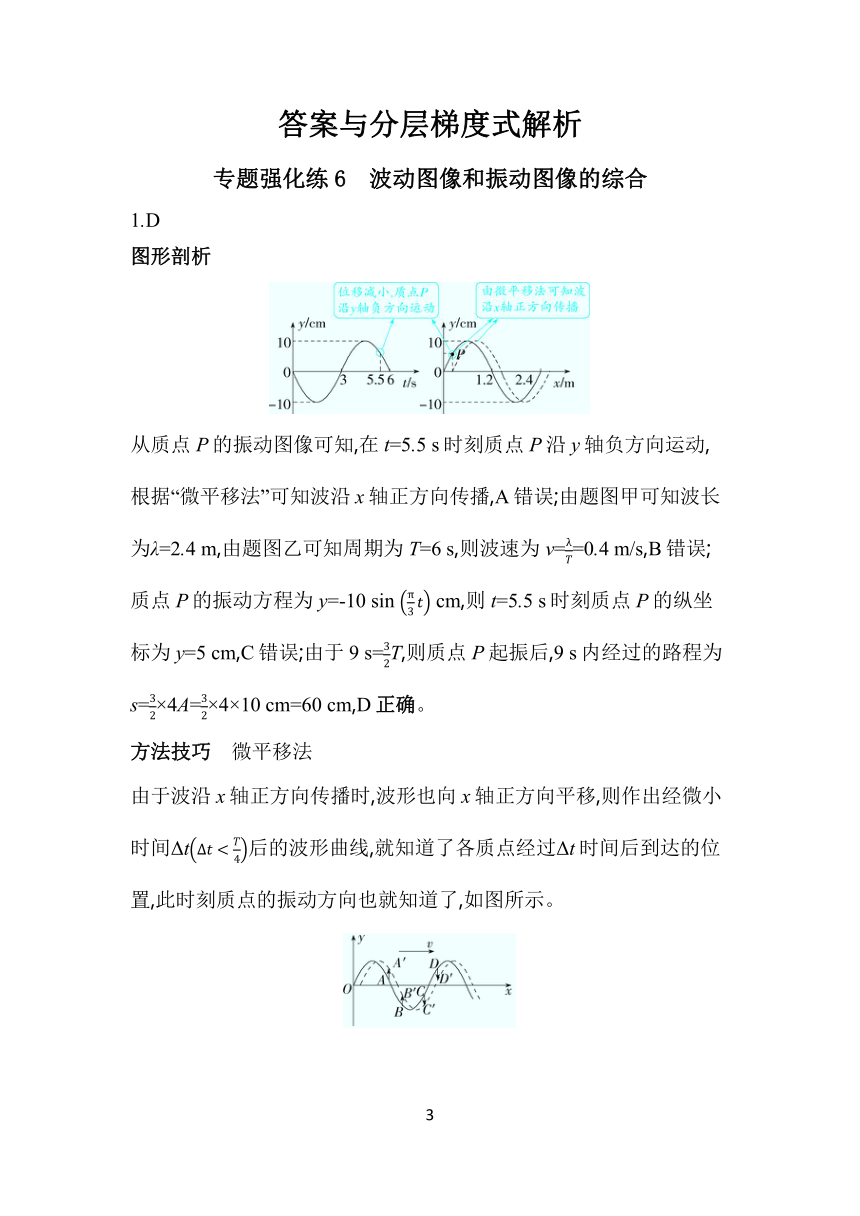
图形剖析
从质点P的振动图像可知,在t=5.5 s时刻质点P沿y轴负方向运动,根据“微平移法”可知波沿x轴正方向传播,A错误;由题图甲可知波长为λ=2.4 m,由题图乙可知周期为T=6 s,则波速为v==0.4 m/s,B错误;质点P的振动方程为y=-10 sin cm,则t=5.5 s时刻质点P的纵坐标为y=5 cm,C错误;由于9 s=T,则质点P起振后,9 s内经过的路程为s=×4A=×4×10 cm=60 cm,D正确。
方法技巧 微平移法
由于波沿x轴正方向传播时,波形也向x轴正方向平移,则作出经微小时间Δt后的波形曲线,就知道了各质点经过Δt时间后到达的位置,此时刻质点的振动方向也就知道了,如图所示。
2.C 由题图乙可得t=0时刻,质点P在平衡位置向下振动,则由题图甲可得波沿x轴的负方向传播,B错误。由于波源起振方向为y轴负方向,可得波源起振时和t=0时刻质点P振动相同,故波传播到的位置到P的距离为波长的整数倍(破题关键),又已知“坐标原点与x=4 m之间第一次形成图甲所示波形”,故波传播到的位置到P的距离为λ=4 m;结合波沿x轴负方向传播,可得此时波刚好传播到x=-2 m位置,C正确。由题图甲可得波长λ=4 m,由题图乙可得周期T=1 s,故波速为v==4 m/s,t=0时刻,波刚好传播到x=-2 m位置,那么波刚好传播到x=-18 m位置的时间为 s=4 s,故在t=0到t=6 s的时间内,x=-18 m处的质点振动的时间为2 s=2T,质点运动路程为2×4A=2×4×0.2 m=1.6 m,A、D错误。
方法技巧 振动与波的图像综合问题的分析思路
(1)确定波长λ:从波形图中可得一个完整波形的长度或相邻两个振动状态完全相同的质点之间的距离或相邻两波峰(谷)之间的距离。
(2)确定周期T:从振动图像中可得波源(或波中振动质点)完成一次全振动的时间,或由波的图像结合题设给出的波速信息由公式T=求得。
(3)根据图中信息确定波的传播方向和振动方向的关系,再结合题设条件和相应规律求解。
3.D N、Q两质点平衡位置之间的距离为xNQ=λ-λ=16 m,解得λ=24 m,根据题图乙可知波的周期为T=2 s,因此波速为v==12 m/s,A错误;由题图乙可知,t=1.25 s时刻,质点P沿y轴负方向运动,在题图甲中根据“同侧法”可知,该波沿x轴负方向传播,B错误;由题图乙可知,在t=1.25 s之后,质点P第一次位于波峰的时间为t=2.5 s,由此可知是由t=1.25 s时刻质点Q所在波峰传播来的,所以有=2.5 s-1.25 s=1.25 s,其中xQ=16 m,解得xP=1 m,故C错误;从t=1.25 s开始,质点Q第一次回到平衡位置所经历的时间为t1==0.5 s,Q点左侧波形的第一个平衡位置处坐标为x1=xQ-=10 m,该位置质点的振动状态第一次传播到P点所需时间为t2===0.75 s,则质点Q比质点P早回到平衡位置的时间为Δt=t2-t1=0.25 s,故D正确。
4.答案 (1)5 cm 4 m/s 波沿x轴负方向传播
(2)1.25 s
(3)y=5 sin cm或y=5 sin cm
解析 (1)由题图甲可知,该波的振幅为A=5 cm,波长为λ=8 m
由题图乙可知该波的周期为T=2 s
则波速为v== m/s=4 m/s
由题图乙知,t=1 s时刻,质点c由平衡位置沿y轴负方向振动;由“上下坡法”可得,题图甲中c点沿y轴负方向振动,沿传播方向看c点应处在上坡阶段,得波应沿x轴负方向传播。
(2)由于波沿x轴负方向传播,可知质点a沿y轴正方向振动,质点a第一次位于波谷位置波沿x轴负方向传播的距离x=6 m-1 m=5 m
所需的时间t== s=1.25 s
(3)在t=1 s时刻b质点位于波峰,由于波速为4 m/s,波沿x轴负方向传播,则t=0时刻b质点处于波谷。
结合简谐运动的振动方程y=A sin (ωt+φ),ω==π rad/s
由t=0时 sin φ=-1
解得φ=或φ=-
故t=0时刻起b质点的振动方程为
y=5 sin cm或y=5 sin cm
7
一、选择题
1.一列简谐横波沿x轴方向传播,t=5.5 s时刻的波形图如图(a)所示,质点P的振动图像如图(b)所示,下列说法正确的是 ( )
A.这列波沿x轴负方向传播
B.这列波的波速为0.45 m/s
C.图(a)中质点P的纵坐标为6 cm
D.质点P起振后,9 s内经过的路程为60 cm
2.图甲为沿x轴传播的一列简谐横波t=0时刻的波形图,已知波源的起振方向为y轴负方向。t=0时刻在坐标原点与x=4 m之间第一次形成图甲所示波形,图乙为平衡位置在x=2 m处质点P的振动图像。则下列说法中正确的是 ( )
A.该波的波速为8 m/s
B.该波沿x轴的正方向传播
C.此时波刚好传播到x=-2 m位置
D.在t=0到t=6 s的时间内,x=-18 m处的质点通过的路程为4.8 m
3.一列简谐横波沿x轴方向传播,在t=1.25 s时的波形如图甲所示,M、N、P、Q是介质中的四个质点,已知N、Q两质点平衡位置之间的距离为16 m,图乙为质点P的振动图像。下列说法正确的是 ( )
A.该波的波速为12 cm/s
B.该波沿x轴正方向传播
C.质点P的平衡位置位于x=2 m处
D.从t=1.25 s开始,质点Q比质点P早0.25 s回到平衡位置
二、非选择题
4.图甲是一列沿x轴方向传播的简谐横波在t=1 s时刻的波形图,a是平衡位置在x=1 m处的质点,b是平衡位置在x=2 m处的质点,c是平衡位置在x=4 m处的质点,图乙为质点c的振动图像。求:
(1)该波的振幅、波速和传播方向;
(2)从t=1 s时刻起,质点a第一次到达波谷位置所经过的时间;
(3)写出b质点从t=0时刻起的振动方程。
答案与分层梯度式解析
专题强化练6 波动图像和振动图像的综合
1.D
图形剖析
从质点P的振动图像可知,在t=5.5 s时刻质点P沿y轴负方向运动,根据“微平移法”可知波沿x轴正方向传播,A错误;由题图甲可知波长为λ=2.4 m,由题图乙可知周期为T=6 s,则波速为v==0.4 m/s,B错误;质点P的振动方程为y=-10 sin cm,则t=5.5 s时刻质点P的纵坐标为y=5 cm,C错误;由于9 s=T,则质点P起振后,9 s内经过的路程为s=×4A=×4×10 cm=60 cm,D正确。
方法技巧 微平移法
由于波沿x轴正方向传播时,波形也向x轴正方向平移,则作出经微小时间Δt后的波形曲线,就知道了各质点经过Δt时间后到达的位置,此时刻质点的振动方向也就知道了,如图所示。
2.C 由题图乙可得t=0时刻,质点P在平衡位置向下振动,则由题图甲可得波沿x轴的负方向传播,B错误。由于波源起振方向为y轴负方向,可得波源起振时和t=0时刻质点P振动相同,故波传播到的位置到P的距离为波长的整数倍(破题关键),又已知“坐标原点与x=4 m之间第一次形成图甲所示波形”,故波传播到的位置到P的距离为λ=4 m;结合波沿x轴负方向传播,可得此时波刚好传播到x=-2 m位置,C正确。由题图甲可得波长λ=4 m,由题图乙可得周期T=1 s,故波速为v==4 m/s,t=0时刻,波刚好传播到x=-2 m位置,那么波刚好传播到x=-18 m位置的时间为 s=4 s,故在t=0到t=6 s的时间内,x=-18 m处的质点振动的时间为2 s=2T,质点运动路程为2×4A=2×4×0.2 m=1.6 m,A、D错误。
方法技巧 振动与波的图像综合问题的分析思路
(1)确定波长λ:从波形图中可得一个完整波形的长度或相邻两个振动状态完全相同的质点之间的距离或相邻两波峰(谷)之间的距离。
(2)确定周期T:从振动图像中可得波源(或波中振动质点)完成一次全振动的时间,或由波的图像结合题设给出的波速信息由公式T=求得。
(3)根据图中信息确定波的传播方向和振动方向的关系,再结合题设条件和相应规律求解。
3.D N、Q两质点平衡位置之间的距离为xNQ=λ-λ=16 m,解得λ=24 m,根据题图乙可知波的周期为T=2 s,因此波速为v==12 m/s,A错误;由题图乙可知,t=1.25 s时刻,质点P沿y轴负方向运动,在题图甲中根据“同侧法”可知,该波沿x轴负方向传播,B错误;由题图乙可知,在t=1.25 s之后,质点P第一次位于波峰的时间为t=2.5 s,由此可知是由t=1.25 s时刻质点Q所在波峰传播来的,所以有=2.5 s-1.25 s=1.25 s,其中xQ=16 m,解得xP=1 m,故C错误;从t=1.25 s开始,质点Q第一次回到平衡位置所经历的时间为t1==0.5 s,Q点左侧波形的第一个平衡位置处坐标为x1=xQ-=10 m,该位置质点的振动状态第一次传播到P点所需时间为t2===0.75 s,则质点Q比质点P早回到平衡位置的时间为Δt=t2-t1=0.25 s,故D正确。
4.答案 (1)5 cm 4 m/s 波沿x轴负方向传播
(2)1.25 s
(3)y=5 sin cm或y=5 sin cm
解析 (1)由题图甲可知,该波的振幅为A=5 cm,波长为λ=8 m
由题图乙可知该波的周期为T=2 s
则波速为v== m/s=4 m/s
由题图乙知,t=1 s时刻,质点c由平衡位置沿y轴负方向振动;由“上下坡法”可得,题图甲中c点沿y轴负方向振动,沿传播方向看c点应处在上坡阶段,得波应沿x轴负方向传播。
(2)由于波沿x轴负方向传播,可知质点a沿y轴正方向振动,质点a第一次位于波谷位置波沿x轴负方向传播的距离x=6 m-1 m=5 m
所需的时间t== s=1.25 s
(3)在t=1 s时刻b质点位于波峰,由于波速为4 m/s,波沿x轴负方向传播,则t=0时刻b质点处于波谷。
结合简谐运动的振动方程y=A sin (ωt+φ),ω==π rad/s
由t=0时 sin φ=-1
解得φ=或φ=-
故t=0时刻起b质点的振动方程为
y=5 sin cm或y=5 sin cm
7
