第三章 机械波 增分测评卷(含答案解析)
文档属性
| 名称 | 第三章 机械波 增分测评卷(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 383.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-23 11:42:48 | ||
图片预览


文档简介
(
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第三章 机械波
注意事项
1.本试卷满分100分,考试用时90分钟。
2.无特殊说明,本试卷中重力加速度g取10 m/s2。
一、选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项符合题目要求)
1.如图所示,P为桥墩,A为靠近桥墩浮在水面的树叶,波源S连续振动形成水波,此时树叶几乎不动。为使水波能带动树叶明显振动,可采用的方法是 ( )
A.减小波源的振幅
B.减小波源距桥墩的距离
C.增大波源的频率
D.减小波源的频率
2.如图所示,学生在玩“人浪”游戏。学生手挽手排成一行,从左边第一位同学开始,周期性地“下蹲、起立”,呈现类似波浪的效果。则 ( )
A.“人浪”是纵波
B.“人浪”传播的是“下蹲、起立”这种运动形式
C.当“人浪”向右传播时,学生随“人浪”向右移动
D.学生“下蹲、起立”的动作越频繁,“人浪”传播的速度一定越快
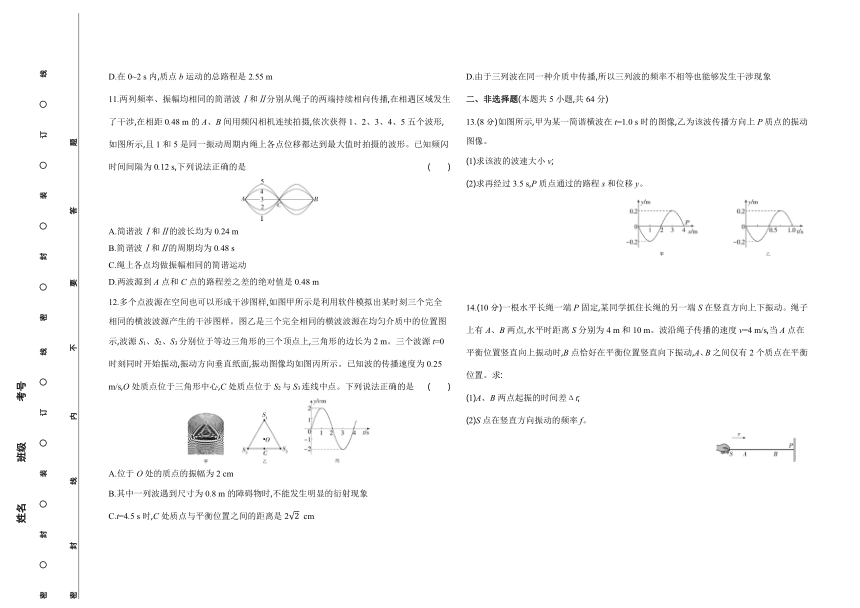
3.某同学在研究机械波的形成与传播规律时,将一根粗细均匀的弹性绳右端固定在墙上。手握着绳子左端S点上下振动,产生向右传播的绳波,某时刻的波形如图所示。下列说法中正确的是 ( )
A.此时刻质点P向上运动 B.S点的起振方向向上
C.手振动的频率逐渐增大 D.波的传播速度不变
4.汽车主动降噪系统是一种能够自动减少车内噪声的技术,在汽车行驶过程中,许多因素都会产生噪声,系统会通过车身的声学反馈技术,通过扬声器发出声波将车外噪声反向抵消,从而减少车内噪声。某一稳定噪声信号的振动方程为y=A sin ,下列说法正确的是 ( )
A.抵消声波频率应为100 Hz
B.抵消声波振幅应为2A
C.汽车降噪过程应用的是声波的多普勒效应
D.抵消声波和环境噪声在空气中传播的速度大小相等
5.位于坐标原点处的波源发出一列沿x轴正方向传播的简谐横波。t=0时波源开始振动,其位移y随时间t变化的关系式为y=A sin t,则t=T时的波形图为 ( )
6.两列完全相同的机械波在某时刻的叠加情况如图所示,图中的实线和虚线分别表示波峰和波谷,此时 ( )
A.a、b连线中点振动减弱
B.a、b连线中点速度为0
C.a、b、c、d四点速度均为0
D.再经过周期c、d两点振动加强
7.据中国地震台网正式测定,8月23日18时19分在辽宁大连市普兰店区发生4.6级地震,震源深度8公里,震中位于北纬39.42度,东经122.20度。“地震预警”是指在地震发生以后,抢在地震波传播到受灾地区前,向受灾地区提前几秒至数十秒发出警报,通知目标区域,从而实现预警。科研机构对波的特性展开研究,如图甲所示为研究过程中简谐波t=0时刻的波形图,M是此波上的一个质点,平衡位置处于x=4 m处,图乙为质点M的振动图像,则 ( )
A.该列波沿x轴正方向传播
B.该列波的传播速度为4 m/s
C.质点M在7 s内通过的路程为280 cm
D.质点M在2 s内沿x轴运动了8 m
8.一列简谐横波沿x轴传播,t=0时刻的波形图如图所示。P、Q是波传播路径上的两个质点,t=0时刻,质点Q正向平衡位置运动,质点P的振动频率与摆长为0.25 m的单摆振动频率相同,取重力加速度g=π2 m/s2,则下列说法不正确的是 ( )
A.该波沿x轴正方向传播
B.该波的传播速度为0.4 m/s
C.质点Q在0~1.5 s内通过的路程为30 cm
D.质点P的振动方程为y=-5 sin 2πt cm
9.如图所示,一列沿x轴正方向传播的简谐横波,实线是t=0时刻的波形图,虚线是这列波经Δt=1.1 s的波形图,T<Δt<2T,则下列说法正确的是 ( )
A.这列波的波长是9 cm
B.这列波的周期是0.5 s
C.这列波的波速是10 m/s
D.从t=0时刻开始,x=5 cm处的质点经0.35 s振动到波峰
10.位于x=0.25 m的波源p从t=0时刻开始振动,形成的简谐横波沿x轴正负方向传播,在t=2.0 s时波源停止振动,t=2.1 s时的部分波形如图所示,其中质点a的平衡位置xa=1.75 m,质点b的平衡位置xb=-0.5 m。下列说法正确的是 ( )
A.沿x轴正负方向传播的波发生干涉
B.t=0.42 s时,波源的位移为负
C.t=2.25 s时,质点a沿y轴负方向振动
D.在0~2 s内,质点b运动的总路程是2.55 m
11.两列频率、振幅均相同的简谐波Ⅰ和Ⅱ分别从绳子的两端持续相向传播,在相遇区域发生了干涉,在相距0.48 m的A、B间用频闪相机连续拍摄,依次获得1、2、3、4、5五个波形,如图所示,且1和5是同一振动周期内绳上各点位移都达到最大值时拍摄的波形。已知频闪时间间隔为0.12 s,下列说法正确的是 ( )
A.简谐波Ⅰ和Ⅱ的波长均为0.24 m
B.简谐波Ⅰ和Ⅱ的周期均为0.48 s
C.绳上各点均做振幅相同的简谐运动
D.两波源到A点和C点的路程差之差的绝对值是0.48 m
12.多个点波源在空间也可以形成干涉图样,如图甲所示是利用软件模拟出某时刻三个完全相同的横波波源产生的干涉图样。图乙是三个完全相同的横波波源在均匀介质中的位置图示,波源S1、S2、S3分别位于等边三角形的三个顶点上,三角形的边长为2 m。三个波源t=0时刻同时开始振动,振动方向垂直纸面,振动图像均如图丙所示。已知波的传播速度为0.25 m/s,O处质点位于三角形中心,C处质点位于S2与S3连线中点。下列说法正确的是 ( )
A.位于O处的质点的振幅为2 cm
B.其中一列波遇到尺寸为0.8 m的障碍物时,不能发生明显的衍射现象
C.t=4.5 s时,C处质点与平衡位置之间的距离是2 cm
D.由于三列波在同一种介质中传播,所以三列波的频率不相等也能够发生干涉现象
二、非选择题(本题共5小题,共64分)
13.(8分)如图所示,甲为某一简谐横波在t=1.0 s时的图像,乙为该波传播方向上P质点的振动图像。
(1)求该波的波速大小v;
(2)求再经过3.5 s,P质点通过的路程s和位移y。
14.(10分)一根水平长绳一端P固定,某同学抓住长绳的另一端S在竖直方向上下振动。绳子上有A、B两点,水平时距离S分别为4 m和10 m。波沿绳子传播的速度v=4 m/s,当A点在平衡位置竖直向上振动时,B点恰好在平衡位置竖直向下振动,A、B之间仅有2个质点在平衡位置。求:
(1)A、B两点起振的时间差Δt;
(2)S点在竖直方向振动的频率f。
15.(14分)如图所示,一根张紧的水平弹性长绳上的a、b两点相距L=12.0 m,b点在a点的右方。一列简谐横波沿此长绳向右传播。在t=0时刻,a点的位移ya=4 cm(4 cm为质点振动的振幅),b点的位移yb=0,且向下运动,T=2 s。
(1)求质点a的振动方程;
(2)若这一列简谐波的波长λ16.(14分)一振动片做简谐运动时,振动图像如图甲所示。固定在振动片上的两根细杆同步周期性地触动水面上的a、b两点,两波源发出的波在水面上形成稳定的干涉图样。c点是以ab为直径的半圆弧上的一点,且圆心O与c点的连线垂直于ab,如图乙所示,圆弧的半径为R。已知除c点外,圆弧上还有其他振幅极大的点,其中d点是离c点最近的振幅极大的点,∠dOc=30°。
(1)求波的波长λ;
(2)求波的传播速度v;
(3)圆弧上还有几个振幅始终为零的点,其中e点(图中未画出)是与d点相邻的振幅为零的点,求线段be与ae的差。
17.(18分)水面上水波的传播速度跟水的深度有关,其关系式为v=,式中h为水的深度,g为重力加速度。如图甲所示是某水域的剖面图,C、D两部分深度不同,图乙是俯视示意图,O点处于两部分水面分界线上,M和N分别是处在C和D两区域水面上的点。t=0时刻O点从平衡位置向上振动,形成以O点为波源向左和向右传播的水波(可看作是简谐横波)。t=2.5 s时O点第二次到达波峰,此时M点第一次到达波峰。已知D区域水波振幅A=5 cm,水深hD=0.90 m,O、M间距离4.0 m,O、N间距离3.0 m。求:
(1)C区域的水深hC;
(2)N点在t=3 s时的振动方向及此时的位移;
(3)t=10 s时,处在D区域水面上的Q点(图中未标出)处于波峰,且O、Q间只有一个波峰,则Q点在t=0至t=10 s时间内振动的路程是多少
答案全解全析
1.D 根据题意,为使水波能带动树叶明显振动,即发生明显衍射现象,应减小障碍物的尺寸或者增大波长,根据λ=可知,减小波源的频率,波长增大,选项C错误,D正确;减小波源的振幅、减小波源距桥墩的距离对波长无影响,选项A、B错误。
2.B 振动方向与传播方向垂直,则“人浪”是横波,A错误;“人浪”只传播“下蹲、起立”这种运动形式,学生不会随波移动,B正确,C错误;“人浪”传播速度的快慢与人“下蹲、起立”的动作频繁程度无直接关系,D错误。
3.D 波向右传播,由带动法可知,此时刻质点P向下运动,A错误;此时,右侧刚开始运动的质点向下运动,则波源的起振方向向下,B错误;由图可知,波长逐渐增大,而波速由介质决定,波速不变,根据λ=vT,则周期逐渐增大,频率逐渐减小,C错误,D正确。
4.D 汽车降噪过程应用的是声波的叠加原理,抵消声波的振幅和频率应与环境噪声的振幅和频率相同,则抵消声波的振幅为A,频率应为f== Hz=50 Hz,故A、B、C错误;波速由介质决定,抵消声波和环境噪声在空气中传播的速度大小相等,D正确。
5.D t=0时波源开始振动,由波源振动方程可知,波源从平衡位置开始振动,起振方向沿y轴正方向,而波传播方向上各质点的起振方向与波源均相同,故t=T时,波向x轴正方向传播的距离为一个波长,且最右侧质点位于平衡位置,振动方向沿y轴正方向,根据“上下坡法”可知t=T时的波形图为D。
6.C a点是波谷与波谷相遇点,b点是波峰与波峰相遇点,c、d两点是波峰与波谷相遇点,则a、b两点是振动加强的,且a、b连线上的点也是振动加强的,c、d两点是振动减弱的;a、b两点连线中点未到达波峰或波谷,故速度不为0,选项A、B错误。a处于波谷,速度为零;b处于波峰,速度为零;c、d两点波峰与波谷相遇,速度为零,即四点的速度均为0,选项C正确;再经过周期c、d两点振动仍然减弱,选项D错误。
7.C 根据题图乙可知,平衡位置处于x=4 m处的质点M在t=0时沿着y轴正方向振动,则由“同侧法”可知,该列波沿x轴负方向传播,A错误;波的波长λ=4 m,周期T=2 s,则该列波的传播速度为v==2 m/s,B错误;由于7 s=3T,则质点M通过的路程为s=3×4A=14×20 cm=280 cm,C正确;质点只在平衡位置附近上下振动,并不会随波迁移,D错误。
8.D t=0时刻,质点Q正向平衡位置运动,根据“上下坡法”可以判断该波沿x轴正方向传播,A说法正确;摆长为0.25 m的单摆的振动频率f== =1 Hz,因此该波的周期T==1 s,由题图可知该波的波长为0.4 m,故波传播的速度为v==0.4 m/s,故B说法正确;由于波的周期为1 s,1.5 s=1.5T,所以质点Q在1.5 s内通过的路程为s=6A=30 cm,C说法正确;质点P振动的圆频率为ω==2π rad/s,t=0时刻质点P从平衡位置向y轴正方向振动,故振动方程为y=A sin ωt=5 sin 2πt cm,故D错误。
9.D 由波形图可知,这列波的波长λ=6 cm,A错误;由于波沿x轴正方向传播,且T<Δt<2T,故由图像可知,Δt=1.1 s内波传播的距离Δx=λ+λ=λ=11 cm,则Δt=T=1.1 s,故波的周期T=0.6 s,B错误;这列波的波速v===10 cm/s,C错误;t=0时刻x1=1.5 cm处的质点位于波峰,从t=0时刻开始,该波峰第一次传播到x=5 cm处,经历的时间t===0.35 s,D正确。
10.D 波从波源发出后,向x轴正、负方向传播即向相反方向传播,波不会相遇,故不会发生干涉,A错误。由题图可知,波的波长λ=1 m,0.1 s内波传播四分之一波长,可得=0.1 s,解得T=0.4 s;根据“同侧法”可知,波源的起振方向向上,根据周期性并结合波的图像可知,t=0.42 s即T0.25 s,故t=2.25 s时质点a还在继续振动,t=2.1 s到t=2.25 s波传播的距离为x=vt2=2.5×0.15 m=0.375 m,即沿x轴正方向传播的波由题图中位置向右平移0.375 m,结合图像可知质点a的位移为正且向y轴正方向运动,C错误;波源的振动传到b点所需的时间t3= s=0.3 s,在0~2 s内,质点b振动的时间为t4=2 s-0.3 s=1.7 s=T,质点b运动的总路程s=×4A=17×0.15 m=2.55 m,D正确。
11.D 由图知,简谐波Ⅰ和Ⅱ的波长均为0.48 m,A错误;1和5是同一振动周期内绳上各点位移都达到最大值时拍摄的波形,相差半个周期,故简谐波Ⅰ和Ⅱ的周期均为0.96 s,B错误;图中除A、C、B三点为振动减弱点,振幅为零外,其他各点振幅不为零,故C错误;A、C是相邻的振动减弱点,两波源到A点和C点的路程差之差的绝对值等于波长0.48 m,D正确。
12.C O点位于正三角形的中心,该点到三个波源的距离相等,可知O处质点为振动加强点,则该点的振幅为3A=3×2 cm=6 cm,A错误。根据题图丙可知,该波的周期为4 s,根据波速公式v=,可得λ=1 m>0.8 m,根据发生明显衍射的条件可知,波遇到尺寸为0.8 m的障碍物时,能发生明显的衍射现象,B错误。根据几何关系可知S1C=S1S2 sin 60°= m,则波源S1的振动传播到C所需要时间t1==4 s>4.5 s,可知t=4.5 s时,波源S1的振动还没有传播到C点;波源S2与S3的振动传播到C所需要的时间均为t2= s=4 s<4.5 s,可知t=4.5 s时,波源S2与S3的振动传播到了C点,由于S2C=S3C=1 m=λ,4.5 s=T+,C处质点为振动加强点,表明C处质点4.5 s时刻的位移为波源S2与S3在时刻位移的叠加;图丙的振动方程为y=2 sin t (cm)=2 sin t (cm),当t=时,解得y0= cm,则t=4.5 s时,C处质点与平衡位置之间的距离是2y0=2 cm,C正确。根据发生干涉的条件可知,机械波要发生干涉,波的频率必须相等,即三列波的频率不相等不能够发生干涉现象,D错误。
13.答案 (1)4 m/s (2)2.8 m 0
解析 (1)由题图甲可得,该波的波长λ=4 m(1分)
由题图乙可得周期T=1 s(1分)
所以波速v==4 m/s(2分)
(2)由于3.5 s=7× (1分)
所以经过3.5 s质点通过的路程s=7×2A=2.8 m(1分)
由于波动具有重复性,经历时间为3.5个周期,P质点又回到图示位置,其位移为0 (2分)
14.答案 (1)1.5 s (2)1 Hz
解析 (1)波在介质中匀速传播,根据x=vt (2分)
可得A、B两点起振的时间差为Δt== s=1.5 s(2分)
(2)根据题意可画出A、B两点间的波形,如图所示 (2分)
可知xB-xA=1.5λ=6 m(1分)
解得λ=4 m(1分)
根据波速公式v=λf (1分)
解得振动的频率f=1 Hz(1分)
15.答案 (1)ya=4 sin cm(或ya=4 cos πt cm) (2) m/s(n=1,2,3,…)
解析 (1)设质点a的振动方程为ya=A sin (1分)
根据题意可得A=4 cm,T=2 s(1分)
可得ya=4 sin (πt+φ) cm(1分)
由t=0时刻,a点的位移ya=4 cm,可知4 cm=4 sin φ cm(1分)
解得φ= (1分)
则质点a的振动方程为ya=4 sin cm=4 cos πt cm(2分)
(2)当a、b两点间的距离小于波长时,波形如图所示 (1分)
根据题意有L=λ+nλ(n=0,1,2,3,…) (1分)
又已知λ解得λ= m(n=1,2,3,…) (2分)
根据v=解得v= m/s(n=1,2,3,…) (2分)
16.答案 (1)(-1)R (2) (3)见解析
解析 (1)连接a、d,b、d,由几何关系可知∠dOa=60°,∠dba=30° (1分)
则ad=R (1分)
bd=R (1分)
d点是离c点最近的振幅极大的点,即振动加强点,有bd-ad=λ (2分)
所以波的波长λ=(-1)R (1分)
(2)由题图甲可知,波的周期T=2t0 (1分)
所以波的传播速度v== (2分)
(3)由题意可知,e点为振动减弱点,到两波源的距离之差等于半波长的奇数倍。 (1分)
若e点在圆弧上c、d之间,则有be-ae== (2分)
若e点在圆弧上a、d之间,则有be-ae== (2分)
17.答案 (1)0.40 m (2)向上振动 位移为0 (3)0.65 m
解析 (1)设波源O振动的周期为T,则有2.5 s=T (1分)
解得T=2 s(1分)
对M点的振动分析,知C区域水波波长为λC=OM=4 m(1分)
则有vC==2 m/s(1分)
根据v=求得hC=0.40 m(1分)
(2)由于D区域水深hD=0.90 m,由v= (1分)
可得D区域水波的传播速度vD==3 m/s(1分)
又由vD=解得波长λD=vDT=6 m(1分)
波传到N点所用的时间t1==1 s(1分)
所以t=3 s时,N点刚好完成一次全振动,可知其在平衡位置向上振动,位移为0。 (1分)
(3)t=10 s时,O点在平衡位置向上振动,可画出D区域水波的波动图像如图所示 (2分)
由图可知OQ=10.5 m(1分)
则有Δt== s=3.5 s(1分)
则Q点振动的时间为t2=10 s-3.5 s=6.5 s=3T (2分)
所以Q点振动的路程为s=3×4A=13A=0.65 m(2分)
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第三章 机械波
注意事项
1.本试卷满分100分,考试用时90分钟。
2.无特殊说明,本试卷中重力加速度g取10 m/s2。
一、选择题(本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项符合题目要求)
1.如图所示,P为桥墩,A为靠近桥墩浮在水面的树叶,波源S连续振动形成水波,此时树叶几乎不动。为使水波能带动树叶明显振动,可采用的方法是 ( )
A.减小波源的振幅
B.减小波源距桥墩的距离
C.增大波源的频率
D.减小波源的频率
2.如图所示,学生在玩“人浪”游戏。学生手挽手排成一行,从左边第一位同学开始,周期性地“下蹲、起立”,呈现类似波浪的效果。则 ( )
A.“人浪”是纵波
B.“人浪”传播的是“下蹲、起立”这种运动形式
C.当“人浪”向右传播时,学生随“人浪”向右移动
D.学生“下蹲、起立”的动作越频繁,“人浪”传播的速度一定越快
3.某同学在研究机械波的形成与传播规律时,将一根粗细均匀的弹性绳右端固定在墙上。手握着绳子左端S点上下振动,产生向右传播的绳波,某时刻的波形如图所示。下列说法中正确的是 ( )
A.此时刻质点P向上运动 B.S点的起振方向向上
C.手振动的频率逐渐增大 D.波的传播速度不变
4.汽车主动降噪系统是一种能够自动减少车内噪声的技术,在汽车行驶过程中,许多因素都会产生噪声,系统会通过车身的声学反馈技术,通过扬声器发出声波将车外噪声反向抵消,从而减少车内噪声。某一稳定噪声信号的振动方程为y=A sin ,下列说法正确的是 ( )
A.抵消声波频率应为100 Hz
B.抵消声波振幅应为2A
C.汽车降噪过程应用的是声波的多普勒效应
D.抵消声波和环境噪声在空气中传播的速度大小相等
5.位于坐标原点处的波源发出一列沿x轴正方向传播的简谐横波。t=0时波源开始振动,其位移y随时间t变化的关系式为y=A sin t,则t=T时的波形图为 ( )
6.两列完全相同的机械波在某时刻的叠加情况如图所示,图中的实线和虚线分别表示波峰和波谷,此时 ( )
A.a、b连线中点振动减弱
B.a、b连线中点速度为0
C.a、b、c、d四点速度均为0
D.再经过周期c、d两点振动加强
7.据中国地震台网正式测定,8月23日18时19分在辽宁大连市普兰店区发生4.6级地震,震源深度8公里,震中位于北纬39.42度,东经122.20度。“地震预警”是指在地震发生以后,抢在地震波传播到受灾地区前,向受灾地区提前几秒至数十秒发出警报,通知目标区域,从而实现预警。科研机构对波的特性展开研究,如图甲所示为研究过程中简谐波t=0时刻的波形图,M是此波上的一个质点,平衡位置处于x=4 m处,图乙为质点M的振动图像,则 ( )
A.该列波沿x轴正方向传播
B.该列波的传播速度为4 m/s
C.质点M在7 s内通过的路程为280 cm
D.质点M在2 s内沿x轴运动了8 m
8.一列简谐横波沿x轴传播,t=0时刻的波形图如图所示。P、Q是波传播路径上的两个质点,t=0时刻,质点Q正向平衡位置运动,质点P的振动频率与摆长为0.25 m的单摆振动频率相同,取重力加速度g=π2 m/s2,则下列说法不正确的是 ( )
A.该波沿x轴正方向传播
B.该波的传播速度为0.4 m/s
C.质点Q在0~1.5 s内通过的路程为30 cm
D.质点P的振动方程为y=-5 sin 2πt cm
9.如图所示,一列沿x轴正方向传播的简谐横波,实线是t=0时刻的波形图,虚线是这列波经Δt=1.1 s的波形图,T<Δt<2T,则下列说法正确的是 ( )
A.这列波的波长是9 cm
B.这列波的周期是0.5 s
C.这列波的波速是10 m/s
D.从t=0时刻开始,x=5 cm处的质点经0.35 s振动到波峰
10.位于x=0.25 m的波源p从t=0时刻开始振动,形成的简谐横波沿x轴正负方向传播,在t=2.0 s时波源停止振动,t=2.1 s时的部分波形如图所示,其中质点a的平衡位置xa=1.75 m,质点b的平衡位置xb=-0.5 m。下列说法正确的是 ( )
A.沿x轴正负方向传播的波发生干涉
B.t=0.42 s时,波源的位移为负
C.t=2.25 s时,质点a沿y轴负方向振动
D.在0~2 s内,质点b运动的总路程是2.55 m
11.两列频率、振幅均相同的简谐波Ⅰ和Ⅱ分别从绳子的两端持续相向传播,在相遇区域发生了干涉,在相距0.48 m的A、B间用频闪相机连续拍摄,依次获得1、2、3、4、5五个波形,如图所示,且1和5是同一振动周期内绳上各点位移都达到最大值时拍摄的波形。已知频闪时间间隔为0.12 s,下列说法正确的是 ( )
A.简谐波Ⅰ和Ⅱ的波长均为0.24 m
B.简谐波Ⅰ和Ⅱ的周期均为0.48 s
C.绳上各点均做振幅相同的简谐运动
D.两波源到A点和C点的路程差之差的绝对值是0.48 m
12.多个点波源在空间也可以形成干涉图样,如图甲所示是利用软件模拟出某时刻三个完全相同的横波波源产生的干涉图样。图乙是三个完全相同的横波波源在均匀介质中的位置图示,波源S1、S2、S3分别位于等边三角形的三个顶点上,三角形的边长为2 m。三个波源t=0时刻同时开始振动,振动方向垂直纸面,振动图像均如图丙所示。已知波的传播速度为0.25 m/s,O处质点位于三角形中心,C处质点位于S2与S3连线中点。下列说法正确的是 ( )
A.位于O处的质点的振幅为2 cm
B.其中一列波遇到尺寸为0.8 m的障碍物时,不能发生明显的衍射现象
C.t=4.5 s时,C处质点与平衡位置之间的距离是2 cm
D.由于三列波在同一种介质中传播,所以三列波的频率不相等也能够发生干涉现象
二、非选择题(本题共5小题,共64分)
13.(8分)如图所示,甲为某一简谐横波在t=1.0 s时的图像,乙为该波传播方向上P质点的振动图像。
(1)求该波的波速大小v;
(2)求再经过3.5 s,P质点通过的路程s和位移y。
14.(10分)一根水平长绳一端P固定,某同学抓住长绳的另一端S在竖直方向上下振动。绳子上有A、B两点,水平时距离S分别为4 m和10 m。波沿绳子传播的速度v=4 m/s,当A点在平衡位置竖直向上振动时,B点恰好在平衡位置竖直向下振动,A、B之间仅有2个质点在平衡位置。求:
(1)A、B两点起振的时间差Δt;
(2)S点在竖直方向振动的频率f。
15.(14分)如图所示,一根张紧的水平弹性长绳上的a、b两点相距L=12.0 m,b点在a点的右方。一列简谐横波沿此长绳向右传播。在t=0时刻,a点的位移ya=4 cm(4 cm为质点振动的振幅),b点的位移yb=0,且向下运动,T=2 s。
(1)求质点a的振动方程;
(2)若这一列简谐波的波长λ
(1)求波的波长λ;
(2)求波的传播速度v;
(3)圆弧上还有几个振幅始终为零的点,其中e点(图中未画出)是与d点相邻的振幅为零的点,求线段be与ae的差。
17.(18分)水面上水波的传播速度跟水的深度有关,其关系式为v=,式中h为水的深度,g为重力加速度。如图甲所示是某水域的剖面图,C、D两部分深度不同,图乙是俯视示意图,O点处于两部分水面分界线上,M和N分别是处在C和D两区域水面上的点。t=0时刻O点从平衡位置向上振动,形成以O点为波源向左和向右传播的水波(可看作是简谐横波)。t=2.5 s时O点第二次到达波峰,此时M点第一次到达波峰。已知D区域水波振幅A=5 cm,水深hD=0.90 m,O、M间距离4.0 m,O、N间距离3.0 m。求:
(1)C区域的水深hC;
(2)N点在t=3 s时的振动方向及此时的位移;
(3)t=10 s时,处在D区域水面上的Q点(图中未标出)处于波峰,且O、Q间只有一个波峰,则Q点在t=0至t=10 s时间内振动的路程是多少
答案全解全析
1.D 根据题意,为使水波能带动树叶明显振动,即发生明显衍射现象,应减小障碍物的尺寸或者增大波长,根据λ=可知,减小波源的频率,波长增大,选项C错误,D正确;减小波源的振幅、减小波源距桥墩的距离对波长无影响,选项A、B错误。
2.B 振动方向与传播方向垂直,则“人浪”是横波,A错误;“人浪”只传播“下蹲、起立”这种运动形式,学生不会随波移动,B正确,C错误;“人浪”传播速度的快慢与人“下蹲、起立”的动作频繁程度无直接关系,D错误。
3.D 波向右传播,由带动法可知,此时刻质点P向下运动,A错误;此时,右侧刚开始运动的质点向下运动,则波源的起振方向向下,B错误;由图可知,波长逐渐增大,而波速由介质决定,波速不变,根据λ=vT,则周期逐渐增大,频率逐渐减小,C错误,D正确。
4.D 汽车降噪过程应用的是声波的叠加原理,抵消声波的振幅和频率应与环境噪声的振幅和频率相同,则抵消声波的振幅为A,频率应为f== Hz=50 Hz,故A、B、C错误;波速由介质决定,抵消声波和环境噪声在空气中传播的速度大小相等,D正确。
5.D t=0时波源开始振动,由波源振动方程可知,波源从平衡位置开始振动,起振方向沿y轴正方向,而波传播方向上各质点的起振方向与波源均相同,故t=T时,波向x轴正方向传播的距离为一个波长,且最右侧质点位于平衡位置,振动方向沿y轴正方向,根据“上下坡法”可知t=T时的波形图为D。
6.C a点是波谷与波谷相遇点,b点是波峰与波峰相遇点,c、d两点是波峰与波谷相遇点,则a、b两点是振动加强的,且a、b连线上的点也是振动加强的,c、d两点是振动减弱的;a、b两点连线中点未到达波峰或波谷,故速度不为0,选项A、B错误。a处于波谷,速度为零;b处于波峰,速度为零;c、d两点波峰与波谷相遇,速度为零,即四点的速度均为0,选项C正确;再经过周期c、d两点振动仍然减弱,选项D错误。
7.C 根据题图乙可知,平衡位置处于x=4 m处的质点M在t=0时沿着y轴正方向振动,则由“同侧法”可知,该列波沿x轴负方向传播,A错误;波的波长λ=4 m,周期T=2 s,则该列波的传播速度为v==2 m/s,B错误;由于7 s=3T,则质点M通过的路程为s=3×4A=14×20 cm=280 cm,C正确;质点只在平衡位置附近上下振动,并不会随波迁移,D错误。
8.D t=0时刻,质点Q正向平衡位置运动,根据“上下坡法”可以判断该波沿x轴正方向传播,A说法正确;摆长为0.25 m的单摆的振动频率f== =1 Hz,因此该波的周期T==1 s,由题图可知该波的波长为0.4 m,故波传播的速度为v==0.4 m/s,故B说法正确;由于波的周期为1 s,1.5 s=1.5T,所以质点Q在1.5 s内通过的路程为s=6A=30 cm,C说法正确;质点P振动的圆频率为ω==2π rad/s,t=0时刻质点P从平衡位置向y轴正方向振动,故振动方程为y=A sin ωt=5 sin 2πt cm,故D错误。
9.D 由波形图可知,这列波的波长λ=6 cm,A错误;由于波沿x轴正方向传播,且T<Δt<2T,故由图像可知,Δt=1.1 s内波传播的距离Δx=λ+λ=λ=11 cm,则Δt=T=1.1 s,故波的周期T=0.6 s,B错误;这列波的波速v===10 cm/s,C错误;t=0时刻x1=1.5 cm处的质点位于波峰,从t=0时刻开始,该波峰第一次传播到x=5 cm处,经历的时间t===0.35 s,D正确。
10.D 波从波源发出后,向x轴正、负方向传播即向相反方向传播,波不会相遇,故不会发生干涉,A错误。由题图可知,波的波长λ=1 m,0.1 s内波传播四分之一波长,可得=0.1 s,解得T=0.4 s;根据“同侧法”可知,波源的起振方向向上,根据周期性并结合波的图像可知,t=0.42 s即T
11.D 由图知,简谐波Ⅰ和Ⅱ的波长均为0.48 m,A错误;1和5是同一振动周期内绳上各点位移都达到最大值时拍摄的波形,相差半个周期,故简谐波Ⅰ和Ⅱ的周期均为0.96 s,B错误;图中除A、C、B三点为振动减弱点,振幅为零外,其他各点振幅不为零,故C错误;A、C是相邻的振动减弱点,两波源到A点和C点的路程差之差的绝对值等于波长0.48 m,D正确。
12.C O点位于正三角形的中心,该点到三个波源的距离相等,可知O处质点为振动加强点,则该点的振幅为3A=3×2 cm=6 cm,A错误。根据题图丙可知,该波的周期为4 s,根据波速公式v=,可得λ=1 m>0.8 m,根据发生明显衍射的条件可知,波遇到尺寸为0.8 m的障碍物时,能发生明显的衍射现象,B错误。根据几何关系可知S1C=S1S2 sin 60°= m,则波源S1的振动传播到C所需要时间t1==4 s>4.5 s,可知t=4.5 s时,波源S1的振动还没有传播到C点;波源S2与S3的振动传播到C所需要的时间均为t2= s=4 s<4.5 s,可知t=4.5 s时,波源S2与S3的振动传播到了C点,由于S2C=S3C=1 m=λ,4.5 s=T+,C处质点为振动加强点,表明C处质点4.5 s时刻的位移为波源S2与S3在时刻位移的叠加;图丙的振动方程为y=2 sin t (cm)=2 sin t (cm),当t=时,解得y0= cm,则t=4.5 s时,C处质点与平衡位置之间的距离是2y0=2 cm,C正确。根据发生干涉的条件可知,机械波要发生干涉,波的频率必须相等,即三列波的频率不相等不能够发生干涉现象,D错误。
13.答案 (1)4 m/s (2)2.8 m 0
解析 (1)由题图甲可得,该波的波长λ=4 m(1分)
由题图乙可得周期T=1 s(1分)
所以波速v==4 m/s(2分)
(2)由于3.5 s=7× (1分)
所以经过3.5 s质点通过的路程s=7×2A=2.8 m(1分)
由于波动具有重复性,经历时间为3.5个周期,P质点又回到图示位置,其位移为0 (2分)
14.答案 (1)1.5 s (2)1 Hz
解析 (1)波在介质中匀速传播,根据x=vt (2分)
可得A、B两点起振的时间差为Δt== s=1.5 s(2分)
(2)根据题意可画出A、B两点间的波形,如图所示 (2分)
可知xB-xA=1.5λ=6 m(1分)
解得λ=4 m(1分)
根据波速公式v=λf (1分)
解得振动的频率f=1 Hz(1分)
15.答案 (1)ya=4 sin cm(或ya=4 cos πt cm) (2) m/s(n=1,2,3,…)
解析 (1)设质点a的振动方程为ya=A sin (1分)
根据题意可得A=4 cm,T=2 s(1分)
可得ya=4 sin (πt+φ) cm(1分)
由t=0时刻,a点的位移ya=4 cm,可知4 cm=4 sin φ cm(1分)
解得φ= (1分)
则质点a的振动方程为ya=4 sin cm=4 cos πt cm(2分)
(2)当a、b两点间的距离小于波长时,波形如图所示 (1分)
根据题意有L=λ+nλ(n=0,1,2,3,…) (1分)
又已知λ
根据v=解得v= m/s(n=1,2,3,…) (2分)
16.答案 (1)(-1)R (2) (3)见解析
解析 (1)连接a、d,b、d,由几何关系可知∠dOa=60°,∠dba=30° (1分)
则ad=R (1分)
bd=R (1分)
d点是离c点最近的振幅极大的点,即振动加强点,有bd-ad=λ (2分)
所以波的波长λ=(-1)R (1分)
(2)由题图甲可知,波的周期T=2t0 (1分)
所以波的传播速度v== (2分)
(3)由题意可知,e点为振动减弱点,到两波源的距离之差等于半波长的奇数倍。 (1分)
若e点在圆弧上c、d之间,则有be-ae== (2分)
若e点在圆弧上a、d之间,则有be-ae== (2分)
17.答案 (1)0.40 m (2)向上振动 位移为0 (3)0.65 m
解析 (1)设波源O振动的周期为T,则有2.5 s=T (1分)
解得T=2 s(1分)
对M点的振动分析,知C区域水波波长为λC=OM=4 m(1分)
则有vC==2 m/s(1分)
根据v=求得hC=0.40 m(1分)
(2)由于D区域水深hD=0.90 m,由v= (1分)
可得D区域水波的传播速度vD==3 m/s(1分)
又由vD=解得波长λD=vDT=6 m(1分)
波传到N点所用的时间t1==1 s(1分)
所以t=3 s时,N点刚好完成一次全振动,可知其在平衡位置向上振动,位移为0。 (1分)
(3)t=10 s时,O点在平衡位置向上振动,可画出D区域水波的波动图像如图所示 (2分)
由图可知OQ=10.5 m(1分)
则有Δt== s=3.5 s(1分)
则Q点振动的时间为t2=10 s-3.5 s=6.5 s=3T (2分)
所以Q点振动的路程为s=3×4A=13A=0.65 m(2分)
