五年级暑假新课专项重点提升预习练:选择题(含解析)-2024-2025学年下学期小学数学人教版
文档属性
| 名称 | 五年级暑假新课专项重点提升预习练:选择题(含解析)-2024-2025学年下学期小学数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 310.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 10:42:46 | ||
图片预览




文档简介
五年级暑假新课专项重点提升预习练:选择题(含解析)-2024-2025学年下学期小学数学人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面说法不正确的是( )。
A.25+5=30是等式 B.5x+2>20是方程 C.方程一定是等式
2.两个因数相乘的积是3.5,其中一个因数扩大为原来的4倍,另一个因数也扩大为原来的4倍,那么积( )。
A.扩大为原来的4倍 B.扩大为原来的8倍
C.扩大为原来的16倍 D.不变
3.0.39×160=62.4,3.9×1.6的积是( )。
A.0.624 B.6.24 C.62.4 D.6240
4.有一幅长方形汴绣《清明上河图》,它是用36种颜色的真丝丝线绣成的,面积是1.2平方米,长是2米,那么这幅汴绣的宽是( )分米。
A.60 B.6 C.0.6
5.因为65×39=2535,所以下列各式错误的是( )。
A.6.5×39=253.5 B.0.65×3.9=0.2535
C.65×0.39=25.35 D.25.35÷0.039=650
6.13条短绳结成一根长绳,一共要打( )个结。
A.11 B.12 C.13 D.14
7.如图,两条平行线间的三个图形,( )的面积最大。
A.① B.② C.③
8.如图,笔算时,关于竖式箭头所指的“3”和“15”分别表示的是( )。
A.3个十分之一和15个一
B.3个十分之一和15个十分之一
C.3个一和15个十分之一
D.3个十分之一和15个百分之一
9.0.18313131…的循环节是( )。
A.831 B.31 C.13 D.313
10.在平面图上,点A和点B(6,4)在同一行,点A和点C(4,5)在同一列,那么点A的位置是( )。
A.(6,5) B.(5,4) C.(4,4) D.(4,6)
11.下列四个数中,最大的是( )。
A. B. C. D.0.074
12.下面的算式中,与5.8×10.1的结果不相等的是( )。
A.5.8×10+5.8 B.5.8×(10+0.1) C.5.8×10+5.8×0.1 D.2.9×20.2
13.如果点A用数对表示为(1,5),点B用数对表示为(1,1),点C用数对表示为(3,1),那么三角形ABC是( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
14.1.6÷0.3的商是5,余数是( )。
A.0.1 B.1 C.10
15.计算两个小数相乘的乘法题时,积是1.275,如果其中一个因数扩大到原来的10倍,另一个因数除以100,那么积是( )。
A.0.1275 B.12.75 C.127.5
16.( )的两个三角形一定可以拼成一个平行四边形。
A.面积相等 B.周长相等 C.完全一样 D.有一条边相等
17.7.5÷0.03与75×0.03的结果相比( )。
A.积大 B.商大 C.一样大 D.不确定
18.下面算式中,与9.66÷0.42的商相等的式子是( )。
A.96.6÷42 B.966÷42 C.0.966÷4.2
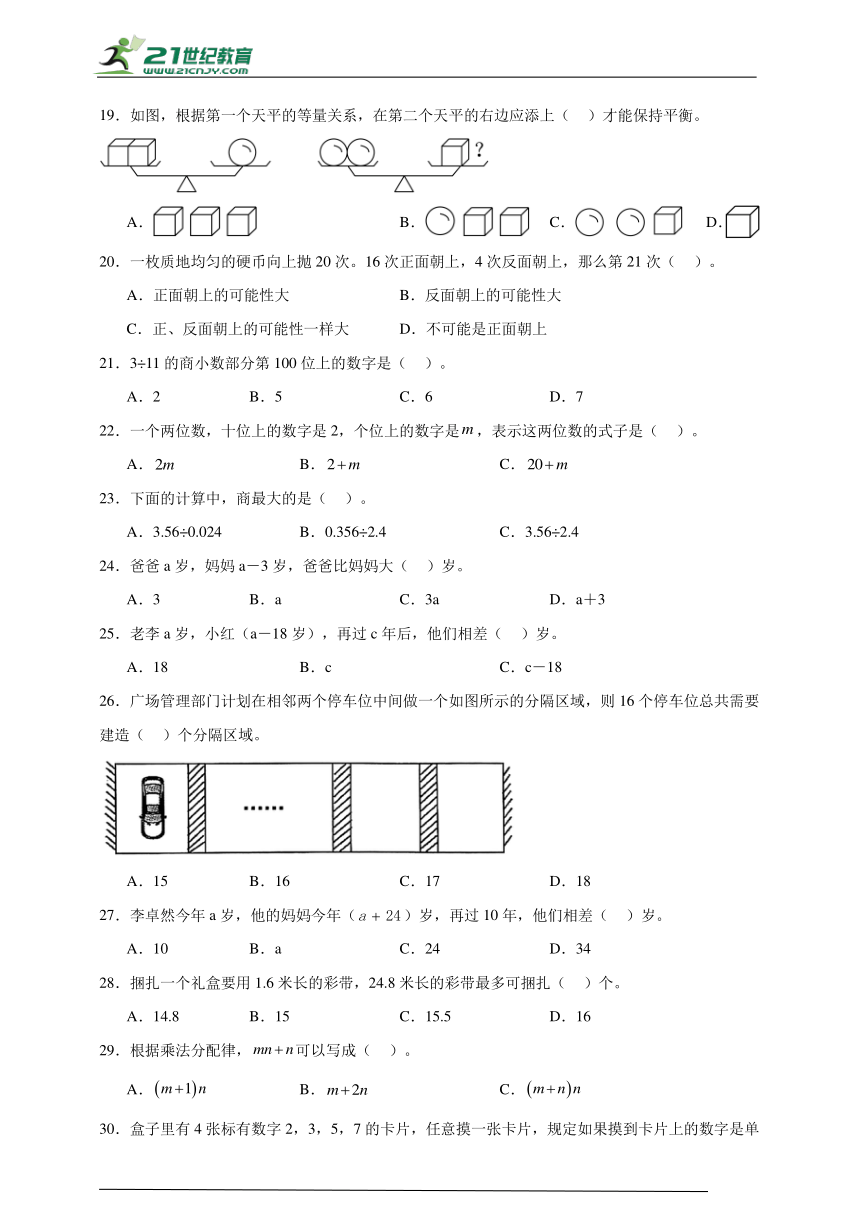
19.如图,根据第一个天平的等量关系,在第二个天平的右边应添上( )才能保持平衡。
A. B. C. D.
20.一枚质地均匀的硬币向上抛20次。16次正面朝上,4次反面朝上,那么第21次( )。
A.正面朝上的可能性大 B.反面朝上的可能性大
C.正、反面朝上的可能性一样大 D.不可能是正面朝上
21.3÷11的商小数部分第100位上的数字是( )。
A.2 B.5 C.6 D.7
22.一个两位数,十位上的数字是2,个位上的数字是,表示这两位数的式子是( )。
A. B. C.
23.下面的计算中,商最大的是( )。
A.3.56÷0.024 B.0.356÷2.4 C.3.56÷2.4
24.爸爸a岁,妈妈a-3岁,爸爸比妈妈大( )岁。
A.3 B.a C.3a D.a+3
25.老李a岁,小红(a-18岁),再过c年后,他们相差( )岁。
A.18 B.c C.c-18
26.广场管理部门计划在相邻两个停车位中间做一个如图所示的分隔区域,则16个停车位总共需要建造( )个分隔区域。
A.15 B.16 C.17 D.18
27.李卓然今年a岁,他的妈妈今年()岁,再过10年,他们相差( )岁。
A.10 B.a C.24 D.34
28.捆扎一个礼盒要用1.6米长的彩带,24.8米长的彩带最多可捆扎( )个。
A.14.8 B.15 C.15.5 D.16
29.根据乘法分配律,可以写成( )。
A. B. C.
30.盒子里有4张标有数字2,3,5,7的卡片,任意摸一张卡片,规定如果摸到卡片上的数字是单数小丽胜,摸到卡片上的数字是双数小华胜。谁胜的可能性大?( )
A.小丽 B.小华 C.一样 D.无法判断
31.是方程( )的解。
A. B. C. D.
32.计算28×0.25时,错误的方法是( )。
A.28×0.25=28×0.5×0.5 B.28×0.25=28×0.2+28×0.05
C.28×0.25=7×(4×0.25) D.28×0.25=20×0.2+8×0.25
33.下列式子中,与结果相同的是( )。
A. B.
C. D.
34.下面的四个式子中,哪一个是方程?( )
A.81÷9=9 B.n+16 C.4+a<56 D.3m+0.8=3.2
35.有30.8千克樱桃,已经装走了10篮,每篮2.1千克。剩下的樱桃用最多能装1.8千克的篮子装,一次装完,还需要( )个篮子。
A.18 B.5 C.6 D.17
36.1欧元兑换人民币9.15元,人民币2745元能兑换( )欧元。
A.2516.75 B.25116.75 C.2754.15 D.300
37.根据a×1.01=b×0.99(a、b均不为0),可以知道a与b的关系是( )。
A.a>b B.a<b C.a=b D.无法确定
38.1÷37的商,其小数点后面第60位上的数字是( )。
A.7 B.2 C.0 D.无法确定
39.小数部分第2022位是( )。
A.4 B.1 C.5 D.6
40.若0<a<1,那么5×a所得的积( )。
A.小于5 B.大于5 C.等于5 D.无法确定
41.下列算式中,与27.3÷1.5结果相同的是( )。
A.273÷15 B.2.73÷1.5 C.2.73÷15
42.下列问题中,不可以用算式43.4×0.8解决的是( )。
A.1千克樱桃43.4元,买0.8千克要花多少钱
B.一辆汽车的速度是43.4千米/时,0.8小时行多少千米
C.甲数是43.4,它是乙数的0.8倍,乙数是多少
D.一个长方形的长是43.4米,宽是0.8米,它的面积是多少
43.把一个平行四边形拉成一个长方形后( )。
A.面积不变 B.面积变小 C.面积变大
44.五子棋起源于中国,是全国智力运动会竞技项目之一。下图是两名同学的对弈情况,如果棋子A的位置记作(1,4),那么下一步黑棋子放在( )位置就获胜了。
A.(4,5) B.(6,4) C.(7,4) D.(4,7)
45.下列式子中,( )是方程。
A.12÷4+10 B.5.2-2×1.1=3
C.4.5x-5=4 D.x-2<5
46.美术课上,小强坐在第4列第3行,用数对(4,3)表示,明明坐在小强正后方第一个位置上,明明的位置用数对表示是( )。
A.(5,4) B.(4,4) C.(3,3) D.(5,3)
47.妈妈要把2.9千克香油分装在一些玻璃瓶里,每个瓶子最多可以装0.7千克香油,妈妈至少需要准备( )个这样的瓶子。
A.5 B.4.5 C.4
48.不计算9.□×1.54正确的积是( )。
A.14.63 B.1.463 C.146.3 D.0.1463
49.下面是方程的是( )。
A.7x-2>12 B.12+8=20 C.1.5a+2.3 D.39-3a=3
50.把一个长方形框拉成一个平行四边形,( )没变。
A.周长 B.面积 C.形状和大小 D.无法确定
《五年级暑假新课专项重点提升预习练:选择题(含解析)-2024-2025学年下学期小学数学人教版》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B B B B B B B C
题号 11 12 13 14 15 16 17 18 19 20
答案 B A C A A C B B A C
题号 21 22 23 24 25 26 27 28 29 30
答案 D C A A A A C B A A
题号 31 32 33 34 35 36 37 38 39 40
答案 D D C D C D B A A A
题号 41 42 43 44 45 46 47 48 49 50
答案 A C C B C B A A D A
1.B
【分析】方程是指含有未知数的等式;所以方程必须具备两个条件:①含有未知数;②等式;由此进行判断。
【详解】A.25+5=30是等式,说法正确;
B.5x+2>20不是等式,不是方程,说法错误;
C.含有未知数的等式是方程,所以方程一定是等式,说法正确。
故答案为:B
【点睛】此题考查方程的辨识:只有含有未知数的等式才是方程。
2.C
【分析】根据积的变化规律,一个因数不变,另一个因数扩大或缩小为原来的几倍(0除外),积也扩大或缩小为原来的相同的倍数;如果两个因数扩大为原来的相同的倍数(0除外),积扩大为原来的倍数就等于两个因数扩大为原来的倍数的乘积;由此解答。
【详解】根据积的变化规律可知,其中一个因数扩大为原来的4倍,另一个因数也扩大为原来的4倍,积扩大为原来的倍。
故答案选:C
【点睛】此题主要考查的是积的变化规律的灵活应用。
3.B
【分析】根据积的变化规律:如果一个因数扩大到原来的几倍,另一个因数不变,那么积也扩大到原来的几倍;如果一个因数缩小到原来的几分之一,另一个因数不变,那么积也缩小到原来的几分之一;据此解答。
【详解】一个因数0.39扩大到原来的10倍,变为3.9,另一个因数160缩小到原来的,变为1.6,积应缩小到原来的,即62.4÷10=6.24。
所以3.9×1.6=6.24。
故答案为:B
【点睛】此题的解题关键是灵活运用积的变化规律求解。
4.B
【分析】根据长方形面积公式,长方形的宽=面积÷长,列式计算即可,注意统一单位。
【详解】1.2÷2=0.6(米)=6(分米)
这幅汴绣的宽是6分米。
故答案为:B
5.B
【分析】小数乘法,小数乘法先按照整数乘法的计算方法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;如果小数的位数不够,需要在前面补0占位。
除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0补足);然后按除数是整数的小数除法进行计算;被除数的数用完时,在被除数的末尾添“0”继续除。
【详解】A.6.5×39=253.5,原题说法正确;
B.0.65×3.9=2.535,原题说法错误;
C.65×0.39=25.35,原题说法正确;
D.25.35÷0.039=650,原题说法正确。
故答案为:B
6.B
【分析】根据题意,两根绳子连接在一起要打一个结,把13根短绳结成一根长绳,打的结数要比绳子的根数少1,然后再根据题意进一步解答即可。
【详解】13-1=12(个)
一共要打12个结。
故答案为:B
【点睛】解答本题关键是明确:把几根绳子结成一根长绳,打的结数要比绳子的根数少1。
7.B
【分析】这三个图形中①是三角形,②是平行四边形,③是梯形,且这三个图形的高都是相等的,根据题目已知,结合三角形的面积=底×高÷2,平行四边形的面积=底×高,梯形的面积=(上底+下底)× 高÷2,代入相应数值计算,即可比较三个图形的面积大小。
【详解】假设这三个图形的高都是h,
则图形①面积:12×h÷2=6h;
图形②面积:7×h=7h;
图形③面积:(4+8)×h÷2
=12×h÷2
=6h
因为6=6<7,所以这三个图形中,图形②的面积最大。
故答案为:B
【点睛】解答本题的关键是抓住三个图形的高是相等的,结合三角形面积、平行四边形面积和梯形面积的计算公式即可得出结论。
8.B
【分析】计算除数是整数的小数除法,要按照整数除法的法则进行计算,商的小数点要和被除数的小数点对齐,除到小数部分有余数时,添0再除。每一步的余数都是与被除数的小数点对齐的数。
小数的计数单位是十分之一、百分之一、千分之一……,每相邻两个计数单位之间的进率是10。据此解答。
【详解】通过分析可得:“3”在商的十分位上,表示0.3;“15”与被除数的个位和十分位对齐,表示1.5。则竖式箭头所指的“3”和“15”分别表示的是3个十分之一和15个十分之一。
故答案为:B
9.B
【分析】一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。据此解答。
【详解】0.18313131…的循环节是31。
故答案为:B
10.C
【分析】用数对表示物体的位置的方法:数对的第一个数字表示列,第二个数字表示行。
点A和点B(6,4)在同一行,即点A在第4行;
点A和点C(4,5)在同一列,即点A在第4列;
据此用数对表示出点A的位置。
【详解】在平面图上,点A和点B(6,4)在同一行,点A和点C(4,5)在同一列,则点A在第4列第4行,那么点A的位置是(4,4)。
故答案为:C
【点睛】本题考查数对与位置的知识,明确在同一列,是数对的第一个数字相同;在同一行,是数对的第二个数字相同。
11.B
【分析】循环小数记数时,在第一个循环节的第一个数字和最末一个数字上分别记上一个圆点(循环节只有一个数字的只记一个圆点)“· ”,表示这个循环小数的这几个(或一个)数字重复出现。
比较小数的大小:(1)看它们的整数部分,整数部分大的那个数就大;(2)整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大,依次往右进行比较,直到比出大小为止。
【详解】>>>0.074,最大的是。
故答案为:B
12.A
【分析】计算5.8×10.1可采用简便方法,把10.1拆解(10+0.1)再通过乘法分配律进行简便计算;或者把5.8拆解成2.9×2,再通过乘法结合律进行计算,即可求出5.8×10.1的结果。
【详解】5.8×10.1
=5.8×(10+0.1)
=5.8×10+5.8×0.1
=58+0.58
=58.58
则B、C项与5.8×10.1的结果相等;
5.8×10.1
=(2.9×2)×10.1
=2.9×(2×10.1)
=2.9×20.2
=58.58
则D项与5.8×10.1的结果相等;
故答案为:A
13.C
【分析】根据各点的位置可以看出来,AB边与BC边相互垂直,所以三角形ABC是直角三角形。
【详解】如果点A用数对表示为(1,5),点B用数对表示为(1,1),点C用数对表示为(3,1),那么三角形ABC是直角三角形。
故答案为:C
【点睛】此题考查了学生对三角形的认识。要求学生熟练掌握并灵活运用。
14.A
【分析】根据有余数的除法中各部分的关系可知,余数=被除数-商×除数,据此解答。
【详解】1.6-5×0.3
=1.6-1.5
=0.1
所以,1.6÷0.3的商是5,余数是0.1。
故答案:A
【点睛】本题考查有余数的除法中各部分的关系的运用,也可以利用除数是小数的小数除法计算法则直接计算,求出余数。
15.A
【分析】根据积的变化规律,一个因数乘10,另一个因数除以100,则积除以100÷10=10,据此进行计算即可。
【详解】1.275÷(100÷10)
=1.275÷10
=0.1275
则积是0.1275。
故答案为:A
16.C
【分析】在拼组平行四边形时,平行四边形两组对边平行且相等,且有公共边,所以两个完全一样的,也就是形状和大小完全相同的三角形可以拼成一个平行四边形。
【详解】如图所示:
两个完全一样的三角形,一定可以拼成一个平行四边形;
故答案为:C
17.B
【分析】根据小数除法、乘法的计算法则,分别求出各算式的结果,然后进行比较,据此解答。
小数乘法,先按照整数乘法的计算方法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;如果小数的位数不够,需要在前面补0占位。
除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0补足);然后按除数是整数的小数除法进行计算。
【详解】7.5÷0.03=250
75×0.03=2.25
250>2.25
7.5÷0.03>75×0.03
所以,7.5÷0.03与75×0.03的结果相比商大。
故答案为:B
【点睛】本题考查小数乘法、除法的计算法则,并且能够正确熟练地进行计算。
18.B
【分析】商不变的规律是被除数和除数同时乘或除以相同的数0除外,商不变。逐项分析算式的商与题干里算式的商是否一致,据此解答。
【详解】A.9.66÷0.42=(9.66×10)÷(0.42×10)=96.6÷4.2,选项给出的算式不符合题意;
B.9.66÷0.42=(9.66×100)÷(0.42×100)=966÷42,选项给出的算式符合题意;
C.9.66÷0.42=(9.66÷10)÷(0.42÷10)=0.966÷0.042,选项给出的算式不符合题意。
故答案为:B
19.A
【分析】由图可知,2个正方体的质量=1个球的质量,根据等式的性质2,等式两边同时乘2,等式依然成立,即4个正方体的质量=2个球的质量,所以,需要在天平的右边添上3个正方体,据此解答即可。
【详解】由分析可知:
根据第一个天平的等量关系,在第二个天平的右边应添上3个正方体才能保持平衡。
故答案为:A
20.C
【分析】一枚硬币只有两个面,任意抛一次硬币,落地后正面朝上的可能性与反面朝上的可能性始终是相等的,所以无论前面几次的结果如何,第21次抛硬币,正面朝上的可能性与反面朝上的可能性相等。
【详解】一枚质地均匀的硬币向上抛20次。16次正面朝上,4次反面朝上,那么第21次正、反面朝上的可能性一样大。
故答案为:C
21.D
【分析】根据计算可知,3÷11的结果是循环小数,结果是一个循环小数,先找出循环节是几位数,要求商的小数部分第100为的数字是几,先求出100里面有多少组循环节,如果刚好整除,循环节的最后一个数就是要求的数;如果有余数,余数是几,就从循环节第1个数字向后数几个数字,据此解答。
【详解】3÷11=0.2727…
循环节是27;两个数字。
100÷2=50
商的小数部分第100为是7。
3÷11的商小数部分第100位上的数字是7。
故答案为:D
22.C
【分析】十位上的数字是几就表示有几个10,所以十位上的数字是2,表示2个十;个位上的数字是几就表示有几个1,个位上数字是m,表示m个一;把它们相加即可。
【详解】A.2m表示的是个位上数字的2倍,不符合题意;
B.2+m表示的是十位上的数字和个位上的数字相加之和,不符合题意;
C.20+m,表示这个两位数,符合题意。
故答案为:C
【点睛】解答本题的关键是掌握,两位数=十位数字×10+个位数字。
23.A
【分析】在除数算式中,当除数相同时,被除数越大商越大,据此比较B、C的大小;一个非0的数除以一个小于1的小数,结果大于这个数,除以一个大于1的小数,结果小于这个数,据此比较A、C的大小。
【详解】因为3.56>0.356,所以3.56÷2.4>0.356÷2.4;
因为0.024<1,所以3.56÷0.024>3.56,又因为2.4>1,所以3.56÷2.4<3.56,所以3.56÷0.024>3.56÷2.4;
所以3.56÷0.024>3.56÷2.4>0.356÷2.4,即商最大的是3.56÷0.024。
故答案为:A
24.A
【分析】已知爸爸的年龄、妈妈的年龄,根据“爸爸的年龄-妈妈的年龄=相差的年龄”求出爸爸比妈妈大的岁数。
【详解】a-(a-3)
=a-a+3
=0+3
=3(岁)
故答案为:A
【点睛】用含有字母的式子表示稍复杂的数量关系时,可以先把字母看成一个实际的数,找出题中的数量关系,再用含有字母的式子表示出来。
25.A
【分析】根据年龄差不变的特点,再过a年后,他们的年龄差与今年的年龄差相同,即用老李今年的年龄减去小红今年的年龄即可。
【详解】a-(a-18)
=a-a+18
=18(岁)
再过c年后,他们相差18岁。
故答案为:A
26.A
【分析】根据两端都栽的植树问题:“间隔数=棵数-1”,据此用停车位的个数减去1即可解答。
【详解】16-1=15(个)
所以16个停车位总共需要建造15个分隔区域。
故答案为:A
27.C
【分析】李卓然今年a岁,他的妈妈今年( a+24 )岁,李卓然与他妈妈相差24岁,再过10年,他们的年龄差不变,据此解答即可。
【详解】
所以李卓然与他妈妈相差24岁,再过10年,他们的年龄差不变,仍然是24岁。
故答案为:C
【点睛】本题考查用字母表示数,解答本题的关键是掌握年龄差的概念。
28.B
【分析】最后无论剩下多长彩带,只要不够捆扎一个礼盒,就无法捆扎一个礼盒,用彩带的长度÷捆扎一个礼盒需要的彩带的长度,结果用“去尾法”取整数。
【详解】24.8÷1.6≈15(个)
捆扎一个礼盒要用1.6米长的彩带,24.8米长的彩带最多可捆扎15个。
故答案为:B
29.A
【分析】乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。乘法分配律反过来同样适用,据此分析。
【详解】
根据乘法分配律,可以写成。
故答案为:A
30.A
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。先分别找出数字2,3,5,7里面的单数和双数,如果单数的个数多,则小丽赢的可能性大,如果双数的个数多,则小华的可能性大,如果单数和双数的个数相等,则两人赢的可能性一样大。
【详解】数字2,3,5,7里面,2是双数,共1个,3,5,7是单数,共3个;
1<3
小丽赢的可能性大。
故答案为:A
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
31.D
【分析】用等式的性质解方程,找出是哪个方程的解即可。
等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【详解】A.
解:
是方程的解,不符合题意;
B.
解:
是方程的解,不符合题意;
C.
解:
是方程的解,不符合题意;
D.
解:
是方程的解,符合题意。
故答案为:D
32.D
【分析】可以把0.25化成0.5×0.5,也可以把0.25化成0.2+0.05;也可以把28化为7×4,也可以把28化为20+8;再根据乘法分配律,乘法结合律,进行解答。
【详解】A.28×0.25
=28×(0.5×0.5)
=28×0.5×0.5
所以28×0.25=28×0.5×0.5正确;
B.28×0.25
=28×(0.2+0.05)
=28×0.2+28×0.05
所以28×0.25=28×0.2+28×0.05正确;
C.28×0.25
=7×4×0.25
=7×(4×0.25)
所以28×0.25=7×(4×0.25)正确;
D.28×0.25
=(20+8)×0.25
=20×0.25+8×0.25
所以28×0.25=20×0.2+8×0.25错误。
计算28×0.25时,错误的方法是28×0.25=20×0.2+8×0.25。
故答案为:D
33.C
【分析】8.08×125可以将8.08拆分成8+0.08或8×1.01,再利用乘法分配律进行计算即可。
【详解】8.08×125
=8×1.01×125
=1.01×(8×125)
=1.01×1000
=1010
故答案为:C
【点睛】此题考查乘法分配律在小数乘法计算中的应用。
34.D
【分析】方程是指含有未知数的等式,所以方程必须具备两个条件:(1)含有未知数;(2)等式;由此进行解答。
【详解】A.81÷9=9,不含未知数,是等式,不是方程;
B.n+16,含有未知数,不是等式,不是方程;
C.4+a<56,含有未知数,不是等式,不是方程;
D.3m+0.8=3.2,含有未知数,是等式,是方程。
故答案为:D
35.C
【分析】根据乘法的意义,用2.1乘10求出已经装走的樱桃重量,再用30.8减去已经装走的重量,即可求出剩下的樱桃重量。求剩下的需要几个篮子来装,就是求剩下的重量里面有几个1.8千克,根据除法的意义,用剩下的重量除以1.8即可解答。结果需要用“进一法”取整数值。
【详解】(30.8-2.1×10)÷1.8
=(30.8-21)÷1.8
=9.8÷1.8
≈6(个)
则还需要6个篮子。
故答案为:C
36.D
【分析】把人民币2745元化成欧元数,用2745除以汇率9.15,即可得解。
【详解】2745÷9.45=300(欧元)
人民币2745元能兑换300欧元。
故答案为:D
【点睛】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
37.B
【分析】两个非0的因数相乘的积相等,一个因数越大,另一个因数越小,据此解答即可。
【详解】a×1.01=b×0.99,且a、b均不为0,
因为1.01>0.99,所以a<b,
故答案为:B
【点睛】明确两个非0的因数相乘的积相等,一个因数越大,另一个因数越小是解题的关键。
38.A
【分析】根据小数除法的计算方法进行计算,商用循环小数表示,找到循环节,即周期,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数格周期多n个,也就是余数是n,那么结果为下一个周期里的第n个。
【详解】1÷37=
60÷3=20(组)
1÷37的商,其小数点后面第60位上的数字是7。
故答案为:A
【点睛】关键是掌握循环小数的记数方法,会解决简单的周期问题。
39.A
【分析】从小数点后面第2位开始,每5位数字一循环,计算第2022位数字是第几组循环零几个数字,即可判断是多少。
【详解】(2022-1)÷5
=2021÷5
=404(组)……1(位)
余数是1,所以小数部分第2022位上的数字是4。
故答案为:A
【点睛】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
40.A
【分析】一个数(0除外)乘小于1的数,积比原来的数小。
【详解】如:a=0.1,5×a=5×0.1=0.5,0.5<5。
所以,若0<a<1,那么5×a所得的积小于5。
故答案为:A
【点睛】掌握不用计算判断积与因数之间大小关系的方法是解题的关键。
41.A
【分析】利用商不变的规律,看哪个除法算式的被除数和除数同时乘或除以相同的数(0除外)后,能变成27.3÷1.5,那么这两个算式的结果相同。
商不变的规律:被除数和除数同时乘(或除以)一个相同的数(0除外),商不变。
【详解】A.273÷15=(273÷10)÷(15÷10)=27.3÷1.5
所以,273÷15与27.3÷1.5结果相同;
B.2.73÷1.5=(2.73×10)÷(1.5×10)=27.3÷15
27.3÷15≠27.3÷1.5,所以2.73÷1.5与27.3÷1.5结果不相同;
C.2.73÷15=(2.73×10)÷(15×10)=27.3÷150
27.3÷150≠27.3÷1.5,所以2.73÷15与27.3÷1.5结果不相同。
故答案为:A
42.C
【分析】根据单价×数量=总价,路程=速度×时间,倍数的含义,长方形的面积=长×宽,即可解答。
【详解】A.1千克樱桃43.4元,买0.8千克要花多少钱,列式:43.4×0.8,符合题意;
B.一辆汽车的速度是43.4千米/时,0.8小时行多少千米,列式:43.4×0.8,符合题意;
C.甲数是43.4,它是乙数的0.8倍,乙数是多少,列式:43.4÷0.8,不符合题意;
D.一个长方形的长是43.4米,宽是0.8米,它的面积是多少,列式:43.4×0.8,符合题意。
故答案为:C
【点睛】本题考查了利用小数乘除法解决问题,需准确分析各选项中的数量关系,准确解答。
43.C
【分析】把平行四边形拉成长方形后,四条边的长度没变,所以周长不变,但对应底上的高变长了,平行四边形和长方形的面积都等于底乘高,当底不变,高变大,则面积变大了;据此解答。
【详解】如图:
把一个平行四边形拉成一个长方形后,周长不变,底边长不变,它的高变大了,所以面积变大。
故答案为:C
【点睛】此题主要考查平行四边形的特征以及平行四边形、长方形面积公式的综合应用。
44.B
【分析】明确数对的概念:数对是一个表示位置的概念,相当于坐标,前一个数字表示列,后一个数字表示行。分析棋子的位置:已知棋子A的位置记作(1,4),说明第1列第4行。确定黑棋子获胜的位置:观察棋盘,黑棋子在第4行已经有4个棋子,再在第6列第4行放一个棋子,就能形成5个连续的棋子,从而获胜。
【详解】棋子A在(1,4),表示第1列第4行。黑棋子在第4行已有4个,在(6,4)位置放棋子可形成5连。
故答案为:B
45.C
【分析】含有未知数的等式叫做方程,可据此逐项分析,再做选择即可。
【详解】A.12÷4+10,这可以看作一个算式,但没有算出结果,不是方程;
B.5.2-2×1.1=3,这是一个等式,不含有未知数,不是方程;
C.4.5x-5=4,这是一个含有未知数的等式,是方程;
D.x-2<5,这个式子含有未知数,但不是等式,不是方程。
这些式子中,4.5x-5=4是方程。
故答案为:C
【点睛】需要明确方程的含义,一方面需要含有字母,即未知数;同时还得是等式;二者缺一不可。
46.B
【分析】根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行;明明坐在小强正后方第一个位置上,则明明与小强在同一列,用小强的行数加1即是明明的行数。
【详解】3+1=4
则明明坐在小强正后方第一个位置上,明明的位置用数对表示是(4,4)。
故答案为:B
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
47.A
【分析】用香油的总质量除以一个瓶子最多可以装的质量,利用“进一法”即可求出至少需要准备几个这样的瓶子。
【详解】2.9÷0.7≈4.1≈5(个)
则妈妈至少需要准备5个这样的瓶子。
故答案为:A
48.A
【分析】一个数(0除外)乘大于1的数,积比原来的数大。
因为1.54>1,所以9.□×1.54>9.□;因为9.□×2≥18,所以9.□<9.□×1.54<18;比较四个选项中的积,在9.□~18范围内的,就是9.□×1.54正确的积。
【详解】1<1.54<2,所以9.□<9.□×1.54<18;
A.9.□<14.63<18,符合题意;
B.1.463<9.□,不符合题意;
C.146.3>18,不符合题意;
D.0.1463<9.□,不符合题意;
不计算9.□×1.54正确的积是14.63。
故答案为:A
【点睛】掌握判断积与因数之间大小关系的方法是解题的关键。
49.D
【分析】根据方程的意义:含有未知数的等式叫做方程,方程具备两个条件:一含有未知数,二必须是等式,据此解答。
【详解】A.7x-2>12,含有未知数,不是等式,不是方程;
B.12+8=20,是等式,不含有未知数,不是方程;
C.1.5a+2.3,含有未知数,不是等式,不是方程;
D.39-3a=3,含有未知数,是等式,是方程。
故答案为:D
50.A
【分析】把长方形拉成平行四边形,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形底边的邻边,则长方形周长等于平行四边形的周长,比较长方形的宽和平行四边形高的大小关系,即可求得长方形的面积和平行四边形面积的大小关系,据此解答。
【详解】
长方形的周长=(长+宽)×2
平行四边形的周长=(底边+邻边)×2
由图可知,长方形的长等于平行四边形的底,宽等于平行四边形底边的邻边,因此周长不变。
长方形的面积=长×宽
平行四边形的面积=底×高
由图可知,把长方形拉成平行四边形,随着拉动,高逐渐变小,但底不变。
因此面积变小了。
故答案为:A
【点睛】分析长方形的宽和平行四边形的高的大小关系是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面说法不正确的是( )。
A.25+5=30是等式 B.5x+2>20是方程 C.方程一定是等式
2.两个因数相乘的积是3.5,其中一个因数扩大为原来的4倍,另一个因数也扩大为原来的4倍,那么积( )。
A.扩大为原来的4倍 B.扩大为原来的8倍
C.扩大为原来的16倍 D.不变
3.0.39×160=62.4,3.9×1.6的积是( )。
A.0.624 B.6.24 C.62.4 D.6240
4.有一幅长方形汴绣《清明上河图》,它是用36种颜色的真丝丝线绣成的,面积是1.2平方米,长是2米,那么这幅汴绣的宽是( )分米。
A.60 B.6 C.0.6
5.因为65×39=2535,所以下列各式错误的是( )。
A.6.5×39=253.5 B.0.65×3.9=0.2535
C.65×0.39=25.35 D.25.35÷0.039=650
6.13条短绳结成一根长绳,一共要打( )个结。
A.11 B.12 C.13 D.14
7.如图,两条平行线间的三个图形,( )的面积最大。
A.① B.② C.③
8.如图,笔算时,关于竖式箭头所指的“3”和“15”分别表示的是( )。
A.3个十分之一和15个一
B.3个十分之一和15个十分之一
C.3个一和15个十分之一
D.3个十分之一和15个百分之一
9.0.18313131…的循环节是( )。
A.831 B.31 C.13 D.313
10.在平面图上,点A和点B(6,4)在同一行,点A和点C(4,5)在同一列,那么点A的位置是( )。
A.(6,5) B.(5,4) C.(4,4) D.(4,6)
11.下列四个数中,最大的是( )。
A. B. C. D.0.074
12.下面的算式中,与5.8×10.1的结果不相等的是( )。
A.5.8×10+5.8 B.5.8×(10+0.1) C.5.8×10+5.8×0.1 D.2.9×20.2
13.如果点A用数对表示为(1,5),点B用数对表示为(1,1),点C用数对表示为(3,1),那么三角形ABC是( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
14.1.6÷0.3的商是5,余数是( )。
A.0.1 B.1 C.10
15.计算两个小数相乘的乘法题时,积是1.275,如果其中一个因数扩大到原来的10倍,另一个因数除以100,那么积是( )。
A.0.1275 B.12.75 C.127.5
16.( )的两个三角形一定可以拼成一个平行四边形。
A.面积相等 B.周长相等 C.完全一样 D.有一条边相等
17.7.5÷0.03与75×0.03的结果相比( )。
A.积大 B.商大 C.一样大 D.不确定
18.下面算式中,与9.66÷0.42的商相等的式子是( )。
A.96.6÷42 B.966÷42 C.0.966÷4.2
19.如图,根据第一个天平的等量关系,在第二个天平的右边应添上( )才能保持平衡。
A. B. C. D.
20.一枚质地均匀的硬币向上抛20次。16次正面朝上,4次反面朝上,那么第21次( )。
A.正面朝上的可能性大 B.反面朝上的可能性大
C.正、反面朝上的可能性一样大 D.不可能是正面朝上
21.3÷11的商小数部分第100位上的数字是( )。
A.2 B.5 C.6 D.7
22.一个两位数,十位上的数字是2,个位上的数字是,表示这两位数的式子是( )。
A. B. C.
23.下面的计算中,商最大的是( )。
A.3.56÷0.024 B.0.356÷2.4 C.3.56÷2.4
24.爸爸a岁,妈妈a-3岁,爸爸比妈妈大( )岁。
A.3 B.a C.3a D.a+3
25.老李a岁,小红(a-18岁),再过c年后,他们相差( )岁。
A.18 B.c C.c-18
26.广场管理部门计划在相邻两个停车位中间做一个如图所示的分隔区域,则16个停车位总共需要建造( )个分隔区域。
A.15 B.16 C.17 D.18
27.李卓然今年a岁,他的妈妈今年()岁,再过10年,他们相差( )岁。
A.10 B.a C.24 D.34
28.捆扎一个礼盒要用1.6米长的彩带,24.8米长的彩带最多可捆扎( )个。
A.14.8 B.15 C.15.5 D.16
29.根据乘法分配律,可以写成( )。
A. B. C.
30.盒子里有4张标有数字2,3,5,7的卡片,任意摸一张卡片,规定如果摸到卡片上的数字是单数小丽胜,摸到卡片上的数字是双数小华胜。谁胜的可能性大?( )
A.小丽 B.小华 C.一样 D.无法判断
31.是方程( )的解。
A. B. C. D.
32.计算28×0.25时,错误的方法是( )。
A.28×0.25=28×0.5×0.5 B.28×0.25=28×0.2+28×0.05
C.28×0.25=7×(4×0.25) D.28×0.25=20×0.2+8×0.25
33.下列式子中,与结果相同的是( )。
A. B.
C. D.
34.下面的四个式子中,哪一个是方程?( )
A.81÷9=9 B.n+16 C.4+a<56 D.3m+0.8=3.2
35.有30.8千克樱桃,已经装走了10篮,每篮2.1千克。剩下的樱桃用最多能装1.8千克的篮子装,一次装完,还需要( )个篮子。
A.18 B.5 C.6 D.17
36.1欧元兑换人民币9.15元,人民币2745元能兑换( )欧元。
A.2516.75 B.25116.75 C.2754.15 D.300
37.根据a×1.01=b×0.99(a、b均不为0),可以知道a与b的关系是( )。
A.a>b B.a<b C.a=b D.无法确定
38.1÷37的商,其小数点后面第60位上的数字是( )。
A.7 B.2 C.0 D.无法确定
39.小数部分第2022位是( )。
A.4 B.1 C.5 D.6
40.若0<a<1,那么5×a所得的积( )。
A.小于5 B.大于5 C.等于5 D.无法确定
41.下列算式中,与27.3÷1.5结果相同的是( )。
A.273÷15 B.2.73÷1.5 C.2.73÷15
42.下列问题中,不可以用算式43.4×0.8解决的是( )。
A.1千克樱桃43.4元,买0.8千克要花多少钱
B.一辆汽车的速度是43.4千米/时,0.8小时行多少千米
C.甲数是43.4,它是乙数的0.8倍,乙数是多少
D.一个长方形的长是43.4米,宽是0.8米,它的面积是多少
43.把一个平行四边形拉成一个长方形后( )。
A.面积不变 B.面积变小 C.面积变大
44.五子棋起源于中国,是全国智力运动会竞技项目之一。下图是两名同学的对弈情况,如果棋子A的位置记作(1,4),那么下一步黑棋子放在( )位置就获胜了。
A.(4,5) B.(6,4) C.(7,4) D.(4,7)
45.下列式子中,( )是方程。
A.12÷4+10 B.5.2-2×1.1=3
C.4.5x-5=4 D.x-2<5
46.美术课上,小强坐在第4列第3行,用数对(4,3)表示,明明坐在小强正后方第一个位置上,明明的位置用数对表示是( )。
A.(5,4) B.(4,4) C.(3,3) D.(5,3)
47.妈妈要把2.9千克香油分装在一些玻璃瓶里,每个瓶子最多可以装0.7千克香油,妈妈至少需要准备( )个这样的瓶子。
A.5 B.4.5 C.4
48.不计算9.□×1.54正确的积是( )。
A.14.63 B.1.463 C.146.3 D.0.1463
49.下面是方程的是( )。
A.7x-2>12 B.12+8=20 C.1.5a+2.3 D.39-3a=3
50.把一个长方形框拉成一个平行四边形,( )没变。
A.周长 B.面积 C.形状和大小 D.无法确定
《五年级暑假新课专项重点提升预习练:选择题(含解析)-2024-2025学年下学期小学数学人教版》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B B B B B B B C
题号 11 12 13 14 15 16 17 18 19 20
答案 B A C A A C B B A C
题号 21 22 23 24 25 26 27 28 29 30
答案 D C A A A A C B A A
题号 31 32 33 34 35 36 37 38 39 40
答案 D D C D C D B A A A
题号 41 42 43 44 45 46 47 48 49 50
答案 A C C B C B A A D A
1.B
【分析】方程是指含有未知数的等式;所以方程必须具备两个条件:①含有未知数;②等式;由此进行判断。
【详解】A.25+5=30是等式,说法正确;
B.5x+2>20不是等式,不是方程,说法错误;
C.含有未知数的等式是方程,所以方程一定是等式,说法正确。
故答案为:B
【点睛】此题考查方程的辨识:只有含有未知数的等式才是方程。
2.C
【分析】根据积的变化规律,一个因数不变,另一个因数扩大或缩小为原来的几倍(0除外),积也扩大或缩小为原来的相同的倍数;如果两个因数扩大为原来的相同的倍数(0除外),积扩大为原来的倍数就等于两个因数扩大为原来的倍数的乘积;由此解答。
【详解】根据积的变化规律可知,其中一个因数扩大为原来的4倍,另一个因数也扩大为原来的4倍,积扩大为原来的倍。
故答案选:C
【点睛】此题主要考查的是积的变化规律的灵活应用。
3.B
【分析】根据积的变化规律:如果一个因数扩大到原来的几倍,另一个因数不变,那么积也扩大到原来的几倍;如果一个因数缩小到原来的几分之一,另一个因数不变,那么积也缩小到原来的几分之一;据此解答。
【详解】一个因数0.39扩大到原来的10倍,变为3.9,另一个因数160缩小到原来的,变为1.6,积应缩小到原来的,即62.4÷10=6.24。
所以3.9×1.6=6.24。
故答案为:B
【点睛】此题的解题关键是灵活运用积的变化规律求解。
4.B
【分析】根据长方形面积公式,长方形的宽=面积÷长,列式计算即可,注意统一单位。
【详解】1.2÷2=0.6(米)=6(分米)
这幅汴绣的宽是6分米。
故答案为:B
5.B
【分析】小数乘法,小数乘法先按照整数乘法的计算方法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;如果小数的位数不够,需要在前面补0占位。
除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0补足);然后按除数是整数的小数除法进行计算;被除数的数用完时,在被除数的末尾添“0”继续除。
【详解】A.6.5×39=253.5,原题说法正确;
B.0.65×3.9=2.535,原题说法错误;
C.65×0.39=25.35,原题说法正确;
D.25.35÷0.039=650,原题说法正确。
故答案为:B
6.B
【分析】根据题意,两根绳子连接在一起要打一个结,把13根短绳结成一根长绳,打的结数要比绳子的根数少1,然后再根据题意进一步解答即可。
【详解】13-1=12(个)
一共要打12个结。
故答案为:B
【点睛】解答本题关键是明确:把几根绳子结成一根长绳,打的结数要比绳子的根数少1。
7.B
【分析】这三个图形中①是三角形,②是平行四边形,③是梯形,且这三个图形的高都是相等的,根据题目已知,结合三角形的面积=底×高÷2,平行四边形的面积=底×高,梯形的面积=(上底+下底)× 高÷2,代入相应数值计算,即可比较三个图形的面积大小。
【详解】假设这三个图形的高都是h,
则图形①面积:12×h÷2=6h;
图形②面积:7×h=7h;
图形③面积:(4+8)×h÷2
=12×h÷2
=6h
因为6=6<7,所以这三个图形中,图形②的面积最大。
故答案为:B
【点睛】解答本题的关键是抓住三个图形的高是相等的,结合三角形面积、平行四边形面积和梯形面积的计算公式即可得出结论。
8.B
【分析】计算除数是整数的小数除法,要按照整数除法的法则进行计算,商的小数点要和被除数的小数点对齐,除到小数部分有余数时,添0再除。每一步的余数都是与被除数的小数点对齐的数。
小数的计数单位是十分之一、百分之一、千分之一……,每相邻两个计数单位之间的进率是10。据此解答。
【详解】通过分析可得:“3”在商的十分位上,表示0.3;“15”与被除数的个位和十分位对齐,表示1.5。则竖式箭头所指的“3”和“15”分别表示的是3个十分之一和15个十分之一。
故答案为:B
9.B
【分析】一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。据此解答。
【详解】0.18313131…的循环节是31。
故答案为:B
10.C
【分析】用数对表示物体的位置的方法:数对的第一个数字表示列,第二个数字表示行。
点A和点B(6,4)在同一行,即点A在第4行;
点A和点C(4,5)在同一列,即点A在第4列;
据此用数对表示出点A的位置。
【详解】在平面图上,点A和点B(6,4)在同一行,点A和点C(4,5)在同一列,则点A在第4列第4行,那么点A的位置是(4,4)。
故答案为:C
【点睛】本题考查数对与位置的知识,明确在同一列,是数对的第一个数字相同;在同一行,是数对的第二个数字相同。
11.B
【分析】循环小数记数时,在第一个循环节的第一个数字和最末一个数字上分别记上一个圆点(循环节只有一个数字的只记一个圆点)“· ”,表示这个循环小数的这几个(或一个)数字重复出现。
比较小数的大小:(1)看它们的整数部分,整数部分大的那个数就大;(2)整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大,依次往右进行比较,直到比出大小为止。
【详解】>>>0.074,最大的是。
故答案为:B
12.A
【分析】计算5.8×10.1可采用简便方法,把10.1拆解(10+0.1)再通过乘法分配律进行简便计算;或者把5.8拆解成2.9×2,再通过乘法结合律进行计算,即可求出5.8×10.1的结果。
【详解】5.8×10.1
=5.8×(10+0.1)
=5.8×10+5.8×0.1
=58+0.58
=58.58
则B、C项与5.8×10.1的结果相等;
5.8×10.1
=(2.9×2)×10.1
=2.9×(2×10.1)
=2.9×20.2
=58.58
则D项与5.8×10.1的结果相等;
故答案为:A
13.C
【分析】根据各点的位置可以看出来,AB边与BC边相互垂直,所以三角形ABC是直角三角形。
【详解】如果点A用数对表示为(1,5),点B用数对表示为(1,1),点C用数对表示为(3,1),那么三角形ABC是直角三角形。
故答案为:C
【点睛】此题考查了学生对三角形的认识。要求学生熟练掌握并灵活运用。
14.A
【分析】根据有余数的除法中各部分的关系可知,余数=被除数-商×除数,据此解答。
【详解】1.6-5×0.3
=1.6-1.5
=0.1
所以,1.6÷0.3的商是5,余数是0.1。
故答案:A
【点睛】本题考查有余数的除法中各部分的关系的运用,也可以利用除数是小数的小数除法计算法则直接计算,求出余数。
15.A
【分析】根据积的变化规律,一个因数乘10,另一个因数除以100,则积除以100÷10=10,据此进行计算即可。
【详解】1.275÷(100÷10)
=1.275÷10
=0.1275
则积是0.1275。
故答案为:A
16.C
【分析】在拼组平行四边形时,平行四边形两组对边平行且相等,且有公共边,所以两个完全一样的,也就是形状和大小完全相同的三角形可以拼成一个平行四边形。
【详解】如图所示:
两个完全一样的三角形,一定可以拼成一个平行四边形;
故答案为:C
17.B
【分析】根据小数除法、乘法的计算法则,分别求出各算式的结果,然后进行比较,据此解答。
小数乘法,先按照整数乘法的计算方法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;如果小数的位数不够,需要在前面补0占位。
除数是小数的小数除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0补足);然后按除数是整数的小数除法进行计算。
【详解】7.5÷0.03=250
75×0.03=2.25
250>2.25
7.5÷0.03>75×0.03
所以,7.5÷0.03与75×0.03的结果相比商大。
故答案为:B
【点睛】本题考查小数乘法、除法的计算法则,并且能够正确熟练地进行计算。
18.B
【分析】商不变的规律是被除数和除数同时乘或除以相同的数0除外,商不变。逐项分析算式的商与题干里算式的商是否一致,据此解答。
【详解】A.9.66÷0.42=(9.66×10)÷(0.42×10)=96.6÷4.2,选项给出的算式不符合题意;
B.9.66÷0.42=(9.66×100)÷(0.42×100)=966÷42,选项给出的算式符合题意;
C.9.66÷0.42=(9.66÷10)÷(0.42÷10)=0.966÷0.042,选项给出的算式不符合题意。
故答案为:B
19.A
【分析】由图可知,2个正方体的质量=1个球的质量,根据等式的性质2,等式两边同时乘2,等式依然成立,即4个正方体的质量=2个球的质量,所以,需要在天平的右边添上3个正方体,据此解答即可。
【详解】由分析可知:
根据第一个天平的等量关系,在第二个天平的右边应添上3个正方体才能保持平衡。
故答案为:A
20.C
【分析】一枚硬币只有两个面,任意抛一次硬币,落地后正面朝上的可能性与反面朝上的可能性始终是相等的,所以无论前面几次的结果如何,第21次抛硬币,正面朝上的可能性与反面朝上的可能性相等。
【详解】一枚质地均匀的硬币向上抛20次。16次正面朝上,4次反面朝上,那么第21次正、反面朝上的可能性一样大。
故答案为:C
21.D
【分析】根据计算可知,3÷11的结果是循环小数,结果是一个循环小数,先找出循环节是几位数,要求商的小数部分第100为的数字是几,先求出100里面有多少组循环节,如果刚好整除,循环节的最后一个数就是要求的数;如果有余数,余数是几,就从循环节第1个数字向后数几个数字,据此解答。
【详解】3÷11=0.2727…
循环节是27;两个数字。
100÷2=50
商的小数部分第100为是7。
3÷11的商小数部分第100位上的数字是7。
故答案为:D
22.C
【分析】十位上的数字是几就表示有几个10,所以十位上的数字是2,表示2个十;个位上的数字是几就表示有几个1,个位上数字是m,表示m个一;把它们相加即可。
【详解】A.2m表示的是个位上数字的2倍,不符合题意;
B.2+m表示的是十位上的数字和个位上的数字相加之和,不符合题意;
C.20+m,表示这个两位数,符合题意。
故答案为:C
【点睛】解答本题的关键是掌握,两位数=十位数字×10+个位数字。
23.A
【分析】在除数算式中,当除数相同时,被除数越大商越大,据此比较B、C的大小;一个非0的数除以一个小于1的小数,结果大于这个数,除以一个大于1的小数,结果小于这个数,据此比较A、C的大小。
【详解】因为3.56>0.356,所以3.56÷2.4>0.356÷2.4;
因为0.024<1,所以3.56÷0.024>3.56,又因为2.4>1,所以3.56÷2.4<3.56,所以3.56÷0.024>3.56÷2.4;
所以3.56÷0.024>3.56÷2.4>0.356÷2.4,即商最大的是3.56÷0.024。
故答案为:A
24.A
【分析】已知爸爸的年龄、妈妈的年龄,根据“爸爸的年龄-妈妈的年龄=相差的年龄”求出爸爸比妈妈大的岁数。
【详解】a-(a-3)
=a-a+3
=0+3
=3(岁)
故答案为:A
【点睛】用含有字母的式子表示稍复杂的数量关系时,可以先把字母看成一个实际的数,找出题中的数量关系,再用含有字母的式子表示出来。
25.A
【分析】根据年龄差不变的特点,再过a年后,他们的年龄差与今年的年龄差相同,即用老李今年的年龄减去小红今年的年龄即可。
【详解】a-(a-18)
=a-a+18
=18(岁)
再过c年后,他们相差18岁。
故答案为:A
26.A
【分析】根据两端都栽的植树问题:“间隔数=棵数-1”,据此用停车位的个数减去1即可解答。
【详解】16-1=15(个)
所以16个停车位总共需要建造15个分隔区域。
故答案为:A
27.C
【分析】李卓然今年a岁,他的妈妈今年( a+24 )岁,李卓然与他妈妈相差24岁,再过10年,他们的年龄差不变,据此解答即可。
【详解】
所以李卓然与他妈妈相差24岁,再过10年,他们的年龄差不变,仍然是24岁。
故答案为:C
【点睛】本题考查用字母表示数,解答本题的关键是掌握年龄差的概念。
28.B
【分析】最后无论剩下多长彩带,只要不够捆扎一个礼盒,就无法捆扎一个礼盒,用彩带的长度÷捆扎一个礼盒需要的彩带的长度,结果用“去尾法”取整数。
【详解】24.8÷1.6≈15(个)
捆扎一个礼盒要用1.6米长的彩带,24.8米长的彩带最多可捆扎15个。
故答案为:B
29.A
【分析】乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。乘法分配律反过来同样适用,据此分析。
【详解】
根据乘法分配律,可以写成。
故答案为:A
30.A
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。先分别找出数字2,3,5,7里面的单数和双数,如果单数的个数多,则小丽赢的可能性大,如果双数的个数多,则小华的可能性大,如果单数和双数的个数相等,则两人赢的可能性一样大。
【详解】数字2,3,5,7里面,2是双数,共1个,3,5,7是单数,共3个;
1<3
小丽赢的可能性大。
故答案为:A
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
31.D
【分析】用等式的性质解方程,找出是哪个方程的解即可。
等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【详解】A.
解:
是方程的解,不符合题意;
B.
解:
是方程的解,不符合题意;
C.
解:
是方程的解,不符合题意;
D.
解:
是方程的解,符合题意。
故答案为:D
32.D
【分析】可以把0.25化成0.5×0.5,也可以把0.25化成0.2+0.05;也可以把28化为7×4,也可以把28化为20+8;再根据乘法分配律,乘法结合律,进行解答。
【详解】A.28×0.25
=28×(0.5×0.5)
=28×0.5×0.5
所以28×0.25=28×0.5×0.5正确;
B.28×0.25
=28×(0.2+0.05)
=28×0.2+28×0.05
所以28×0.25=28×0.2+28×0.05正确;
C.28×0.25
=7×4×0.25
=7×(4×0.25)
所以28×0.25=7×(4×0.25)正确;
D.28×0.25
=(20+8)×0.25
=20×0.25+8×0.25
所以28×0.25=20×0.2+8×0.25错误。
计算28×0.25时,错误的方法是28×0.25=20×0.2+8×0.25。
故答案为:D
33.C
【分析】8.08×125可以将8.08拆分成8+0.08或8×1.01,再利用乘法分配律进行计算即可。
【详解】8.08×125
=8×1.01×125
=1.01×(8×125)
=1.01×1000
=1010
故答案为:C
【点睛】此题考查乘法分配律在小数乘法计算中的应用。
34.D
【分析】方程是指含有未知数的等式,所以方程必须具备两个条件:(1)含有未知数;(2)等式;由此进行解答。
【详解】A.81÷9=9,不含未知数,是等式,不是方程;
B.n+16,含有未知数,不是等式,不是方程;
C.4+a<56,含有未知数,不是等式,不是方程;
D.3m+0.8=3.2,含有未知数,是等式,是方程。
故答案为:D
35.C
【分析】根据乘法的意义,用2.1乘10求出已经装走的樱桃重量,再用30.8减去已经装走的重量,即可求出剩下的樱桃重量。求剩下的需要几个篮子来装,就是求剩下的重量里面有几个1.8千克,根据除法的意义,用剩下的重量除以1.8即可解答。结果需要用“进一法”取整数值。
【详解】(30.8-2.1×10)÷1.8
=(30.8-21)÷1.8
=9.8÷1.8
≈6(个)
则还需要6个篮子。
故答案为:C
36.D
【分析】把人民币2745元化成欧元数,用2745除以汇率9.15,即可得解。
【详解】2745÷9.45=300(欧元)
人民币2745元能兑换300欧元。
故答案为:D
【点睛】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
37.B
【分析】两个非0的因数相乘的积相等,一个因数越大,另一个因数越小,据此解答即可。
【详解】a×1.01=b×0.99,且a、b均不为0,
因为1.01>0.99,所以a<b,
故答案为:B
【点睛】明确两个非0的因数相乘的积相等,一个因数越大,另一个因数越小是解题的关键。
38.A
【分析】根据小数除法的计算方法进行计算,商用循环小数表示,找到循环节,即周期,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数格周期多n个,也就是余数是n,那么结果为下一个周期里的第n个。
【详解】1÷37=
60÷3=20(组)
1÷37的商,其小数点后面第60位上的数字是7。
故答案为:A
【点睛】关键是掌握循环小数的记数方法,会解决简单的周期问题。
39.A
【分析】从小数点后面第2位开始,每5位数字一循环,计算第2022位数字是第几组循环零几个数字,即可判断是多少。
【详解】(2022-1)÷5
=2021÷5
=404(组)……1(位)
余数是1,所以小数部分第2022位上的数字是4。
故答案为:A
【点睛】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
40.A
【分析】一个数(0除外)乘小于1的数,积比原来的数小。
【详解】如:a=0.1,5×a=5×0.1=0.5,0.5<5。
所以,若0<a<1,那么5×a所得的积小于5。
故答案为:A
【点睛】掌握不用计算判断积与因数之间大小关系的方法是解题的关键。
41.A
【分析】利用商不变的规律,看哪个除法算式的被除数和除数同时乘或除以相同的数(0除外)后,能变成27.3÷1.5,那么这两个算式的结果相同。
商不变的规律:被除数和除数同时乘(或除以)一个相同的数(0除外),商不变。
【详解】A.273÷15=(273÷10)÷(15÷10)=27.3÷1.5
所以,273÷15与27.3÷1.5结果相同;
B.2.73÷1.5=(2.73×10)÷(1.5×10)=27.3÷15
27.3÷15≠27.3÷1.5,所以2.73÷1.5与27.3÷1.5结果不相同;
C.2.73÷15=(2.73×10)÷(15×10)=27.3÷150
27.3÷150≠27.3÷1.5,所以2.73÷15与27.3÷1.5结果不相同。
故答案为:A
42.C
【分析】根据单价×数量=总价,路程=速度×时间,倍数的含义,长方形的面积=长×宽,即可解答。
【详解】A.1千克樱桃43.4元,买0.8千克要花多少钱,列式:43.4×0.8,符合题意;
B.一辆汽车的速度是43.4千米/时,0.8小时行多少千米,列式:43.4×0.8,符合题意;
C.甲数是43.4,它是乙数的0.8倍,乙数是多少,列式:43.4÷0.8,不符合题意;
D.一个长方形的长是43.4米,宽是0.8米,它的面积是多少,列式:43.4×0.8,符合题意。
故答案为:C
【点睛】本题考查了利用小数乘除法解决问题,需准确分析各选项中的数量关系,准确解答。
43.C
【分析】把平行四边形拉成长方形后,四条边的长度没变,所以周长不变,但对应底上的高变长了,平行四边形和长方形的面积都等于底乘高,当底不变,高变大,则面积变大了;据此解答。
【详解】如图:
把一个平行四边形拉成一个长方形后,周长不变,底边长不变,它的高变大了,所以面积变大。
故答案为:C
【点睛】此题主要考查平行四边形的特征以及平行四边形、长方形面积公式的综合应用。
44.B
【分析】明确数对的概念:数对是一个表示位置的概念,相当于坐标,前一个数字表示列,后一个数字表示行。分析棋子的位置:已知棋子A的位置记作(1,4),说明第1列第4行。确定黑棋子获胜的位置:观察棋盘,黑棋子在第4行已经有4个棋子,再在第6列第4行放一个棋子,就能形成5个连续的棋子,从而获胜。
【详解】棋子A在(1,4),表示第1列第4行。黑棋子在第4行已有4个,在(6,4)位置放棋子可形成5连。
故答案为:B
45.C
【分析】含有未知数的等式叫做方程,可据此逐项分析,再做选择即可。
【详解】A.12÷4+10,这可以看作一个算式,但没有算出结果,不是方程;
B.5.2-2×1.1=3,这是一个等式,不含有未知数,不是方程;
C.4.5x-5=4,这是一个含有未知数的等式,是方程;
D.x-2<5,这个式子含有未知数,但不是等式,不是方程。
这些式子中,4.5x-5=4是方程。
故答案为:C
【点睛】需要明确方程的含义,一方面需要含有字母,即未知数;同时还得是等式;二者缺一不可。
46.B
【分析】根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行;明明坐在小强正后方第一个位置上,则明明与小强在同一列,用小强的行数加1即是明明的行数。
【详解】3+1=4
则明明坐在小强正后方第一个位置上,明明的位置用数对表示是(4,4)。
故答案为:B
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
47.A
【分析】用香油的总质量除以一个瓶子最多可以装的质量,利用“进一法”即可求出至少需要准备几个这样的瓶子。
【详解】2.9÷0.7≈4.1≈5(个)
则妈妈至少需要准备5个这样的瓶子。
故答案为:A
48.A
【分析】一个数(0除外)乘大于1的数,积比原来的数大。
因为1.54>1,所以9.□×1.54>9.□;因为9.□×2≥18,所以9.□<9.□×1.54<18;比较四个选项中的积,在9.□~18范围内的,就是9.□×1.54正确的积。
【详解】1<1.54<2,所以9.□<9.□×1.54<18;
A.9.□<14.63<18,符合题意;
B.1.463<9.□,不符合题意;
C.146.3>18,不符合题意;
D.0.1463<9.□,不符合题意;
不计算9.□×1.54正确的积是14.63。
故答案为:A
【点睛】掌握判断积与因数之间大小关系的方法是解题的关键。
49.D
【分析】根据方程的意义:含有未知数的等式叫做方程,方程具备两个条件:一含有未知数,二必须是等式,据此解答。
【详解】A.7x-2>12,含有未知数,不是等式,不是方程;
B.12+8=20,是等式,不含有未知数,不是方程;
C.1.5a+2.3,含有未知数,不是等式,不是方程;
D.39-3a=3,含有未知数,是等式,是方程。
故答案为:D
50.A
【分析】把长方形拉成平行四边形,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形底边的邻边,则长方形周长等于平行四边形的周长,比较长方形的宽和平行四边形高的大小关系,即可求得长方形的面积和平行四边形面积的大小关系,据此解答。
【详解】
长方形的周长=(长+宽)×2
平行四边形的周长=(底边+邻边)×2
由图可知,长方形的长等于平行四边形的底,宽等于平行四边形底边的邻边,因此周长不变。
长方形的面积=长×宽
平行四边形的面积=底×高
由图可知,把长方形拉成平行四边形,随着拉动,高逐渐变小,但底不变。
因此面积变小了。
故答案为:A
【点睛】分析长方形的宽和平行四边形的高的大小关系是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
