河南省商丘市2024-2025学年高一下学期期末考试数学(B)试卷(图片版,含解析)
文档属性
| 名称 | 河南省商丘市2024-2025学年高一下学期期末考试数学(B)试卷(图片版,含解析) |
|
|
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 00:00:00 | ||
图片预览




文档简介
2024~2025学年度高一下学期期末联考试卷
数
学
考生注意:
1.本试卷分选择题和非选择题两部分。满分150分,考试时间120分钟。
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的
答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,
超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
4.本卷命题范固:人教A版必修第二册。
一、选择题:本题共8小题,每小题5分,共0分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知复数x满足(1一i)x=2i,则z的虚部为
A.-1
B.1
C.-i
D.i
2.某羽毛球俱乐部有A队和B队,其中A队有80名学员,B队有60名学员,为了解俱乐部学员的羽毛
球水平,用比例分配的分层随机抽样的方法从该俱乐部中抽取一个容量为m的样本,已知从B队中抽
取了15名学员,则m的值为
A.30
B.25
C.40
D.35
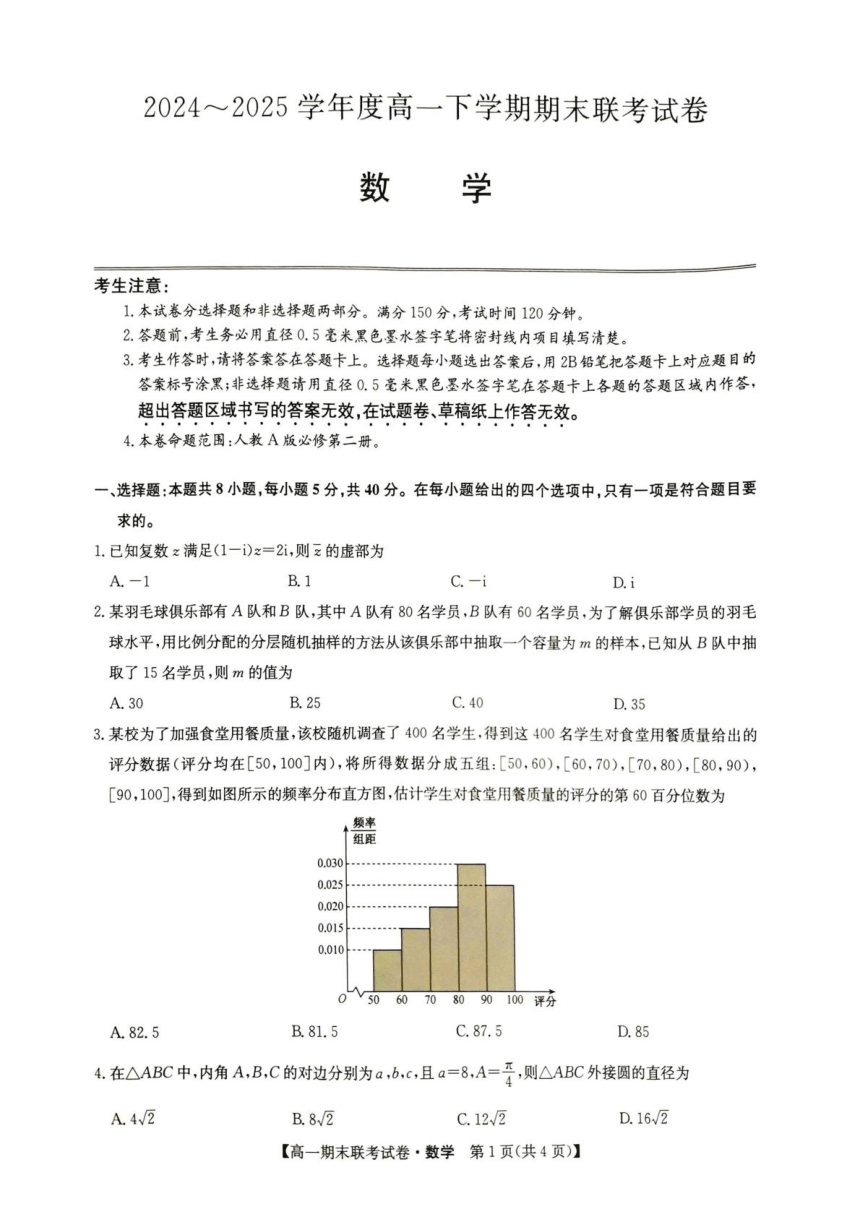
3.某校为了加强食堂用餐质量,该校随机调查了400名学生,得到这400名学生对食堂用餐质量给出的
评分数据(评分均在[50,100]内),将所得数据分成五组:[50,60),[60,70),[70,80),[80,90),
[90,100],得到如图所示的频率分布直方图,估计学生对食堂用餐质量的评分的第60百分位数为
须率
组距
0.030
0.02
0.020
0.015
0.010
0V506070809010评分
A.82.5
B.81.5
C.87.5
D.85
4.在△ABC中,内角A,B,C的对边分别为a,6:c,且a=8,A=,则△ABC外接圆的直径为
A.42
B.82
C.122
D.162
【高一期末联考试卷·数学第1页(共4页)】
5.已知m,n是两条不同的直线,a表示平而,且m⊥a,则“n∥a”是“n⊥n”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
6.记△ABC的内角A,B,C的对边分别为a,bc,且白cosC+后cOsB=inA,则△ABC是
A直角三角形
B.锐角三角形
C.等边三角形
D.钝角三角形
7.已知一个圆锥和圆柱的底面半径和侧面积分别相等,且圆锥的轴截面是等边三角形,则这个圆锥和圆
柱的体积之比为
A号
B.√2
c
D.3
8.已知正方形ABCD的边长为3,点E是边BC上的一点,且CE=2EB,点P是边DC上的一点,则
A户.EP的最小值为
A胃
B号
C.15
D
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得6分,部分选对的得部分分,有选错的得0分。
9.在△ABC中,内角A,B,C的对边分别为a,bc,且B=,a=6,b=2,则c的可能取值为
A.3
B.√2
C.2√2
D.23
10.已知一组数据x1x2x,x,x5,x6,x,(x15,6,7)生成的一组新数据,2,yy4yy%,y,则
A新数据的极差可能与原数据的极差相等
B.新数据的平均数可能与原数据的平均数相等
C.新数据的中位数一定比原数据的中位数大
D.新数据的标准差一定比原数据的标准差大
11.在直三棱柱ABC-A1B,C1中,AA1=3,AB=BC=2,AC=2√2,点M是棱BB1上的一点,则下列说
法正确的是
A.AM⊥BC
B.四棱锥M-ACC1A1的体积为2
C.直三棱柱ABC-A,B,C1外接球的表面积是17π
D.MA1+MC的最小值为5
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量a,b的夹角为,a=5,b1=4,则(3a+b)·b=
13.从分别写有1,2,3,4,5的5张卡片中不放回地随机抽取3张,则抽到的3张卡片上的数字之和不小
于10的概率为
14.在棱长为2的正方体ABCD-A,B,CD,中,点E是棱DD,的中点,则直线A,E与AC所成角的余
弦值为
;点P是正方体表面上的一动点,且满足EP⊥AC,则动点P的轨迹长度是
【高一期末联考试卷·数学第2页(共4页)】
数
学
考生注意:
1.本试卷分选择题和非选择题两部分。满分150分,考试时间120分钟。
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的
答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,
超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
4.本卷命题范固:人教A版必修第二册。
一、选择题:本题共8小题,每小题5分,共0分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知复数x满足(1一i)x=2i,则z的虚部为
A.-1
B.1
C.-i
D.i
2.某羽毛球俱乐部有A队和B队,其中A队有80名学员,B队有60名学员,为了解俱乐部学员的羽毛
球水平,用比例分配的分层随机抽样的方法从该俱乐部中抽取一个容量为m的样本,已知从B队中抽
取了15名学员,则m的值为
A.30
B.25
C.40
D.35
3.某校为了加强食堂用餐质量,该校随机调查了400名学生,得到这400名学生对食堂用餐质量给出的
评分数据(评分均在[50,100]内),将所得数据分成五组:[50,60),[60,70),[70,80),[80,90),
[90,100],得到如图所示的频率分布直方图,估计学生对食堂用餐质量的评分的第60百分位数为
须率
组距
0.030
0.02
0.020
0.015
0.010
0V506070809010评分
A.82.5
B.81.5
C.87.5
D.85
4.在△ABC中,内角A,B,C的对边分别为a,6:c,且a=8,A=,则△ABC外接圆的直径为
A.42
B.82
C.122
D.162
【高一期末联考试卷·数学第1页(共4页)】
5.已知m,n是两条不同的直线,a表示平而,且m⊥a,则“n∥a”是“n⊥n”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
6.记△ABC的内角A,B,C的对边分别为a,bc,且白cosC+后cOsB=inA,则△ABC是
A直角三角形
B.锐角三角形
C.等边三角形
D.钝角三角形
7.已知一个圆锥和圆柱的底面半径和侧面积分别相等,且圆锥的轴截面是等边三角形,则这个圆锥和圆
柱的体积之比为
A号
B.√2
c
D.3
8.已知正方形ABCD的边长为3,点E是边BC上的一点,且CE=2EB,点P是边DC上的一点,则
A户.EP的最小值为
A胃
B号
C.15
D
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得6分,部分选对的得部分分,有选错的得0分。
9.在△ABC中,内角A,B,C的对边分别为a,bc,且B=,a=6,b=2,则c的可能取值为
A.3
B.√2
C.2√2
D.23
10.已知一组数据x1x2x,x,x5,x6,x,(x1
A新数据的极差可能与原数据的极差相等
B.新数据的平均数可能与原数据的平均数相等
C.新数据的中位数一定比原数据的中位数大
D.新数据的标准差一定比原数据的标准差大
11.在直三棱柱ABC-A1B,C1中,AA1=3,AB=BC=2,AC=2√2,点M是棱BB1上的一点,则下列说
法正确的是
A.AM⊥BC
B.四棱锥M-ACC1A1的体积为2
C.直三棱柱ABC-A,B,C1外接球的表面积是17π
D.MA1+MC的最小值为5
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量a,b的夹角为,a=5,b1=4,则(3a+b)·b=
13.从分别写有1,2,3,4,5的5张卡片中不放回地随机抽取3张,则抽到的3张卡片上的数字之和不小
于10的概率为
14.在棱长为2的正方体ABCD-A,B,CD,中,点E是棱DD,的中点,则直线A,E与AC所成角的余
弦值为
;点P是正方体表面上的一动点,且满足EP⊥AC,则动点P的轨迹长度是
【高一期末联考试卷·数学第2页(共4页)】
同课章节目录
