2.2对数函数
图片预览
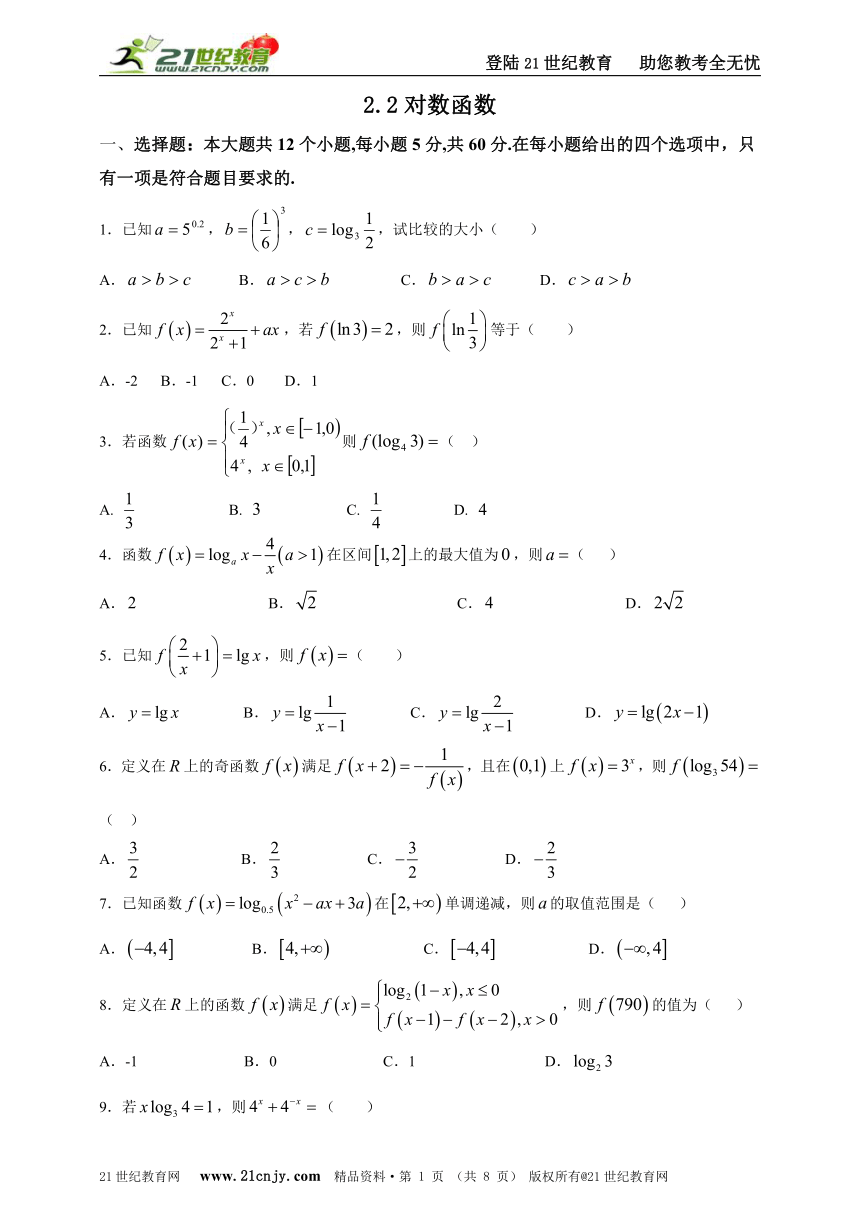



文档简介
2.2对数函数
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.www.21-cn-jy.com
1.已知,,,试比较的大小( )
A. B. C. D.
2.已知,若,则等于( )
A.-2 B.-1 C.0 D.1
3.若函数则( )
A. B. C. D.
4.函数在区间上的最大值为,则( )
A. B. C. D.
5.已知,则( )
A. B. C. D.
6.定义在上的奇函数满足,且在上,则( )
A. B. C. D.
7.已知函数在单调递减,则的取值范围是( )
A. B. C. D.
8.定义在上的函数满足,则的值为( )
A.-1 B.0 C.1 D.
9.若,则( )
A. B. C. D.
10.函数 在为减函数,则a的范围( )
A. B.(- ,-4) C. D.
11.函数的单调递减区间是( )
A. B. C. D.
12.设定义在区间上的函数是奇函数且,则的取值范围是( )
A. B. C. D.
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.函数的定义域是 .
14.已知函数
15.设,则__________.(其中为自然对数的底数)
16.函数是函数的反函数,则函数的图象过定点 .
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(1)求值
(2)已知,求的值.
18.已知函数.
(I)当时,求函数的定义域;
(II)若关于的不等式的解集是,求的取值范围.
19.已知函数
(1)判断函数的奇偶性;
(2)用定义判断函数的单调性.
20.已知函数.
(1)若,求不等式的解集;
(2)若为偶函数,求的值.
21.已知函数.
(1)若函数的值域为,求实数的取值范围;
(2)当时,函数恒有意义,求实数的取值范围.
22.已知函数,且.
(1)若,求实数的取值范围;
(2)求使成立的的值.
2.2对数函数参考答案及解析
1.A【解析】因为,,,所以,故选A.
2.B【解析】设,可证是奇函数,,则,所以,.故选B.
3.B【解析】由,则 .
4.B【解析】因为,所以在区间上递增,可得的最大值为,解得,故选B.
5.C【解析】令,则,即,选C.
6.B【解析】由题意可得,即函数是周期为4的周期函数,又是上的奇函数,在上,故
7.C【解析】对数的底0.5∈(0,1),得相应的对数函数是减函数,由此得是区间[2,+∞)上的增函数,且在[2,+∞)上t>0总成立,建立关于a的不等式并解之,可得a的取值范围.令,∵0.5∈(0,1),∴函数y=log0.5t是关于t的减函数结合题意,得是区间[2,+∞)上的增函数,又∵在(2,+∞)上t>0总成立,,故选C.21世纪教育网版权所有
8.C【解析】由于x>0时,f(x)=f(x-1)-f(x-2),将x换为x+1,得到f(x+1)=-f(x-2),再将x换为x+2,再将x换为x+3得到f(x+6)=f(x),化简f(790)=-f(1),由x≤0的表达式,即可求出.x>0时,f(x)=f(x-1)-f(x-2),将x换为x+1,得f(x+1)=f(x)-f(x-1),则f(x+1)=-f(x-2),再将x换为x+2,得f(x+3)=-f(x),再将x换为x+3,得f(x+6)=-f(x+3)=f(x),则f(790)=f(131×6+4)=f(4)=-f(1)=1故选C.21教育网
9.D【解析】,
从而
10.C【解析】由因为在定义域上为减函数,且复合函数在上为减函数,所以在上必为增函数,所以故选C.21cnjy.com
11.D【解析】由得或,原函数由复合而成,是减函数,在时递减,在时递增,所以复合函数的递减区间为21·cn·jy·com
12.A【解析】∵定义在区间上的函数是奇函数∴f(-x)+f(x)=0
,∵a≠-2∴a=2
∴令,可得,∴∵a=2,∴的取值范围是
13. 【解析】由,则:。解得;, 再加周期得:
14.4【解析】
15.【解析】.
16.【解析】由题:过定点为: ,由反函数的性质得:则函数的图象过定点.
17.【解析】(1);
(2)或(舍去),
.
18.【解析】 (Ⅰ)当时,函数的定义域即为不等式的解集.
由于,或, 或.
所以,无解,或.
综上,函数的定义域为
(Ⅱ)若使的解集是,则只需恒成立.
由于,
所以的取值范围是.
19.【解析】(1)
又
为奇函数
(2)设
∵
又
从而故在上为减函数.
20.【解析】(1),,
,即不等式的解集为.
(2)由于为偶函数,∴即,
对任意实数都成立,
所以
考点:1.函数奇偶性的性质;2.对数函数图象与性质的综合应用
21. 【解析】(1)令,由题设知需取内的任意值,所以,解得,又,且.
所以的取值范围是.
(2)由题意知对一切恒成立且,,
即对一切恒成立,
令,当时,
取得最小值,
则,又因为,,
所以的取值范围为.
22.【解析】
(1)由,可得函数在定义域上单调递增,所以可得: ,解得;
(2)因为,可得,解得.
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.www.21-cn-jy.com
1.已知,,,试比较的大小( )
A. B. C. D.
2.已知,若,则等于( )
A.-2 B.-1 C.0 D.1
3.若函数则( )
A. B. C. D.
4.函数在区间上的最大值为,则( )
A. B. C. D.
5.已知,则( )
A. B. C. D.
6.定义在上的奇函数满足,且在上,则( )
A. B. C. D.
7.已知函数在单调递减,则的取值范围是( )
A. B. C. D.
8.定义在上的函数满足,则的值为( )
A.-1 B.0 C.1 D.
9.若,则( )
A. B. C. D.
10.函数 在为减函数,则a的范围( )
A. B.(- ,-4) C. D.
11.函数的单调递减区间是( )
A. B. C. D.
12.设定义在区间上的函数是奇函数且,则的取值范围是( )
A. B. C. D.
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.函数的定义域是 .
14.已知函数
15.设,则__________.(其中为自然对数的底数)
16.函数是函数的反函数,则函数的图象过定点 .
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.(1)求值
(2)已知,求的值.
18.已知函数.
(I)当时,求函数的定义域;
(II)若关于的不等式的解集是,求的取值范围.
19.已知函数
(1)判断函数的奇偶性;
(2)用定义判断函数的单调性.
20.已知函数.
(1)若,求不等式的解集;
(2)若为偶函数,求的值.
21.已知函数.
(1)若函数的值域为,求实数的取值范围;
(2)当时,函数恒有意义,求实数的取值范围.
22.已知函数,且.
(1)若,求实数的取值范围;
(2)求使成立的的值.
2.2对数函数参考答案及解析
1.A【解析】因为,,,所以,故选A.
2.B【解析】设,可证是奇函数,,则,所以,.故选B.
3.B【解析】由,则 .
4.B【解析】因为,所以在区间上递增,可得的最大值为,解得,故选B.
5.C【解析】令,则,即,选C.
6.B【解析】由题意可得,即函数是周期为4的周期函数,又是上的奇函数,在上,故
7.C【解析】对数的底0.5∈(0,1),得相应的对数函数是减函数,由此得是区间[2,+∞)上的增函数,且在[2,+∞)上t>0总成立,建立关于a的不等式并解之,可得a的取值范围.令,∵0.5∈(0,1),∴函数y=log0.5t是关于t的减函数结合题意,得是区间[2,+∞)上的增函数,又∵在(2,+∞)上t>0总成立,,故选C.21世纪教育网版权所有
8.C【解析】由于x>0时,f(x)=f(x-1)-f(x-2),将x换为x+1,得到f(x+1)=-f(x-2),再将x换为x+2,再将x换为x+3得到f(x+6)=f(x),化简f(790)=-f(1),由x≤0的表达式,即可求出.x>0时,f(x)=f(x-1)-f(x-2),将x换为x+1,得f(x+1)=f(x)-f(x-1),则f(x+1)=-f(x-2),再将x换为x+2,得f(x+3)=-f(x),再将x换为x+3,得f(x+6)=-f(x+3)=f(x),则f(790)=f(131×6+4)=f(4)=-f(1)=1故选C.21教育网
9.D【解析】,
从而
10.C【解析】由因为在定义域上为减函数,且复合函数在上为减函数,所以在上必为增函数,所以故选C.21cnjy.com
11.D【解析】由得或,原函数由复合而成,是减函数,在时递减,在时递增,所以复合函数的递减区间为21·cn·jy·com
12.A【解析】∵定义在区间上的函数是奇函数∴f(-x)+f(x)=0
,∵a≠-2∴a=2
∴令,可得,∴∵a=2,∴的取值范围是
13. 【解析】由,则:。解得;, 再加周期得:
14.4【解析】
15.【解析】.
16.【解析】由题:过定点为: ,由反函数的性质得:则函数的图象过定点.
17.【解析】(1);
(2)或(舍去),
.
18.【解析】 (Ⅰ)当时,函数的定义域即为不等式的解集.
由于,或, 或.
所以,无解,或.
综上,函数的定义域为
(Ⅱ)若使的解集是,则只需恒成立.
由于,
所以的取值范围是.
19.【解析】(1)
又
为奇函数
(2)设
∵
又
从而故在上为减函数.
20.【解析】(1),,
,即不等式的解集为.
(2)由于为偶函数,∴即,
对任意实数都成立,
所以
考点:1.函数奇偶性的性质;2.对数函数图象与性质的综合应用
21. 【解析】(1)令,由题设知需取内的任意值,所以,解得,又,且.
所以的取值范围是.
(2)由题意知对一切恒成立且,,
即对一切恒成立,
令,当时,
取得最小值,
则,又因为,,
所以的取值范围为.
22.【解析】
(1)由,可得函数在定义域上单调递增,所以可得: ,解得;
(2)因为,可得,解得.
