【章节考点培优】2.1代数式-2025-2026学年七年级上册数学沪科版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】2.1代数式-2025-2026学年七年级上册数学沪科版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 254.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 11:52:54 | ||
图片预览



文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优沪科版(2024)
第2章 整式及其加减 2.1 代数式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
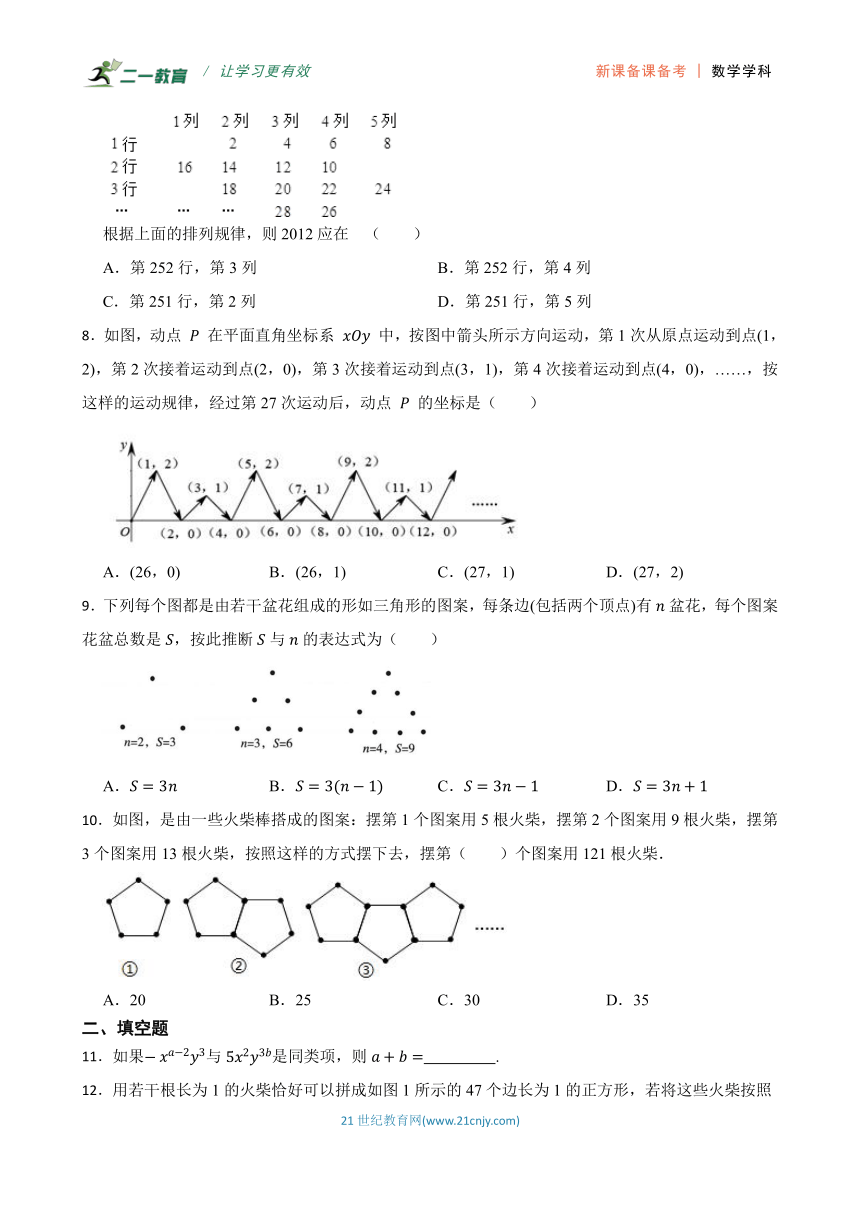
1.已知代数式的值是1,则代数式的值是( )
A.1 B. C.2 D.
2.下列各式中:①;②;③;④;⑤;⑥0,是代数式的为( )
A.①③④⑤ B.①③④⑥ C.①④⑤⑥ D.①②⑤⑥
3.若a、b是两个连续整数,且a<<b,则a+b的值为( )
A.6 B.7 C.8 D.9
4.已知,则的值为( )
A.0 B.1 C. D.2
5.定义新运算:p q= ,例如:3 5= ,3 (﹣5)= ,则y=2 x(x≠0)的图象是( )
A. B.
C. D.
6.已知a-b=3,b+c=-5,则代数式ac-bc+a2-ab的值为 ( )
A.一15 B.一2 C.一6 D.6
7.将正偶数如图所示排成5列:
根据上面的排列规律,则2012应在 ( )
A.第252行,第3列 B.第252行,第4列
C.第251行,第2列 D.第251行,第5列
8.如图,动点 在平面直角坐标系 中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点 的坐标是( )
A.(26,0) B.(26,1) C.(27,1) D.(27,2)
9.下列每个图都是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有盆花,每个图案花盆总数是,按此推断与的表达式为( )
A. B. C. D.
10.如图,是由一些火柴棒搭成的图案:摆第1个图案用5根火柴,摆第2个图案用9根火柴,摆第3个图案用13根火柴,按照这样的方式摆下去,摆第( )个图案用121根火柴.
A.20 B.25 C.30 D.35
二、填空题
11.如果与是同类项,则 .
12.用若干根长为1的火柴恰好可以拼成如图1所示的47个边长为1的正方形,若将这些火柴按照如图2所示的方式拼,则可以拼出 个边长为1的正方形.
13.若一元二次方程的两个实数根分别是3、b, 则 .
14.如图,两个正方形边长分别为a、b,如果,,则阴影部分的面积为 .
15.把如图所示的图形折叠成一个正方体的盒子,折好后相对面上的数互为相反数,则 .
16.已知x、y、z为有理数,且|x+y+z+1|=x+y﹣z﹣2,则 = .
三、计算题
17.化简求值:,其中,.
四、解答题
18.已知 ,且2x+y+3z≠0,求 的值.
19.如图,某社区在一块长和宽分别为(x+2y)m,(2x+y) m的长方形空地上划出两块大小相同的边长为ym的正方形区域种植花草(数据如图所示,单位m,留下一块”T”型区域建休闲广场(阴影部分).
(1)用含x,y的式子表示休闲广场的面积并化简;
(2)若|y-5|+(x-2)2=0,请计算休闲广场的面积.
20.数a在数轴上的位置如图,且|a+1|=2,求|3a+7|.
21.列式表示:
(1)比a的一半大3的数; (2)a与b的差的c倍; (3)a与b的倒数的和; (4)a与b的和的平方的相反数.
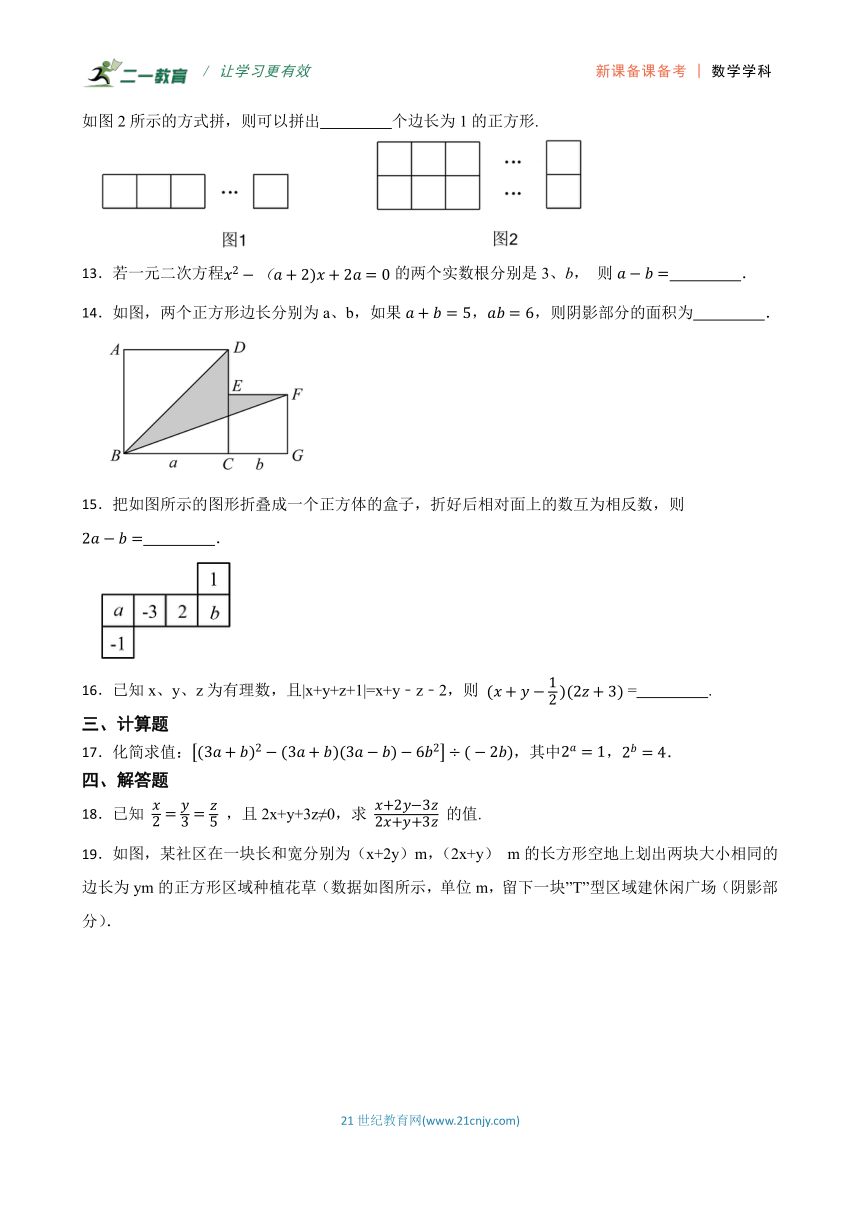
22.某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每个定价50元,厂方开展促销活动期间,可以同时向客户提供两种优惠方案:
方案一:买一台饮水机送一个饮水机桶;
方案二:饮水机和饮水机桶都按定价的九折付款.
现某客户到该饮水机厂购买饮水机20台,饮水机桶x(超过20)个.
(1)若该客户按方案一购买,求客户需付款钱数(用含x的式子表示);
若该客户按方案二购买,求客户需付款钱数(用含x的式子表示).
(2)若x=50,通过计算说明此时客户按哪种方案购买较合算.
(3)当x=50时,你还能给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出所需的钱数.
23.问题情境:如图,,定点E,F分别在直线,上,在平行线,之间有一个动点P,满足.求,,满足的数量关系.
思路点拨:由于点P是平行线,之间一动点,因此需对点P的位置进行分类讨论,过点P作的平行线,通过平行线的性质推出,,的数量关系.
(1)问题解决:如图1,当点P在的左侧时,写出,,满足的数量关系_____;如图2,当点P在的右侧时,写出,,满足的数量关系______.
(2)问题迁移:如图3,、分别平分和,且点P在左侧.
①若,则的度数为_______;
②猜想与的数量关系,并说明理由;
(3)问题拓展:如图4,若与的角平分线交于点,与的角平分线交于点,与的角平分线交于点,以此类推,直接写出与满足的数量关系.
参考答案及试题解析
1.C
2.C
3.B
【解答】解:∵9<11<16,
∴且3<<4,
∵a<<b,a、b是两个连续整数,
∴a=3,b=4,
∴a+b=3+4=7,
故选:B.
【分析】本题考查了无理数的大小估值,由9<11<16,得到3<<4,结合a、b是两个连续整数,求得a和b的值,将其代入代数式 a+b ,计算求值,即可得到答案.
4.B
5.D
【解答】解:∵p q= ,
∴y=2 x= 。
故答案为:D。
【分析】根据新定义运算的法则写出函数关系式,再根据所得函数的性质、图象与系数的关系即可得出答案。
6.C
【分析】首先将a-b=3、b+c=-5两式等号左右两边分别相加,得到a+c的值;再将代数式ac-bc+a2-ab分解因式转化为(a-b)(a+c);最后将a-b、a+c做为一个整体代入求得代数式的结果。
【解答】∵a-b=3,b+c=-5
∴a-b+b+c=3-5,解a+c=-2
∴ac-bc+a2-ab=c(a-b)+a(a-b)=(a-b)(a+c)=3×(-2)=-6
故选C
【点评】本题考查因式分解的应用、代数式求值.解决本题的关键是将a-b、b+c、a+c做为一个整体来应用。
7.A
【解答】∵2012÷2=1006∴2012是第1006个偶数,而1006÷4=251…2,
∴第1006个偶数在第252行,偶数行的数从第4列开始前面排,∴第1006个偶数在第3列,∴2012应在第252行第三列.
故答案为:A.
【分析】根据题意,找到规律即可作答。
8.C
【解答】由图可归纳出以下两条规律:(n为正整数)(1)第n次运动后,动点P的横坐标为n(2)在运动过程中,动点P的纵坐标是以 为循环变换的
则经过第27次运动后,动点 的横坐标为27
经过第27次运动后,动点 的纵坐标与第3次运动后,动点 的纵坐标相同,即为1
综上,所求的动点P的坐标是
故答案为:C.
【分析】根据图形中前几次运动后,动点P的坐标,归纳类推出规律,由此即可得出答案.
9.B
【解答】解:由图可知:
第一图:有花盆3个,每条边有2盆花,那么3=3×(2-1);
第二图:有花盆6个,每条边有3盆花,那么6=3×(3-1);
第三图:有花盆9个,每条边有4盆花,那么9=3×(4-1);
…
由此可知S与n的关系式为S=3(n-1).
故答案为:B.
【分析】根据题意找出规律得出S=3n-3,即可求解.
10.C
【解答】解:观察图形,得
图①用了5根火柴,即5=1×4+1,
图②用了9根火柴,即9=2×4+1,
图③用了13根火柴,即13=3×4+1,
…
图n用了(4n+1)根火柴,
根据题意得:4n+1=121,
解得n=30,
所以摆第,30个图案用121根火柴棒.
故答案为:C.
【分析】先找出规律求出图n用了(4n+1)根火柴,再求出4n+1=121,最后计算求解即可。
11.5
12.56
【解答】解:由图1得火柴根数
令则
由图2得火柴根数,
∴
∴正方形个数为:
故答案为:56.
【分析】由图1得火柴根数令求出火柴根数,根据图2得火柴根数,列方程即可求解.
13.1
【解答】解:∵一元二次方程的两个实数根分别是3、b
∴,解得:
∴
故答案为:1
【分析】根据二次方程中根与系数的关系列出方程组,解方程组可得a,b值,再代入代数式即可求出答案.
14.
15.
16.0
【解答】∵|x+y+z+1|=x+y+z+1或|x+y+z+1|=-(x+y+z+1),
∴x+y+z+1=x+y-z-2或-(x+y+z+1)=x+y-z-2,
∴z=- 或x+y= ,
当z=- 时,(x+y )(2z+3)=(x+y- )[2×(- )+3]=0;
当x+y= 时,(x+y )(2z+3)=( - )(2z+3)=0,
综上所述,(x+y )(2z+3)的值为0.
故答案为:0.
【分析】根据绝对值的意义可得|x+y+z+1|=x+y+z+1或|x+y+z+1|=-(x+y+z+1),从而可得x+y+z+1=x+y-z-2或-(x+y+z+1)=x+y-z-2,解得z=- 或x+y= ,然后将其分别代入原式中计算即可.
17.,4
18.解:∵ ,
∴x= y,z= y,
∴ =
【分析】由已知条件可得x=y,z=y,然后代入待求式中进行化简即可.
19.(1)解:由题意可得:
大长方形的面积为:(x+2y)(2x+y)m2
两正方形面积为:(2y2)m2
则休闲广场的面积为:
(x+2y)(2x+y)-2y2
=2x2+4xy+xy+2y2-2y2
=(2x2+5xy)m2
(2)解:由题意可得:
y-5=0,x-2=0
解得:y=5,x=2
则休闲广场的面积为:2×22+5×2×5=58m2
【分析】(1)根据休闲广场的面积=大长方形的面积-两小正方形的面积,列出代数式并化简即可求出答案.
(2)根据绝对值和偶次幂的非负性可求出x,y值,再代入(1)代数式即可求出答案.
20.解:∵|a+1|=2
∴a+1=2或-2
∴a=1或-3
当a=1时,|3a+7|=|3×1+7|=10
当a=-3时,|3a+7|=|3×(-3)+7|=2
【分析】 根据|a+1|=2, 结合绝对值的非负性求出a的值,然后分情况把a值代入 |3a+7| 求值即可.
21.(1 );(2)(a-b)c;(3)a+;(4)-(a+b)2
【解答】(1);(2)(a-b)c;(3)a+;(4)-(a+b)2
【分析】把问题中与数量有关的词语用含有数、字母和运算符号的式子表示出来就是列代数式;注意要弄清与运算有关词语的意义以及问题中“的”字处得运算的先后顺序.
22.(1)解:客户按方案一.购买需付款20×350+ (x-20) ×50=50x+20×(350-50)=(50x+6000)元;
客户按方案二购买需付款350×90%×20 + 50.×90%×x=(45x+6 300)元.
(2)解:当x=50时,
按方案一购买,需20×350+ (50- 20) ×50=8 500(元);
按方案二购买,需350×90%×20+ 50×90%×50=8 550(元).
所以按方案一购买合算.
(3)解:更为省钱的购买方案:按方案一购买20台饮水机,按方案二购买30个饮水机桶.
按方案一购买20台饮水机,送20个饮水机桶,需20×350=7 000(元),
按方案二购买30个饮水机桶,需50×90%×30=1350(元),
7 000+1 350=8 350(元),
故共需8 350元.
【分析】(1)按照对应的方案的计算方法分别列出代数式即可;
(2)把x = 50代入求得的代数式求得数值,进一步比较得出答案即可;
(3)根据两种方案的优惠方式,可得出先按方案一购买20台饮水机,送20只饮水机桶,另外30只饮水机桶再按方案二购买即可.
23.(1),.
(2)解:①
②如图3,,分别平分和,
设:,
,
则
,
,
即:.
(3)
【解答】(1)解:①当点P在的左侧时,
如图,过点P作,
,
,
,
,
;
②当点P在的右侧时,
如图,过点P作,
,
,
,
,
;
故答案为:;;
(2)解:①由(1)知,
,
,分别平分和,
,
,
,
,
,
故答案为;
(3)解:同理可得,
,
,
∴.
故答案为:.
【分析】(1)分类讨论:①当点P在的左侧时,②当点P在的右侧时,先分别画出图形并利用角的运算和等量代换求解即可;
(2)①利用角平分线的定义及角的运算和等量代换求出即可;
②先利用角平分线的定义及角的运算求出即可;
(3)先求出,,再求出即可.
(1)解:当点P在的左侧时,
如图,过点P作,
,
,
,
,
;
当点P在的右侧时,
如图,过点P作,
,
,
,
,
;
故答案为:,
;
(2)解:①由(1)知,
,
,分别平分和,
,
,
,
,
,
故答案为;
②如图3,,分别平分和,
设:,
,
则
,
,
即:;
(3)解:同理可得,
,
,
故:.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优沪科版(2024)
第2章 整式及其加减 2.1 代数式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知代数式的值是1,则代数式的值是( )
A.1 B. C.2 D.
2.下列各式中:①;②;③;④;⑤;⑥0,是代数式的为( )
A.①③④⑤ B.①③④⑥ C.①④⑤⑥ D.①②⑤⑥
3.若a、b是两个连续整数,且a<<b,则a+b的值为( )
A.6 B.7 C.8 D.9
4.已知,则的值为( )
A.0 B.1 C. D.2
5.定义新运算:p q= ,例如:3 5= ,3 (﹣5)= ,则y=2 x(x≠0)的图象是( )
A. B.
C. D.
6.已知a-b=3,b+c=-5,则代数式ac-bc+a2-ab的值为 ( )
A.一15 B.一2 C.一6 D.6
7.将正偶数如图所示排成5列:
根据上面的排列规律,则2012应在 ( )
A.第252行,第3列 B.第252行,第4列
C.第251行,第2列 D.第251行,第5列
8.如图,动点 在平面直角坐标系 中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点 的坐标是( )
A.(26,0) B.(26,1) C.(27,1) D.(27,2)
9.下列每个图都是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有盆花,每个图案花盆总数是,按此推断与的表达式为( )
A. B. C. D.
10.如图,是由一些火柴棒搭成的图案:摆第1个图案用5根火柴,摆第2个图案用9根火柴,摆第3个图案用13根火柴,按照这样的方式摆下去,摆第( )个图案用121根火柴.
A.20 B.25 C.30 D.35
二、填空题
11.如果与是同类项,则 .
12.用若干根长为1的火柴恰好可以拼成如图1所示的47个边长为1的正方形,若将这些火柴按照如图2所示的方式拼,则可以拼出 个边长为1的正方形.
13.若一元二次方程的两个实数根分别是3、b, 则 .
14.如图,两个正方形边长分别为a、b,如果,,则阴影部分的面积为 .
15.把如图所示的图形折叠成一个正方体的盒子,折好后相对面上的数互为相反数,则 .
16.已知x、y、z为有理数,且|x+y+z+1|=x+y﹣z﹣2,则 = .
三、计算题
17.化简求值:,其中,.
四、解答题
18.已知 ,且2x+y+3z≠0,求 的值.
19.如图,某社区在一块长和宽分别为(x+2y)m,(2x+y) m的长方形空地上划出两块大小相同的边长为ym的正方形区域种植花草(数据如图所示,单位m,留下一块”T”型区域建休闲广场(阴影部分).
(1)用含x,y的式子表示休闲广场的面积并化简;
(2)若|y-5|+(x-2)2=0,请计算休闲广场的面积.
20.数a在数轴上的位置如图,且|a+1|=2,求|3a+7|.
21.列式表示:
(1)比a的一半大3的数; (2)a与b的差的c倍; (3)a与b的倒数的和; (4)a与b的和的平方的相反数.
22.某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每个定价50元,厂方开展促销活动期间,可以同时向客户提供两种优惠方案:
方案一:买一台饮水机送一个饮水机桶;
方案二:饮水机和饮水机桶都按定价的九折付款.
现某客户到该饮水机厂购买饮水机20台,饮水机桶x(超过20)个.
(1)若该客户按方案一购买,求客户需付款钱数(用含x的式子表示);
若该客户按方案二购买,求客户需付款钱数(用含x的式子表示).
(2)若x=50,通过计算说明此时客户按哪种方案购买较合算.
(3)当x=50时,你还能给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出所需的钱数.
23.问题情境:如图,,定点E,F分别在直线,上,在平行线,之间有一个动点P,满足.求,,满足的数量关系.
思路点拨:由于点P是平行线,之间一动点,因此需对点P的位置进行分类讨论,过点P作的平行线,通过平行线的性质推出,,的数量关系.
(1)问题解决:如图1,当点P在的左侧时,写出,,满足的数量关系_____;如图2,当点P在的右侧时,写出,,满足的数量关系______.
(2)问题迁移:如图3,、分别平分和,且点P在左侧.
①若,则的度数为_______;
②猜想与的数量关系,并说明理由;
(3)问题拓展:如图4,若与的角平分线交于点,与的角平分线交于点,与的角平分线交于点,以此类推,直接写出与满足的数量关系.
参考答案及试题解析
1.C
2.C
3.B
【解答】解:∵9<11<16,
∴且3<<4,
∵a<<b,a、b是两个连续整数,
∴a=3,b=4,
∴a+b=3+4=7,
故选:B.
【分析】本题考查了无理数的大小估值,由9<11<16,得到3<<4,结合a、b是两个连续整数,求得a和b的值,将其代入代数式 a+b ,计算求值,即可得到答案.
4.B
5.D
【解答】解:∵p q= ,
∴y=2 x= 。
故答案为:D。
【分析】根据新定义运算的法则写出函数关系式,再根据所得函数的性质、图象与系数的关系即可得出答案。
6.C
【分析】首先将a-b=3、b+c=-5两式等号左右两边分别相加,得到a+c的值;再将代数式ac-bc+a2-ab分解因式转化为(a-b)(a+c);最后将a-b、a+c做为一个整体代入求得代数式的结果。
【解答】∵a-b=3,b+c=-5
∴a-b+b+c=3-5,解a+c=-2
∴ac-bc+a2-ab=c(a-b)+a(a-b)=(a-b)(a+c)=3×(-2)=-6
故选C
【点评】本题考查因式分解的应用、代数式求值.解决本题的关键是将a-b、b+c、a+c做为一个整体来应用。
7.A
【解答】∵2012÷2=1006∴2012是第1006个偶数,而1006÷4=251…2,
∴第1006个偶数在第252行,偶数行的数从第4列开始前面排,∴第1006个偶数在第3列,∴2012应在第252行第三列.
故答案为:A.
【分析】根据题意,找到规律即可作答。
8.C
【解答】由图可归纳出以下两条规律:(n为正整数)(1)第n次运动后,动点P的横坐标为n(2)在运动过程中,动点P的纵坐标是以 为循环变换的
则经过第27次运动后,动点 的横坐标为27
经过第27次运动后,动点 的纵坐标与第3次运动后,动点 的纵坐标相同,即为1
综上,所求的动点P的坐标是
故答案为:C.
【分析】根据图形中前几次运动后,动点P的坐标,归纳类推出规律,由此即可得出答案.
9.B
【解答】解:由图可知:
第一图:有花盆3个,每条边有2盆花,那么3=3×(2-1);
第二图:有花盆6个,每条边有3盆花,那么6=3×(3-1);
第三图:有花盆9个,每条边有4盆花,那么9=3×(4-1);
…
由此可知S与n的关系式为S=3(n-1).
故答案为:B.
【分析】根据题意找出规律得出S=3n-3,即可求解.
10.C
【解答】解:观察图形,得
图①用了5根火柴,即5=1×4+1,
图②用了9根火柴,即9=2×4+1,
图③用了13根火柴,即13=3×4+1,
…
图n用了(4n+1)根火柴,
根据题意得:4n+1=121,
解得n=30,
所以摆第,30个图案用121根火柴棒.
故答案为:C.
【分析】先找出规律求出图n用了(4n+1)根火柴,再求出4n+1=121,最后计算求解即可。
11.5
12.56
【解答】解:由图1得火柴根数
令则
由图2得火柴根数,
∴
∴正方形个数为:
故答案为:56.
【分析】由图1得火柴根数令求出火柴根数,根据图2得火柴根数,列方程即可求解.
13.1
【解答】解:∵一元二次方程的两个实数根分别是3、b
∴,解得:
∴
故答案为:1
【分析】根据二次方程中根与系数的关系列出方程组,解方程组可得a,b值,再代入代数式即可求出答案.
14.
15.
16.0
【解答】∵|x+y+z+1|=x+y+z+1或|x+y+z+1|=-(x+y+z+1),
∴x+y+z+1=x+y-z-2或-(x+y+z+1)=x+y-z-2,
∴z=- 或x+y= ,
当z=- 时,(x+y )(2z+3)=(x+y- )[2×(- )+3]=0;
当x+y= 时,(x+y )(2z+3)=( - )(2z+3)=0,
综上所述,(x+y )(2z+3)的值为0.
故答案为:0.
【分析】根据绝对值的意义可得|x+y+z+1|=x+y+z+1或|x+y+z+1|=-(x+y+z+1),从而可得x+y+z+1=x+y-z-2或-(x+y+z+1)=x+y-z-2,解得z=- 或x+y= ,然后将其分别代入原式中计算即可.
17.,4
18.解:∵ ,
∴x= y,z= y,
∴ =
【分析】由已知条件可得x=y,z=y,然后代入待求式中进行化简即可.
19.(1)解:由题意可得:
大长方形的面积为:(x+2y)(2x+y)m2
两正方形面积为:(2y2)m2
则休闲广场的面积为:
(x+2y)(2x+y)-2y2
=2x2+4xy+xy+2y2-2y2
=(2x2+5xy)m2
(2)解:由题意可得:
y-5=0,x-2=0
解得:y=5,x=2
则休闲广场的面积为:2×22+5×2×5=58m2
【分析】(1)根据休闲广场的面积=大长方形的面积-两小正方形的面积,列出代数式并化简即可求出答案.
(2)根据绝对值和偶次幂的非负性可求出x,y值,再代入(1)代数式即可求出答案.
20.解:∵|a+1|=2
∴a+1=2或-2
∴a=1或-3
当a=1时,|3a+7|=|3×1+7|=10
当a=-3时,|3a+7|=|3×(-3)+7|=2
【分析】 根据|a+1|=2, 结合绝对值的非负性求出a的值,然后分情况把a值代入 |3a+7| 求值即可.
21.(1 );(2)(a-b)c;(3)a+;(4)-(a+b)2
【解答】(1);(2)(a-b)c;(3)a+;(4)-(a+b)2
【分析】把问题中与数量有关的词语用含有数、字母和运算符号的式子表示出来就是列代数式;注意要弄清与运算有关词语的意义以及问题中“的”字处得运算的先后顺序.
22.(1)解:客户按方案一.购买需付款20×350+ (x-20) ×50=50x+20×(350-50)=(50x+6000)元;
客户按方案二购买需付款350×90%×20 + 50.×90%×x=(45x+6 300)元.
(2)解:当x=50时,
按方案一购买,需20×350+ (50- 20) ×50=8 500(元);
按方案二购买,需350×90%×20+ 50×90%×50=8 550(元).
所以按方案一购买合算.
(3)解:更为省钱的购买方案:按方案一购买20台饮水机,按方案二购买30个饮水机桶.
按方案一购买20台饮水机,送20个饮水机桶,需20×350=7 000(元),
按方案二购买30个饮水机桶,需50×90%×30=1350(元),
7 000+1 350=8 350(元),
故共需8 350元.
【分析】(1)按照对应的方案的计算方法分别列出代数式即可;
(2)把x = 50代入求得的代数式求得数值,进一步比较得出答案即可;
(3)根据两种方案的优惠方式,可得出先按方案一购买20台饮水机,送20只饮水机桶,另外30只饮水机桶再按方案二购买即可.
23.(1),.
(2)解:①
②如图3,,分别平分和,
设:,
,
则
,
,
即:.
(3)
【解答】(1)解:①当点P在的左侧时,
如图,过点P作,
,
,
,
,
;
②当点P在的右侧时,
如图,过点P作,
,
,
,
,
;
故答案为:;;
(2)解:①由(1)知,
,
,分别平分和,
,
,
,
,
,
故答案为;
(3)解:同理可得,
,
,
∴.
故答案为:.
【分析】(1)分类讨论:①当点P在的左侧时,②当点P在的右侧时,先分别画出图形并利用角的运算和等量代换求解即可;
(2)①利用角平分线的定义及角的运算和等量代换求出即可;
②先利用角平分线的定义及角的运算求出即可;
(3)先求出,,再求出即可.
(1)解:当点P在的左侧时,
如图,过点P作,
,
,
,
,
;
当点P在的右侧时,
如图,过点P作,
,
,
,
,
;
故答案为:,
;
(2)解:①由(1)知,
,
,分别平分和,
,
,
,
,
,
故答案为;
②如图3,,分别平分和,
设:,
,
则
,
,
即:;
(3)解:同理可得,
,
,
故:.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
