【章节考点培优】3.4二元一次方程组及其解法-2025-2026学年七年级上册数学沪科版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】3.4二元一次方程组及其解法-2025-2026学年七年级上册数学沪科版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 100.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 12:13:14 | ||
图片预览



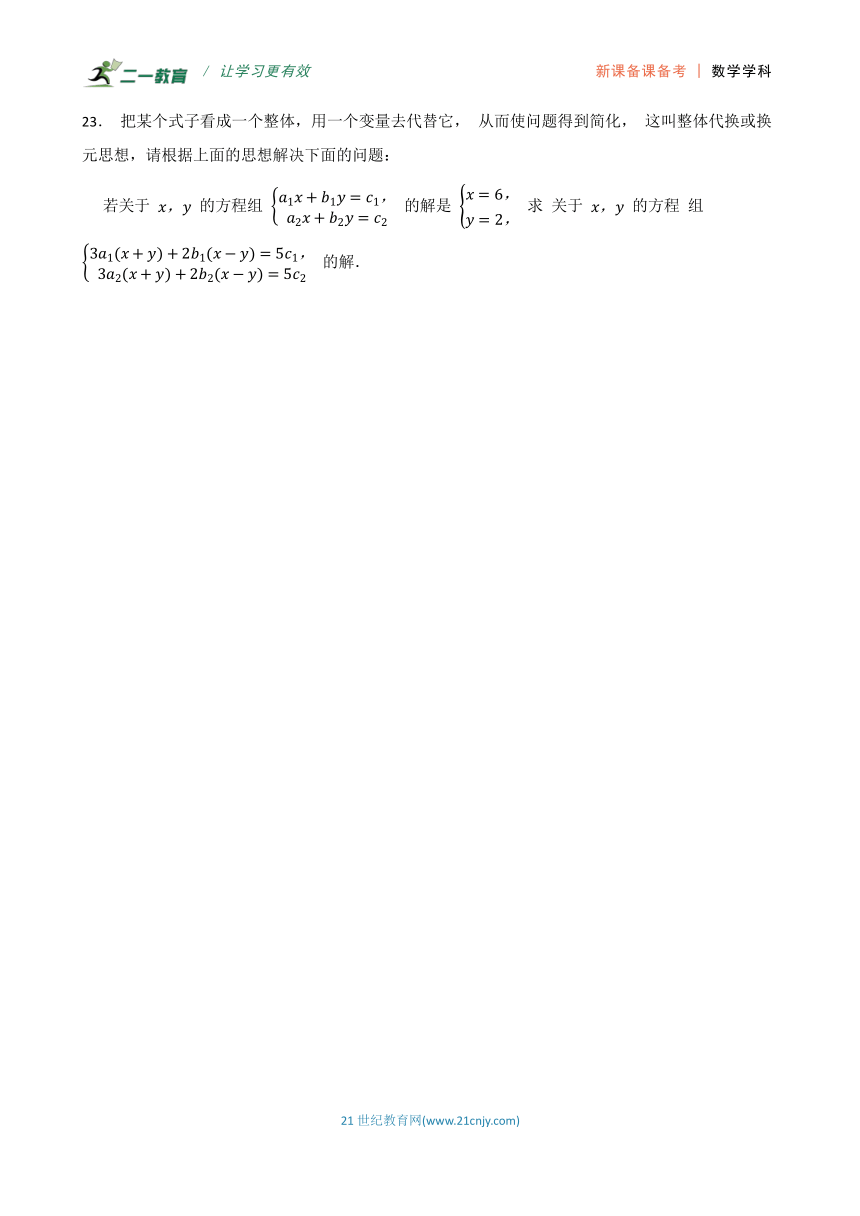

文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优沪科版(2024)
第3章 一次方程与方程组 3.4 二元一次方程组及其解法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在① +y=1;②3x-2y=1;③5xy=1;④ +y=1四个式子中,不是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
2.下列各方程组中,是二元一次方程组的是( )
A. B. C. D.
3.某公司上半年生产甲、乙两种型号的无人机若干架,已知甲种型号无人机架数比总架数的一半多 11 架,乙种型号无人机架数比总架数的三分之一少 2 架.设甲种型号无人机x 架,乙种型号无人机y 架,根据题意可列出的方程 组是( )
A. B.
C. D.
4.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是,求两种球各有多少个?若设篮球有x个,排球有y个,根据题意得方程组( )
A. B. C. D.
5.如果方程组 的解也是方程 的解,那么 的值是( )
A.1 B. C.-1 D.
6.已知是关于,的二元一次方程的一个解,则的值是( )
A.5 B.2 C. D.
7.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是( )
A. B. C. D.
8.四名学生解二元一次方程组提出四种不同的解法,其中解法不正确的是( )
A.由①得x=,代入② B.由①得y=,代入②
C.由②得y=,代入① D.由②得x=3+2y,代入①
9.已知是二元一次方程组的解,则的平方根为( )
A.2 B. C. D.
10.若甲数的3倍比乙数大7,设甲数为x,乙数为y,列出的二元一次方程为( )
A.3x+y=7 B.3x﹣y=7 C.3y﹣x=7 D.3y+x=7
二、填空题
11.已知方程,用含x的代数式表示y,即 .
12.关于 x,y 的方程组的解为,则①a2+ b2 ②关于 x,y 的方程组的解为 .
13.《孙子算经》中记载:“今有三人共车,二车空.二人共车,九人步.问人和车各几何 ”其大意是:今有若干人乘车,若每3人同乘一辆车,则最终剩余2辆空车;若每2人同乘一辆车,则最终剩下9人因无车可乘而步行,问有多少人,多少辆车 设有x辆车,y个人,则由题意可列方程组为 .
14.我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为 。
15.以为解的一个二元一次方程是
16.已知点 C、D是线段AB上两点(不与端点A、B重合),点A、B、C、D四点组成的所有线段的长度都是正整数,且总和为29,则线段AB的长度为 .
三、计算题
17.解方程组:
四、解答题
18.已知关于x、y的二元一次方程组 的解是 ,求关于a、b的二元一次方程组 的解.
19.七(1)班的56名学生决定利用节假日去镇江的五大景点当“小志愿者”,其中去“西津渡”景点的有27人,去“金山公园”的人数为x人,去“焦山”、“北固山”的人数都是y人,去“南山”的有6人.
(1)请列出关于x、y的等量关系式:______;
(2)若去“金山公园”的人数第二多,去南山的人数最少,求去“金山公园”的人数.
20.若关于 的二元一次方程组 的解满足 ,求出满足条件的 的所有正整数数值.
21.已知关于 的二元一次方程组
(1) 用含 的代数式表示 .
(2) 用含 的代数式表示方程组的解.
22.如图,已知二次函数经过A,B两点,轴于点C,且点,,.
(1)求抛物线的解析式;
(2)点E是线段上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段的长度最大时,求点E的坐标.
(3)点P是抛物线对称轴上的一个动点,是否存在这样的P点,使成为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
23. 把某个式子看成一个整体,用一个变量去代替它, 从而使问题得到简化, 这叫整体代换或换元思想,请根据上面的思想解决下面的问题:
若关于 的方程组 的解是 求 关于 的方程 组 的解.
参考答案及试题解析
1.B
【解答】由二元一次方程的定义可得:①、③共2个不是二元一次方程.
故答案为:B.
【分析】含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程,据此判断即可.
2.A
【解答】解:A:满足条件,符合题意;
B: 二元二次方程,不符合题意;
C: 是分式方程,不符合题意;
D:含有三个未知数,不符合题意.
故答案选:A.
【分析】二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程;二元一次方程组:两个二元一次方程结合在一起;根据定义判断即可.
3.B
4.D
5.A
【解答】解:解方程组 ,
解得: ,
把 代入 ,
得: ,
解得: ,
故答案为:A.
【分析】首先求出方程组的解,然后代入x+3y=12中就可求得k的值.
6.C
【解答】∵是关于x,y的二元一次方程x-2y=m的一个解,
∴1-2×3=m,
∴m=-5,
故答案为:C
【分析】将代入二元一次方程x-2y=m即可求m的值.
7.A
【解答】解:把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组 的解是 .
故答案为:A.
【分析】将x=1代入y=x+1即可求出y的值,进而得出.
8.C
【解答】解:A、正确,符合等式的性质;
B、正确,符合等式的性质;
C、错误,应该是由②得y=,代入①;
D、正确,符合等式的性质.
故选C.
【分析】此题中四位同学均利用了代入法求方程组的解,需对四个答案进行逐一分析求解.
9.B
【解答】解:将代入,
可得:,
解得:,
∴2m-n=2×3-2=4,
∴4的平方根是±2,
故答案为:B.
【分析】先将代入,求出m、n的值,再求出的值,最后利用平方根的计算方法分析求解即可.
10.B
【解答】解:根据甲数的3倍比乙数大7,得方程3x﹣y=7.
故选B.
【分析】此题中的等量关系为:甲数的3倍比乙数大7.
11.
12.;;.
【解答】①将代入方程组得:,
(1)+(2)得:,
∴;
②方程组整理得:,
仿照已知方程组得:,
解得:,
故答案为:;.
【分析】①把方程组的解代入方程求出a2和b2的值,然后整体代入解题;
②运用换元法解二元一次方程组即可.
13.
【解答】解:设有x辆车,y个人,
,
故答案为:.
【分析】设有x辆车,y个人,根据题干"若每3人同乘一辆车,则最终剩余2辆空车",据此列出第一个方程,然后再根据题干"若每2人同乘一辆车,则最终剩下9人因无车可乘",据此列出第二个方程将两个方程联立即可求解.
14.
【解答】解:∵花了100钱,
∴5×8+3x+y=100.
∵买了100只鸡,
∴8+x+y=100,
∴方程组为.
故答案为:.
【分析】根据花了100钱可得5×8+3x+y=100;根据买了100只鸡可得8+x+y=100,联立即可得到方程组.
15.x+y=12
【解答】解:例如1×5+1×7=12;将数字换为未知数,得x+y=12.答案不唯一.
【分析】利用方程的解构造一个等式,然后将数值换成未知数即可.
16.8或9
【解答】解:如图,图中共有线段6条,分别为AC、CD、DB,AD、BC、AB,
由题意得:AC+CD+DB+AD+BC+AB=29,
∵AC+CD+DB=AB,AD=AC+CD,BC=CD+DB,
∴3AB+CD=29,
又∵所有线段的长度都是正整数,AB>CD ,
∴AB=8,CD=5或AB=9,CD=2,
即AB的长度为8或9,
故答案为:8或9.
【分析】根据题意画出图形,可得图中共有线段6条,分别是AC、CD、DB,AD、BC、AB,然后根据所有线段的和为29可得3AB+CD=29,再根据所有线段的长度都是正整数,AB>CD,利用二元一次方程的解进行解答即可.
17.解:
由①+②,可得:
3x=6,
解得:x=2,
将x=2代入①,可得:
2+y=5,
解得:y=3,
∴方程组的解集为
【分析】利用加减消元法的计算方法及步骤分析求解即可.
18.解:∵关于x、y的二元一次方程组 的解是 ,
∴关于a.b的二元一次方程组 满足 ,
解得 .
故关于a.b的二元一次方程组 的解是 .
【分析】由题意可得关于a、b的方程组满足a+b=1,a-b=2,求出a、b的值即可.
19.(1)
(2)去“金山公园”的人数为9人
20.解:由
①+②得
由
满足条件的 的所有正整数数值是
【分析】将m当作常数,利用加减消元法求出x、y的值,再代入不等式求解即可。
21.(1)解:
用①+②得3x+y=7,
∴y=-3x+7;
(2)解:
①×2+②得5x=m+9,
解得,
用②×2-①得5y=8-3m,
解得
所以方程组的解为 .
【分析】(1)用①+②消去m可得关于字母x、y的二元一次方程,然后将含x的项及常数项放到方程的一边,未知数y的项放到方程的另一边即可;
(2)用①×2+②消去y可求出x的值,再用②×2-①消去x求出y的值,从而即可得出方程组的解.
22.(1)解:∵点,,
∴,,
∵,
∴,
把和代入二次函数中得:
,
解得:,
∴二次函数的解析式为:;
(2)解:如图1,∵直线经过点和,
设直线的解析式为,
∴,
解得:,
∴直线的解析式为:,
∵二次函数,
∴设点,则,
∴,
∴当时,的最大值为,
∴点E的坐标为;
(3)解:存在,∵,
∴对称轴为直线,
设,分三种情况:
①点B为直角顶点时,由勾股定理得:,
∴,
解得:,
∴;
②点A为直角顶点时,由勾股定理得:,
∴,
解得:,
∴;
③点P为直角顶点时,由勾股定理得:,
∴,
解得:或,
∴或;
综上,点P的坐标为或或或.
【分析】(1)先求得点B的坐标,然后将点A和点B的坐标代入抛物线的y=x2+bx+c可得到关于b、c的方程组,求解得b、c的值,从而即可得到抛物线的解析式;(2)先利用待定系数法求出直线AB的解析式,根据点的坐标与图形性质,设点E(t,t+1),则F(t,t2-2t-3),用两点间的距离公式表示出EF,利用配方法可求得EF的最大值以及点E的坐标;
(3)存在,设P(1,m),分三种情况:分别以A,B,P为直角顶点,根据勾股定理及两点间的距离公式分别列方程,解方程即可.
23.解:,
由题意知
解得
原方程组的解为
【分析】对原方程组进行变形可得根据关于 的方程组 的解是 可得 进而解得方程组的解为
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优沪科版(2024)
第3章 一次方程与方程组 3.4 二元一次方程组及其解法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在① +y=1;②3x-2y=1;③5xy=1;④ +y=1四个式子中,不是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4个
2.下列各方程组中,是二元一次方程组的是( )
A. B. C. D.
3.某公司上半年生产甲、乙两种型号的无人机若干架,已知甲种型号无人机架数比总架数的一半多 11 架,乙种型号无人机架数比总架数的三分之一少 2 架.设甲种型号无人机x 架,乙种型号无人机y 架,根据题意可列出的方程 组是( )
A. B.
C. D.
4.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是,求两种球各有多少个?若设篮球有x个,排球有y个,根据题意得方程组( )
A. B. C. D.
5.如果方程组 的解也是方程 的解,那么 的值是( )
A.1 B. C.-1 D.
6.已知是关于,的二元一次方程的一个解,则的值是( )
A.5 B.2 C. D.
7.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是( )
A. B. C. D.
8.四名学生解二元一次方程组提出四种不同的解法,其中解法不正确的是( )
A.由①得x=,代入② B.由①得y=,代入②
C.由②得y=,代入① D.由②得x=3+2y,代入①
9.已知是二元一次方程组的解,则的平方根为( )
A.2 B. C. D.
10.若甲数的3倍比乙数大7,设甲数为x,乙数为y,列出的二元一次方程为( )
A.3x+y=7 B.3x﹣y=7 C.3y﹣x=7 D.3y+x=7
二、填空题
11.已知方程,用含x的代数式表示y,即 .
12.关于 x,y 的方程组的解为,则①a2+ b2 ②关于 x,y 的方程组的解为 .
13.《孙子算经》中记载:“今有三人共车,二车空.二人共车,九人步.问人和车各几何 ”其大意是:今有若干人乘车,若每3人同乘一辆车,则最终剩余2辆空车;若每2人同乘一辆车,则最终剩下9人因无车可乘而步行,问有多少人,多少辆车 设有x辆车,y个人,则由题意可列方程组为 .
14.我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为 。
15.以为解的一个二元一次方程是
16.已知点 C、D是线段AB上两点(不与端点A、B重合),点A、B、C、D四点组成的所有线段的长度都是正整数,且总和为29,则线段AB的长度为 .
三、计算题
17.解方程组:
四、解答题
18.已知关于x、y的二元一次方程组 的解是 ,求关于a、b的二元一次方程组 的解.
19.七(1)班的56名学生决定利用节假日去镇江的五大景点当“小志愿者”,其中去“西津渡”景点的有27人,去“金山公园”的人数为x人,去“焦山”、“北固山”的人数都是y人,去“南山”的有6人.
(1)请列出关于x、y的等量关系式:______;
(2)若去“金山公园”的人数第二多,去南山的人数最少,求去“金山公园”的人数.
20.若关于 的二元一次方程组 的解满足 ,求出满足条件的 的所有正整数数值.
21.已知关于 的二元一次方程组
(1) 用含 的代数式表示 .
(2) 用含 的代数式表示方程组的解.
22.如图,已知二次函数经过A,B两点,轴于点C,且点,,.
(1)求抛物线的解析式;
(2)点E是线段上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段的长度最大时,求点E的坐标.
(3)点P是抛物线对称轴上的一个动点,是否存在这样的P点,使成为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
23. 把某个式子看成一个整体,用一个变量去代替它, 从而使问题得到简化, 这叫整体代换或换元思想,请根据上面的思想解决下面的问题:
若关于 的方程组 的解是 求 关于 的方程 组 的解.
参考答案及试题解析
1.B
【解答】由二元一次方程的定义可得:①、③共2个不是二元一次方程.
故答案为:B.
【分析】含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程,据此判断即可.
2.A
【解答】解:A:满足条件,符合题意;
B: 二元二次方程,不符合题意;
C: 是分式方程,不符合题意;
D:含有三个未知数,不符合题意.
故答案选:A.
【分析】二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程;二元一次方程组:两个二元一次方程结合在一起;根据定义判断即可.
3.B
4.D
5.A
【解答】解:解方程组 ,
解得: ,
把 代入 ,
得: ,
解得: ,
故答案为:A.
【分析】首先求出方程组的解,然后代入x+3y=12中就可求得k的值.
6.C
【解答】∵是关于x,y的二元一次方程x-2y=m的一个解,
∴1-2×3=m,
∴m=-5,
故答案为:C
【分析】将代入二元一次方程x-2y=m即可求m的值.
7.A
【解答】解:把x=1代入y=x+1,得出y=2,
函数y=x+1和y=ax+3的图象交于点P(1,2),
即x=1,y=2同时满足两个一次函数的解析式.
所以关于x,y的方程组 的解是 .
故答案为:A.
【分析】将x=1代入y=x+1即可求出y的值,进而得出.
8.C
【解答】解:A、正确,符合等式的性质;
B、正确,符合等式的性质;
C、错误,应该是由②得y=,代入①;
D、正确,符合等式的性质.
故选C.
【分析】此题中四位同学均利用了代入法求方程组的解,需对四个答案进行逐一分析求解.
9.B
【解答】解:将代入,
可得:,
解得:,
∴2m-n=2×3-2=4,
∴4的平方根是±2,
故答案为:B.
【分析】先将代入,求出m、n的值,再求出的值,最后利用平方根的计算方法分析求解即可.
10.B
【解答】解:根据甲数的3倍比乙数大7,得方程3x﹣y=7.
故选B.
【分析】此题中的等量关系为:甲数的3倍比乙数大7.
11.
12.;;.
【解答】①将代入方程组得:,
(1)+(2)得:,
∴;
②方程组整理得:,
仿照已知方程组得:,
解得:,
故答案为:;.
【分析】①把方程组的解代入方程求出a2和b2的值,然后整体代入解题;
②运用换元法解二元一次方程组即可.
13.
【解答】解:设有x辆车,y个人,
,
故答案为:.
【分析】设有x辆车,y个人,根据题干"若每3人同乘一辆车,则最终剩余2辆空车",据此列出第一个方程,然后再根据题干"若每2人同乘一辆车,则最终剩下9人因无车可乘",据此列出第二个方程将两个方程联立即可求解.
14.
【解答】解:∵花了100钱,
∴5×8+3x+y=100.
∵买了100只鸡,
∴8+x+y=100,
∴方程组为.
故答案为:.
【分析】根据花了100钱可得5×8+3x+y=100;根据买了100只鸡可得8+x+y=100,联立即可得到方程组.
15.x+y=12
【解答】解:例如1×5+1×7=12;将数字换为未知数,得x+y=12.答案不唯一.
【分析】利用方程的解构造一个等式,然后将数值换成未知数即可.
16.8或9
【解答】解:如图,图中共有线段6条,分别为AC、CD、DB,AD、BC、AB,
由题意得:AC+CD+DB+AD+BC+AB=29,
∵AC+CD+DB=AB,AD=AC+CD,BC=CD+DB,
∴3AB+CD=29,
又∵所有线段的长度都是正整数,AB>CD ,
∴AB=8,CD=5或AB=9,CD=2,
即AB的长度为8或9,
故答案为:8或9.
【分析】根据题意画出图形,可得图中共有线段6条,分别是AC、CD、DB,AD、BC、AB,然后根据所有线段的和为29可得3AB+CD=29,再根据所有线段的长度都是正整数,AB>CD,利用二元一次方程的解进行解答即可.
17.解:
由①+②,可得:
3x=6,
解得:x=2,
将x=2代入①,可得:
2+y=5,
解得:y=3,
∴方程组的解集为
【分析】利用加减消元法的计算方法及步骤分析求解即可.
18.解:∵关于x、y的二元一次方程组 的解是 ,
∴关于a.b的二元一次方程组 满足 ,
解得 .
故关于a.b的二元一次方程组 的解是 .
【分析】由题意可得关于a、b的方程组满足a+b=1,a-b=2,求出a、b的值即可.
19.(1)
(2)去“金山公园”的人数为9人
20.解:由
①+②得
由
满足条件的 的所有正整数数值是
【分析】将m当作常数,利用加减消元法求出x、y的值,再代入不等式求解即可。
21.(1)解:
用①+②得3x+y=7,
∴y=-3x+7;
(2)解:
①×2+②得5x=m+9,
解得,
用②×2-①得5y=8-3m,
解得
所以方程组的解为 .
【分析】(1)用①+②消去m可得关于字母x、y的二元一次方程,然后将含x的项及常数项放到方程的一边,未知数y的项放到方程的另一边即可;
(2)用①×2+②消去y可求出x的值,再用②×2-①消去x求出y的值,从而即可得出方程组的解.
22.(1)解:∵点,,
∴,,
∵,
∴,
把和代入二次函数中得:
,
解得:,
∴二次函数的解析式为:;
(2)解:如图1,∵直线经过点和,
设直线的解析式为,
∴,
解得:,
∴直线的解析式为:,
∵二次函数,
∴设点,则,
∴,
∴当时,的最大值为,
∴点E的坐标为;
(3)解:存在,∵,
∴对称轴为直线,
设,分三种情况:
①点B为直角顶点时,由勾股定理得:,
∴,
解得:,
∴;
②点A为直角顶点时,由勾股定理得:,
∴,
解得:,
∴;
③点P为直角顶点时,由勾股定理得:,
∴,
解得:或,
∴或;
综上,点P的坐标为或或或.
【分析】(1)先求得点B的坐标,然后将点A和点B的坐标代入抛物线的y=x2+bx+c可得到关于b、c的方程组,求解得b、c的值,从而即可得到抛物线的解析式;(2)先利用待定系数法求出直线AB的解析式,根据点的坐标与图形性质,设点E(t,t+1),则F(t,t2-2t-3),用两点间的距离公式表示出EF,利用配方法可求得EF的最大值以及点E的坐标;
(3)存在,设P(1,m),分三种情况:分别以A,B,P为直角顶点,根据勾股定理及两点间的距离公式分别列方程,解方程即可.
23.解:,
由题意知
解得
原方程组的解为
【分析】对原方程组进行变形可得根据关于 的方程组 的解是 可得 进而解得方程组的解为
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
