【章节考点培优】3.5二元一次方程组的应用-2025-2026学年七年级上册数学沪科版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】3.5二元一次方程组的应用-2025-2026学年七年级上册数学沪科版(2024)(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 211.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 00:00:00 | ||
图片预览



文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优沪科版(2024)
第3章 一次方程与方程组 3.5 二元一次方程组及其应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.我国民间流传着一道数学问题:只闻隔壁人分银,不知多少银和人:每人7两多7两,每人半斤少半斤(注;古代1斤=16两).试问各位善算者,多少人分多少银.设有人,分两银,根据题意列二元一次方程组正确的是( )
A. B.
C. D.
2.《孙子算经》中有一道题,原文是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”意思是:一个笼中装有鸡和兔子,上面数共有35个头,下面数共有九十四只脚,问鸡兔各有几只?如果设鸡有x只、兔有y只,则列出正确的方程组是( )
A. B.
C. D.
3.《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来记数、列式和进行演算的一种工具)来记录的.在算筹记数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式.如图(1),从左到右列出的算筹数分别表示、的系数与相应的常数项,根据图(1)可列出方程组,则根据图(2)列出的方程组是( )
A. B.
C. D.
4.阅读下列诗句:“栖树一群鸦,鸦树不知数,四只栖一树,两只没去处:六只栖一树,还闲一棵树,请你仔细数,鸦树各几何?”若设鸦有x只,树有y棵,则下列方程组中正确的是( )
A. B.
C. D.
5.如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
A. B.
C. D.
6.某年级学生共有246人,其中男生人数 比女生人数 的2倍少2人,则下面所列的方
程组中符合题意的有( )
A. B.
C. D.
7.《九章算术》中有这样一个题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意是:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有 辆车,人数为 ,根据题意,可列二元一次方程组为( )
A. B.
C. D.
8.古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )
A. B.
C. D.
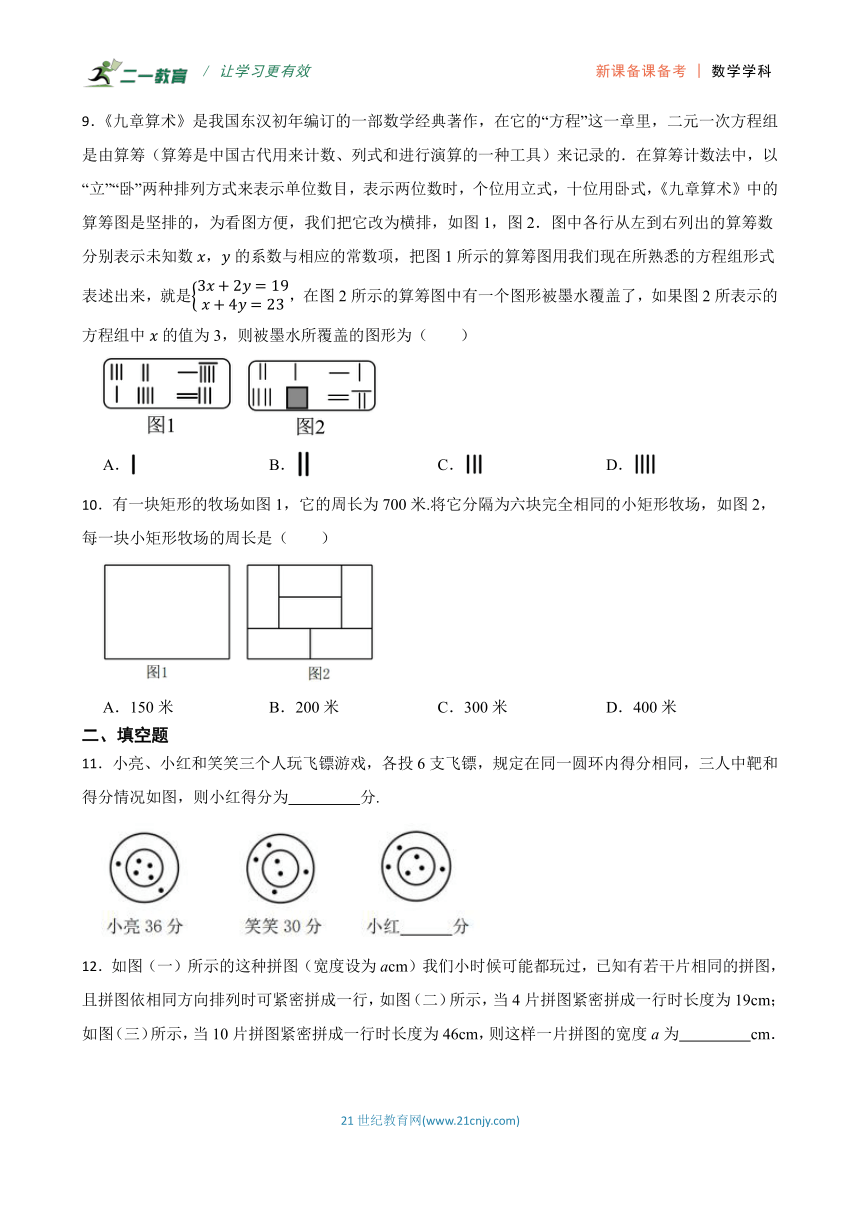
9.《九章算术》是我国东汉初年编订的一部数学经典著作,在它的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来计数、列式和进行演算的一种工具)来记录的.在算筹计数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式,《九章算术》中的算筹图是坚排的,为看图方便,我们把它改为横排,如图1,图2.图中各行从左到右列出的算筹数分别表示未知数,的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是,在图2所示的算筹图中有一个图形被墨水覆盖了,如果图2所表示的方程组中的值为3,则被墨水所覆盖的图形为( )
A. B. C. D.
10.有一块矩形的牧场如图1,它的周长为700米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是( )
A.150米 B.200米 C.300米 D.400米
二、填空题
11.小亮、小红和笑笑三个人玩飞镖游戏,各投6支飞镖,规定在同一圆环内得分相同,三人中靶和得分情况如图,则小红得分为 分.
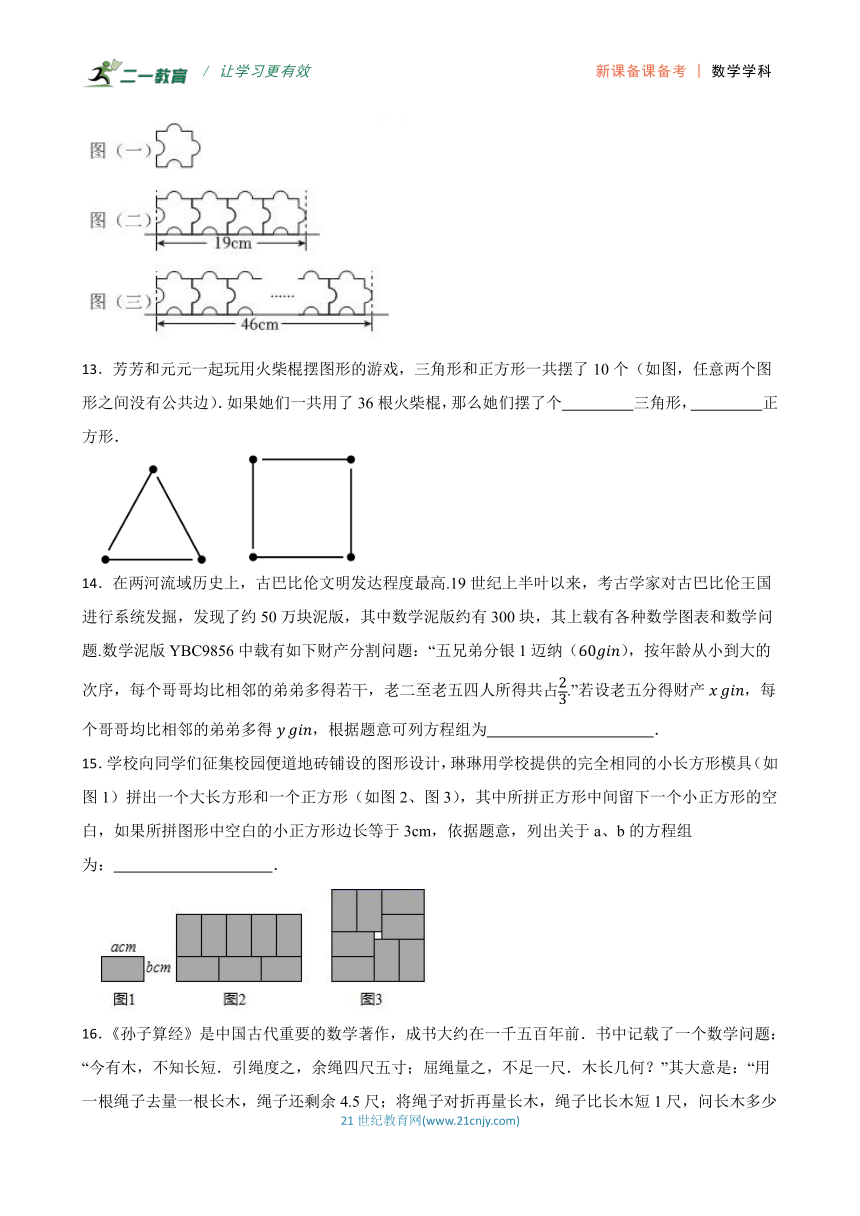
12.如图(一)所示的这种拼图(宽度设为acm)我们小时候可能都玩过,已知有若干片相同的拼图,且拼图依相同方向排列时可紧密拼成一行,如图(二)所示,当4片拼图紧密拼成一行时长度为19cm;如图(三)所示,当10片拼图紧密拼成一行时长度为46cm,则这样一片拼图的宽度a为 cm.
13.芳芳和元元一起玩用火柴棍摆图形的游戏,三角形和正方形一共摆了10个(如图,任意两个图形之间没有公共边).如果她们一共用了36根火柴棍,那么她们摆了个 三角形, 正方形.
14.在两河流域历史上,古巴比伦文明发达程度最高.19世纪上半叶以来,考古学家对古巴比伦王国进行系统发掘,发现了约50万块泥版,其中数学泥版约有300块,其上载有各种数学图表和数学问题.数学泥版YBC9856中载有如下财产分割问题:“五兄弟分银1迈纳(),按年龄从小到大的次序,每个哥哥均比相邻的弟弟多得若干,老二至老五四人所得共占.”若设老五分得财产,每个哥哥均比相邻的弟弟多得,根据题意可列方程组为 .
15.学校向同学们征集校园便道地砖铺设的图形设计,琳琳用学校提供的完全相同的小长方形模具(如图1)拼出一个大长方形和一个正方形(如图2、图3),其中所拼正方形中间留下一个小正方形的空白,如果所拼图形中空白的小正方形边长等于3cm,依据题意,列出关于a、b的方程组为: .
16.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.书中记载了一个数学问题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其大意是:“用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,绳子比长木短1尺,问长木多少尺?”设绳长尺,木长尺,可列方程组为 .
三、计算题
17.已知方程组 与方程组 有相同的解,求 、 的值.
四、解答题
18.夏季来临,天气逐渐炎热起来,某商店将某种碳酸饮料每瓶的价格上调了,将某种果汁饮料每瓶的价格下调了,已知调价前买这两种饮料各一瓶共花费15元,调价后买上述碳酸饮料1瓶和果汁饮料2瓶共花费24.5元,问这种碳酸饮料和果汁饮料在调价前每瓶各多少元?
19.端午节吃粽子是中华民族的传统习俗,根据调查发现,若购买豆沙粽盒、肉粽盒,共需元;若购买豆沙棕盒、肉粽盒,共需元.
(1)豆沙粽和肉粽的单价分别是多少元?
(2)某商家准备购进这两种粽子共盒,若商家最多能够提供元,则最多购进多少盒肉粽?
20.某厂生产甲、乙两种型号的产品,生产一个甲种产品需时间8s,铜8g;生产一个乙种产品需时间6s,铜16g.如果生产甲、乙两种产品共用时1h,共用铜6.4kg,那么甲、乙两种产品各生产多少个?
21.某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花3600元购买了黑白两种颜色的文化衫200件.每件文化衫的批发价及手绘后的零售价如下表:
批发价(元) 零售价(元)
黑色文化衫 20 35
白色文化衫 15 25
假设通过手绘设计后全部售出,求该校这次义卖活动所获利润.
22.国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,某公交公司积极响应将旧车换成节能环保公交车,已知购买A型和B型两种环保型公交车每辆的价格及每辆预计在某线路的年载客量如表:
A型 B型
价格(万元/台) x y
年载客量/万人次 60 100
若购买A型环保公交车2辆,B型环保公交车3辆,共需650万元;若购买A型环保公交车3辆,B型环保公交车2辆,共需600万元.
(1)求x、y的值;
(2)如果该公司计划购买A型和B型环保公交车共10辆,且总费用不超过1250万元,且确保这10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
23.4月9日上午8时,2017 徐州国际马拉松赛鸣枪开跑,一名 岁的男子带着他的两个孩子一同参加了比赛,下面是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
参考答案及试题解析
1.D
2.B
【解答】解:设鸡有x只,兔有y只,
根据题意,得,
故选:B.
【分析】设鸡有x只,兔有y只,根据题意建立方程组即可求出答案.
3.C
4.A
5.B
【解答】∵四边形ABCD和四边形EFGH是矩形,∴∠A=∠B=∠C=90°,∠AFE=∠FGB=∠CHG,EF=GH,∴△BGF∽△AFE,△AEF≌△CGH,又∵GF=2EF,AE=a,AF=b,∴BG=2b,BF=2a,CG=a,∵AB=4,BC=5,∴.故选:B.
【分析】由题意可知:△BGF∽△AFE,△AEF≌△CGH,再由GF=2EF,得出BG=2b,BF=2a,CG=a,由此根据AB=4,BC=5,列出方程组即可.
6.B
【解答】题目中的相等关系是①男生人数+女生人数=年级总人数,②男生人数比女生人数的2倍少2人则女生人数的2倍比男生人数多2,所以可以列出B.
【分析】列二元一次方程组的关键是找到题目中的相等关系.
7.A
【解答】解:设有 辆车,人数为
由“3人坐一辆车,则两辆车是空的”可得:
由“2人坐一辆车,则9人需要步行”可得:
即
故答案为A.
【分析】设有 辆车,人数为 ,根据“ 若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行 ”列出方程组即可.
8.D
9.C
10.C
【解答】解:设每一块小矩形牧场的长为x米,宽为y米,
解得
每一块小矩形牧场的周长是:100+100+50+50=300(米),
故答案为:C.
【分析】设每一块小矩形牧场的长为x米,宽为y米,根据图形可得x=2y;根据周长为700米可得3x+y=700÷2,联立可求出x、y的值,然后利用周长的意义进行解答.
11.33
【解答】解:设投中小圈得x分,投中大圈得y分,由题意得
,
得:,
∴小红得分为33分.
故答案为:33
【分析】设投中小圈得x分,投中大圈得y分,进而根据题意列出二元一次方程组,从而即可求解。
12.5.5
【解答】解:如图,设拼图的长度(x+y) cm
根据图二可知:3x+y=19
根据图三可知:10x+y=46
∴
解得:
∴a=x+y=5.5 cm
故答案为:5.5
【分析】把图一的拼图看成x+y的两个部分, 当4片拼图紧密拼成一行时长度为19cm 和 当10片拼图紧密拼成一行时长度为46cm ,即可以列出一个二元一次方程组,解出x和y的值,进而可以求出a的值.
13.4;6
14.
【解答】老五分得xgin,每个哥哥均比相邻的弟弟多得ygin,则老四分得(x+y)gin,老三分得(x+2y)gin,老二分得(x+3y)gin,老大分得(x+4y)gin,
根据题意则有:,
化简整理得:,
故答案为:.
【分析】老五分得xgin,每个哥哥均比相邻的弟弟多得ygin,则老四分得(x+y)gin,老三分得(x+2y)gin,老二分得(x+3y)gin,老大分得(x+4y)gin,根据:老二至老五四人所得共占 ,而老大共占,列出方程组即可.
15.
【解答】由分析知方程组为 .
故答案是: .
【分析】根据题意列出二元一次方程组求解即可。
16.
【解答】由题意:绳长比木长多4.5尺,绳长的一半比木长少1尺,可列出方程组 {x y=4.5y x2=1
故填: {x y=4.5y x2=1
【分析】根据已设未知数的逻辑关系,按照题意列方程组。
17.解:∵方程组 与方程组 有相同的解,
∴
解得
将 分别代入 ,得
解得
【分析】先将两个方程组中不含字母系数的方程组成新的方程组,从而求得x,y的值,再代入另两个含字母系数的方程中,从而组成关于字母系数m,n的方程组,解该方程组即可求得m,n的值.
18.解:设碳酸饮料和果汁饮料在调价前每瓶分别为元,元,由题意,得:
,
解得:;
答:碳酸饮料和果汁饮料在调价前每瓶分别为元和元.
【分析】本题考查二元一次方程组的实际应用,设碳酸饮料和果汁饮料在调价前每瓶分别为元,元,结合调价前买这两种饮料各一瓶共花费15元,调价后碳酸饮料1瓶和果汁饮料2瓶共花费24.5元,列出方程组,求得方程组的解,即可得到答案.
19.(1)解:设豆沙粽和肉粽的单价分别是元和元,
根据题意,有:,
解得:,
即豆沙粽和肉粽的单价分别是元和元
(2)解:设购买肉粽盒,则购买豆沙粽盒,
根据题意,有:,
解得:,
即最多购买肉粽盒.
【分析】(1)设豆沙粽和肉粽的单价分别是元和元,根据题意列出方程组,解方程组即可求出答案.
(2)设购买肉粽盒,则购买豆沙粽盒,根据题意列出不等式,解不等式即可求求出答案.
20.解:设甲产品x个,乙产品y个,根据题意,
得: ,
解得: .
答:生产甲产品240个,乙产品280个.
【分析】设甲产品x个、乙产品y个,根据甲产品时间+乙产品时间=3600秒,甲产品铜质量+乙产品铜质量=铜的总质量6400g,列方程组,解方程组可得.
21.该校这次义卖活动所获利润为2600元
22.(1)解:由题意,得,
解得;
(2)解:设购买A型环保公交车m辆,则购买B型环保公交车(10﹣m)辆,
由题意,得,
解得5≤m≤8,
∵m为整数,
∴有四种购车方案
方案一:购买A型公交车5辆,购买B型公交车5辆;
方案二:购买A型公交车6辆,购买B型公交车4辆;
方案三:购买A型公交车7辆,购买B型公交车3辆;
方案四:购买A型公交车8辆,购买B型公交车2辆.
(3)解:设购车总费用为w万元
则w=100m+150(10﹣m)=﹣50m+1500,
∵5≤m≤8且m为整数,
∴当m=5,6,7,8时,w分别1250,1200,1150,1100
∴m=8时,w最小=1100,
∴购车总费用最少的方案是购买A型公交车8辆,购买B型公交车2辆,购车总费用为1100万元.
【分析】(1)基本关系:金额=价格×数量,根据题意列二元一次方程组求解即可;
(2)设购买A型环保公交车m辆,则购买B型环保公交车(10-m)辆,根据题意列一元一次不等式组,即可求解;
(3)设购车总费用为w万元,根据总费用的数量关系建立w关于m的函数,再根据一次函数的性质求解即可.
23.解:设今年妹妹的年龄为x岁,哥哥的年龄为y岁,
根据题意得:
解得: .
答:今年妹妹6岁,哥哥10岁.
【分析】设今年妹妹的年龄为x岁,哥哥的年龄为y岁,根据题意可得等量关系式“妹妹的年龄+哥哥的年龄=16,3×(妹妹的年龄+2)+(哥哥的年龄+2)=34+2”,据此列方程组求解即可.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优沪科版(2024)
第3章 一次方程与方程组 3.5 二元一次方程组及其应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.我国民间流传着一道数学问题:只闻隔壁人分银,不知多少银和人:每人7两多7两,每人半斤少半斤(注;古代1斤=16两).试问各位善算者,多少人分多少银.设有人,分两银,根据题意列二元一次方程组正确的是( )
A. B.
C. D.
2.《孙子算经》中有一道题,原文是:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”意思是:一个笼中装有鸡和兔子,上面数共有35个头,下面数共有九十四只脚,问鸡兔各有几只?如果设鸡有x只、兔有y只,则列出正确的方程组是( )
A. B.
C. D.
3.《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来记数、列式和进行演算的一种工具)来记录的.在算筹记数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式.如图(1),从左到右列出的算筹数分别表示、的系数与相应的常数项,根据图(1)可列出方程组,则根据图(2)列出的方程组是( )
A. B.
C. D.
4.阅读下列诗句:“栖树一群鸦,鸦树不知数,四只栖一树,两只没去处:六只栖一树,还闲一棵树,请你仔细数,鸦树各几何?”若设鸦有x只,树有y棵,则下列方程组中正确的是( )
A. B.
C. D.
5.如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
A. B.
C. D.
6.某年级学生共有246人,其中男生人数 比女生人数 的2倍少2人,则下面所列的方
程组中符合题意的有( )
A. B.
C. D.
7.《九章算术》中有这样一个题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意是:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?设有 辆车,人数为 ,根据题意,可列二元一次方程组为( )
A. B.
C. D.
8.古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )
A. B.
C. D.
9.《九章算术》是我国东汉初年编订的一部数学经典著作,在它的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来计数、列式和进行演算的一种工具)来记录的.在算筹计数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式,《九章算术》中的算筹图是坚排的,为看图方便,我们把它改为横排,如图1,图2.图中各行从左到右列出的算筹数分别表示未知数,的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是,在图2所示的算筹图中有一个图形被墨水覆盖了,如果图2所表示的方程组中的值为3,则被墨水所覆盖的图形为( )
A. B. C. D.
10.有一块矩形的牧场如图1,它的周长为700米.将它分隔为六块完全相同的小矩形牧场,如图2,每一块小矩形牧场的周长是( )
A.150米 B.200米 C.300米 D.400米
二、填空题
11.小亮、小红和笑笑三个人玩飞镖游戏,各投6支飞镖,规定在同一圆环内得分相同,三人中靶和得分情况如图,则小红得分为 分.
12.如图(一)所示的这种拼图(宽度设为acm)我们小时候可能都玩过,已知有若干片相同的拼图,且拼图依相同方向排列时可紧密拼成一行,如图(二)所示,当4片拼图紧密拼成一行时长度为19cm;如图(三)所示,当10片拼图紧密拼成一行时长度为46cm,则这样一片拼图的宽度a为 cm.
13.芳芳和元元一起玩用火柴棍摆图形的游戏,三角形和正方形一共摆了10个(如图,任意两个图形之间没有公共边).如果她们一共用了36根火柴棍,那么她们摆了个 三角形, 正方形.
14.在两河流域历史上,古巴比伦文明发达程度最高.19世纪上半叶以来,考古学家对古巴比伦王国进行系统发掘,发现了约50万块泥版,其中数学泥版约有300块,其上载有各种数学图表和数学问题.数学泥版YBC9856中载有如下财产分割问题:“五兄弟分银1迈纳(),按年龄从小到大的次序,每个哥哥均比相邻的弟弟多得若干,老二至老五四人所得共占.”若设老五分得财产,每个哥哥均比相邻的弟弟多得,根据题意可列方程组为 .
15.学校向同学们征集校园便道地砖铺设的图形设计,琳琳用学校提供的完全相同的小长方形模具(如图1)拼出一个大长方形和一个正方形(如图2、图3),其中所拼正方形中间留下一个小正方形的空白,如果所拼图形中空白的小正方形边长等于3cm,依据题意,列出关于a、b的方程组为: .
16.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前.书中记载了一个数学问题:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其大意是:“用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,绳子比长木短1尺,问长木多少尺?”设绳长尺,木长尺,可列方程组为 .
三、计算题
17.已知方程组 与方程组 有相同的解,求 、 的值.
四、解答题
18.夏季来临,天气逐渐炎热起来,某商店将某种碳酸饮料每瓶的价格上调了,将某种果汁饮料每瓶的价格下调了,已知调价前买这两种饮料各一瓶共花费15元,调价后买上述碳酸饮料1瓶和果汁饮料2瓶共花费24.5元,问这种碳酸饮料和果汁饮料在调价前每瓶各多少元?
19.端午节吃粽子是中华民族的传统习俗,根据调查发现,若购买豆沙粽盒、肉粽盒,共需元;若购买豆沙棕盒、肉粽盒,共需元.
(1)豆沙粽和肉粽的单价分别是多少元?
(2)某商家准备购进这两种粽子共盒,若商家最多能够提供元,则最多购进多少盒肉粽?
20.某厂生产甲、乙两种型号的产品,生产一个甲种产品需时间8s,铜8g;生产一个乙种产品需时间6s,铜16g.如果生产甲、乙两种产品共用时1h,共用铜6.4kg,那么甲、乙两种产品各生产多少个?
21.某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花3600元购买了黑白两种颜色的文化衫200件.每件文化衫的批发价及手绘后的零售价如下表:
批发价(元) 零售价(元)
黑色文化衫 20 35
白色文化衫 15 25
假设通过手绘设计后全部售出,求该校这次义卖活动所获利润.
22.国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,某公交公司积极响应将旧车换成节能环保公交车,已知购买A型和B型两种环保型公交车每辆的价格及每辆预计在某线路的年载客量如表:
A型 B型
价格(万元/台) x y
年载客量/万人次 60 100
若购买A型环保公交车2辆,B型环保公交车3辆,共需650万元;若购买A型环保公交车3辆,B型环保公交车2辆,共需600万元.
(1)求x、y的值;
(2)如果该公司计划购买A型和B型环保公交车共10辆,且总费用不超过1250万元,且确保这10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
23.4月9日上午8时,2017 徐州国际马拉松赛鸣枪开跑,一名 岁的男子带着他的两个孩子一同参加了比赛,下面是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
参考答案及试题解析
1.D
2.B
【解答】解:设鸡有x只,兔有y只,
根据题意,得,
故选:B.
【分析】设鸡有x只,兔有y只,根据题意建立方程组即可求出答案.
3.C
4.A
5.B
【解答】∵四边形ABCD和四边形EFGH是矩形,∴∠A=∠B=∠C=90°,∠AFE=∠FGB=∠CHG,EF=GH,∴△BGF∽△AFE,△AEF≌△CGH,又∵GF=2EF,AE=a,AF=b,∴BG=2b,BF=2a,CG=a,∵AB=4,BC=5,∴.故选:B.
【分析】由题意可知:△BGF∽△AFE,△AEF≌△CGH,再由GF=2EF,得出BG=2b,BF=2a,CG=a,由此根据AB=4,BC=5,列出方程组即可.
6.B
【解答】题目中的相等关系是①男生人数+女生人数=年级总人数,②男生人数比女生人数的2倍少2人则女生人数的2倍比男生人数多2,所以可以列出B.
【分析】列二元一次方程组的关键是找到题目中的相等关系.
7.A
【解答】解:设有 辆车,人数为
由“3人坐一辆车,则两辆车是空的”可得:
由“2人坐一辆车,则9人需要步行”可得:
即
故答案为A.
【分析】设有 辆车,人数为 ,根据“ 若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行 ”列出方程组即可.
8.D
9.C
10.C
【解答】解:设每一块小矩形牧场的长为x米,宽为y米,
解得
每一块小矩形牧场的周长是:100+100+50+50=300(米),
故答案为:C.
【分析】设每一块小矩形牧场的长为x米,宽为y米,根据图形可得x=2y;根据周长为700米可得3x+y=700÷2,联立可求出x、y的值,然后利用周长的意义进行解答.
11.33
【解答】解:设投中小圈得x分,投中大圈得y分,由题意得
,
得:,
∴小红得分为33分.
故答案为:33
【分析】设投中小圈得x分,投中大圈得y分,进而根据题意列出二元一次方程组,从而即可求解。
12.5.5
【解答】解:如图,设拼图的长度(x+y) cm
根据图二可知:3x+y=19
根据图三可知:10x+y=46
∴
解得:
∴a=x+y=5.5 cm
故答案为:5.5
【分析】把图一的拼图看成x+y的两个部分, 当4片拼图紧密拼成一行时长度为19cm 和 当10片拼图紧密拼成一行时长度为46cm ,即可以列出一个二元一次方程组,解出x和y的值,进而可以求出a的值.
13.4;6
14.
【解答】老五分得xgin,每个哥哥均比相邻的弟弟多得ygin,则老四分得(x+y)gin,老三分得(x+2y)gin,老二分得(x+3y)gin,老大分得(x+4y)gin,
根据题意则有:,
化简整理得:,
故答案为:.
【分析】老五分得xgin,每个哥哥均比相邻的弟弟多得ygin,则老四分得(x+y)gin,老三分得(x+2y)gin,老二分得(x+3y)gin,老大分得(x+4y)gin,根据:老二至老五四人所得共占 ,而老大共占,列出方程组即可.
15.
【解答】由分析知方程组为 .
故答案是: .
【分析】根据题意列出二元一次方程组求解即可。
16.
【解答】由题意:绳长比木长多4.5尺,绳长的一半比木长少1尺,可列出方程组 {x y=4.5y x2=1
故填: {x y=4.5y x2=1
【分析】根据已设未知数的逻辑关系,按照题意列方程组。
17.解:∵方程组 与方程组 有相同的解,
∴
解得
将 分别代入 ,得
解得
【分析】先将两个方程组中不含字母系数的方程组成新的方程组,从而求得x,y的值,再代入另两个含字母系数的方程中,从而组成关于字母系数m,n的方程组,解该方程组即可求得m,n的值.
18.解:设碳酸饮料和果汁饮料在调价前每瓶分别为元,元,由题意,得:
,
解得:;
答:碳酸饮料和果汁饮料在调价前每瓶分别为元和元.
【分析】本题考查二元一次方程组的实际应用,设碳酸饮料和果汁饮料在调价前每瓶分别为元,元,结合调价前买这两种饮料各一瓶共花费15元,调价后碳酸饮料1瓶和果汁饮料2瓶共花费24.5元,列出方程组,求得方程组的解,即可得到答案.
19.(1)解:设豆沙粽和肉粽的单价分别是元和元,
根据题意,有:,
解得:,
即豆沙粽和肉粽的单价分别是元和元
(2)解:设购买肉粽盒,则购买豆沙粽盒,
根据题意,有:,
解得:,
即最多购买肉粽盒.
【分析】(1)设豆沙粽和肉粽的单价分别是元和元,根据题意列出方程组,解方程组即可求出答案.
(2)设购买肉粽盒,则购买豆沙粽盒,根据题意列出不等式,解不等式即可求求出答案.
20.解:设甲产品x个,乙产品y个,根据题意,
得: ,
解得: .
答:生产甲产品240个,乙产品280个.
【分析】设甲产品x个、乙产品y个,根据甲产品时间+乙产品时间=3600秒,甲产品铜质量+乙产品铜质量=铜的总质量6400g,列方程组,解方程组可得.
21.该校这次义卖活动所获利润为2600元
22.(1)解:由题意,得,
解得;
(2)解:设购买A型环保公交车m辆,则购买B型环保公交车(10﹣m)辆,
由题意,得,
解得5≤m≤8,
∵m为整数,
∴有四种购车方案
方案一:购买A型公交车5辆,购买B型公交车5辆;
方案二:购买A型公交车6辆,购买B型公交车4辆;
方案三:购买A型公交车7辆,购买B型公交车3辆;
方案四:购买A型公交车8辆,购买B型公交车2辆.
(3)解:设购车总费用为w万元
则w=100m+150(10﹣m)=﹣50m+1500,
∵5≤m≤8且m为整数,
∴当m=5,6,7,8时,w分别1250,1200,1150,1100
∴m=8时,w最小=1100,
∴购车总费用最少的方案是购买A型公交车8辆,购买B型公交车2辆,购车总费用为1100万元.
【分析】(1)基本关系:金额=价格×数量,根据题意列二元一次方程组求解即可;
(2)设购买A型环保公交车m辆,则购买B型环保公交车(10-m)辆,根据题意列一元一次不等式组,即可求解;
(3)设购车总费用为w万元,根据总费用的数量关系建立w关于m的函数,再根据一次函数的性质求解即可.
23.解:设今年妹妹的年龄为x岁,哥哥的年龄为y岁,
根据题意得:
解得: .
答:今年妹妹6岁,哥哥10岁.
【分析】设今年妹妹的年龄为x岁,哥哥的年龄为y岁,根据题意可得等量关系式“妹妹的年龄+哥哥的年龄=16,3×(妹妹的年龄+2)+(哥哥的年龄+2)=34+2”,据此列方程组求解即可.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
