初中数学人教版九年级上册 21.2.4 根与系数的关系 课件(13张PPT)
文档属性
| 名称 | 初中数学人教版九年级上册 21.2.4 根与系数的关系 课件(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 11:08:31 | ||
图片预览





文档简介
(共13张PPT)
第21章 一元二次方程
21.2.4
根与系数的关系
授课:
时间:
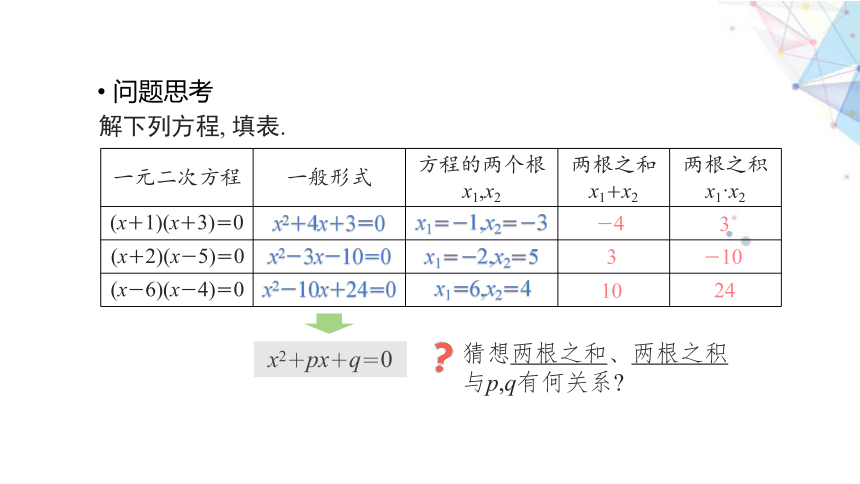
问题思考
一元二次方程 一般形式 方程的两个根 x1,x2 两根之和 x1+x2 两根之积
x1·x2
解下列方程, 填表.
(x+1)(x+3)=0
(x+2)(x-5)=0
(x-6)(x-4)=0
x2+4x+3=0
x2-3x-10=0
x2-10x+24=0
x1=-1,x2=-3
x1=-2,x2=5
x1=6,x2=4
-4
3
10
3
-10
24
x2+px+q=0
猜想两根之和、两根之积与p,q有何关系
验证猜想
猜想: 两根之和等于一次项系数的相反数,两根之积等于常数项.
已知: 关于x的一元二次方程x2+px+q=0的两个根为x1, x2.
求证: x1+x2=-p, x1·x2=q.
证明: ∵x1, x2是关于x的一元二次方程的两个根,
∴(x-x1)(x-x2)=0,
化为一般式为x-(x1+x2)x+x1·x2=0,
∴p= -(x1+x2), q= x1·x2,
即x1+x2=-p, x1·x2=q.
验证猜想
两根之和等于一次项系数的相反数,两根之积等于常数项.
如果关于x的一元二次方程x2+px+q=0的两个根为x1, x2,
那么x1+x2=-p, x1·x2=q.
使用结论时应注意什么?
①一元二次方程需要化为一般式, 且二次项系数为1;
②方程有两个根, 即△≥0.
典例精析
例1.求下列方程两根之和, 两根之积.
解: △=( 6)2 4×1×( 15)=96>0,
设方程的两个实数根为 1, 2,
则 1+ 2= ( 6)=6, 1· 2= 15.
(2) x2-4x+4=0.
解: △=(-4)2-4×4=0,
设方程的两个实数根为 1, 2,
则 1+ 2= ( 4)=4, 1· 2=4.
练习1.下列方程有实数根吗 若有, 求下列方程两根之和, 两根之积.
(2) -x2+6x-10=0.
(1) x2-6x-15=0;
(1) x2+2x-8=0;
解: △=22-4×(-8)=36>0,
设方程的两个实数根为 1, 2,
则 1+ 2= 2, 1· 2= 8.
解: △=62-4×(-1)×(-10) =-4<0,
∴该方程无实数根.
进一步思考
如果关于x的一元二次方程x2+px+q=0的两个根为x1, x2,
那么x1+x2=-p, x1·x2=q.
如果二次项系数不为1, 上述结论还成立吗
思考: 方程2x2-4x-10=0两根之和为_____, 两根之积为_____.
分析: 方程可化为x2-2x-5=0,
△=( 2)2 4×1×(-5)=24>0.
2
-5
进一步探索
一元二次方程 二次项系数化为1 两根之和x1+x2 两根之积x1·x2
3x2+6x-1=0
7x2-x-7=0
-5x2+4x+8=0
根据思考, 完成填表.
ax2+bx+c=0
我们如何计算它的两根之和, 两根之积
两根之和为 , 两根之积为 .
归纳总结
如果关于x的一元二次方程ax2+bx+c=0的两个根为x1, x2,
那么x1+x2= , x1·x2= .
(1) “韦达定理”使用的前提条件是什么?
一元二次方程根与系数的关系
①一元二次方程需要化为一般式;
②方程有两个根, 即△≥0.
(2) 你能用求根公式验证“韦达定理”吗?
典例精析
例2.已知m,n是方程3x2+4x-1=0的两个根.
(1)m+n=____,mn=____;
(2)求m2+n2的值.
解: 原式 .
练习2.方程ax2-x+1=0的有两个根x1,x2,其中x1=-1.
(1) 求a的值; (2) 求的值.
答案: (1) a=-2;(2)原式=1.
小试锋芒
练习3.若x2+px+q的两个实数根为-1,3,那么p=___,q=____.
-2
-3
练习4.若a、b是方程x2+x 2024=0的两个实数根, 则a2+2a+b的值是( ).
A. 2022 B. 2023 C. 2024 D. 2025
B
典例精析
例3.已知关于x的一元二次方程x2 x+2m 4=0有两个实数根.
(1)求m的取值范围;
(2)若方程的两根满足(x1 3)(x2 3)=m2 1, 求m的值.
解: 由题意得△=(-1)2-4×1×(2m-4)≥0,
解得m ≤ .
由题意得x1+x2=1,x1·x2=2m-4,
∴x1x2-3(x1+x2)+9=m2-1,
∴2m-4-3×1+9=m2-1,
即m2-2m-3=0,
解得m1=-1,m2=3(舍去).
小试锋芒
练习5.已知关于x的方程x2 2x+2k 1=0有实数根.
(1)求k的取值范围;
(2)设方程的两根分别是x1, x2, 且, 试求k的值.
答案: (1) k≤1;(2)k=-.
谢 谢 观 看
第21章 一元二次方程
21.2.4
根与系数的关系
授课:
时间:
问题思考
一元二次方程 一般形式 方程的两个根 x1,x2 两根之和 x1+x2 两根之积
x1·x2
解下列方程, 填表.
(x+1)(x+3)=0
(x+2)(x-5)=0
(x-6)(x-4)=0
x2+4x+3=0
x2-3x-10=0
x2-10x+24=0
x1=-1,x2=-3
x1=-2,x2=5
x1=6,x2=4
-4
3
10
3
-10
24
x2+px+q=0
猜想两根之和、两根之积与p,q有何关系
验证猜想
猜想: 两根之和等于一次项系数的相反数,两根之积等于常数项.
已知: 关于x的一元二次方程x2+px+q=0的两个根为x1, x2.
求证: x1+x2=-p, x1·x2=q.
证明: ∵x1, x2是关于x的一元二次方程的两个根,
∴(x-x1)(x-x2)=0,
化为一般式为x-(x1+x2)x+x1·x2=0,
∴p= -(x1+x2), q= x1·x2,
即x1+x2=-p, x1·x2=q.
验证猜想
两根之和等于一次项系数的相反数,两根之积等于常数项.
如果关于x的一元二次方程x2+px+q=0的两个根为x1, x2,
那么x1+x2=-p, x1·x2=q.
使用结论时应注意什么?
①一元二次方程需要化为一般式, 且二次项系数为1;
②方程有两个根, 即△≥0.
典例精析
例1.求下列方程两根之和, 两根之积.
解: △=( 6)2 4×1×( 15)=96>0,
设方程的两个实数根为 1, 2,
则 1+ 2= ( 6)=6, 1· 2= 15.
(2) x2-4x+4=0.
解: △=(-4)2-4×4=0,
设方程的两个实数根为 1, 2,
则 1+ 2= ( 4)=4, 1· 2=4.
练习1.下列方程有实数根吗 若有, 求下列方程两根之和, 两根之积.
(2) -x2+6x-10=0.
(1) x2-6x-15=0;
(1) x2+2x-8=0;
解: △=22-4×(-8)=36>0,
设方程的两个实数根为 1, 2,
则 1+ 2= 2, 1· 2= 8.
解: △=62-4×(-1)×(-10) =-4<0,
∴该方程无实数根.
进一步思考
如果关于x的一元二次方程x2+px+q=0的两个根为x1, x2,
那么x1+x2=-p, x1·x2=q.
如果二次项系数不为1, 上述结论还成立吗
思考: 方程2x2-4x-10=0两根之和为_____, 两根之积为_____.
分析: 方程可化为x2-2x-5=0,
△=( 2)2 4×1×(-5)=24>0.
2
-5
进一步探索
一元二次方程 二次项系数化为1 两根之和x1+x2 两根之积x1·x2
3x2+6x-1=0
7x2-x-7=0
-5x2+4x+8=0
根据思考, 完成填表.
ax2+bx+c=0
我们如何计算它的两根之和, 两根之积
两根之和为 , 两根之积为 .
归纳总结
如果关于x的一元二次方程ax2+bx+c=0的两个根为x1, x2,
那么x1+x2= , x1·x2= .
(1) “韦达定理”使用的前提条件是什么?
一元二次方程根与系数的关系
①一元二次方程需要化为一般式;
②方程有两个根, 即△≥0.
(2) 你能用求根公式验证“韦达定理”吗?
典例精析
例2.已知m,n是方程3x2+4x-1=0的两个根.
(1)m+n=____,mn=____;
(2)求m2+n2的值.
解: 原式 .
练习2.方程ax2-x+1=0的有两个根x1,x2,其中x1=-1.
(1) 求a的值; (2) 求的值.
答案: (1) a=-2;(2)原式=1.
小试锋芒
练习3.若x2+px+q的两个实数根为-1,3,那么p=___,q=____.
-2
-3
练习4.若a、b是方程x2+x 2024=0的两个实数根, 则a2+2a+b的值是( ).
A. 2022 B. 2023 C. 2024 D. 2025
B
典例精析
例3.已知关于x的一元二次方程x2 x+2m 4=0有两个实数根.
(1)求m的取值范围;
(2)若方程的两根满足(x1 3)(x2 3)=m2 1, 求m的值.
解: 由题意得△=(-1)2-4×1×(2m-4)≥0,
解得m ≤ .
由题意得x1+x2=1,x1·x2=2m-4,
∴x1x2-3(x1+x2)+9=m2-1,
∴2m-4-3×1+9=m2-1,
即m2-2m-3=0,
解得m1=-1,m2=3(舍去).
小试锋芒
练习5.已知关于x的方程x2 2x+2k 1=0有实数根.
(1)求k的取值范围;
(2)设方程的两根分别是x1, x2, 且, 试求k的值.
答案: (1) k≤1;(2)k=-.
谢 谢 观 看
同课章节目录
