人教版九年级数学上册23.1.1 图形的旋转课件(共17张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.1.1 图形的旋转课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 15:21:28 | ||
图片预览





文档简介
(共17张PPT)
第23章 旋转
23.1.1
图形的旋转
授课:
时间:
视频赏析
以上现象有什么特点
他们转动过程中, 其形状、大小、位置是否发生变化呢?
问题思考
钟表的指针在不停的转动,从1时到3时,时针是如何转动的
时针绕点O顺时针转动了60°.
O
A
A’
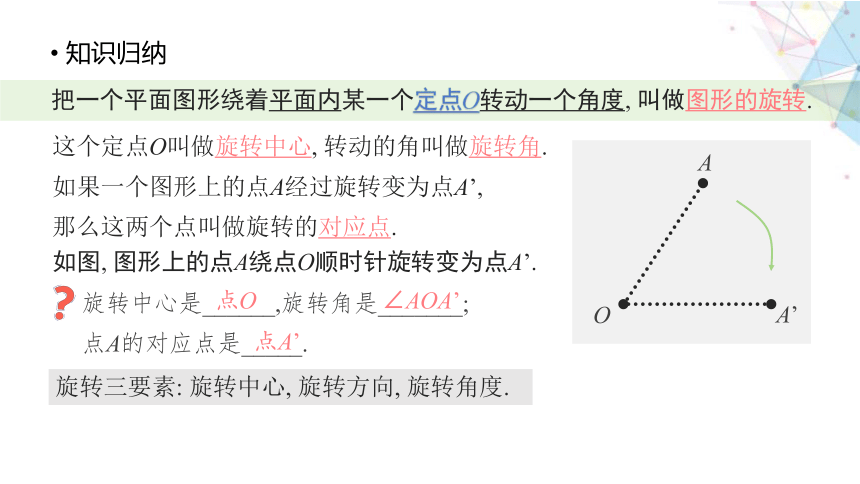
知识归纳
O
A
A’
把一个平面图形绕着平面内某一个定点O转动一个角度, 叫做图形的旋转.
这个定点O叫做旋转中心, 转动的角叫做旋转角.
如果一个图形上的点A经过旋转变为点A’,
那么这两个点叫做旋转的对应点.
如图, 图形上的点A绕点O顺时针旋转变为点A’.
旋转中心是______,旋转角是_______;
点A的对应点是_____.
点O
∠AOA’
点A’
旋转三要素: 旋转中心, 旋转方向, 旋转角度.
小试锋芒
练习1.下列属于旋转的是( ).
A. 足球在草地上向前滚动 B. 火箭升空的运动
C. 汽车在急刹车时向前滑行 D. 钟表的钟摆摆动的过程
D
练习2.将数字“6”旋转180°, 得到数字“9”, 将数字“9”旋转180°, 得到数字“6”, 现将数字“69”旋转180°, 得到的数字是( ).
A. 96 B. 69 C. 66 D. 99
B
小试锋芒
A
A’
B
B’
O
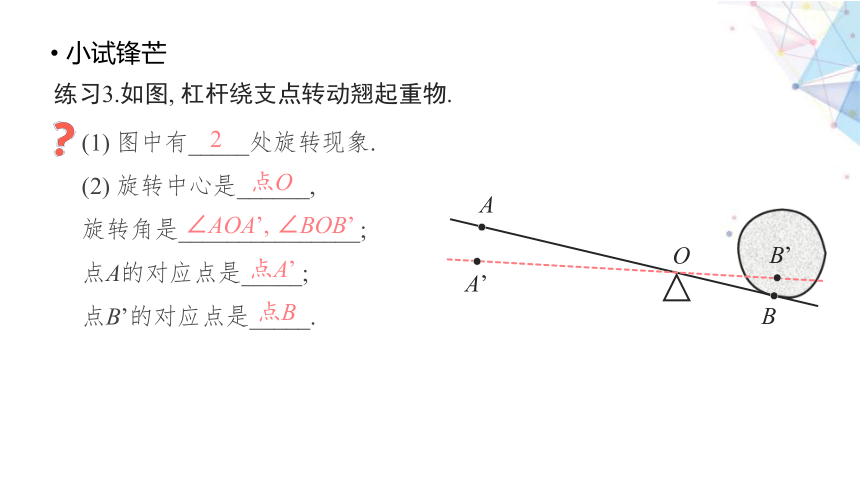
练习3.如图, 杠杆绕支点转动翘起重物.
(1) 图中有_____处旋转现象.
(2) 旋转中心是______,
旋转角是_______________;
点A的对应点是_____;
点B’的对应点是_____.
2
点O
∠AOA’, ∠BOB’
点A’
点B
进一步探索
O
问题探索
(1)旋转中心是______,旋转角是_______________________;
图中的对应点有哪些?
A
B
C
O
A’
B’
C’
点O
∠AOA’, ∠BOB’, ∠COC’
点A与点A’,点B与点B’,点C与点C’.
将△ABC绕点O顺时针旋转60°得到△A’B’C’.
(2) 连接OA,OA’,OB,OB’,OC,OC’,
对应点的连线有怎样的数量关系.
OA=OA’,OB=OB’,OC=OC’.
对应点到旋转中心的距离相等.
问题探索
A
B
C
O
A’
B’
C’
将△ABC绕点O顺时针旋转60°得到△A’B’C’.
(3)对应点与旋转中心所连线段的夹角有怎样的数量关系?
∠AOA’=∠BOB’=∠COC’.
对应点与旋转中心所连线段的夹角等于旋转角.
(4) △ABC与△A’B’C’的大小和形状相同吗
△ABC≌△A’B’C’
旋转前、后的图形全等.
归纳总结
A
B
C
O
A’
B’
C’
旋转的性质:
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
典例精析
例1.如图, 在Rt△ABC中, ∠C=90°, 将△ABC绕着点B顺时针旋转得到△FBE, 点C, 点A的对应点分别为点E, 点F, 点E落在BA上, 连接AF.
(1)若∠BAC=20°, 求∠BAF的度数;
证明: ∵∠C=90°, ∠BAC=20°, 由旋转可得
∴AB=BF,∠ABF=∠ABC=70°,
∴∠BAF=∠BFA==55°.
典例精析
例1.如图, 在Rt△ABC中, ∠C=90°, 将△ABC绕着点B顺时针旋转得到△FBE, 点C, 点A的对应点分别为点E, 点F, 点E落在BA上, 连接AF.
(2)若 AC=12, BC=5, 求AF的长.
解: 在Rt△ABC中, AB=,
由旋转可得AC=EF=12,BC=BE=5,
∴AE=8,
在Rt△AEF中, AF=.
小试锋芒
练习4.如图, 在△ABC中, ∠B=40°, 将△ABC绕点A逆时针旋转, 得到△ADE, 点D恰好落在BC的延长线上, 则旋转角的度数( ).
A. 70° B. 80° C. 90° D. 100°
D
练习5.如图, 在△ABC中, ∠ACB=90°, 将△ABC绕点C顺时针旋转得到△DEC, 使点B的对应点E恰好落在边AC上, 点A的对应点为D, 延长DE交AB于点F, 则下列结论一定正确的是( ).
A. AC=DE
B. BC=EF
C. ∠AEF=∠D
D. AB⊥DF
小试锋芒
D
小试锋芒
练习6.如图, 已知正方形ABCD的边长为3, E, F分别是AB, BC边上的点, 且∠EDF=45°, 将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证: EF=MF;
(2)当AE=1时, 求EF的长.
答案: (1) 证明△DEF≌△DMF即可;
(2) EF=2.5.
谢 谢 观 看
第23章 旋转
23.1.1
图形的旋转
授课:
时间:
视频赏析
以上现象有什么特点
他们转动过程中, 其形状、大小、位置是否发生变化呢?
问题思考
钟表的指针在不停的转动,从1时到3时,时针是如何转动的
时针绕点O顺时针转动了60°.
O
A
A’
知识归纳
O
A
A’
把一个平面图形绕着平面内某一个定点O转动一个角度, 叫做图形的旋转.
这个定点O叫做旋转中心, 转动的角叫做旋转角.
如果一个图形上的点A经过旋转变为点A’,
那么这两个点叫做旋转的对应点.
如图, 图形上的点A绕点O顺时针旋转变为点A’.
旋转中心是______,旋转角是_______;
点A的对应点是_____.
点O
∠AOA’
点A’
旋转三要素: 旋转中心, 旋转方向, 旋转角度.
小试锋芒
练习1.下列属于旋转的是( ).
A. 足球在草地上向前滚动 B. 火箭升空的运动
C. 汽车在急刹车时向前滑行 D. 钟表的钟摆摆动的过程
D
练习2.将数字“6”旋转180°, 得到数字“9”, 将数字“9”旋转180°, 得到数字“6”, 现将数字“69”旋转180°, 得到的数字是( ).
A. 96 B. 69 C. 66 D. 99
B
小试锋芒
A
A’
B
B’
O
练习3.如图, 杠杆绕支点转动翘起重物.
(1) 图中有_____处旋转现象.
(2) 旋转中心是______,
旋转角是_______________;
点A的对应点是_____;
点B’的对应点是_____.
2
点O
∠AOA’, ∠BOB’
点A’
点B
进一步探索
O
问题探索
(1)旋转中心是______,旋转角是_______________________;
图中的对应点有哪些?
A
B
C
O
A’
B’
C’
点O
∠AOA’, ∠BOB’, ∠COC’
点A与点A’,点B与点B’,点C与点C’.
将△ABC绕点O顺时针旋转60°得到△A’B’C’.
(2) 连接OA,OA’,OB,OB’,OC,OC’,
对应点的连线有怎样的数量关系.
OA=OA’,OB=OB’,OC=OC’.
对应点到旋转中心的距离相等.
问题探索
A
B
C
O
A’
B’
C’
将△ABC绕点O顺时针旋转60°得到△A’B’C’.
(3)对应点与旋转中心所连线段的夹角有怎样的数量关系?
∠AOA’=∠BOB’=∠COC’.
对应点与旋转中心所连线段的夹角等于旋转角.
(4) △ABC与△A’B’C’的大小和形状相同吗
△ABC≌△A’B’C’
旋转前、后的图形全等.
归纳总结
A
B
C
O
A’
B’
C’
旋转的性质:
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
典例精析
例1.如图, 在Rt△ABC中, ∠C=90°, 将△ABC绕着点B顺时针旋转得到△FBE, 点C, 点A的对应点分别为点E, 点F, 点E落在BA上, 连接AF.
(1)若∠BAC=20°, 求∠BAF的度数;
证明: ∵∠C=90°, ∠BAC=20°, 由旋转可得
∴AB=BF,∠ABF=∠ABC=70°,
∴∠BAF=∠BFA==55°.
典例精析
例1.如图, 在Rt△ABC中, ∠C=90°, 将△ABC绕着点B顺时针旋转得到△FBE, 点C, 点A的对应点分别为点E, 点F, 点E落在BA上, 连接AF.
(2)若 AC=12, BC=5, 求AF的长.
解: 在Rt△ABC中, AB=,
由旋转可得AC=EF=12,BC=BE=5,
∴AE=8,
在Rt△AEF中, AF=.
小试锋芒
练习4.如图, 在△ABC中, ∠B=40°, 将△ABC绕点A逆时针旋转, 得到△ADE, 点D恰好落在BC的延长线上, 则旋转角的度数( ).
A. 70° B. 80° C. 90° D. 100°
D
练习5.如图, 在△ABC中, ∠ACB=90°, 将△ABC绕点C顺时针旋转得到△DEC, 使点B的对应点E恰好落在边AC上, 点A的对应点为D, 延长DE交AB于点F, 则下列结论一定正确的是( ).
A. AC=DE
B. BC=EF
C. ∠AEF=∠D
D. AB⊥DF
小试锋芒
D
小试锋芒
练习6.如图, 已知正方形ABCD的边长为3, E, F分别是AB, BC边上的点, 且∠EDF=45°, 将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证: EF=MF;
(2)当AE=1时, 求EF的长.
答案: (1) 证明△DEF≌△DMF即可;
(2) EF=2.5.
谢 谢 观 看
同课章节目录
