人教版九年级数学上册23.1.2 旋转作图课件(共21张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.1.2 旋转作图课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 570.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 15:23:31 | ||
图片预览


文档简介
(共21张PPT)
第23章 旋转
23.1.2
旋转作图
授课:
时间:
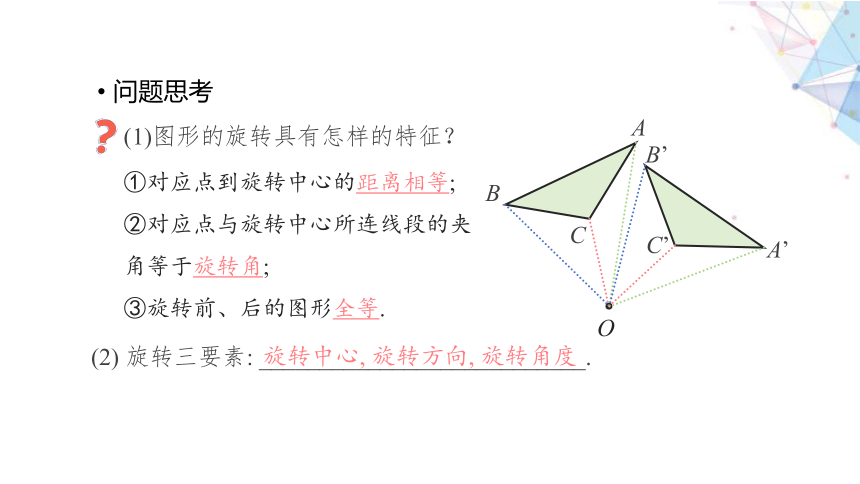
问题思考
A
B
C
O
A’
B’
C’
①对应点到旋转中心的距离相等;
②对应点与旋转中心所连线段的夹角等于旋转角;
③旋转前、后的图形全等.
(1)图形的旋转具有怎样的特征?
(2) 旋转三要素: ___________________________.
旋转中心, 旋转方向, 旋转角度
问题探索
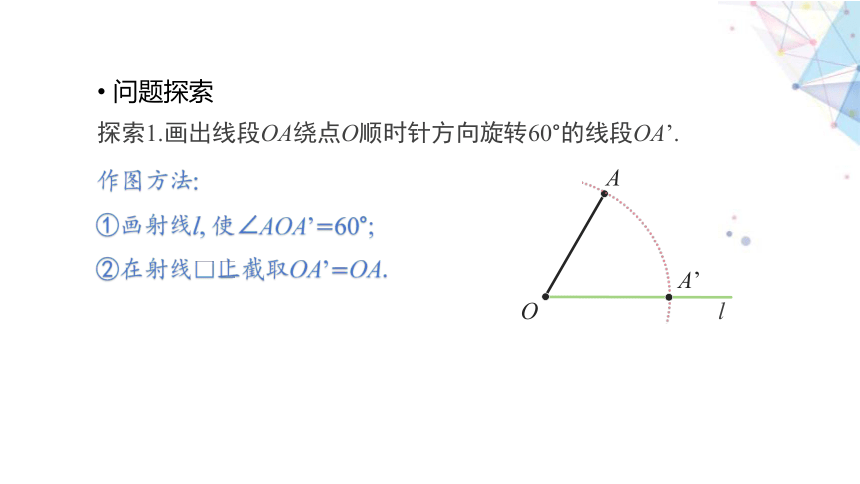
探索1.画出线段OA绕点O顺时针方向旋转60°的线段OA’.
O
A’
A
作图方法:
①画射线l, 使∠AOA’=60°;
②在射线 上截取OA’=OA.
l
问题探索
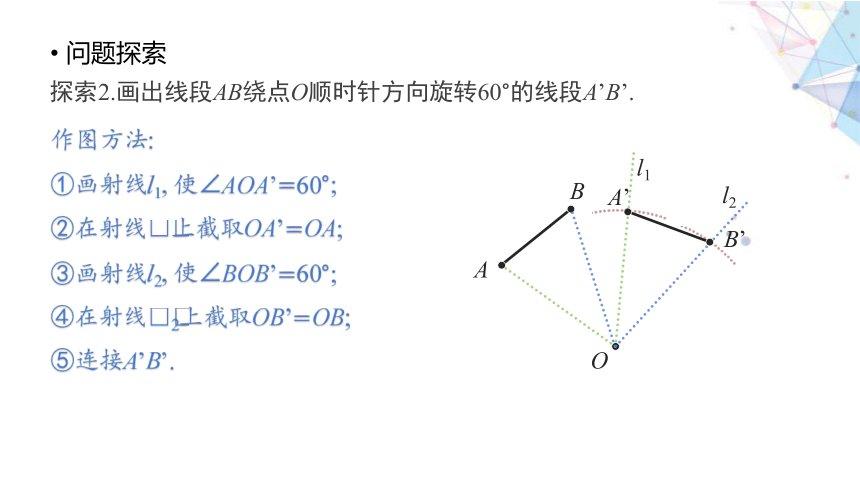
探索2.画出线段AB绕点O顺时针方向旋转60°的线段A’B’.
A
B
O
A’
B’
作图方法:
①画射线l1, 使∠AOA’=60°;
②在射线 上截取OA’=OA;
③画射线l2, 使∠BOB’=60°;
④在射线 2上截取OB’=OB;
⑤连接A’B’.
l1
l2
问题探索
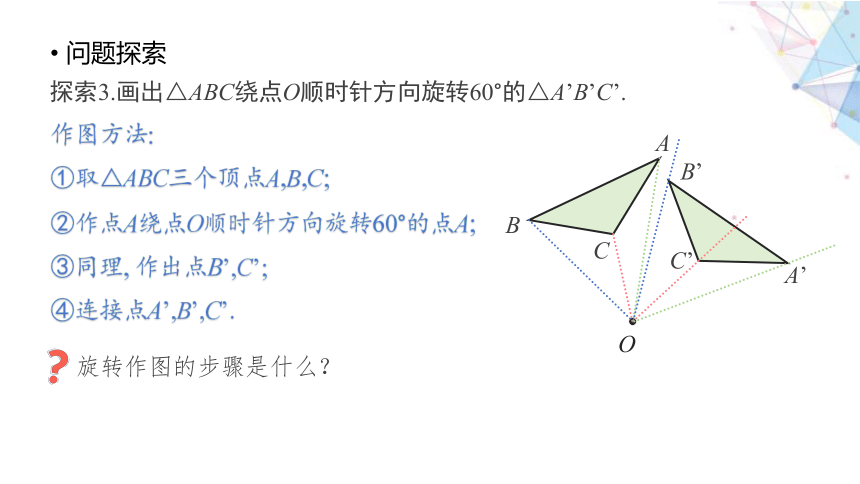
探索3.画出△ABC绕点O顺时针方向旋转60°的△A’B’C’.
O
A
B
C
A’
B’
C’
作图方法:
①取△ABC三个顶点A,B,C;
②作点A绕点O顺时针方向旋转60°的点A;
③同理, 作出点B’,C’;
④连接点A’,B’,C’.
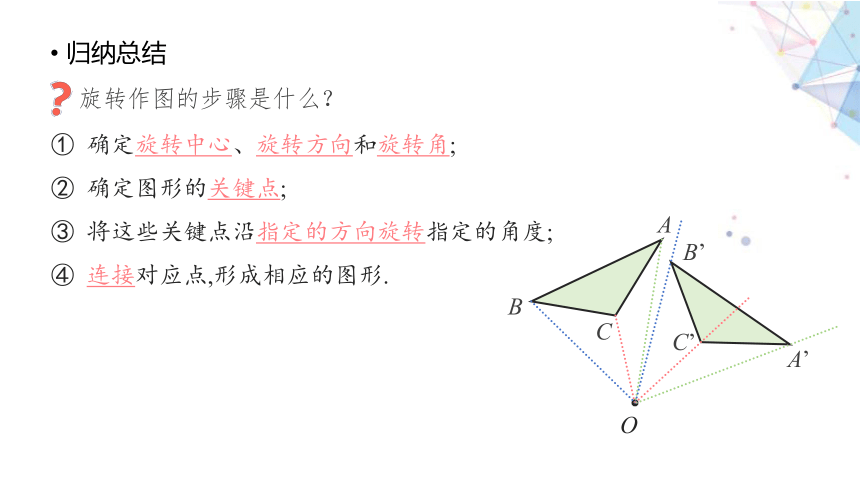
旋转作图的步骤是什么?
归纳总结
确定旋转中心、旋转方向和旋转角;
确定图形的关键点;
将这些关键点沿指定的方向旋转指定的角度;
④ 连接对应点,形成相应的图形.
旋转作图的步骤是什么?
O
A
B
C
A’
B’
C’
小组讨论
(1)图形的变换方式有哪些?
平移, 轴对称, 旋转.
(2)这些图形的变换方式有什么相同点和不同点
相同点: 都是全等变换, 即变换后的图形全等.
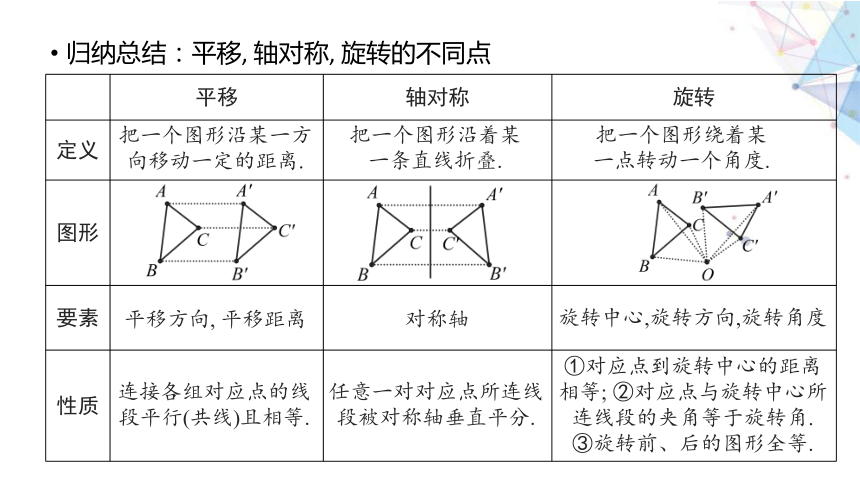
归纳总结:平移, 轴对称, 旋转的不同点
平移 轴对称 旋转
定义
图形
要素
性质
把一个图形沿某一方向移动一定的距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
平移方向, 平移距离
对称轴
旋转中心,旋转方向,旋转角度
连接各组对应点的线段平行(共线)且相等.
任意一对对应点所连线段被对称轴垂直平分.
①对应点到旋转中心的距离相等; ②对应点与旋转中心所连线段的夹角等于旋转角.
③旋转前、后的图形全等.
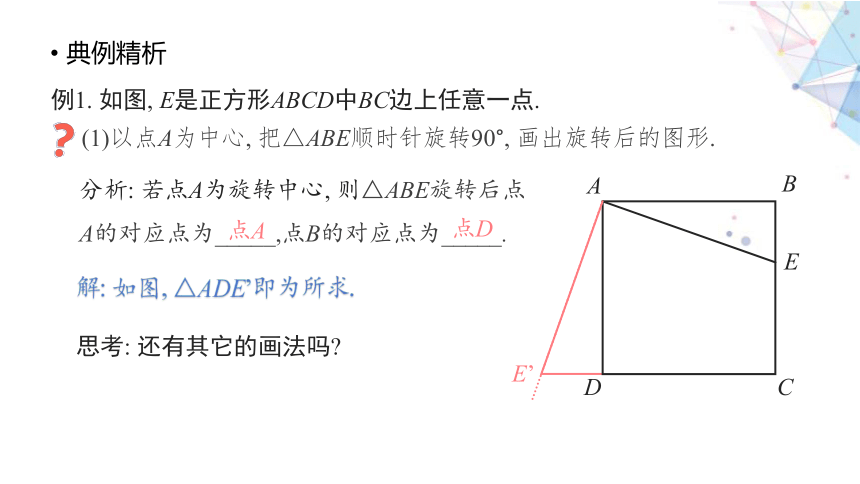
典例精析
例1. 如图, E是正方形ABCD中BC边上任意一点.
A
B
C
D
E
(1)以点A为中心, 把△ABE顺时针旋转90°, 画出旋转后的图形.
分析: 若点A为旋转中心, 则△ABE旋转后点A的对应点为_____,点B的对应点为_____.
点A
点D
E’
思考: 还有其它的画法吗
解: 如图, △ADE’即为所求.
典例精析
例1. 如图, E是正方形ABCD中BC边上任意一点.
A
B
C
D
E
(1)以点A为中心, 把△ABE顺时针旋转90°, 画出旋转后的图形.
分析:延长CD,在CD的延长线上截取DE’=BE,连接AE’.
E’
解: 如图, △ADE’即为所求.
(2)连接EE’,若AD=4,BE=3,求EE’的长.
典例精析
例1. 如图, E是正方形ABCD中BC边上任意一点.
A
B
C
D
E
E’
(2)连接EE’,若AD=4,BE=3,求EE’的长.
解: 在正方形ABCD中,AD=AB=4,
在Rt△ABE中, AE=,
由旋转可得AE’=AE=5,
∠EAE’=∠DAB=90°,
在Rt△EAE’中, EE’=.
小试锋芒
练习1.如图, P是等边△ABC内部任意一点.
作图: 将△ABP绕点B顺时针旋转60°得到△BCP’;
连接CP,PP’,若PA=6,PB=8,PC=10,求△CPP’的面积.
小试锋芒
解: (1) 如图△BCP’即为所求.
(2) △PCP’的面积为24.
练习1.如图, P是等边△ABC内部任意一点.
作图: 将△ABP绕点B顺时针旋转60°得到△BCP’;
连接CP,PP’,若PA=6,PB=8,PC=10,求△CPP’的面积.
典例精析
例2.如图, 线段AB绕一定点O顺时针旋转得到A’B’.
如何找到旋转中心O
分析:由旋转的性质可得,对应点到旋转中心的距离______,所以旋转中心在对应点连线的_____________.
相等
垂直平分线上
典例精析
例2.如图, 线段AB绕一定点O顺时针旋转得到A’B’.
如何找到旋转中心O
作图方法:
①连接AA’,作AA’的垂直平分线;
②连接BB’,作BB’的垂直平分线;
③两条垂直平分线的交点即旋转中心.
O
小试锋芒
练习2.如图, 在8×8的正方形网格中, △ABC绕某点旋转一定的角度, 得到△A′B′C′, 则旋转中心是_____.
点P
小试锋芒
练习3.如图, △ABC绕一定点O顺时针旋转得到△A’B’C’, 作旋转中心O.
解: 如图, 旋转中心O即为所求.
小试锋芒
练习4.(1)如图, △ABC关于l1对称的图形为________, △A’B’C’关于l2对称的图形为__________, 思考△A’’B’’C’’是由△ABC怎样得到的 你有什么发现
△A’’B’’C’’
△A’B’C’
结论: 图形经过两次轴对称(两对称轴相互平行)得到的图形,可以看作是由原图形经过平移得到的,也就是说两次翻折相当于一次平移.
解: 将△ABC向右平移可以得到△A’’B’’C’’.
小试锋芒
练习4.(2)如图, △ABC关于l1对称的图形为________, △A’B’C’关于l2对称的图形为__________, 思考△A’’B’’C’’是由△ABC怎样得到的 你有什么发现
△A’’B’’C’’
△A’B’C’
结论: 图形经过两次轴对称(两对称轴经过一定点)得到的图形,可以看作是由原图形绕该定点旋转得到的,也就是说两次翻折相当于一次旋转.
解: 将△ABC绕点O顺时针旋转可得到△A’’B’’C’’.
O
A
A
B
O
O
A
B
C
谢 谢 观 看
第23章 旋转
23.1.2
旋转作图
授课:
时间:
问题思考
A
B
C
O
A’
B’
C’
①对应点到旋转中心的距离相等;
②对应点与旋转中心所连线段的夹角等于旋转角;
③旋转前、后的图形全等.
(1)图形的旋转具有怎样的特征?
(2) 旋转三要素: ___________________________.
旋转中心, 旋转方向, 旋转角度
问题探索
探索1.画出线段OA绕点O顺时针方向旋转60°的线段OA’.
O
A’
A
作图方法:
①画射线l, 使∠AOA’=60°;
②在射线 上截取OA’=OA.
l
问题探索
探索2.画出线段AB绕点O顺时针方向旋转60°的线段A’B’.
A
B
O
A’
B’
作图方法:
①画射线l1, 使∠AOA’=60°;
②在射线 上截取OA’=OA;
③画射线l2, 使∠BOB’=60°;
④在射线 2上截取OB’=OB;
⑤连接A’B’.
l1
l2
问题探索
探索3.画出△ABC绕点O顺时针方向旋转60°的△A’B’C’.
O
A
B
C
A’
B’
C’
作图方法:
①取△ABC三个顶点A,B,C;
②作点A绕点O顺时针方向旋转60°的点A;
③同理, 作出点B’,C’;
④连接点A’,B’,C’.
旋转作图的步骤是什么?
归纳总结
确定旋转中心、旋转方向和旋转角;
确定图形的关键点;
将这些关键点沿指定的方向旋转指定的角度;
④ 连接对应点,形成相应的图形.
旋转作图的步骤是什么?
O
A
B
C
A’
B’
C’
小组讨论
(1)图形的变换方式有哪些?
平移, 轴对称, 旋转.
(2)这些图形的变换方式有什么相同点和不同点
相同点: 都是全等变换, 即变换后的图形全等.
归纳总结:平移, 轴对称, 旋转的不同点
平移 轴对称 旋转
定义
图形
要素
性质
把一个图形沿某一方向移动一定的距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
平移方向, 平移距离
对称轴
旋转中心,旋转方向,旋转角度
连接各组对应点的线段平行(共线)且相等.
任意一对对应点所连线段被对称轴垂直平分.
①对应点到旋转中心的距离相等; ②对应点与旋转中心所连线段的夹角等于旋转角.
③旋转前、后的图形全等.
典例精析
例1. 如图, E是正方形ABCD中BC边上任意一点.
A
B
C
D
E
(1)以点A为中心, 把△ABE顺时针旋转90°, 画出旋转后的图形.
分析: 若点A为旋转中心, 则△ABE旋转后点A的对应点为_____,点B的对应点为_____.
点A
点D
E’
思考: 还有其它的画法吗
解: 如图, △ADE’即为所求.
典例精析
例1. 如图, E是正方形ABCD中BC边上任意一点.
A
B
C
D
E
(1)以点A为中心, 把△ABE顺时针旋转90°, 画出旋转后的图形.
分析:延长CD,在CD的延长线上截取DE’=BE,连接AE’.
E’
解: 如图, △ADE’即为所求.
(2)连接EE’,若AD=4,BE=3,求EE’的长.
典例精析
例1. 如图, E是正方形ABCD中BC边上任意一点.
A
B
C
D
E
E’
(2)连接EE’,若AD=4,BE=3,求EE’的长.
解: 在正方形ABCD中,AD=AB=4,
在Rt△ABE中, AE=,
由旋转可得AE’=AE=5,
∠EAE’=∠DAB=90°,
在Rt△EAE’中, EE’=.
小试锋芒
练习1.如图, P是等边△ABC内部任意一点.
作图: 将△ABP绕点B顺时针旋转60°得到△BCP’;
连接CP,PP’,若PA=6,PB=8,PC=10,求△CPP’的面积.
小试锋芒
解: (1) 如图△BCP’即为所求.
(2) △PCP’的面积为24.
练习1.如图, P是等边△ABC内部任意一点.
作图: 将△ABP绕点B顺时针旋转60°得到△BCP’;
连接CP,PP’,若PA=6,PB=8,PC=10,求△CPP’的面积.
典例精析
例2.如图, 线段AB绕一定点O顺时针旋转得到A’B’.
如何找到旋转中心O
分析:由旋转的性质可得,对应点到旋转中心的距离______,所以旋转中心在对应点连线的_____________.
相等
垂直平分线上
典例精析
例2.如图, 线段AB绕一定点O顺时针旋转得到A’B’.
如何找到旋转中心O
作图方法:
①连接AA’,作AA’的垂直平分线;
②连接BB’,作BB’的垂直平分线;
③两条垂直平分线的交点即旋转中心.
O
小试锋芒
练习2.如图, 在8×8的正方形网格中, △ABC绕某点旋转一定的角度, 得到△A′B′C′, 则旋转中心是_____.
点P
小试锋芒
练习3.如图, △ABC绕一定点O顺时针旋转得到△A’B’C’, 作旋转中心O.
解: 如图, 旋转中心O即为所求.
小试锋芒
练习4.(1)如图, △ABC关于l1对称的图形为________, △A’B’C’关于l2对称的图形为__________, 思考△A’’B’’C’’是由△ABC怎样得到的 你有什么发现
△A’’B’’C’’
△A’B’C’
结论: 图形经过两次轴对称(两对称轴相互平行)得到的图形,可以看作是由原图形经过平移得到的,也就是说两次翻折相当于一次平移.
解: 将△ABC向右平移可以得到△A’’B’’C’’.
小试锋芒
练习4.(2)如图, △ABC关于l1对称的图形为________, △A’B’C’关于l2对称的图形为__________, 思考△A’’B’’C’’是由△ABC怎样得到的 你有什么发现
△A’’B’’C’’
△A’B’C’
结论: 图形经过两次轴对称(两对称轴经过一定点)得到的图形,可以看作是由原图形绕该定点旋转得到的,也就是说两次翻折相当于一次旋转.
解: 将△ABC绕点O顺时针旋转可得到△A’’B’’C’’.
O
A
A
B
O
O
A
B
C
谢 谢 观 看
同课章节目录
