23.2.2 中心对称图形 课件(共21张PPT) 人教版数学九年级上册
文档属性
| 名称 | 23.2.2 中心对称图形 课件(共21张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 11:55:19 | ||
图片预览





文档简介
(共21张PPT)
第23章 旋转
23.2.2
中心对称图形
授课:
时间:
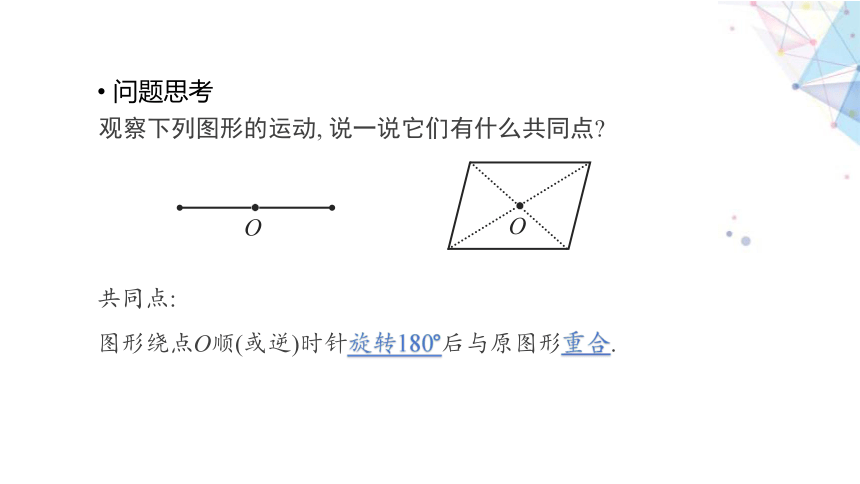
问题思考
观察下列图形的运动, 说一说它们有什么共同点
O
O
共同点:
图形绕点O顺(或逆)时针旋转180°后与原图形重合.
探索新知
把一个图形绕着某一个点旋转180°后, 如果旋转后的图形能和原来的图形重合, 那么这个图形叫做中心对称图形.
如图, □ABCD绕O旋转180°与原图形重合,
所以 □ABCD是中心对称图形.
点O为对称中心 (或中心),
旋转前后的点A与点C, 点B与点D能够重合,
所以点A与点C, 点B与点D是对称点(或对应点).
O
A
B
C
D
小试锋芒
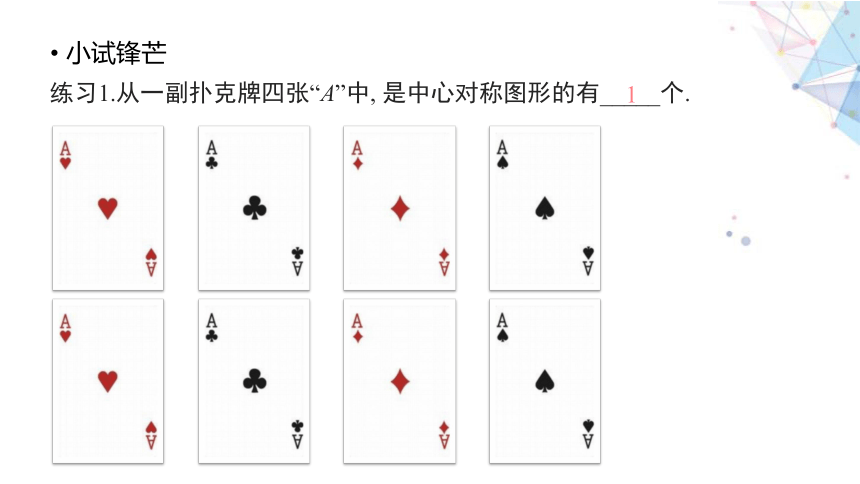
练习1.从一副扑克牌四张“A”中, 是中心对称图形的有_____个.
1
小试锋芒
练习2.下列四个“标识”中, 是中心对称图形是______.
①禁止通行
②注意安全
③有电危险
④预防溺水
①③
小试锋芒
练习2.下列四个“标识”中, 是中心对称图形是______.
①禁止通行
②注意安全
③有电危险
④预防溺水
①③
图中是轴对称图形的是_______.
①②④
典例精析
例1.在3×3的方格中, 有3个小方格涂上阴影, 请选择1个格子涂上阴影, 使其满足以下条件:
(1)使阴影部分变成轴对称图形 ;
①
②
③
④
⑤
(2)使阴影部分变成中心对称图形;
(3)使阴影部分既是中心对称图形,也是轴对称图形.
⑥
可涂上阴影的格子: ②,③,④,⑤.
可涂上阴影的格子: ①,⑤,⑥.
可涂上阴影的格子: ⑤.
小试锋芒
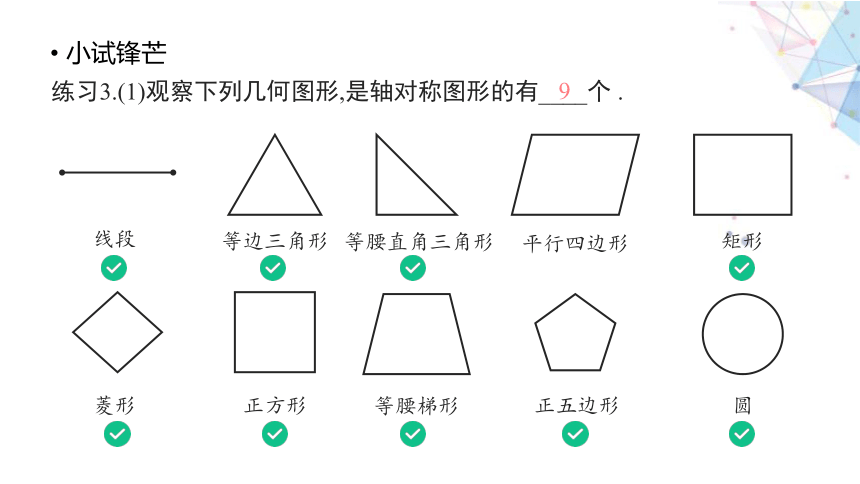
练习3.(1)观察下列几何图形,是轴对称图形的有____个 .
线段
等边三角形
等腰直角三角形
平行四边形
矩形
菱形
正方形
等腰梯形
正五边形
圆
9
小试锋芒
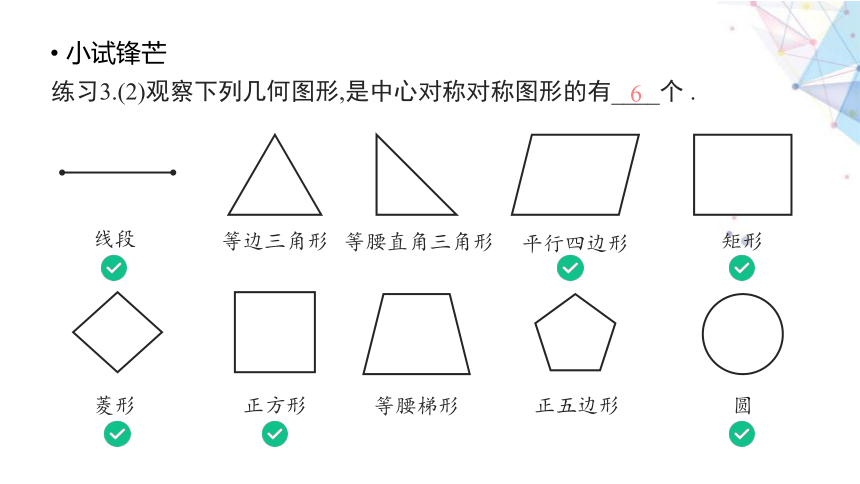
练习3.(2)观察下列几何图形,是中心对称对称图形的有____个 .
线段
等边三角形
等腰直角三角形
平行四边形
矩形
菱形
正方形
等腰梯形
正五边形
圆
6
小试锋芒
练习3.(3)下列几何图形,既是轴对称图形, 也是中心对称对称图形的有___个 .
线段
等边三角形
等腰直角三角形
平行四边形
矩形
菱形
正方形
等腰梯形
正五边形
圆
5
问题探索
O
A
B
C
D
如图, □ABCD是中心对称图形, 点O是对称中心.
图中OA,OB,OC,OD有怎样的数量关系
OA=OC,OB=OD
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
中心对称图形的性质:
探索新知
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
O
A
B
C
D
E
F
如图, □ABCD是中心对称图形, 点O是对称中心.
(1)你能得出OE, OF有怎样的数量关系吗
证明:∵□ABCD是中心对称图形,
点E,F是关于点O的对称点,
∴OE=OF.
(2)猜想图中四边形AEFB和四边形EDCF的面积有什么数量关系
四边形AEFB和四边形EDCF的面积相等.
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
归纳总结
O
A
B
C
D
E
F
常见的中心对称图形:
线段,矩形,菱形,正方形,平行四边形,圆.
中心对称图形的性质:
1.中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
2.过对称中心的直线可以把中心对称图形分成面积相等的两部分.
小智的问题
小智:我有一个“L”形的图形,我想把它的面积均分成两部分.
A
B
C
D
E
F
l
G
作图方法:
①延长DE交AB于点G,将图形分成矩形AGEF和矩形GBCD;
②作矩形AGEF和矩形GBCD的对称中心O1,O2;
③过O1, O2的直线l即为所求.
O1
O2
还有其它的方法吗?
小试锋芒
练习4.如图, 直线EF经过平行四边形ABCD的对角线的一交点O, 若AE=2cm, 四边形AEFB的面积为12cm2, 则CF=____, 平行四边形ABCD的面积为_____.
O
A
B
C
D
E
F
2cm
24cm2
问题思考
中心对称图形
轴对称图形
中心对称
(1) 中心对称图形和轴对称图形有什么区别?
(2) 中心对称图形和中心对称有什么区别与联系?
归纳总结
中心对称图形和轴对称图形有什么区别?
中心对称图形 轴对称图形
图形
不同点
有一个对称中心(点),
旋转前后图形全等
(对应线段、对应角相等),
旋转中心平分对应点所连线段.
有一条对称轴(直线),
对折前后图形全等
(对应线段、对应角相等)
对称轴垂直平分对应点所连线段.
归纳总结
中心对称图形和中心对称有什么区别与联系?
中心对称图形 中心对称
图形
相同点
不同点
研究对象是1个图形
研究对象是2个图形
变化形式都是图形绕对称中心旋转180°;
旋转后与原图重合(性质相同).
感悟生活
在生活中, 有许多根据中心对称图形设计出非常美丽的图案.
感悟生活
在生活中, 也有许多根据中心对称图形.
谢 谢 观 看
第23章 旋转
23.2.2
中心对称图形
授课:
时间:
问题思考
观察下列图形的运动, 说一说它们有什么共同点
O
O
共同点:
图形绕点O顺(或逆)时针旋转180°后与原图形重合.
探索新知
把一个图形绕着某一个点旋转180°后, 如果旋转后的图形能和原来的图形重合, 那么这个图形叫做中心对称图形.
如图, □ABCD绕O旋转180°与原图形重合,
所以 □ABCD是中心对称图形.
点O为对称中心 (或中心),
旋转前后的点A与点C, 点B与点D能够重合,
所以点A与点C, 点B与点D是对称点(或对应点).
O
A
B
C
D
小试锋芒
练习1.从一副扑克牌四张“A”中, 是中心对称图形的有_____个.
1
小试锋芒
练习2.下列四个“标识”中, 是中心对称图形是______.
①禁止通行
②注意安全
③有电危险
④预防溺水
①③
小试锋芒
练习2.下列四个“标识”中, 是中心对称图形是______.
①禁止通行
②注意安全
③有电危险
④预防溺水
①③
图中是轴对称图形的是_______.
①②④
典例精析
例1.在3×3的方格中, 有3个小方格涂上阴影, 请选择1个格子涂上阴影, 使其满足以下条件:
(1)使阴影部分变成轴对称图形 ;
①
②
③
④
⑤
(2)使阴影部分变成中心对称图形;
(3)使阴影部分既是中心对称图形,也是轴对称图形.
⑥
可涂上阴影的格子: ②,③,④,⑤.
可涂上阴影的格子: ①,⑤,⑥.
可涂上阴影的格子: ⑤.
小试锋芒
练习3.(1)观察下列几何图形,是轴对称图形的有____个 .
线段
等边三角形
等腰直角三角形
平行四边形
矩形
菱形
正方形
等腰梯形
正五边形
圆
9
小试锋芒
练习3.(2)观察下列几何图形,是中心对称对称图形的有____个 .
线段
等边三角形
等腰直角三角形
平行四边形
矩形
菱形
正方形
等腰梯形
正五边形
圆
6
小试锋芒
练习3.(3)下列几何图形,既是轴对称图形, 也是中心对称对称图形的有___个 .
线段
等边三角形
等腰直角三角形
平行四边形
矩形
菱形
正方形
等腰梯形
正五边形
圆
5
问题探索
O
A
B
C
D
如图, □ABCD是中心对称图形, 点O是对称中心.
图中OA,OB,OC,OD有怎样的数量关系
OA=OC,OB=OD
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
中心对称图形的性质:
探索新知
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
O
A
B
C
D
E
F
如图, □ABCD是中心对称图形, 点O是对称中心.
(1)你能得出OE, OF有怎样的数量关系吗
证明:∵□ABCD是中心对称图形,
点E,F是关于点O的对称点,
∴OE=OF.
(2)猜想图中四边形AEFB和四边形EDCF的面积有什么数量关系
四边形AEFB和四边形EDCF的面积相等.
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
归纳总结
O
A
B
C
D
E
F
常见的中心对称图形:
线段,矩形,菱形,正方形,平行四边形,圆.
中心对称图形的性质:
1.中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
2.过对称中心的直线可以把中心对称图形分成面积相等的两部分.
小智的问题
小智:我有一个“L”形的图形,我想把它的面积均分成两部分.
A
B
C
D
E
F
l
G
作图方法:
①延长DE交AB于点G,将图形分成矩形AGEF和矩形GBCD;
②作矩形AGEF和矩形GBCD的对称中心O1,O2;
③过O1, O2的直线l即为所求.
O1
O2
还有其它的方法吗?
小试锋芒
练习4.如图, 直线EF经过平行四边形ABCD的对角线的一交点O, 若AE=2cm, 四边形AEFB的面积为12cm2, 则CF=____, 平行四边形ABCD的面积为_____.
O
A
B
C
D
E
F
2cm
24cm2
问题思考
中心对称图形
轴对称图形
中心对称
(1) 中心对称图形和轴对称图形有什么区别?
(2) 中心对称图形和中心对称有什么区别与联系?
归纳总结
中心对称图形和轴对称图形有什么区别?
中心对称图形 轴对称图形
图形
不同点
有一个对称中心(点),
旋转前后图形全等
(对应线段、对应角相等),
旋转中心平分对应点所连线段.
有一条对称轴(直线),
对折前后图形全等
(对应线段、对应角相等)
对称轴垂直平分对应点所连线段.
归纳总结
中心对称图形和中心对称有什么区别与联系?
中心对称图形 中心对称
图形
相同点
不同点
研究对象是1个图形
研究对象是2个图形
变化形式都是图形绕对称中心旋转180°;
旋转后与原图重合(性质相同).
感悟生活
在生活中, 有许多根据中心对称图形设计出非常美丽的图案.
感悟生活
在生活中, 也有许多根据中心对称图形.
谢 谢 观 看
同课章节目录
