23.2.3 关于原点对称的点的坐标 课件(共18张PPT) 人教版数学九年级上册
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标 课件(共18张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 478.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 11:53:00 | ||
图片预览



文档简介
(共18张PPT)
第23章 旋转
23.2.3
关于原点对称的点的坐标
授课:
时间:
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
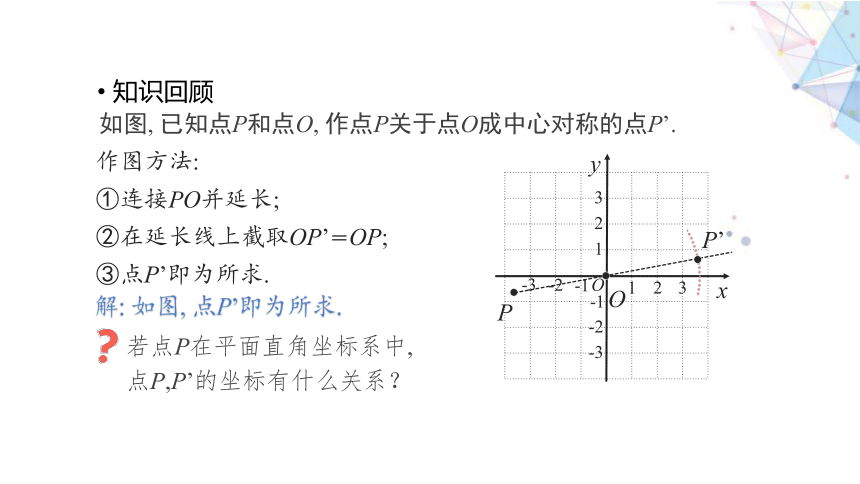
知识回顾
如图, 已知点P和点O, 作点P关于点O成中心对称的点P’.
O
P
P’
作图方法:
①连接PO并延长;
②在延长线上截取OP’=OP;
③点P’即为所求.
解: 如图, 点P’即为所求.
若点P在平面直角坐标系中, 点P,P’的坐标有什么关系?
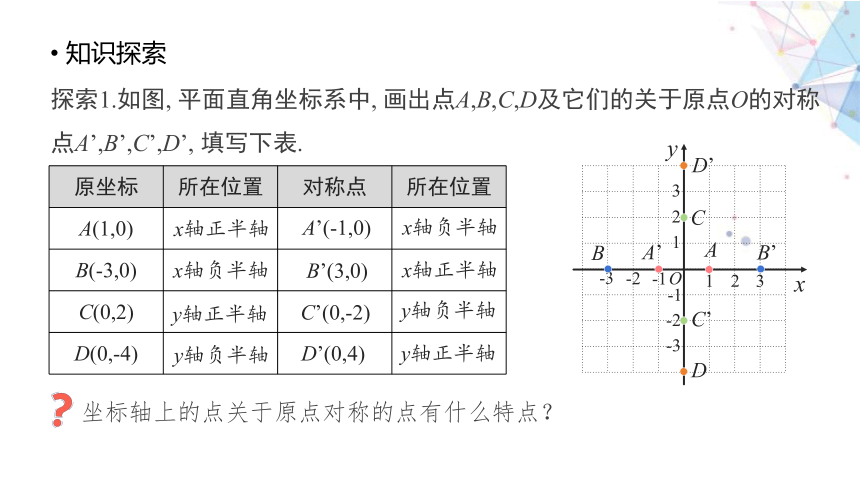
知识探索
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
探索1.如图, 平面直角坐标系中, 画出点A,B,C,D及它们的关于原点O的对称点A’,B’,C’,D’, 填写下表.
原坐标 所在位置 对称点 所在位置
A(1,0)
B(-3,0)
C(0,2)
D(0,-4)
A
A’
B
B’
C
C’
D’
D
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
A’(-1,0)
B’(3,0)
C’(0,-2)
D’(0,4)
坐标轴上的点关于原点对称的点有什么特点?
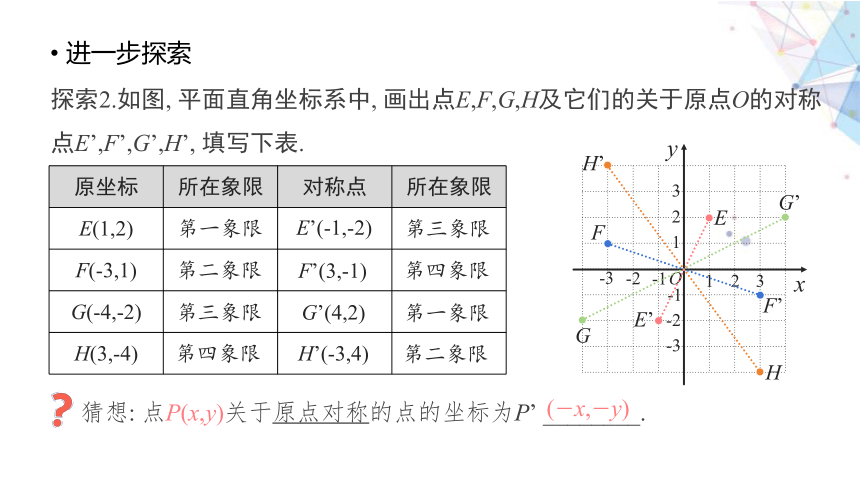
探索2.如图, 平面直角坐标系中, 画出点E,F,G,H及它们的关于原点O的对称点E’,F’,G’,H’, 填写下表.
进一步探索
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
原坐标 所在象限 对称点 所在象限
E(1,2)
F(-3,1)
G(-4,-2)
H(3,-4)
E
E’
F
F’
G
H’
H
第一象限
E’(-1,-2)
F’(3,-1)
G’(4,2)
H’(-3,4)
猜想: 点P(x,y)关于原点对称的点的坐标为P’ ________.
第二象限
第三象限
第四象限
第三象限
第四象限
第一象限
第二象限
G’
(-x,-y)
验证猜想
猜想: 点P(x,y)关于原点对称的点的坐标为P’(-x,-y).
x
y
O
P(x,y)
P’
M
N
已知: _____________________________;
求: _________.
点P, P’关于原点O对称, 且P(x,y)
P’的坐标
证明: 过点P,P’作x轴的垂线段交x轴与点M,N.
∵点P, P’关于原点O对称,
∴OP=OP’,
∵∠POM=∠P’ON,∠PMO=∠P’NO,
∴△PMO≌△P’NO(AAS)
∴PM=P’N=y,OM=ON=x,
∴P’(-x,-y).
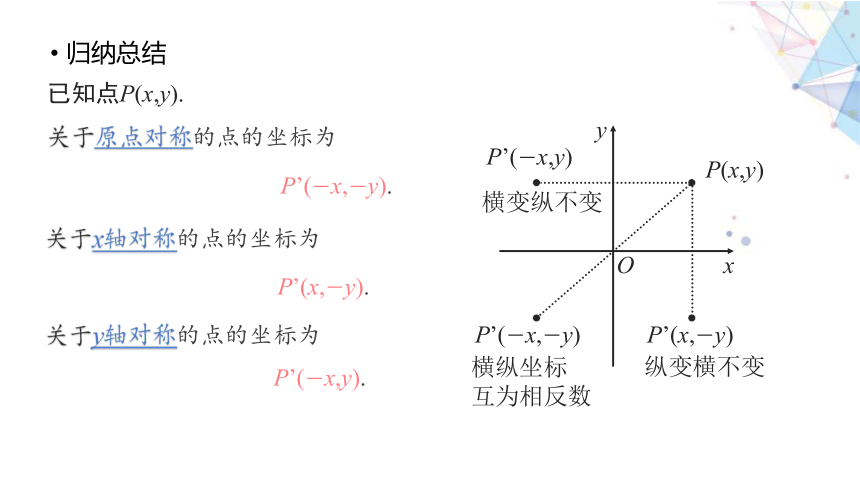
归纳总结
x
y
O
P(x,y)
P’(-x,-y)
关于原点对称的点的坐标为
已知点P(x,y).
P’(-x,-y).
关于x轴对称的点的坐标为
P’(x,-y).
关于y轴对称的点的坐标为
P’(-x,y).
P’(-x,y)
P’(x,-y)
横纵坐标
互为相反数
纵变横不变
横变纵不变
小试锋芒
练习1.平面直角坐标系内有一点P(-3,4).
(1) 点P关于x轴对称的点的坐标为________;
(2) 点P关于y轴对称的点的坐标为______;
(3) 点P关于原点对称的点的坐标为________;
(-3,-4)
(3,4)
(3,-4)
练习2.已知点A( 1,a), 点B(b,2)关于原点对称, 则a+b的值是( ).
A. 1 B. 1 C. 2 D. 2
A
小试锋芒
练习3. 已知点M(1 2m, m 1)关于原点的对称点M’在第一象限.
点M在第____象限;
(2) m的取值范围在数轴上表示正确的是( ).
三
A
B
C
D
C
典例精析
例1.如图, 作出△ABC关于原点对称的△A’B’C’.
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
O
A
B
C
(1) 写出△ABC三个顶点的坐标.
A(-2,3),B(-4,0),C(-1,-3)
(2) 如何作出△A’B’C’
∵点A,A’关于原点对称,
∴A’(2,-3),
同理B’(4,0),C’(1,3),
连接A’,B’,C’得△A’B’C’.
A’
B’
C’
思考:作关于原点对称的图形的步骤是什么?
归纳总结
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
O
A
B
C
A’
B’
C’
作关于原点对称的图形的步骤:
写出图形顶点坐标;
写出图形顶点关于原点的对称点的坐标;
描点, 连线.
小试锋芒
练习4. 已知△ABC的三个顶点坐标为A(3,-2),B(-2,2),C(-4,-2).
(1) 在平面直角坐标系中作△ABC;
(2) 作△ABC关于原点O对称的△A’B’C’;
(3) 求△A’B’C’的面积.
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
O
A
B
C
A’
B’
C’
解: (1) 如图, △ABC即为所求;
(2) 如图, △A’B’C’即为所求;
(3) △A’B’C’的面积为14.
小试锋芒
练习5. 如图, 菱形ABCD对角线交点与坐标原点O重合, 点A( 2,5), 则点C的坐标是( ).
A. (5, 2) B. (2, 5) C. (2,5) D. ( 2, 5)
B
问题探索
如图, 点P(x1,y1),P’(x2,y2)关于点M(a,b)对称.
x
y
O
P
P’
M
(1) 图中PM,P’M有怎样的数量关系;
∵点P,P’关于点M对称;
∴PM=P’M.
(2) 猜想x1,x2与a有怎样的数量关系
y1,y2与b的数量关系呢
问题探索
如图, 点P(x1,y1),P’(x2,y2)关于点M(a,b)对称.
x
y
O
P
P’
M
x1
x2
a
y2
y1
b
A
B
猜想x1,x2与a有怎样的数量关系 y1,y2与b的数量关系呢
解: 由题意易得△APM≌△BMP’,
∴AM=BP’,
∴a-x1=x2-a,得,
同理AP=BM,得.
思考:还有其它的证明方法吗?
问题探索
如图, 点P(x1,y1),P’(x2,y2)关于点M(a,b)对称.
x
y
O
P
P’
M
A
B
猜想x1,x2与a有怎样的数量关系 y1,y2与b的数量关系呢
解: 将P,P’平移至AB.
∴M(a,b)到点O(0,0),横坐标-a,纵坐标-b,
∴P(x1,y1)平移后点A的坐标为(x1-a,y1-b),
∴P’(x2,y2)平移后点B的坐标为(x2-a,y2-b),
∵点A,B关于点O对称
∴ x1-a+ x2-a=0, y1-b+ y2-b=0,
∴, .
归纳总结
如图, 若点P(x1,y1),P’(x2,y2)中点为M,
那么中点坐标为
x
y
O
P
P’
M
.
小试锋芒
练习6.已知点A(2,-5)与B(-4,1)关于点M对称, 则点M的坐标为_______.
(-1,2)
练习7.点P(1,-1)关于点N(-1,0)对称的点P’的坐标为______.
(-3,1)
谢 谢 观 看
第23章 旋转
23.2.3
关于原点对称的点的坐标
授课:
时间:
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
知识回顾
如图, 已知点P和点O, 作点P关于点O成中心对称的点P’.
O
P
P’
作图方法:
①连接PO并延长;
②在延长线上截取OP’=OP;
③点P’即为所求.
解: 如图, 点P’即为所求.
若点P在平面直角坐标系中, 点P,P’的坐标有什么关系?
知识探索
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
探索1.如图, 平面直角坐标系中, 画出点A,B,C,D及它们的关于原点O的对称点A’,B’,C’,D’, 填写下表.
原坐标 所在位置 对称点 所在位置
A(1,0)
B(-3,0)
C(0,2)
D(0,-4)
A
A’
B
B’
C
C’
D’
D
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
A’(-1,0)
B’(3,0)
C’(0,-2)
D’(0,4)
坐标轴上的点关于原点对称的点有什么特点?
探索2.如图, 平面直角坐标系中, 画出点E,F,G,H及它们的关于原点O的对称点E’,F’,G’,H’, 填写下表.
进一步探索
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
原坐标 所在象限 对称点 所在象限
E(1,2)
F(-3,1)
G(-4,-2)
H(3,-4)
E
E’
F
F’
G
H’
H
第一象限
E’(-1,-2)
F’(3,-1)
G’(4,2)
H’(-3,4)
猜想: 点P(x,y)关于原点对称的点的坐标为P’ ________.
第二象限
第三象限
第四象限
第三象限
第四象限
第一象限
第二象限
G’
(-x,-y)
验证猜想
猜想: 点P(x,y)关于原点对称的点的坐标为P’(-x,-y).
x
y
O
P(x,y)
P’
M
N
已知: _____________________________;
求: _________.
点P, P’关于原点O对称, 且P(x,y)
P’的坐标
证明: 过点P,P’作x轴的垂线段交x轴与点M,N.
∵点P, P’关于原点O对称,
∴OP=OP’,
∵∠POM=∠P’ON,∠PMO=∠P’NO,
∴△PMO≌△P’NO(AAS)
∴PM=P’N=y,OM=ON=x,
∴P’(-x,-y).
归纳总结
x
y
O
P(x,y)
P’(-x,-y)
关于原点对称的点的坐标为
已知点P(x,y).
P’(-x,-y).
关于x轴对称的点的坐标为
P’(x,-y).
关于y轴对称的点的坐标为
P’(-x,y).
P’(-x,y)
P’(x,-y)
横纵坐标
互为相反数
纵变横不变
横变纵不变
小试锋芒
练习1.平面直角坐标系内有一点P(-3,4).
(1) 点P关于x轴对称的点的坐标为________;
(2) 点P关于y轴对称的点的坐标为______;
(3) 点P关于原点对称的点的坐标为________;
(-3,-4)
(3,4)
(3,-4)
练习2.已知点A( 1,a), 点B(b,2)关于原点对称, 则a+b的值是( ).
A. 1 B. 1 C. 2 D. 2
A
小试锋芒
练习3. 已知点M(1 2m, m 1)关于原点的对称点M’在第一象限.
点M在第____象限;
(2) m的取值范围在数轴上表示正确的是( ).
三
A
B
C
D
C
典例精析
例1.如图, 作出△ABC关于原点对称的△A’B’C’.
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
O
A
B
C
(1) 写出△ABC三个顶点的坐标.
A(-2,3),B(-4,0),C(-1,-3)
(2) 如何作出△A’B’C’
∵点A,A’关于原点对称,
∴A’(2,-3),
同理B’(4,0),C’(1,3),
连接A’,B’,C’得△A’B’C’.
A’
B’
C’
思考:作关于原点对称的图形的步骤是什么?
归纳总结
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
O
A
B
C
A’
B’
C’
作关于原点对称的图形的步骤:
写出图形顶点坐标;
写出图形顶点关于原点的对称点的坐标;
描点, 连线.
小试锋芒
练习4. 已知△ABC的三个顶点坐标为A(3,-2),B(-2,2),C(-4,-2).
(1) 在平面直角坐标系中作△ABC;
(2) 作△ABC关于原点O对称的△A’B’C’;
(3) 求△A’B’C’的面积.
x
y
1
2
3
O
1
2
3
-1
-2
-3
-1
-2
-3
O
A
B
C
A’
B’
C’
解: (1) 如图, △ABC即为所求;
(2) 如图, △A’B’C’即为所求;
(3) △A’B’C’的面积为14.
小试锋芒
练习5. 如图, 菱形ABCD对角线交点与坐标原点O重合, 点A( 2,5), 则点C的坐标是( ).
A. (5, 2) B. (2, 5) C. (2,5) D. ( 2, 5)
B
问题探索
如图, 点P(x1,y1),P’(x2,y2)关于点M(a,b)对称.
x
y
O
P
P’
M
(1) 图中PM,P’M有怎样的数量关系;
∵点P,P’关于点M对称;
∴PM=P’M.
(2) 猜想x1,x2与a有怎样的数量关系
y1,y2与b的数量关系呢
问题探索
如图, 点P(x1,y1),P’(x2,y2)关于点M(a,b)对称.
x
y
O
P
P’
M
x1
x2
a
y2
y1
b
A
B
猜想x1,x2与a有怎样的数量关系 y1,y2与b的数量关系呢
解: 由题意易得△APM≌△BMP’,
∴AM=BP’,
∴a-x1=x2-a,得,
同理AP=BM,得.
思考:还有其它的证明方法吗?
问题探索
如图, 点P(x1,y1),P’(x2,y2)关于点M(a,b)对称.
x
y
O
P
P’
M
A
B
猜想x1,x2与a有怎样的数量关系 y1,y2与b的数量关系呢
解: 将P,P’平移至AB.
∴M(a,b)到点O(0,0),横坐标-a,纵坐标-b,
∴P(x1,y1)平移后点A的坐标为(x1-a,y1-b),
∴P’(x2,y2)平移后点B的坐标为(x2-a,y2-b),
∵点A,B关于点O对称
∴ x1-a+ x2-a=0, y1-b+ y2-b=0,
∴, .
归纳总结
如图, 若点P(x1,y1),P’(x2,y2)中点为M,
那么中点坐标为
x
y
O
P
P’
M
.
小试锋芒
练习6.已知点A(2,-5)与B(-4,1)关于点M对称, 则点M的坐标为_______.
(-1,2)
练习7.点P(1,-1)关于点N(-1,0)对称的点P’的坐标为______.
(-3,1)
谢 谢 观 看
同课章节目录
