24.1.2.1 垂直于弦的直径 课件(共17张PPT) 人教版数学九年级上册
文档属性
| 名称 | 24.1.2.1 垂直于弦的直径 课件(共17张PPT) 人教版数学九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 493.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 11:20:43 | ||
图片预览


文档简介
(共17张PPT)
第24章 圆
24.1.2.1
垂直于弦的直径
授课:
时间:
动手实践
准备一张圆形纸片
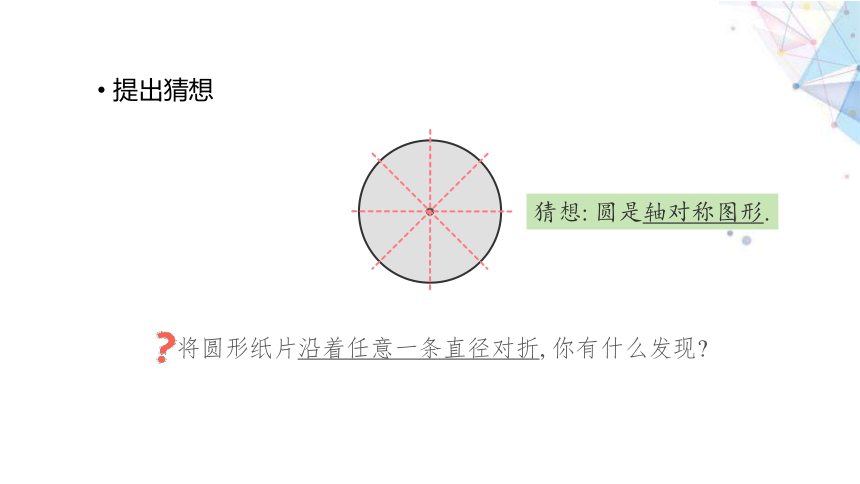
提出猜想
将圆形纸片沿着任意一条直径对折, 你有什么发现
猜想: 圆是轴对称图形.
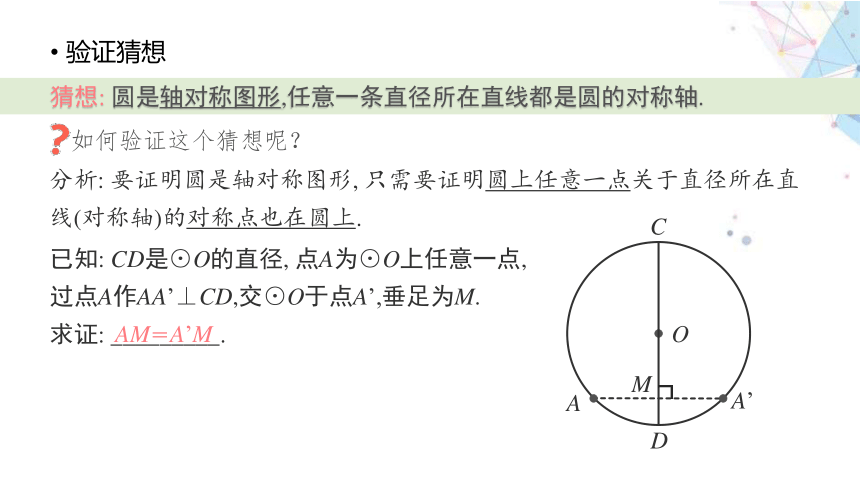
验证猜想
猜想: 圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
如何验证这个猜想呢?
分析: 要证明圆是轴对称图形, 只需要证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.
O
C
D
A
A’
M
已知: CD是⊙O的直径, 点A为⊙O上任意一点, 过点A作AA’⊥CD,交⊙O于点A’,垂足为M.
求证: _________.
AM=A’M
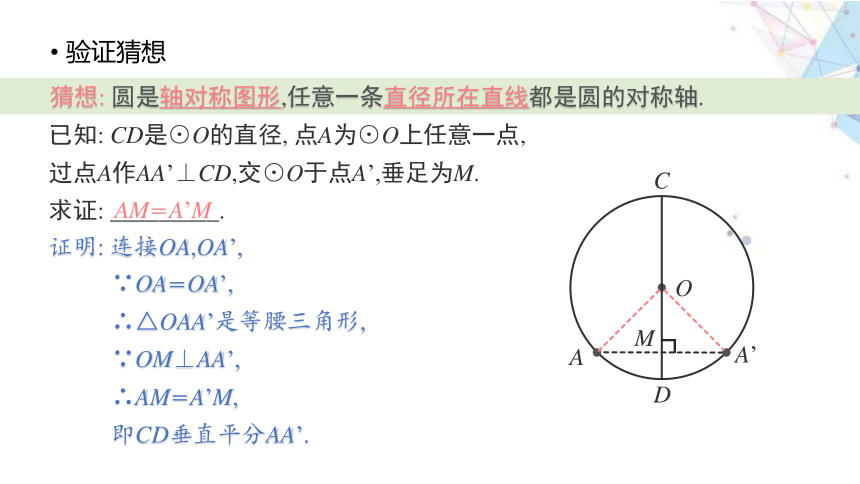
验证猜想
猜想: 圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
O
C
D
A
A’
M
已知: CD是⊙O的直径, 点A为⊙O上任意一点, 过点A作AA’⊥CD,交⊙O于点A’,垂足为M.
求证: _________.
AM=A’M
证明: 连接OA,OA’,
∵OA=OA’,
∴△OAA’是等腰三角形,
∵OM⊥AA’,
∴AM=A’M,
即CD垂直平分AA’.
得出结论
圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
O
C
D
A
A’
M
对于圆上任意一点A,在圆上都有关于直线CD的对称点A’,
因此⊙O关于直线CD对称.
将圆O沿着CD折叠时, 有哪些相等的线段和劣弧
你有什么发现
相等的线段: AM=A’M,
相等的弧: =, =.
发现: 直径平分弦AA’,并且平分, .
如何用文字语言概括?
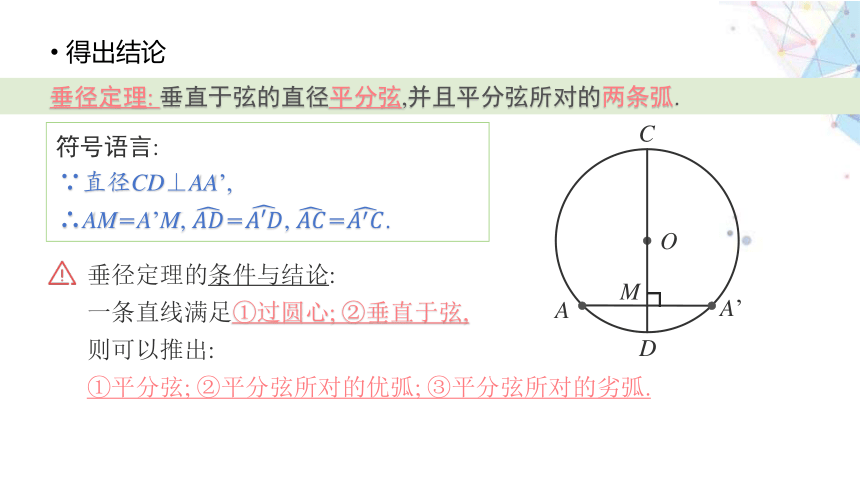
得出结论
垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
O
C
D
A
A’
M
符号语言:
∵直径CD⊥AA’,
∴AM=A’M, =, =.
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出:
①平分弦; ②平分弦所对的优弧; ③平分弦所对的劣弧.
明察秋毫
练习1.下列命题是真命题的有__个.
圆是轴对称图形;
任何一条直径所在直线都是圆的对称轴;
直径是圆的对称轴.
练习2.下列图形是否满足垂径定理的条件
2
归纳总结
垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
满足垂径定理的几种常见图形:
典例精析
例1.如右图, 直径CD⊥AB,垂足为M.
解: 连接OA,
∵直径CD⊥AB, ∴AM=AB=4,
∴圆O的半径OA==5.
O
C
D
A
B
M
(1) 若AM=2,则AB=____;
(2) 若AB=8,OM=3,求圆O的半径.
4
(3) 若圆O的半径为r,OM=d,AM=a,则a,d,r之间的数量关系为__________.
d2+a2=r2
归纳总结
如右图, r表示圆的半径; d表示圆心到弦的距离, 简称弦心距;
a表示弦长的一半; h表示弓形的高.
r
a
h
d
r,d,a,h的关系:
① r=h+d;
② r2=a2+d2.
半径2=弦长一半2+弦心距2
遇垂径, 连半径, 构造直角三角形, 利用勾股定理求解.
小试锋芒
练习3.如图, ⊙O半径为5cm, 弦AB=6cm, OC⊥AB于点C, 则OC=( ).
A. 3cm B. 4cm C. 5cm D. 6cm
B
小试锋芒
练习4.如图, 在⊙O中, AB, AC为互相垂直的两条弦, AB=8cm, AC=6cm, OD⊥AB, OE⊥AC, 垂足分别为D, E.且OD=3cm, OE=4cm, 求⊙O的半径.
答案: ⊙O的半径为5cm.
典例精析
例2.如图, 两个圆都以点O为圆心, 大圆的弦AB交小圆于C, D两点.
求证: AC=BD.
E
证明: 过点O作OE垂直于CD, 垂足为E,
∵OE⊥CD,
∴CE=DE,AE=BE,
∴AC-CE=BE-DE,
即AC=BD.
过圆心作弦的弦心距(垂线段), 或作垂直于弦的直径, 可以为应用垂径定理创造条件.
小试锋芒
练习5.如图, AB,CD是⊙O中弦, 且AB//CD.
求证: =.
E
F
G
证明: 过点O作EF垂直于AB, 垂足为F,
交⊙O于点E, 交CD于点G.
∵AB//CD,
∴EF⊥CD,
∴=, =,
∴=,
即.
小试锋芒
练习6.如图, 已知AB是⊙O的弦, 半径OA=20cm, ∠AOB=120°.
求: (1)弦AB的长; (2)△AOB的面积.
C
答案: (1) 20cm; (2)100cm2.
谢 谢 观 看
第24章 圆
24.1.2.1
垂直于弦的直径
授课:
时间:
动手实践
准备一张圆形纸片
提出猜想
将圆形纸片沿着任意一条直径对折, 你有什么发现
猜想: 圆是轴对称图形.
验证猜想
猜想: 圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
如何验证这个猜想呢?
分析: 要证明圆是轴对称图形, 只需要证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.
O
C
D
A
A’
M
已知: CD是⊙O的直径, 点A为⊙O上任意一点, 过点A作AA’⊥CD,交⊙O于点A’,垂足为M.
求证: _________.
AM=A’M
验证猜想
猜想: 圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
O
C
D
A
A’
M
已知: CD是⊙O的直径, 点A为⊙O上任意一点, 过点A作AA’⊥CD,交⊙O于点A’,垂足为M.
求证: _________.
AM=A’M
证明: 连接OA,OA’,
∵OA=OA’,
∴△OAA’是等腰三角形,
∵OM⊥AA’,
∴AM=A’M,
即CD垂直平分AA’.
得出结论
圆是轴对称图形,任意一条直径所在直线都是圆的对称轴.
O
C
D
A
A’
M
对于圆上任意一点A,在圆上都有关于直线CD的对称点A’,
因此⊙O关于直线CD对称.
将圆O沿着CD折叠时, 有哪些相等的线段和劣弧
你有什么发现
相等的线段: AM=A’M,
相等的弧: =, =.
发现: 直径平分弦AA’,并且平分, .
如何用文字语言概括?
得出结论
垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
O
C
D
A
A’
M
符号语言:
∵直径CD⊥AA’,
∴AM=A’M, =, =.
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出:
①平分弦; ②平分弦所对的优弧; ③平分弦所对的劣弧.
明察秋毫
练习1.下列命题是真命题的有__个.
圆是轴对称图形;
任何一条直径所在直线都是圆的对称轴;
直径是圆的对称轴.
练习2.下列图形是否满足垂径定理的条件
2
归纳总结
垂径定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
满足垂径定理的几种常见图形:
典例精析
例1.如右图, 直径CD⊥AB,垂足为M.
解: 连接OA,
∵直径CD⊥AB, ∴AM=AB=4,
∴圆O的半径OA==5.
O
C
D
A
B
M
(1) 若AM=2,则AB=____;
(2) 若AB=8,OM=3,求圆O的半径.
4
(3) 若圆O的半径为r,OM=d,AM=a,则a,d,r之间的数量关系为__________.
d2+a2=r2
归纳总结
如右图, r表示圆的半径; d表示圆心到弦的距离, 简称弦心距;
a表示弦长的一半; h表示弓形的高.
r
a
h
d
r,d,a,h的关系:
① r=h+d;
② r2=a2+d2.
半径2=弦长一半2+弦心距2
遇垂径, 连半径, 构造直角三角形, 利用勾股定理求解.
小试锋芒
练习3.如图, ⊙O半径为5cm, 弦AB=6cm, OC⊥AB于点C, 则OC=( ).
A. 3cm B. 4cm C. 5cm D. 6cm
B
小试锋芒
练习4.如图, 在⊙O中, AB, AC为互相垂直的两条弦, AB=8cm, AC=6cm, OD⊥AB, OE⊥AC, 垂足分别为D, E.且OD=3cm, OE=4cm, 求⊙O的半径.
答案: ⊙O的半径为5cm.
典例精析
例2.如图, 两个圆都以点O为圆心, 大圆的弦AB交小圆于C, D两点.
求证: AC=BD.
E
证明: 过点O作OE垂直于CD, 垂足为E,
∵OE⊥CD,
∴CE=DE,AE=BE,
∴AC-CE=BE-DE,
即AC=BD.
过圆心作弦的弦心距(垂线段), 或作垂直于弦的直径, 可以为应用垂径定理创造条件.
小试锋芒
练习5.如图, AB,CD是⊙O中弦, 且AB//CD.
求证: =.
E
F
G
证明: 过点O作EF垂直于AB, 垂足为F,
交⊙O于点E, 交CD于点G.
∵AB//CD,
∴EF⊥CD,
∴=, =,
∴=,
即.
小试锋芒
练习6.如图, 已知AB是⊙O的弦, 半径OA=20cm, ∠AOB=120°.
求: (1)弦AB的长; (2)△AOB的面积.
C
答案: (1) 20cm; (2)100cm2.
谢 谢 观 看
同课章节目录
