24.1.3. 弧、弦、圆心角 课件(共19张PPT) 人教版数学九年级上册
文档属性
| 名称 | 24.1.3. 弧、弦、圆心角 课件(共19张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 768.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 11:24:03 | ||
图片预览



文档简介
(共19张PPT)
第24章 圆
24.1.3
弧、弦、圆心角
授课:
时间:
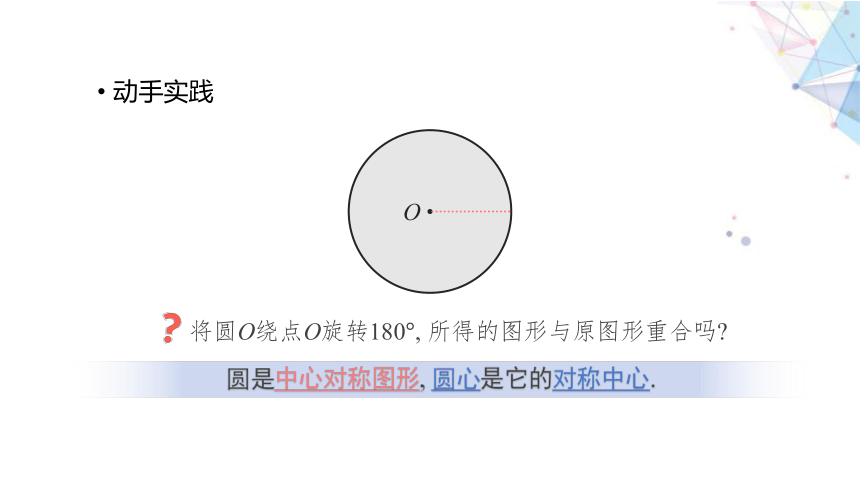
动手实践
O
将圆O绕点O旋转180°, 所得的图形与原图形重合吗
圆是中心对称图形, 圆心是它的对称中心.
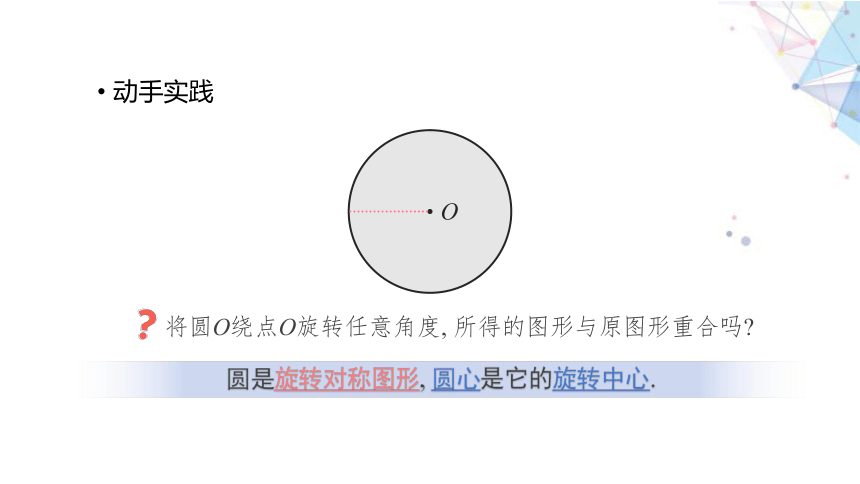
动手实践
O
将圆O绕点O旋转任意角度, 所得的图形与原图形重合吗
圆是旋转对称图形, 圆心是它的旋转中心.
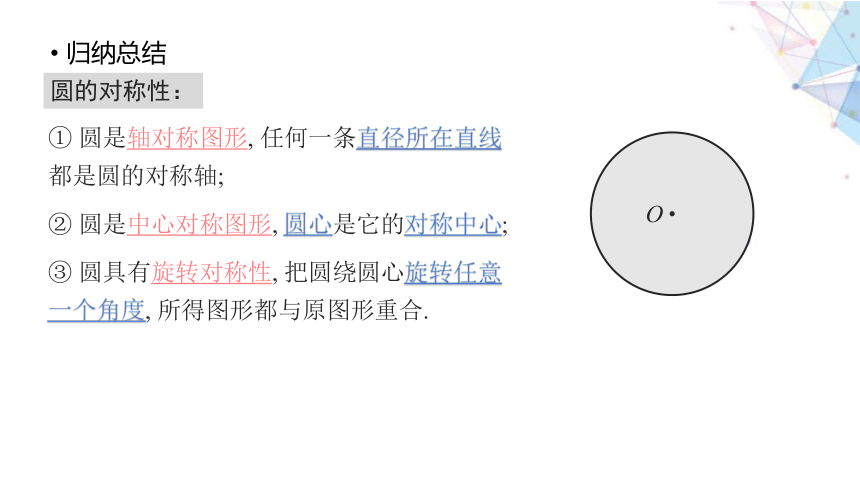
归纳总结
O
圆的对称性:
① 圆是轴对称图形, 任何一条直径所在直线都是圆的对称轴;
② 圆是中心对称图形, 圆心是它的对称中心;
③ 圆具有旋转对称性, 把圆绕圆心旋转任意一个角度, 所得图形都与原图形重合.
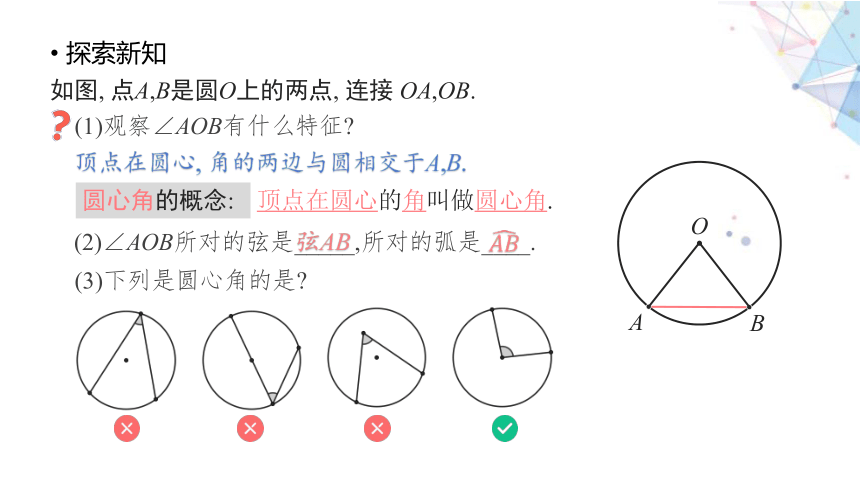
探索新知
O
如图, 点A,B是圆O上的两点, 连接 OA,OB.
A
B
(1)观察∠AOB有什么特征
顶点在圆心, 角的两边与圆相交于A,B.
圆心角的概念:
顶点在圆心的角叫做圆心角.
(2)∠AOB所对的弦是_____,所对的弧是____.
弦AB
(3)下列是圆心角的是
问题探索
O
如图, 在⊙O中, ∠AOB=∠A’OB’.
A
B
A’
B’
(1)∠AOB所对的弦是_____,所对的弧是____,
∠A’OB’所对的弦是______,所对的弧是_____;
(2) 弦AB和弦A’B’有怎样的数量关系 和呢
弦AB
弦A’B’
弦AB=弦A’B’, =.
(3) 如何证明呢?
问题探索
O
如图, 在⊙O中, ∠AOB=∠A’OB’.
A’(A)
B’(B)
(3) 如何证明呢?
解: 将∠AOB连同绕圆心O旋转, 使射线OA与OA’重合,
∵∠AOB=∠A’OB’,
∴射线OB与____重合,
又 OA=_____,OB=_____,
∴点A与点___重合, 点B与点___重合,
∴AB与____重合, 与_____重合,
即AB=_____, =_____.
OB’
OA’
OB’
A’
B’
A’B’
A’B’
(4) 在等圆中成立吗?如何用文字语言概括这个发现
探索新知
O
A
B
A’
B’
在同圆或等圆中, 如果圆心角相等, 那么它们所对的弧相等, 所对的弦也相等.
符号语言:
∵∠AOB=∠A’OB’,
∴AB=A’B’, =.
(1) 条件中“在同圆或等圆中”能否去掉
(2) 条件: ①∠AOB=∠A’OB’,
可以推出: ②AB=A’B’; ③=.
能否由②推出①③, 或由③推出①②
探索新知
定理: 在同圆或等圆中, 如果圆心角相等, 那么它们所对的弧相等, 所对的弦也相等.
推论1: 在同圆或等圆中, 如果两条弧相等, 那么它们所对的圆心角相等, 所对的弦相等.
推论2: 在同圆或等圆中, 如果两条弦相等, 那么它们所对的圆心角相等, 所对的优弧和劣弧分别相等.
弧、弦、圆心角的关系定理及推论:
O
A
B
A’
B’
归纳总结
弧、弦、圆心角的关系
圆心角相等
∠AOB=∠A’OB’
弧相等
=
弦相等
AB=A’B’
O
A
B
A’
B’
典例精析
例1. 如图, 在⊙O中, = ,∠ACB=60°.
求证: ∠AOB=∠BOC=∠AOC.
证明: ∵ = ,
∴AB=AC,△ABC是等腰三角形,
∵∠ACB=60°
∴ △ABC是等边三角形,
∴AB=AC=BC,
∴∠AOB=∠BOC=∠AOC.
小试锋芒
练习1.如图, AB,CD是圆O的两条弦.
(1) 如果AB=CD,那么________,_______________;
(2) 如果=,那么________,_______________;
(3) 如果∠AOB=∠COD,那么________,________;
(4) 如果AB=CD,OE⊥AB,OF⊥CD, 垂足为E,F,
猜想OE,OF的数量关系, 并证明.
=
∠AOB=∠COD
AB=CD
∠AOB=∠COD
AB=CD
=
答案: OE=OF,可根据垂径定理和全等三角形解答.
小试锋芒
练习2.如图, AB是⊙O 的直径, ==.∠AOE=75°, 求∠BOD 的度数.
答案: ∠BOD=70°.
问题思考
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出: ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
(1)什么是垂径定理?它的条件与结论是什么?
(2)若一条直线满足①⑤, 能推出②③④吗
问题思考
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出: ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
(2)若一条直线满足①⑤, 能推出②③④吗
O
C
D
A
B
M
已知:____________________________________.
求证: ________________________.
如图, 圆O的直径CD平分,交AB于点M
CD⊥AB,AM=BM,=
证明: 连接OA,OB, 则OA=OB,
∴△OAB是等腰三角形,
∵ =, ∴∠AOD=∠BOD,
∴CD⊥AB, AM=BM,
∴ =.
归纳总结
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出: ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
(3)以上条件中, 任意知道其中两个可以推出其余三个吗
垂径定理及垂径定理推论:
若一条直线满足
①过圆心; ②垂直于弦; ③平分弦;
④平分弦所对的优弧; ⑤平分弦所对的劣弧.
其中任意两个, 便可推出其它三个, 即“知二推三”.
典例精析
例2.如图, AB为⊙O的直径, C, D为⊙O上的两点, 且C为的中点, 若∠BAD=20°, 求∠ACO的度数.
证明: ∵ = , OC为半径,
∴AE⊥OC,
∴∠AOE=90°-20°=70°,
∵OC=OA,
∴∠ACO==55°.
小试锋芒
练习3.如图, AB是⊙O的直径, BC是弦, 点E是的中点, OE交BC于点D, 连结AC, 若BC=6, DE=1, 求AC的长.
答案: AC=8.
谢 谢 观 看
第24章 圆
24.1.3
弧、弦、圆心角
授课:
时间:
动手实践
O
将圆O绕点O旋转180°, 所得的图形与原图形重合吗
圆是中心对称图形, 圆心是它的对称中心.
动手实践
O
将圆O绕点O旋转任意角度, 所得的图形与原图形重合吗
圆是旋转对称图形, 圆心是它的旋转中心.
归纳总结
O
圆的对称性:
① 圆是轴对称图形, 任何一条直径所在直线都是圆的对称轴;
② 圆是中心对称图形, 圆心是它的对称中心;
③ 圆具有旋转对称性, 把圆绕圆心旋转任意一个角度, 所得图形都与原图形重合.
探索新知
O
如图, 点A,B是圆O上的两点, 连接 OA,OB.
A
B
(1)观察∠AOB有什么特征
顶点在圆心, 角的两边与圆相交于A,B.
圆心角的概念:
顶点在圆心的角叫做圆心角.
(2)∠AOB所对的弦是_____,所对的弧是____.
弦AB
(3)下列是圆心角的是
问题探索
O
如图, 在⊙O中, ∠AOB=∠A’OB’.
A
B
A’
B’
(1)∠AOB所对的弦是_____,所对的弧是____,
∠A’OB’所对的弦是______,所对的弧是_____;
(2) 弦AB和弦A’B’有怎样的数量关系 和呢
弦AB
弦A’B’
弦AB=弦A’B’, =.
(3) 如何证明呢?
问题探索
O
如图, 在⊙O中, ∠AOB=∠A’OB’.
A’(A)
B’(B)
(3) 如何证明呢?
解: 将∠AOB连同绕圆心O旋转, 使射线OA与OA’重合,
∵∠AOB=∠A’OB’,
∴射线OB与____重合,
又 OA=_____,OB=_____,
∴点A与点___重合, 点B与点___重合,
∴AB与____重合, 与_____重合,
即AB=_____, =_____.
OB’
OA’
OB’
A’
B’
A’B’
A’B’
(4) 在等圆中成立吗?如何用文字语言概括这个发现
探索新知
O
A
B
A’
B’
在同圆或等圆中, 如果圆心角相等, 那么它们所对的弧相等, 所对的弦也相等.
符号语言:
∵∠AOB=∠A’OB’,
∴AB=A’B’, =.
(1) 条件中“在同圆或等圆中”能否去掉
(2) 条件: ①∠AOB=∠A’OB’,
可以推出: ②AB=A’B’; ③=.
能否由②推出①③, 或由③推出①②
探索新知
定理: 在同圆或等圆中, 如果圆心角相等, 那么它们所对的弧相等, 所对的弦也相等.
推论1: 在同圆或等圆中, 如果两条弧相等, 那么它们所对的圆心角相等, 所对的弦相等.
推论2: 在同圆或等圆中, 如果两条弦相等, 那么它们所对的圆心角相等, 所对的优弧和劣弧分别相等.
弧、弦、圆心角的关系定理及推论:
O
A
B
A’
B’
归纳总结
弧、弦、圆心角的关系
圆心角相等
∠AOB=∠A’OB’
弧相等
=
弦相等
AB=A’B’
O
A
B
A’
B’
典例精析
例1. 如图, 在⊙O中, = ,∠ACB=60°.
求证: ∠AOB=∠BOC=∠AOC.
证明: ∵ = ,
∴AB=AC,△ABC是等腰三角形,
∵∠ACB=60°
∴ △ABC是等边三角形,
∴AB=AC=BC,
∴∠AOB=∠BOC=∠AOC.
小试锋芒
练习1.如图, AB,CD是圆O的两条弦.
(1) 如果AB=CD,那么________,_______________;
(2) 如果=,那么________,_______________;
(3) 如果∠AOB=∠COD,那么________,________;
(4) 如果AB=CD,OE⊥AB,OF⊥CD, 垂足为E,F,
猜想OE,OF的数量关系, 并证明.
=
∠AOB=∠COD
AB=CD
∠AOB=∠COD
AB=CD
=
答案: OE=OF,可根据垂径定理和全等三角形解答.
小试锋芒
练习2.如图, AB是⊙O 的直径, ==.∠AOE=75°, 求∠BOD 的度数.
答案: ∠BOD=70°.
问题思考
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出: ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
(1)什么是垂径定理?它的条件与结论是什么?
(2)若一条直线满足①⑤, 能推出②③④吗
问题思考
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出: ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
(2)若一条直线满足①⑤, 能推出②③④吗
O
C
D
A
B
M
已知:____________________________________.
求证: ________________________.
如图, 圆O的直径CD平分,交AB于点M
CD⊥AB,AM=BM,=
证明: 连接OA,OB, 则OA=OB,
∴△OAB是等腰三角形,
∵ =, ∴∠AOD=∠BOD,
∴CD⊥AB, AM=BM,
∴ =.
归纳总结
垂径定理的条件与结论:
一条直线满足①过圆心; ②垂直于弦,
则可以推出: ③平分弦; ④平分弦所对的优弧; ⑤平分弦所对的劣弧.
(3)以上条件中, 任意知道其中两个可以推出其余三个吗
垂径定理及垂径定理推论:
若一条直线满足
①过圆心; ②垂直于弦; ③平分弦;
④平分弦所对的优弧; ⑤平分弦所对的劣弧.
其中任意两个, 便可推出其它三个, 即“知二推三”.
典例精析
例2.如图, AB为⊙O的直径, C, D为⊙O上的两点, 且C为的中点, 若∠BAD=20°, 求∠ACO的度数.
证明: ∵ = , OC为半径,
∴AE⊥OC,
∴∠AOE=90°-20°=70°,
∵OC=OA,
∴∠ACO==55°.
小试锋芒
练习3.如图, AB是⊙O的直径, BC是弦, 点E是的中点, OE交BC于点D, 连结AC, 若BC=6, DE=1, 求AC的长.
答案: AC=8.
谢 谢 观 看
同课章节目录
