24.1.4.1 圆周角定理 课件(共18张PPT) 人教版数学九年级上册
文档属性
| 名称 | 24.1.4.1 圆周角定理 课件(共18张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 810.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第24章 圆
24.1.4.1
圆周角定理
授课:
时间:
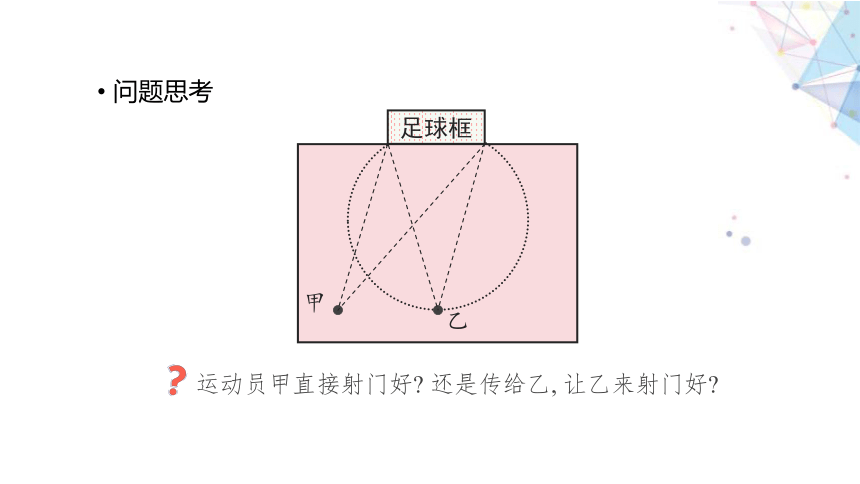
问题思考
甲
足球框
运动员甲直接射门好 还是传给乙, 让乙来射门好
乙
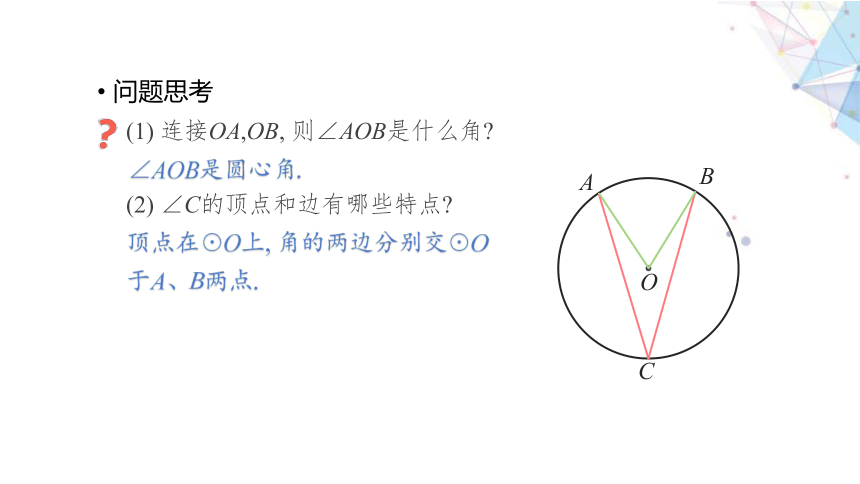
问题思考
C
A
B
O
(1) 连接OA,OB, 则∠AOB是什么角
顶点在☉O上, 角的两边分别交☉O于A、B两点.
(2) ∠C的顶点和边有哪些特点
∠AOB是圆心角.
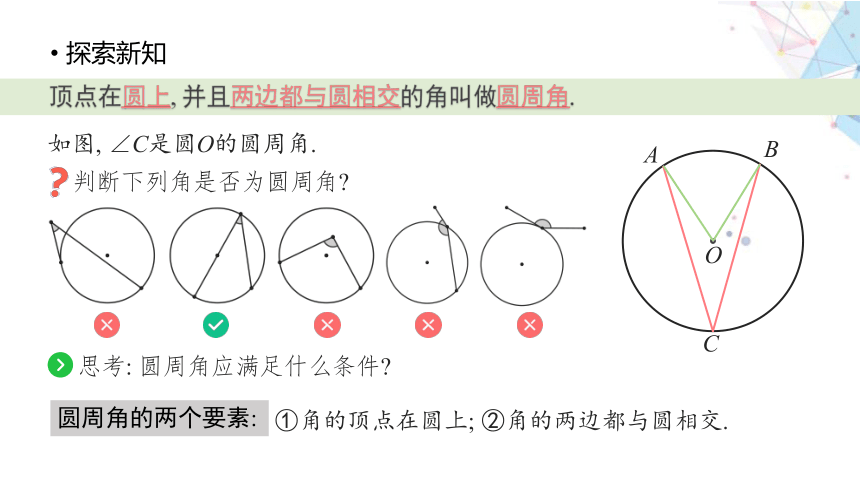
探索新知
顶点在圆上, 并且两边都与圆相交的角叫做圆周角.
判断下列角是否为圆周角
C
A
B
O
如图, ∠C是圆O的圆周角.
思考: 圆周角应满足什么条件
①角的顶点在圆上; ②角的两边都与圆相交.
圆周角的两个要素:
探索新知
如图, ∠C是圆O的圆周角.
C
A
B
O
(1)∠AOB所对的弦是_____,所对的弧是____;
∠C所对的弦是_____,所对的弧是____;
(2) 同弧所对的圆心角和圆周角有什么区别与联系?
弦AB
弦AB
(3)你还能画出所对的其它圆周角吗 有多少个?
这些圆周角与圆心O有哪些位置关系
圆心角 圆周角
区别
联系
顶点在圆心
顶点在圆上
角的两边都与圆相交.
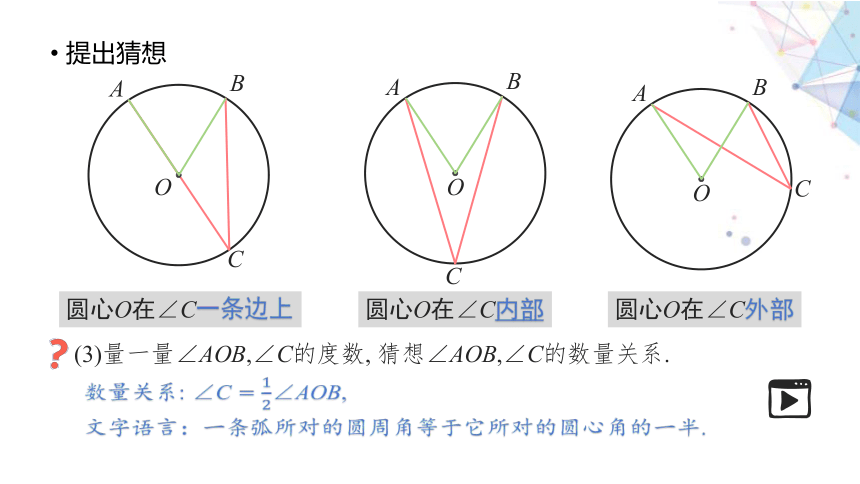
提出猜想
C
A
B
O
C
A
B
O
圆心O在∠C一条边上
圆心O在∠C外部
(3)量一量∠AOB,∠C的度数, 猜想∠AOB,∠C的数量关系.
数量关系: ∠C = ∠AOB,
文字语言:一条弧所对的圆周角等于它所对的圆心角的一半.
C
A
B
O
圆心O在∠C内部
验证猜想
猜想: 一条弧所对的圆周角等于它所对的圆心角的一半.
证明: ∵OB=OC,
∴∠B=∠C,
∵∠AOB=∠B+∠C,
∴∠AOB=2∠C,
即∠C=∠AOB.
C
A
B
O
(4)当圆心O在∠C一条边上时, 如何证明∠C=∠AOB
(5)当圆心O在∠C内部或外部时, 如何证明
验证猜想
C
A
B
O
C
A
B
O
圆心O在∠C一条边上
圆心O在∠C外部
C
A
B
O
圆心O在∠C内部
猜想: 一条弧所对的圆周角等于它所对的圆心角的一半.
D
D
得出结论
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
C
A
B
O
符号语言:
∵,
∴∠C=∠AOB(∠AOB=2∠C).
练习1.如右图, 填空.
(1)若∠AOB=50°, 则∠C=____;
(2)若∠C=26°, 则∠AOB =____.
25°
52°
典例精析
例1.如图, 圆O的直径CD⊥AB, 垂足为M,连接OA,BC, 若∠C=30°, 求∠AOD.
解:连接OB,
∵ =,
∴ ∠BOD=2∠C=60°,
∵直径CD⊥AB,
∴ =,
∴∠AOD=∠BOD=60°.
等弧所对的圆心角与圆周角有什么关系
同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.
小试锋芒
练习2.如图, 点A, B, C都在⊙O上.若∠AOB=50°, ∠B=55°, 求∠A.
答案:∠A=30°.
进一步探索
如图, 在圆O中, ∠O=60°.
解: ∠C1=∠C2=∠C3= ∠O=30°.
(1)∠C1, ∠C2, ∠C3所对的弧是_____;
(2)如何求∠C1, ∠C2, ∠C3的度数
(3)同弧所对的圆周角有怎样的数量关系?
等弧有这样的数量关系吗?
得出结论
圆周角定理的推论1: 同弧或等弧所对的圆周角相等.
符号语言:
∵,
∴∠C1=∠C2=∠C3 .
小试锋芒
练习3.如图, A,B,C,D是圆O上的四个点, 连接AB,BC,CD,AD,AC,BD.
说一说图中有哪些相等的角
答案: 对应的圆周角: ∠6=∠3,
对应的圆周角: ∠1=∠4,
对应的圆周角: ∠2=∠7,
对应的圆周角: ∠5=∠8.
典例精析
例2.如图所示, ⊙O中, 弦AB与CD相交于点E, AB=CD, 连接AD, BC.
求证: (1) = ; (2)AE=CE.
证明:(1)∵AB=CD,
∴ ,
∴ ,
即 .
(2)∵,
∴∠D=∠B,
∵AD=BC,∠AED=∠CEB,
∴△AED≌△CEB(AAS),
∴AE=CE.
小试锋芒
练习4.如图, AB是⊙O的直径, CD是⊙O的一条弦, 且CD⊥AB于点E.
(1)求证: ∠BCO=∠D;
(2)若CD=, OE=1, 求⊙O的半径.
答案:(1) 证明略; (2) 半径为3.
问题回顾
甲
足球框
运动员甲直接射门好 还是传给乙, 让乙来射门好
乙
因为甲的射门角度比乙小, 所以传给乙, 让乙来射门更好.
谢 谢 观 看
第24章 圆
24.1.4.1
圆周角定理
授课:
时间:
问题思考
甲
足球框
运动员甲直接射门好 还是传给乙, 让乙来射门好
乙
问题思考
C
A
B
O
(1) 连接OA,OB, 则∠AOB是什么角
顶点在☉O上, 角的两边分别交☉O于A、B两点.
(2) ∠C的顶点和边有哪些特点
∠AOB是圆心角.
探索新知
顶点在圆上, 并且两边都与圆相交的角叫做圆周角.
判断下列角是否为圆周角
C
A
B
O
如图, ∠C是圆O的圆周角.
思考: 圆周角应满足什么条件
①角的顶点在圆上; ②角的两边都与圆相交.
圆周角的两个要素:
探索新知
如图, ∠C是圆O的圆周角.
C
A
B
O
(1)∠AOB所对的弦是_____,所对的弧是____;
∠C所对的弦是_____,所对的弧是____;
(2) 同弧所对的圆心角和圆周角有什么区别与联系?
弦AB
弦AB
(3)你还能画出所对的其它圆周角吗 有多少个?
这些圆周角与圆心O有哪些位置关系
圆心角 圆周角
区别
联系
顶点在圆心
顶点在圆上
角的两边都与圆相交.
提出猜想
C
A
B
O
C
A
B
O
圆心O在∠C一条边上
圆心O在∠C外部
(3)量一量∠AOB,∠C的度数, 猜想∠AOB,∠C的数量关系.
数量关系: ∠C = ∠AOB,
文字语言:一条弧所对的圆周角等于它所对的圆心角的一半.
C
A
B
O
圆心O在∠C内部
验证猜想
猜想: 一条弧所对的圆周角等于它所对的圆心角的一半.
证明: ∵OB=OC,
∴∠B=∠C,
∵∠AOB=∠B+∠C,
∴∠AOB=2∠C,
即∠C=∠AOB.
C
A
B
O
(4)当圆心O在∠C一条边上时, 如何证明∠C=∠AOB
(5)当圆心O在∠C内部或外部时, 如何证明
验证猜想
C
A
B
O
C
A
B
O
圆心O在∠C一条边上
圆心O在∠C外部
C
A
B
O
圆心O在∠C内部
猜想: 一条弧所对的圆周角等于它所对的圆心角的一半.
D
D
得出结论
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
C
A
B
O
符号语言:
∵,
∴∠C=∠AOB(∠AOB=2∠C).
练习1.如右图, 填空.
(1)若∠AOB=50°, 则∠C=____;
(2)若∠C=26°, 则∠AOB =____.
25°
52°
典例精析
例1.如图, 圆O的直径CD⊥AB, 垂足为M,连接OA,BC, 若∠C=30°, 求∠AOD.
解:连接OB,
∵ =,
∴ ∠BOD=2∠C=60°,
∵直径CD⊥AB,
∴ =,
∴∠AOD=∠BOD=60°.
等弧所对的圆心角与圆周角有什么关系
同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.
小试锋芒
练习2.如图, 点A, B, C都在⊙O上.若∠AOB=50°, ∠B=55°, 求∠A.
答案:∠A=30°.
进一步探索
如图, 在圆O中, ∠O=60°.
解: ∠C1=∠C2=∠C3= ∠O=30°.
(1)∠C1, ∠C2, ∠C3所对的弧是_____;
(2)如何求∠C1, ∠C2, ∠C3的度数
(3)同弧所对的圆周角有怎样的数量关系?
等弧有这样的数量关系吗?
得出结论
圆周角定理的推论1: 同弧或等弧所对的圆周角相等.
符号语言:
∵,
∴∠C1=∠C2=∠C3 .
小试锋芒
练习3.如图, A,B,C,D是圆O上的四个点, 连接AB,BC,CD,AD,AC,BD.
说一说图中有哪些相等的角
答案: 对应的圆周角: ∠6=∠3,
对应的圆周角: ∠1=∠4,
对应的圆周角: ∠2=∠7,
对应的圆周角: ∠5=∠8.
典例精析
例2.如图所示, ⊙O中, 弦AB与CD相交于点E, AB=CD, 连接AD, BC.
求证: (1) = ; (2)AE=CE.
证明:(1)∵AB=CD,
∴ ,
∴ ,
即 .
(2)∵,
∴∠D=∠B,
∵AD=BC,∠AED=∠CEB,
∴△AED≌△CEB(AAS),
∴AE=CE.
小试锋芒
练习4.如图, AB是⊙O的直径, CD是⊙O的一条弦, 且CD⊥AB于点E.
(1)求证: ∠BCO=∠D;
(2)若CD=, OE=1, 求⊙O的半径.
答案:(1) 证明略; (2) 半径为3.
问题回顾
甲
足球框
运动员甲直接射门好 还是传给乙, 让乙来射门好
乙
因为甲的射门角度比乙小, 所以传给乙, 让乙来射门更好.
谢 谢 观 看
同课章节目录
