2025年秋沪科版八年级数学上册 第15章 轴对称图形和等腰三角形 综合测试卷(含答案)
文档属性
| 名称 | 2025年秋沪科版八年级数学上册 第15章 轴对称图形和等腰三角形 综合测试卷(含答案) | 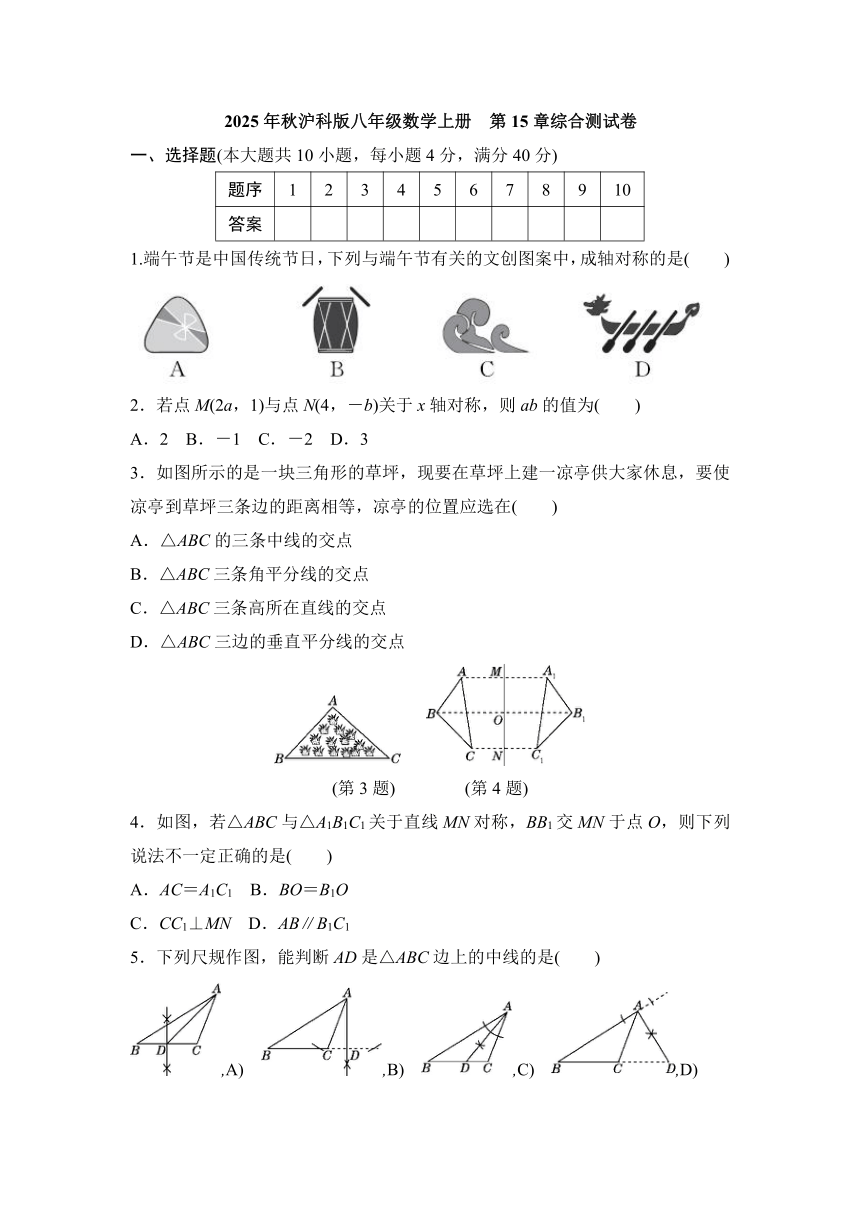 | |
| 格式 | docx | ||
| 文件大小 | 99.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 07:29:21 | ||
图片预览




文档简介
2025年秋沪科版八年级数学上册 第15章综合测试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
题序 1 2 3 4 5 6 7 8 9 10
答案
1.端午节是中国传统节日,下列与端午节有关的文创图案中,成轴对称的是( )
2.若点M(2a,1)与点N(4,-b)关于x轴对称,则ab的值为( )
A.2 B.-1 C.-2 D.3
3.如图所示的是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三边的垂直平分线的交点
(第3题) (第4题)
4.如图,若△ABC与△A1B1C1关于直线MN对称,BB1交MN于点O,则下列说法不一定正确的是( )
A.AC=A1C1 B.BO=B1O
C.CC1⊥MN D.AB∥B1C1
5.下列尺规作图,能判断AD是△ABC边上的中线的是( )
,A) ,B) ,C) ,D)
6.如图是通过折纸制作五角星的过程,则下列结论错误的是( )
A.∠1=∠2 B.∠1=∠3 C.∠1=∠4 D.∠3=∠2
7.如图,△ABC是等边三角形,D是AC的中点,DE⊥BC,CE=3,则△ABC的周长为( )
A.12 B.24 C.36 D.48
(第7题) (第8题) (第9题)
8.如图,在四边形ABDC中,对角线AD平分∠BAC,∠ACD=138°,∠ACB+∠BCD=90°,则∠ADB的度数为( )
A.42° B.48° C.50° D.53°
9.如图,在△ABC中,AB=AC=13,AD=12,BC=10,AD平分∠BAC,E是线段AC上的动点,P是线段AD上的动点,则PC+PE的最小值为( )
A. B. C. D.
10.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,F是CB延长线上一点,AF⊥CF,垂足为F,下列结论:①BC=DE;②AF=CF;③四边形ABCD的面积等于AC2;④S△BCD=S△ABF+S△ADE,其中正确的是( )
A.①② B.②③ C.①②③ D.①②③④
(第10题) (第11题) (第12题)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图所示的图形为轴对称图形,该图形的对称轴的条数为__________.
12.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=4,BC=5,S△ABC=6,则DE的长为______.
13.如图,CD是等边三角形ABC边AB上的中线,AC的垂直平分线交AC于点E,交CD于点F.若DF=1,则CD的长为________.
(第13题) (第14题)
14.如图,在△ABC中,AB=BC,D是BC上一点,DE⊥AB于点E,DF⊥BC,交AC于点F,连接BF.
(1)若∠AFD=145°,则∠EDF=________;
(2)若F是AC的中点,则∠ABC与∠CFD之间的数量关系为______________.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,在平面直角坐标系中,网格上的每个小正方形的边长均为1,△ABC的顶点坐标分别为A(-1,0),B(-3,3),C(-5,1).
(1)在图中画出△ABC关于y轴对称的△DEF(点A,B,C的对应点分别为点D,E,F);
(2)在(1)的条件下,写出点D,E,F的坐标.
16.如图,已知AB=DC,∠A=∠D,AC与DB相交于点O,求证:∠OBC=∠OCB.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在Rt△ACB中,∠C=90°,∠B=30°,点E在BC上,作ED⊥AB于点D,且EC=ED.求证:D为AB的中点.
18.如图,已知在△ABC中,点D在边AC上,且AB=AD,∠B=2∠C.
(1)尺规作图:作∠BAC的平分线AP,交BC于点P;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:点D在线段PC的垂直平分线上.
五、(本大题共2小题,每小题10分,满分20分)
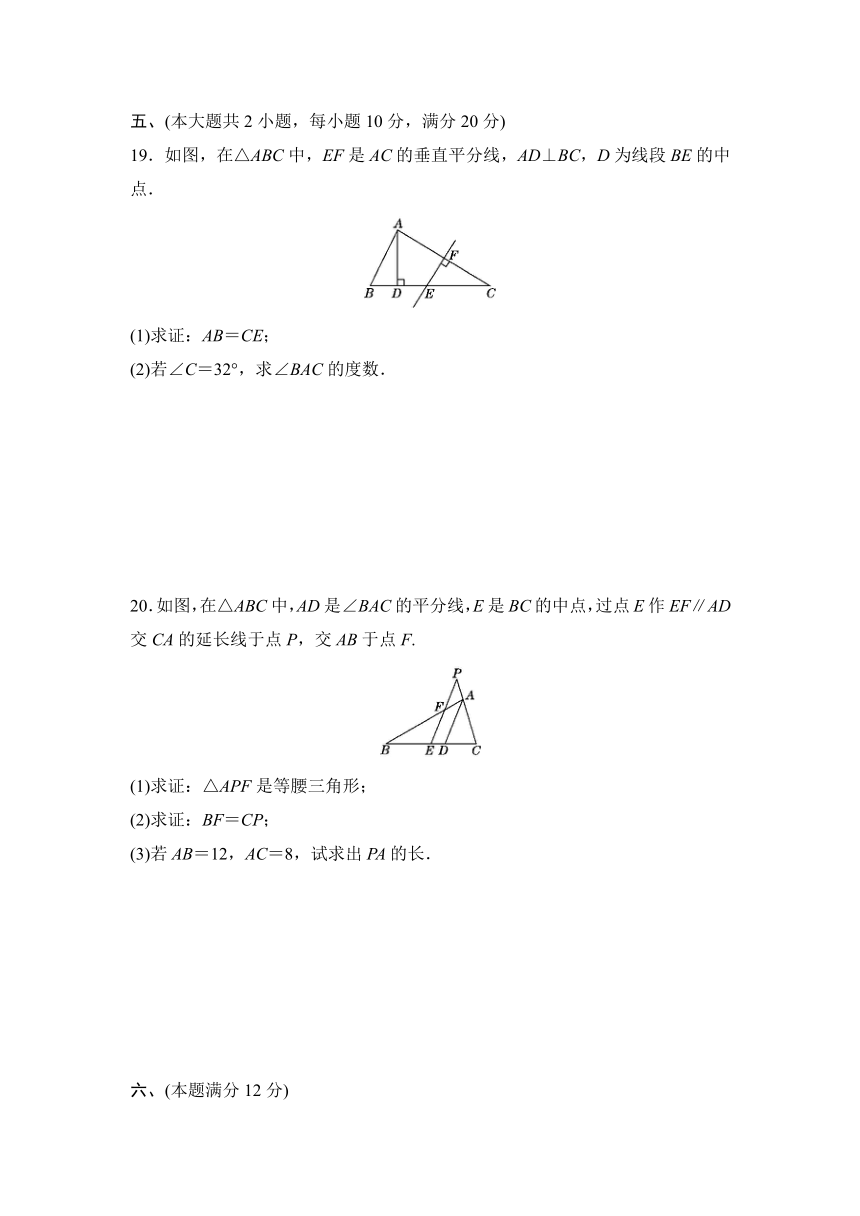
19.如图,在△ABC中,EF是AC的垂直平分线,AD⊥BC,D为线段BE的中点.
(1)求证:AB=CE;
(2)若∠C=32°,求∠BAC的度数.
20.如图,在△ABC中,AD是∠BAC的平分线,E是BC的中点,过点E作EF∥AD交CA的延长线于点P,交AB于点F.
(1)求证:△APF是等腰三角形;
(2)求证:BF=CP;
(3)若AB=12,AC=8,试求出PA的长.
六、(本题满分12分)
21.如图,灯塔C在海岛A 的北偏东75°的方向,某天9时,一艘船从海岛A 出发,以30 n mile/h的速度向东航行,11时到达 B 处,此时测得灯塔C在B 处的北偏东60°的方向.
(1)求∠C的度数;
(2)已知在以灯塔C为中心,周围25 n mile的范围内均有暗礁,若该船继续向东航行,是否有触礁的危险?请说明理由.
七、(本题满分12分)
22.我们定义:在四边形ABCD中,如果∠A=α(0°<α<180°),∠C=180°-α,对角线BD平分∠ABC,我们称这种四边形为“分角对补四边形”.
【特例感知】(1)如图①,当α=90°时,由角平分线的性质可得DA=__________;
【猜想论证】(2)如图②,当α为任意度数时,猜想DA与DC的数量关系,并给予证明;
【探究应用】(3)请利用(2)中的结论解决问题:如图③,在△ABC中,AB=AC,∠BAC=100°.BD平分∠ABC,求证:BD+AD=BC.
八、(本题满分14分)
23.如图①,已知等边三角形ABC,P,Q分别是边AB,BC上的动点(端点除外),点P,Q分别从顶点A,B同时出发,向点B,C运动,且它们的运动速度相同,AQ,CP交于点M.
(1)求证:AQ=CP;
(2)当点P,Q分别在AB,BC边上运动时,∠QMC的大小变化吗?若变化,请说明理由;若不变,请直接写出它的度数;
(3)如图②,若点P,Q在运动到终点后继续在射线AB,BC上运动,直线AQ,CP交于点M,则∠QMC的大小变化吗?若变化,请说明理由;若不变,求出它的度数.
答案
一、1.B 2.A 3.B 4.D 5.A 6.C 7.C 8.B
9.D 10.C
二、11.5 12. 13.3
14.(1)70° (2)∠CFD=∠ABC
三、15.解:(1)如图,△DEF即为所作.
(2)由图可知,D(1,0),E(3,3),F(5,1).
16.证明:在△ABO和△DCO中,
∴△ABO≌△DCO,∴OB=OC,∴∠OBC=∠OCB.
四、17.证明:∵ED⊥AB,∴∠ADE=90°.
在Rt△ADE和Rt△ACE中,∵
∴Rt△ADE≌Rt△ACE,∴∠CAE=∠DAE.
在Rt△ACB中,∠CAE+∠DAE+∠B=90°,∠B=30°,∴∠CAE=∠DAE=∠B=30°,∴EA=EB.
∵ED⊥AB,∴AD=BD,即D为AB的中点.
18.(1)解:如图,射线AP即为所作.
(2)证明:如图,连接PD.
∵AP平分∠BAC,∴∠PAB=∠PAD.
又∵AB=AD,AP=AP,∴△PAB≌△PAD.
∴∠B=∠ADP.
∵∠B=2∠C,∠ADP=∠DPC+∠C,
∴2∠C=∠DPC+∠C,∴∠DPC=∠C,∴DP=DC,
∴点D在线段PC的垂直平分线上.
五、19.(1)证明:连接AE.∵AD⊥BC,且D为线段BE的中点,∴AD垂直平分线段BE,∴AB=AE.
∵EF垂直平分线段AC,∴AE=CE,∴AB=CE.
(2)解:∵AE=CE,∠C=32°,∴∠CAE=∠C=32°,
∴∠AEB=∠CAE+∠C=64°.
∵AB=AE,∴∠B=∠AEB=64°,
∴∠BAC=180°-∠B-∠C=84°.
20.(1)证明:如图,∵AD是∠BAC的平分线,
∴∠1=∠2.
∵EF∥AD,∴∠2=∠P,∠1=∠3.∴∠3=∠P.
∴AF=AP.∴△APF是等腰三角形.
(2)证明:如图,延长FE至点Q,使得EQ=EF,连接CQ.∵E为BC的中点,∴BE=CE.
又∵∠FEB=∠QEC,EF=EQ,
∴△EBF≌△ECQ,
∴∠BFE=∠Q,CQ=BF.
又∵∠BFE=∠3,∠3=∠P,
∴∠Q=∠P.∴CQ=CP,∴CP=BF.
(3)解:由(1)知,AP=AF,由(2)知,BF=CP,
∴AB=BF+AF=PC+AP=AC+AP+AP=AC+2AP.
∵AB=12,AC=8,∴12=8+2AP,∴PA=2.
六、21.解:(1)根据题意得∠BAC=90°-75°=15°,∠CBE=90°-60°=30°,
∴∠C=∠CBE-∠BAC=30°-15°=15°.
(2)没有触礁的危险,理由如下:
如图,过点C作CD⊥AB交AB的延长线于点D,
根据题意,得AB=30×(11-9)=60(n mile),
由(1)知,∠BAC=∠ACB,∴BC=AB=60 n mile,
∵∠CBD=30°,∴CD=BC=30 n mile.
∵25<30,∴若该船继续向东航行没有触礁的危险.
七、22.(1)DC
(2)解:DA=DC,
证明:如图①,过点D作DE⊥BA交BA的延长线于点E,DF⊥BC于点F,
∵BD平分∠EBF,DE⊥BA,DF⊥BC,∴DE=DF.
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C.又∵∠E=∠DFC=90°,
∴△DEA≌△DFC,∴DA=DC.
(3)证明:如图②,在BC上截取BG=BD,连接DG,
∵AB=AC,∠A=100°,∴∠ABC=∠C=40°.
∵BD平分∠ABC,∴∠DBG=∠ABC=20°.
∵BD=BG,
∴∠BGD=∠BDG=80°,即∠A+∠BGD=180°,
由(2)的结论得AD=DG.
∵∠BGD=∠C+∠GDC,
∴∠GDC=∠C=40°,∴DG=CG,
∴AD=DG=CG,∴BD+AD=BG+CG=BC.
八、23.(1)证明:∵△ABC是等边三角形,
∴∠ABQ=∠CAP=60°,AB=CA.
又∵点P,Q的运动速度相同,∴AP=BQ.
在△ABQ与△CAP中,∵
∴△ABQ≌△CAP,∴AQ=CP.
(2)解:∠QMC的大小不变,为60°.
(3)解:∠QMC的大小不变.
同(1)可得,△ABQ≌△CAP,∴∠BAQ=∠ACP.
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM=∠ACP+∠APM=180°-∠PAC=180°-60°=120°.
一、选择题(本大题共10小题,每小题4分,满分40分)
题序 1 2 3 4 5 6 7 8 9 10
答案
1.端午节是中国传统节日,下列与端午节有关的文创图案中,成轴对称的是( )
2.若点M(2a,1)与点N(4,-b)关于x轴对称,则ab的值为( )
A.2 B.-1 C.-2 D.3
3.如图所示的是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三边的垂直平分线的交点
(第3题) (第4题)
4.如图,若△ABC与△A1B1C1关于直线MN对称,BB1交MN于点O,则下列说法不一定正确的是( )
A.AC=A1C1 B.BO=B1O
C.CC1⊥MN D.AB∥B1C1
5.下列尺规作图,能判断AD是△ABC边上的中线的是( )
,A) ,B) ,C) ,D)
6.如图是通过折纸制作五角星的过程,则下列结论错误的是( )
A.∠1=∠2 B.∠1=∠3 C.∠1=∠4 D.∠3=∠2
7.如图,△ABC是等边三角形,D是AC的中点,DE⊥BC,CE=3,则△ABC的周长为( )
A.12 B.24 C.36 D.48
(第7题) (第8题) (第9题)
8.如图,在四边形ABDC中,对角线AD平分∠BAC,∠ACD=138°,∠ACB+∠BCD=90°,则∠ADB的度数为( )
A.42° B.48° C.50° D.53°
9.如图,在△ABC中,AB=AC=13,AD=12,BC=10,AD平分∠BAC,E是线段AC上的动点,P是线段AD上的动点,则PC+PE的最小值为( )
A. B. C. D.
10.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,F是CB延长线上一点,AF⊥CF,垂足为F,下列结论:①BC=DE;②AF=CF;③四边形ABCD的面积等于AC2;④S△BCD=S△ABF+S△ADE,其中正确的是( )
A.①② B.②③ C.①②③ D.①②③④
(第10题) (第11题) (第12题)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图所示的图形为轴对称图形,该图形的对称轴的条数为__________.
12.如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=4,BC=5,S△ABC=6,则DE的长为______.
13.如图,CD是等边三角形ABC边AB上的中线,AC的垂直平分线交AC于点E,交CD于点F.若DF=1,则CD的长为________.
(第13题) (第14题)
14.如图,在△ABC中,AB=BC,D是BC上一点,DE⊥AB于点E,DF⊥BC,交AC于点F,连接BF.
(1)若∠AFD=145°,则∠EDF=________;
(2)若F是AC的中点,则∠ABC与∠CFD之间的数量关系为______________.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,在平面直角坐标系中,网格上的每个小正方形的边长均为1,△ABC的顶点坐标分别为A(-1,0),B(-3,3),C(-5,1).
(1)在图中画出△ABC关于y轴对称的△DEF(点A,B,C的对应点分别为点D,E,F);
(2)在(1)的条件下,写出点D,E,F的坐标.
16.如图,已知AB=DC,∠A=∠D,AC与DB相交于点O,求证:∠OBC=∠OCB.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在Rt△ACB中,∠C=90°,∠B=30°,点E在BC上,作ED⊥AB于点D,且EC=ED.求证:D为AB的中点.
18.如图,已知在△ABC中,点D在边AC上,且AB=AD,∠B=2∠C.
(1)尺规作图:作∠BAC的平分线AP,交BC于点P;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:点D在线段PC的垂直平分线上.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在△ABC中,EF是AC的垂直平分线,AD⊥BC,D为线段BE的中点.
(1)求证:AB=CE;
(2)若∠C=32°,求∠BAC的度数.
20.如图,在△ABC中,AD是∠BAC的平分线,E是BC的中点,过点E作EF∥AD交CA的延长线于点P,交AB于点F.
(1)求证:△APF是等腰三角形;
(2)求证:BF=CP;
(3)若AB=12,AC=8,试求出PA的长.
六、(本题满分12分)
21.如图,灯塔C在海岛A 的北偏东75°的方向,某天9时,一艘船从海岛A 出发,以30 n mile/h的速度向东航行,11时到达 B 处,此时测得灯塔C在B 处的北偏东60°的方向.
(1)求∠C的度数;
(2)已知在以灯塔C为中心,周围25 n mile的范围内均有暗礁,若该船继续向东航行,是否有触礁的危险?请说明理由.
七、(本题满分12分)
22.我们定义:在四边形ABCD中,如果∠A=α(0°<α<180°),∠C=180°-α,对角线BD平分∠ABC,我们称这种四边形为“分角对补四边形”.
【特例感知】(1)如图①,当α=90°时,由角平分线的性质可得DA=__________;
【猜想论证】(2)如图②,当α为任意度数时,猜想DA与DC的数量关系,并给予证明;
【探究应用】(3)请利用(2)中的结论解决问题:如图③,在△ABC中,AB=AC,∠BAC=100°.BD平分∠ABC,求证:BD+AD=BC.
八、(本题满分14分)
23.如图①,已知等边三角形ABC,P,Q分别是边AB,BC上的动点(端点除外),点P,Q分别从顶点A,B同时出发,向点B,C运动,且它们的运动速度相同,AQ,CP交于点M.
(1)求证:AQ=CP;
(2)当点P,Q分别在AB,BC边上运动时,∠QMC的大小变化吗?若变化,请说明理由;若不变,请直接写出它的度数;
(3)如图②,若点P,Q在运动到终点后继续在射线AB,BC上运动,直线AQ,CP交于点M,则∠QMC的大小变化吗?若变化,请说明理由;若不变,求出它的度数.
答案
一、1.B 2.A 3.B 4.D 5.A 6.C 7.C 8.B
9.D 10.C
二、11.5 12. 13.3
14.(1)70° (2)∠CFD=∠ABC
三、15.解:(1)如图,△DEF即为所作.
(2)由图可知,D(1,0),E(3,3),F(5,1).
16.证明:在△ABO和△DCO中,
∴△ABO≌△DCO,∴OB=OC,∴∠OBC=∠OCB.
四、17.证明:∵ED⊥AB,∴∠ADE=90°.
在Rt△ADE和Rt△ACE中,∵
∴Rt△ADE≌Rt△ACE,∴∠CAE=∠DAE.
在Rt△ACB中,∠CAE+∠DAE+∠B=90°,∠B=30°,∴∠CAE=∠DAE=∠B=30°,∴EA=EB.
∵ED⊥AB,∴AD=BD,即D为AB的中点.
18.(1)解:如图,射线AP即为所作.
(2)证明:如图,连接PD.
∵AP平分∠BAC,∴∠PAB=∠PAD.
又∵AB=AD,AP=AP,∴△PAB≌△PAD.
∴∠B=∠ADP.
∵∠B=2∠C,∠ADP=∠DPC+∠C,
∴2∠C=∠DPC+∠C,∴∠DPC=∠C,∴DP=DC,
∴点D在线段PC的垂直平分线上.
五、19.(1)证明:连接AE.∵AD⊥BC,且D为线段BE的中点,∴AD垂直平分线段BE,∴AB=AE.
∵EF垂直平分线段AC,∴AE=CE,∴AB=CE.
(2)解:∵AE=CE,∠C=32°,∴∠CAE=∠C=32°,
∴∠AEB=∠CAE+∠C=64°.
∵AB=AE,∴∠B=∠AEB=64°,
∴∠BAC=180°-∠B-∠C=84°.
20.(1)证明:如图,∵AD是∠BAC的平分线,
∴∠1=∠2.
∵EF∥AD,∴∠2=∠P,∠1=∠3.∴∠3=∠P.
∴AF=AP.∴△APF是等腰三角形.
(2)证明:如图,延长FE至点Q,使得EQ=EF,连接CQ.∵E为BC的中点,∴BE=CE.
又∵∠FEB=∠QEC,EF=EQ,
∴△EBF≌△ECQ,
∴∠BFE=∠Q,CQ=BF.
又∵∠BFE=∠3,∠3=∠P,
∴∠Q=∠P.∴CQ=CP,∴CP=BF.
(3)解:由(1)知,AP=AF,由(2)知,BF=CP,
∴AB=BF+AF=PC+AP=AC+AP+AP=AC+2AP.
∵AB=12,AC=8,∴12=8+2AP,∴PA=2.
六、21.解:(1)根据题意得∠BAC=90°-75°=15°,∠CBE=90°-60°=30°,
∴∠C=∠CBE-∠BAC=30°-15°=15°.
(2)没有触礁的危险,理由如下:
如图,过点C作CD⊥AB交AB的延长线于点D,
根据题意,得AB=30×(11-9)=60(n mile),
由(1)知,∠BAC=∠ACB,∴BC=AB=60 n mile,
∵∠CBD=30°,∴CD=BC=30 n mile.
∵25<30,∴若该船继续向东航行没有触礁的危险.
七、22.(1)DC
(2)解:DA=DC,
证明:如图①,过点D作DE⊥BA交BA的延长线于点E,DF⊥BC于点F,
∵BD平分∠EBF,DE⊥BA,DF⊥BC,∴DE=DF.
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C.又∵∠E=∠DFC=90°,
∴△DEA≌△DFC,∴DA=DC.
(3)证明:如图②,在BC上截取BG=BD,连接DG,
∵AB=AC,∠A=100°,∴∠ABC=∠C=40°.
∵BD平分∠ABC,∴∠DBG=∠ABC=20°.
∵BD=BG,
∴∠BGD=∠BDG=80°,即∠A+∠BGD=180°,
由(2)的结论得AD=DG.
∵∠BGD=∠C+∠GDC,
∴∠GDC=∠C=40°,∴DG=CG,
∴AD=DG=CG,∴BD+AD=BG+CG=BC.
八、23.(1)证明:∵△ABC是等边三角形,
∴∠ABQ=∠CAP=60°,AB=CA.
又∵点P,Q的运动速度相同,∴AP=BQ.
在△ABQ与△CAP中,∵
∴△ABQ≌△CAP,∴AQ=CP.
(2)解:∠QMC的大小不变,为60°.
(3)解:∠QMC的大小不变.
同(1)可得,△ABQ≌△CAP,∴∠BAQ=∠ACP.
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM=∠ACP+∠APM=180°-∠PAC=180°-60°=120°.
