第一章 抛体运动 复习提升(含答案解析)
文档属性
| 名称 | 第一章 抛体运动 复习提升(含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-12-04 16:20:58 | ||
图片预览


文档简介
第一章 抛体运动
本章复习提升
易混易错练
易错点1 混淆参考系导致轨迹判断出错
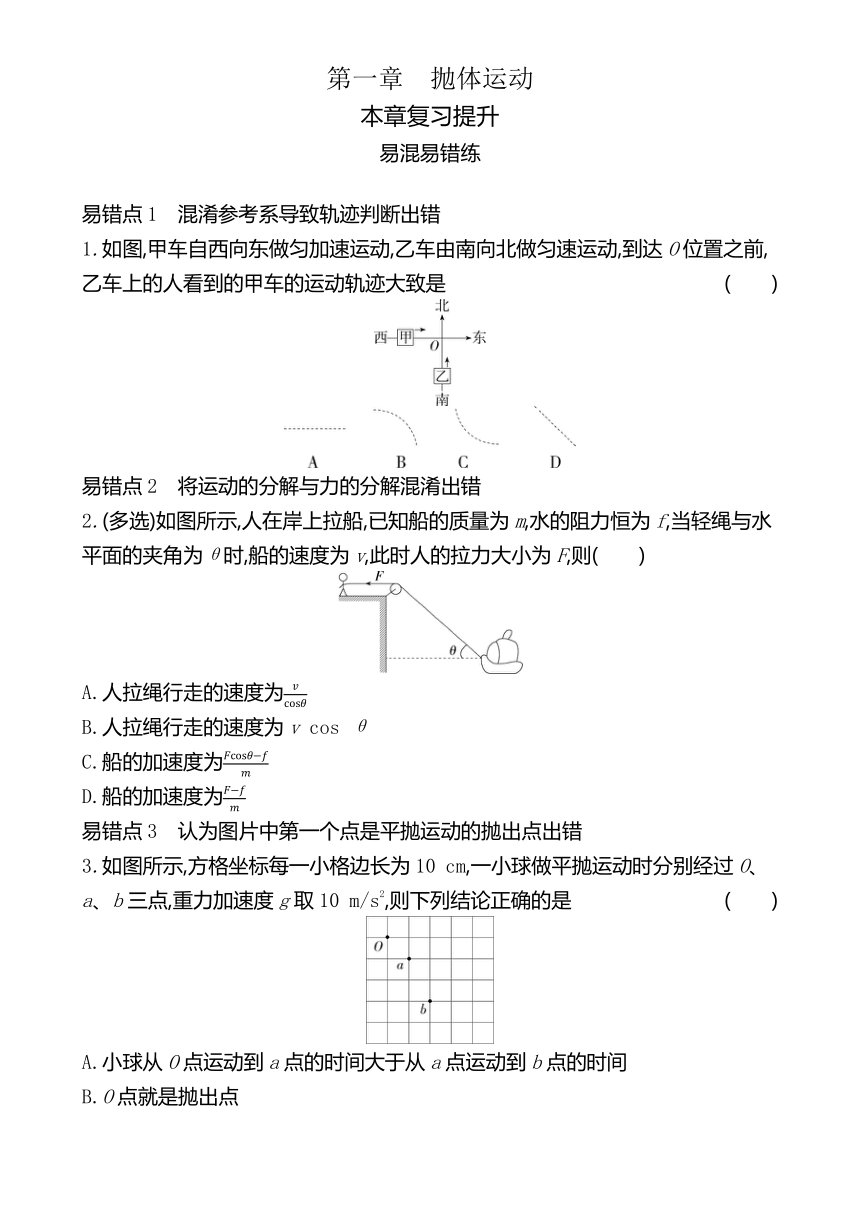
1.如图,甲车自西向东做匀加速运动,乙车由南向北做匀速运动,到达O位置之前,乙车上的人看到的甲车的运动轨迹大致是 ( )
易错点2 将运动的分解与力的分解混淆出错
2.(多选)如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
A.人拉绳行走的速度为
B.人拉绳行走的速度为v cos θ
C.船的加速度为
D.船的加速度为
易错点3 认为图片中第一个点是平抛运动的抛出点出错
3.如图所示,方格坐标每一小格边长为10 cm,一小球做平抛运动时分别经过O、a、b三点,重力加速度g取10 m/s2,则下列结论正确的是 ( )
A.小球从O点运动到a点的时间大于从a点运动到b点的时间
B.O点就是抛出点
C.小球抛出速度为1 m/s
D.以上说法均错误
易错点4 寻找临界条件出错
4.如图所示,长、宽、高分别为2L、L、h的长方体盒子固定在水平地面上,M为盒子右侧底边中点,O为地面上一点,OM长为L,且与盒子右侧底边垂直,一小球(可视为质点)从O点正上方3h处水平抛出,不计空气阻力,若抛出的速度大小和方向合适,小球不和盒子侧壁接触直接落在盒子底面上,则小球初速度的取值范围为( )
A.LB.LC.LD.L
一、正交分解法
方法概述
将复杂的曲线运动分解为两个互相垂直方向上的直线运动的方法是正交分解法,一般水平方向为x轴,竖直方向为y轴。与斜面相关的平抛运动问题、求距斜面的最大距离时,常将重力加速度分解到垂直斜面和平行斜面方向上。
1.质量不同的甲、乙两个小球在同一位置分别以v1、v2的水平初速度向一倾角为θ的斜面抛出,飞行一段时间后,甲球恰好垂直撞在斜面上,小球在空中的飞行时间为t1;乙球到达斜面的位移恰好最小,小球在空中的飞行时间为t2,则t1∶t2等于 ( )
A.2∶1 B.1∶2 C.2v2∶v1 D.v1∶2v2
二、逆向思维法
方法概述
逆向思维法是指把运动过程的“末态”当成“初态”来反向研究问题的方法。该方法一般用于末态已知的情况或末态很容易确定的情况。如匀减速直线运动可看成是加速度等大反向的匀加速运动过程、竖直上抛运动的上抛阶段可看成是自由落体运动的逆过程。
2.如图所示,某同学分别在同一直线上的A、B、C三个位置投掷篮球,结果都击中篮板,击中篮板时篮球的速度方向均水平,大小分别为v1、v2、v3,若篮球出手时高度相同,速度的方向与水平方向的夹角分别是θ1、θ2、θ3,不计空气阻力,则下列说法正确的是 ( )
A.v1v2>v3
C.θ1>θ2>θ3 D.θ1=θ2=θ3
三、对称法
方法概述
所谓对称法,实际上是根据某些物理现象、物理规律、物理过程或几何图形的对称性进行解题的一种方法,也称为镜像法。利用此方法分析解决问题可以避免复杂的数学演算和推导,直接抓住问题的实质,可以达到出奇制胜的效果。常见的应用有时间对称和空间对称等。
3.如图是某家用体育锻炼的发球机,从同一点沿不同方向发出A、B两球,返回同一水平面时,两球落至同一位置。如果不计空气阻力,关于两球的运动,下列说法正确的是 ( )
A.两球运动至最高点时,两球速度相等
B.两球运动过程中,A的加速度大于B的加速度
C.两球飞行时间相等
D.从抛出至落回同一水平面,A球速度变化量大于B球速度变化量
答案与分层梯度式解析
第一章 抛体运动
本章复习提升
易混易错练
1.C 以乙车为参考系,甲车在东西方向上做匀加速直线运动,在南北方向上做匀速直线运动,由于加速度的方向与合速度的方向不在同一条直线上,可知是曲线运动,加速度的方向大致指向轨迹凹侧,故C正确,A、B、D错误。
错解分析
混淆参考系,误以地面为参考系而得出错误答案,乙车上的人看到的甲车的运动轨迹,应以乙车为参考系。
2.BC 船运动的速度是合速度,根据平行四边形定则,有v人=v绳=v cos θ,A错误,B正确;对船受力分析,则有F cos θ-f=ma,因此船的加速度大小为a=,C正确,D错误。
错解分析
混淆力的分解和运动的分解,将绳的速度沿船前进方向和垂直于船前进方向分解,从而错选答案。当绳(杆)拉物体或物体拉绳(杆),以及两物体通过绳(杆)相连,物体运动方向与绳(杆)不在一条直线上时,物体的实际运动速度是合速度,沿绳(或杆)的速度是分速度,与绳(或杆)垂直的速度是分速度。
3.C 平抛运动的水平分运动为匀速直线运动,xOa=xab=L,运动时间t=,故tOa=tab,选项A错误;若O点为抛出点,则在竖直方向连续相等时间内通过的位移之比为1∶3∶5∶…,由题图可知,竖直方向连续相等时间内位移之比为1∶2,所以O点不是抛出点,选项B错误;根据匀变速直线运动规律Δy=aT2,a=g=10 m/s2,得T==0.1 s,即tOa=tab=T=0.1 s,小球抛出时的速度v==1 m/s,选项C正确,D错误。
错解分析
从图中可以看出O点是第一个点,即认为O点是抛出点,从而错选B。判断某点是不是抛出点,不能根据点迹排列的先后,要注意题目所给的平抛运动的轨迹图像,不一定是一个完整的图像,因此所标的第一个点不一定是抛出点,做题时一定要多加注意。
4.A 小球做平抛运动,由3h=gt2可知,小球从抛出至落在盒子底面的运动时间t=,当小球落在盒子左侧的两个角上时,小球的水平位移x==L,小球的初速度最大,最大初速度vmax==L。当小球恰好垂直擦过盒子右侧侧壁上边沿中点进入盒内时,小球的初速度最小,小球从抛出至垂直擦过盒子右侧侧壁的水平位移x'=L,竖直位移y=2h,由2h=gt'2,L=vmint',解得最小初速度vmin=L,所以小球不和盒子侧壁接触直接落在盒子底面上的初速度的取值范围为L错解分析
误认为射入与M正对的左侧壁对应点时速度最大,得3h=g,2L=v2t2得最大速度vmax=L,而误选B。解答此类问题时要做好临界条件分析,当受水平位移限制时,其临界轨迹为自抛出点到水平位移端点的一条抛物线;当受高度限制时,其临界轨迹为自抛出点到高度端点的一条抛物线。确定轨迹后再结合平抛运动遵循的运动规律即可求解。
思想方法练
1.D 将甲球垂直撞在斜面上的速度分解,如图甲所示,由图可知,则tan θ==,可得t1=。过乙球抛出点作斜面的垂线,如图乙所示,当小球落在斜面上的B点时,位移最小,则水平方向x=v2t2,竖直方向y=g,根据几何关系=tan θ,则=tan θ,解得t2=,则t1∶t2=v1∶2v2,选项D正确,A、B、C错误。
方法点津
小球垂直撞在斜面上时,应分解速度。小球到达斜面的位移最小时,应分解位移。在分解速度和分解位移时应采用正交分解法。利用正交分解法解题比较直观,当遇到位移、速度等物理量要求解分量时一般采用正交分解法。
2.B 三个篮球都垂直击中篮板,它们运动的逆过程是平抛运动,设任一篮球击中篮板的速度为v,上升的高度为h,水平位移为x,则有x=vt,h=gt2,解得v=x,由于h相同,xA>xB>xC,则v1>v2>v3,选项A错误,B正确;根据速度的分解有tan θ==,t相同,v1>v2>v3,则θ1<θ2<θ3 ,选项C、D错误。
方法点津
击中篮板时篮球的速度方向沿水平方向,采用逆向思维,篮球做反方向的平抛运动,根据平抛运动规律,求得篮球击中篮板时的速度大小v与水平位移x、竖直位移h的关系式,比较h、x的大小关系就可以得到速度v的大小关系。逆向思维法多适用于竖直上抛运动、匀减速直线运动、斜抛运动等中。
3.D 小球在竖直方向做竖直上抛运动,根据对称性可知其上升和下降的时间相等,其从最高点至落地过程中竖直方向为自由落体运动,由h=gt2,得t=,则运动的总时间为t总=2t=2,由此可知小球A在空中运动的时间大于小球B在空中运动的时间,选项C错误;由于两小球都做斜抛运动,水平方向都是匀速直线运动,运动到最高点时只有水平方向的速度,由于两球的水平位移相等,由x=vt可知,两球运动至最高点时小球A的速度小于小球B的速度,选项A错误;两球运动过程中都只受重力作用,加速度都是重力加速度g,选项B错误;根据速度变化量Δv=gΔt,由于小球A在空中运动的时间大于小球B在空中运动的时间,所以从抛出至落回同一水平面过程中,A球速度变化量大于B球速度变化量,选项D正确。
方法点津
本题体现了时间对称性的应用。解答本题时要明确小球的运动在竖直方向上是竖直上抛运动,在水平方向是匀速直线运动,先分析判断经过同一点的时间关系,再判断竖直方向和水平方向的速度大小关系,进而判断合速度大小关系。此方法多适用于竖直上抛运动、斜抛运动等。
本章复习提升
易混易错练
易错点1 混淆参考系导致轨迹判断出错
1.如图,甲车自西向东做匀加速运动,乙车由南向北做匀速运动,到达O位置之前,乙车上的人看到的甲车的运动轨迹大致是 ( )
易错点2 将运动的分解与力的分解混淆出错
2.(多选)如图所示,人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为F,则( )
A.人拉绳行走的速度为
B.人拉绳行走的速度为v cos θ
C.船的加速度为
D.船的加速度为
易错点3 认为图片中第一个点是平抛运动的抛出点出错
3.如图所示,方格坐标每一小格边长为10 cm,一小球做平抛运动时分别经过O、a、b三点,重力加速度g取10 m/s2,则下列结论正确的是 ( )
A.小球从O点运动到a点的时间大于从a点运动到b点的时间
B.O点就是抛出点
C.小球抛出速度为1 m/s
D.以上说法均错误
易错点4 寻找临界条件出错
4.如图所示,长、宽、高分别为2L、L、h的长方体盒子固定在水平地面上,M为盒子右侧底边中点,O为地面上一点,OM长为L,且与盒子右侧底边垂直,一小球(可视为质点)从O点正上方3h处水平抛出,不计空气阻力,若抛出的速度大小和方向合适,小球不和盒子侧壁接触直接落在盒子底面上,则小球初速度的取值范围为( )
A.L
一、正交分解法
方法概述
将复杂的曲线运动分解为两个互相垂直方向上的直线运动的方法是正交分解法,一般水平方向为x轴,竖直方向为y轴。与斜面相关的平抛运动问题、求距斜面的最大距离时,常将重力加速度分解到垂直斜面和平行斜面方向上。
1.质量不同的甲、乙两个小球在同一位置分别以v1、v2的水平初速度向一倾角为θ的斜面抛出,飞行一段时间后,甲球恰好垂直撞在斜面上,小球在空中的飞行时间为t1;乙球到达斜面的位移恰好最小,小球在空中的飞行时间为t2,则t1∶t2等于 ( )
A.2∶1 B.1∶2 C.2v2∶v1 D.v1∶2v2
二、逆向思维法
方法概述
逆向思维法是指把运动过程的“末态”当成“初态”来反向研究问题的方法。该方法一般用于末态已知的情况或末态很容易确定的情况。如匀减速直线运动可看成是加速度等大反向的匀加速运动过程、竖直上抛运动的上抛阶段可看成是自由落体运动的逆过程。
2.如图所示,某同学分别在同一直线上的A、B、C三个位置投掷篮球,结果都击中篮板,击中篮板时篮球的速度方向均水平,大小分别为v1、v2、v3,若篮球出手时高度相同,速度的方向与水平方向的夹角分别是θ1、θ2、θ3,不计空气阻力,则下列说法正确的是 ( )
A.v1
C.θ1>θ2>θ3 D.θ1=θ2=θ3
三、对称法
方法概述
所谓对称法,实际上是根据某些物理现象、物理规律、物理过程或几何图形的对称性进行解题的一种方法,也称为镜像法。利用此方法分析解决问题可以避免复杂的数学演算和推导,直接抓住问题的实质,可以达到出奇制胜的效果。常见的应用有时间对称和空间对称等。
3.如图是某家用体育锻炼的发球机,从同一点沿不同方向发出A、B两球,返回同一水平面时,两球落至同一位置。如果不计空气阻力,关于两球的运动,下列说法正确的是 ( )
A.两球运动至最高点时,两球速度相等
B.两球运动过程中,A的加速度大于B的加速度
C.两球飞行时间相等
D.从抛出至落回同一水平面,A球速度变化量大于B球速度变化量
答案与分层梯度式解析
第一章 抛体运动
本章复习提升
易混易错练
1.C 以乙车为参考系,甲车在东西方向上做匀加速直线运动,在南北方向上做匀速直线运动,由于加速度的方向与合速度的方向不在同一条直线上,可知是曲线运动,加速度的方向大致指向轨迹凹侧,故C正确,A、B、D错误。
错解分析
混淆参考系,误以地面为参考系而得出错误答案,乙车上的人看到的甲车的运动轨迹,应以乙车为参考系。
2.BC 船运动的速度是合速度,根据平行四边形定则,有v人=v绳=v cos θ,A错误,B正确;对船受力分析,则有F cos θ-f=ma,因此船的加速度大小为a=,C正确,D错误。
错解分析
混淆力的分解和运动的分解,将绳的速度沿船前进方向和垂直于船前进方向分解,从而错选答案。当绳(杆)拉物体或物体拉绳(杆),以及两物体通过绳(杆)相连,物体运动方向与绳(杆)不在一条直线上时,物体的实际运动速度是合速度,沿绳(或杆)的速度是分速度,与绳(或杆)垂直的速度是分速度。
3.C 平抛运动的水平分运动为匀速直线运动,xOa=xab=L,运动时间t=,故tOa=tab,选项A错误;若O点为抛出点,则在竖直方向连续相等时间内通过的位移之比为1∶3∶5∶…,由题图可知,竖直方向连续相等时间内位移之比为1∶2,所以O点不是抛出点,选项B错误;根据匀变速直线运动规律Δy=aT2,a=g=10 m/s2,得T==0.1 s,即tOa=tab=T=0.1 s,小球抛出时的速度v==1 m/s,选项C正确,D错误。
错解分析
从图中可以看出O点是第一个点,即认为O点是抛出点,从而错选B。判断某点是不是抛出点,不能根据点迹排列的先后,要注意题目所给的平抛运动的轨迹图像,不一定是一个完整的图像,因此所标的第一个点不一定是抛出点,做题时一定要多加注意。
4.A 小球做平抛运动,由3h=gt2可知,小球从抛出至落在盒子底面的运动时间t=,当小球落在盒子左侧的两个角上时,小球的水平位移x==L,小球的初速度最大,最大初速度vmax==L。当小球恰好垂直擦过盒子右侧侧壁上边沿中点进入盒内时,小球的初速度最小,小球从抛出至垂直擦过盒子右侧侧壁的水平位移x'=L,竖直位移y=2h,由2h=gt'2,L=vmint',解得最小初速度vmin=L,所以小球不和盒子侧壁接触直接落在盒子底面上的初速度的取值范围为L
误认为射入与M正对的左侧壁对应点时速度最大,得3h=g,2L=v2t2得最大速度vmax=L,而误选B。解答此类问题时要做好临界条件分析,当受水平位移限制时,其临界轨迹为自抛出点到水平位移端点的一条抛物线;当受高度限制时,其临界轨迹为自抛出点到高度端点的一条抛物线。确定轨迹后再结合平抛运动遵循的运动规律即可求解。
思想方法练
1.D 将甲球垂直撞在斜面上的速度分解,如图甲所示,由图可知,则tan θ==,可得t1=。过乙球抛出点作斜面的垂线,如图乙所示,当小球落在斜面上的B点时,位移最小,则水平方向x=v2t2,竖直方向y=g,根据几何关系=tan θ,则=tan θ,解得t2=,则t1∶t2=v1∶2v2,选项D正确,A、B、C错误。
方法点津
小球垂直撞在斜面上时,应分解速度。小球到达斜面的位移最小时,应分解位移。在分解速度和分解位移时应采用正交分解法。利用正交分解法解题比较直观,当遇到位移、速度等物理量要求解分量时一般采用正交分解法。
2.B 三个篮球都垂直击中篮板,它们运动的逆过程是平抛运动,设任一篮球击中篮板的速度为v,上升的高度为h,水平位移为x,则有x=vt,h=gt2,解得v=x,由于h相同,xA>xB>xC,则v1>v2>v3,选项A错误,B正确;根据速度的分解有tan θ==,t相同,v1>v2>v3,则θ1<θ2<θ3 ,选项C、D错误。
方法点津
击中篮板时篮球的速度方向沿水平方向,采用逆向思维,篮球做反方向的平抛运动,根据平抛运动规律,求得篮球击中篮板时的速度大小v与水平位移x、竖直位移h的关系式,比较h、x的大小关系就可以得到速度v的大小关系。逆向思维法多适用于竖直上抛运动、匀减速直线运动、斜抛运动等中。
3.D 小球在竖直方向做竖直上抛运动,根据对称性可知其上升和下降的时间相等,其从最高点至落地过程中竖直方向为自由落体运动,由h=gt2,得t=,则运动的总时间为t总=2t=2,由此可知小球A在空中运动的时间大于小球B在空中运动的时间,选项C错误;由于两小球都做斜抛运动,水平方向都是匀速直线运动,运动到最高点时只有水平方向的速度,由于两球的水平位移相等,由x=vt可知,两球运动至最高点时小球A的速度小于小球B的速度,选项A错误;两球运动过程中都只受重力作用,加速度都是重力加速度g,选项B错误;根据速度变化量Δv=gΔt,由于小球A在空中运动的时间大于小球B在空中运动的时间,所以从抛出至落回同一水平面过程中,A球速度变化量大于B球速度变化量,选项D正确。
方法点津
本题体现了时间对称性的应用。解答本题时要明确小球的运动在竖直方向上是竖直上抛运动,在水平方向是匀速直线运动,先分析判断经过同一点的时间关系,再判断竖直方向和水平方向的速度大小关系,进而判断合速度大小关系。此方法多适用于竖直上抛运动、斜抛运动等。
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
