第三章 万有引力定律 综合拔高练(含答案解析)
文档属性
| 名称 | 第三章 万有引力定律 综合拔高练(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-12-04 00:00:00 | ||
图片预览




文档简介
第三章 万有引力定律
综合拔高练
五年高考练
考点1 万有引力定律及其应用
1.(2022广东,2)“祝融号”火星车需要“休眠”以度过火星寒冷的冬季。假设火星和地球的冬季是各自公转周期的四分之一,且火星的冬季时长约为地球的1.88倍。火星和地球绕太阳的公转均可视为匀速圆周运动。下列关于火星、地球公转的说法正确的是 ( )
A.火星公转的线速度比地球的大
B.火星公转的角速度比地球的大
C.火星公转的半径比地球的小
D.火星公转的加速度比地球的小
2.(2022全国乙,14)2022年3月,中国航天员翟志刚、王亚平、叶光富在离地球表面约400 km的“天宫二号”空间站上通过天地连线,为同学们上了一堂精彩的科学课。通过直播画面可以看到,在近地圆轨道上飞行的“天宫二号”中,航天员可以自由地漂浮,这表明他们( )
A.所受地球引力的大小近似为零
B.所受地球引力与飞船对其作用力两者的合力近似为零
C.所受地球引力的大小与其随飞船运动所需向心力的大小近似相等
D.在地球表面上所受引力的大小小于其随飞船运动所需向心力的大小
3.(2021广东,2)2021年4月,我国自主研发的空间站“天和”核心舱成功发射并入轨运行。若核心舱绕地球的运行可视为匀速圆周运动,已知引力常量,由下列物理量能计算出地球质量的是 ( )
A.核心舱的质量和绕地半径
B.核心舱的质量和绕地周期
C.核心舱的绕地角速度和绕地周期
D.核心舱的绕地线速度和绕地半径
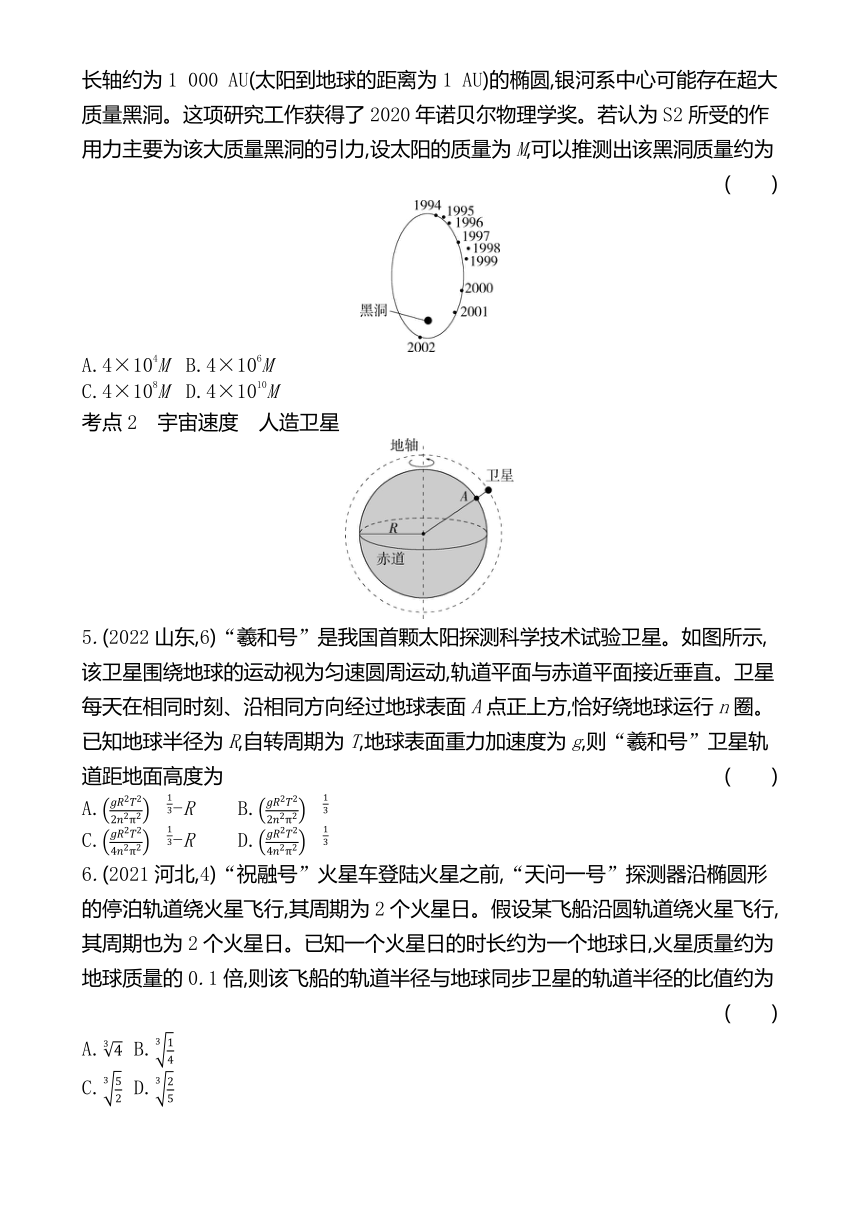
4.(2021全国乙,18)科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示。科学家认为S2的运动轨迹是半长轴约为1 000 AU(太阳到地球的距离为1 AU)的椭圆,银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M,可以推测出该黑洞质量约为 ( )
A.4×104M B.4×106M
C.4×108M D.4×1010M
考点2 宇宙速度 人造卫星
5.(2022山东,6)“羲和号”是我国首颗太阳探测科学技术试验卫星。如图所示,该卫星围绕地球的运动视为匀速圆周运动,轨道平面与赤道平面接近垂直。卫星每天在相同时刻、沿相同方向经过地球表面A点正上方,恰好绕地球运行n圈。已知地球半径为R,自转周期为T,地球表面重力加速度为g,则“羲和号”卫星轨道距地面高度为 ( )
A.-R B.
C.-R D.
6.(2021河北,4)“祝融号”火星车登陆火星之前,“天问一号”探测器沿椭圆形的停泊轨道绕火星飞行,其周期为2个火星日。假设某飞船沿圆轨道绕火星飞行,其周期也为2个火星日。已知一个火星日的时长约为一个地球日,火星质量约为地球质量的0.1倍,则该飞船的轨道半径与地球同步卫星的轨道半径的比值约为 ( )
A. B.
C. D.
7.(2021全国甲,18)2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入运行周期约为1.8×105 s的椭圆形停泊轨道,轨道与火星表面的最近距离约为2.8×105 m。已知火星半径约为3.4×106 m,火星表面处自由落体的加速度大小约为3.7 m/s2,则“天问一号”的停泊轨道与火星表面的最远距离约为 ( )
A.6×105 m B.6×106 m
C.6×107 m D.6×108 m
8.(2021湖南,7)(多选)2021年4月29日,中国空间站天和核心舱发射升空,准确进入预定轨道。根据任务安排,后续将发射问天实验舱和梦天实验舱,计划2022年完成空间站在轨建造。核心舱绕地球飞行的轨道可视为圆轨道,轨道离地面的高度约为地球半径的 。下列说法正确的是 ( )
A.核心舱进入轨道后所受地球的万有引力大小约为它在地面时的倍
B.核心舱在轨道上飞行的速度大于7.9 km/s
C.核心舱在轨道上飞行的周期小于24 h
D.后续加挂实验舱后,空间站由于质量增大,轨道半径将变小
9.(2020课标Ⅲ,16)“嫦娥四号”探测器于2019年1月在月球背面成功着陆,着陆前曾绕月球飞行,某段时间可认为绕月做匀速圆周运动,圆周半径为月球半径的K倍。已知地球半径R是月球半径的P倍,地球质量是月球质量的Q倍,地球表面重力加速度大小为g。则“嫦娥四号”绕月球做圆周运动的速率为 ( )
A. B.
C. D.
10.(2020江苏单科,7)(多选)甲、乙两颗人造卫星质量相等,均绕地球做圆周运动,甲的轨道半径是乙的2倍。下列应用公式进行的推论正确的有 ( )
A.由v=可知,甲的速度是乙的倍
B.由a=ω2r可知,甲的向心加速度是乙的2倍
C.由F=G可知,甲的向心力是乙的
D.由=k可知,甲的周期是乙的2倍
11.(2022湖南,8)(多选)如图,火星与地球近似在同一平面内,绕太阳沿同一方向做匀速圆周运动,火星的轨道半径大约是地球的1.5倍。地球上的观测者在大多数的时间内观测到火星相对于恒星背景由西向东运动,称为顺行;有时观测到火星由东向西运动,称为逆行。当火星、地球、太阳三者在同一直线上,且太阳和火星位于地球两侧时,称为火星冲日。忽略地球自转,只考虑太阳对行星的引力,下列说法正确的是 ( )
A.火星的公转周期大约是地球的倍
B.在冲日处,地球上的观测者观测到火星的运动为顺行
C.在冲日处,地球上的观测者观测到火星的运动为逆行
D.在冲日处,火星相对于地球的速度最小
12.(2021重庆,8)(多选)2021年5月15日“祝融号”火星车成功着陆火星表面,是我国航天事业发展中具有里程碑意义的进展。此前我国“玉兔二号”月球车首次实现月球背面软着陆,若“祝融号”的质量是“玉兔二号”的K倍,火星的质量是月球的N倍,火星的半径是月球的P倍,火星与月球均视为球体,则 ( )
A.火星的平均密度是月球的倍
B.火星的第一宇宙速度是月球的倍
C.火星的重力加速度大小是月球表面的倍
D.火星对“祝融号”引力的大小是月球对“玉兔二号”引力的倍
13.(2021辽宁,8)2021年2月,我国首个火星探测器“天问一号”实现了对火星的环绕。若已知该探测器在近火星圆轨道与在近地球圆轨道运行的速率比和周期比,则可求出火星与地球的 ( )
A.半径比 B.质量比
C.自转角速度比 D.公转轨道半径比
14.(2021福建,13)一火星探测器着陆火星之前,需经历动力减速、悬停避障两个阶段。在动力减速阶段,探测器速度大小由96 m/s减小到0,历时80 s。在悬停避障阶段,探测器启用最大推力为7 500 N的变推力发动机,在距火星表面约百米高度处悬停,寻找着陆点。已知火星半径约为地球半径的,火星质量约为地球质量的,地球表面重力加速度大小取10 m/s2,探测器在动力减速阶段的运动视为竖直向下的匀减速运动。求:
(1)在动力减速阶段,探测器的加速度大小和下降距离;
(2)在悬停避障阶段,能借助该变推力发动机实现悬停的探测器的最大质量。
高考模拟练
应用实践
1.如图为“天问一号”探测器进入火星停泊轨道(椭圆轨道)。若火星可视为半径为R质量均匀分布的球体,轨道的近火点P到火星表面的距离为L1,远火点Q到火星表面的距离为L2,已知探测器在轨道上运行的周期为T,L1+L2≈18R,引力常量为G。则火星的密度约为 ( )
A. B.
C. D.
2.如图是北斗卫星导航系统中三个卫星的圆轨道示意图,其中A为地球赤道同步轨道;轨道B为倾斜同步轨道,轨道半径与地球赤道同步轨道半径相同;轨道C为中圆地球轨道。则下列说法中正确的是 ( )
A.在轨道A、B、C上运动的卫星的线速度大小关系为vA=vB>vC
B.在轨道A、B上运动的卫星需要的向心力大小一定相等
C.在轨道A、C上运动的卫星周期关系为TAD.在轨道A、B、C上运动的卫星周期的平方和轨道半径三次方的比值相等
3.在人类太空征服史中,让人类遗憾的是“太空加油站”的缺乏。当通信卫星轨道校正能源耗尽的时候,它的生命就走到了尽头,有很多成了太空垃圾。如今“轨道康复者”是救助此类卫星的新型太空航天器,图甲是“轨道康复者”航天器在给太空中“垃圾”卫星补充能源,可简化为图乙所示的模型。下列说法正确的是 ( )
A.“轨道康复者”N从图乙所示轨道上加速,与卫星M对接补充能源后开启M上的小发动机向前喷气,能校正卫星M到较低的轨道运行
B.让M降低到N所在轨道上,补充能源后再开启卫星M上的小发动机向前喷气末进行校正
C.在图乙中M的线速度一定大于N的线速度
D.在图乙中,M、N和地球球心三者不可能处在同一直线上
4.(多选)如图所示是卫星绕行星沿不同轨道运动的lg T-lg r图像,其中T为卫星的周期,r为卫星的轨道半径。卫星M绕行星P运动的图线是a,卫星N绕行星Q运动的图线是b,若卫星绕行星的运动可以看成匀速圆周运动,则 ( )
A.卫星M在点1对应的角速度小于在点2对应的角速度
B.卫星M在点2对应的线速度小于卫星N在点3对应的线速度
C.直线的斜率与行星质量无关
D.行星P的质量大于行星Q的质量
5.如图甲所示,河外星系中两黑洞A、B的质量分别为M1和M2,它们以两者连线上的某一点为圆心做匀速圆周运动。为研究方便简化为如图乙所示示意图,黑洞A和黑洞B均可看成球体,OA>OB,且黑洞A的半径大于黑洞B的半径。根据你所学知识,下列说法正确的是 ( )
A.两黑洞质量之间的关系一定是M1>M2
B.黑洞A的运行角速度小于黑洞B的运行角速度
C.若两黑洞间的距离一定,把黑洞A上的物质移到黑洞B上,则它们间的万有引力会变大
D.人类要把宇航器发射到距黑洞A较近的区域进行探索,发射速度一定大于第三宇宙速度
迁移创新
6.已知地球质量为M,引力常量为G。将地球视为半径为R、质量均匀分布的球体。在以下问题的讨论中,空气阻力及地球自转的影响均忽略不计。
(1)物体在地面附近绕地球做匀速圆周运动的速度,叫作第一宇宙速度。请证明第一宇宙速度的大小v1=。
(2)某同学设想从地面以第一宇宙速度v1竖直上抛一可视为质点的物体,关于物体上升的最大高度,他的解答过程如下:
设物体的质量为m,上升的最大高度为h,重力加速度为g,由机械能守恒定律有m=mgh
又v1=,=mg,所以v1=
联立得h=。老师说该同学的上述解答是不正确的,请指出上述解答错误的原因,并分析说明物体上升的最大高度h应该比大还是小
(3)试分析说明第(2) 问中将物体以第一宇宙速度v1竖直上抛至物体落回抛出点的整个过程中,物体的速度和加速度的变化情况,并以竖直向上为正方向,在图中定性画出物体从抛出到落回抛出点的整个过程中速度随时间变化的v-t图像。
答案与分层梯度式解析
第三章 万有引力定律
综合拔高练
五年高考练
1.D 由题意可知T火=1.88T地,结合开普勒第三定律有=,整理可得=,可见r火>r地,故C错误;由=m,得v=,可见v火2.C 万有引力F=G,航天员受万有引力,且万有引力提供向心力,航天员所受合力不为零,地表处r较小,航天员在地表处所受万有引力大于在飞船上所受的万有引力,航天员在飞船上所受地球引力,约等于随飞船运动所需的向心力,所以A、B、D错误,C正确。
3.D 核心舱绕地球做匀速圆周运动,有==mω2r=mr,核心舱的质量在求地球质量时会被约掉,已知核心舱绕地线速度和半径或者绕地角速度和半径或者绕地周期和半径即可求出地球质量,则D正确。故选D项。
4.B 地球绕太阳做匀速圆周运动,太阳对地球的万有引力提供地球做圆周运动所需向心力,有=mr,化简得=M,由此推断S2绕黑洞做椭圆运动时,半长轴的三次方与周期二次方的比值与黑洞质量成正比,有=,由观测推算S2的周期约为16年,代入数据解得M黑≈4×106M,选B。
5.C 根据题意,卫星绕地球的周期t=,设地球质量为M,地心与卫星中心距离为r,卫星绕地球做匀速圆周运动,根据万有引力提供向心力可知=mr,则GM=r3,且GM=gR2,h=r-R,代入化简得h=-R,故选C。
6.D 由万有引力提供向心力得=m
解得r=
即飞船轨道半径r飞=
地球同步卫星轨道半径r同=
由题可知T飞=2T同,M火=0.1 M地
可得=,故选D。
7.C 设火星的质量为M,半径为R,自由落体的加速度为g火,则有=mg火,设其近地卫星做圆周运动的周期为T,则有=mR,设探测器所在椭圆形停泊轨道的半长轴为a,根据开普勒第三定律得=,联立上述方程并代入数据解得a≈×107 m,可得停泊轨道与火星表面的最远距离约为2a-2.8×105 m-2×3.4×106 m≈6×107 m,故选项C正确,选项A、B、D错误。故选C项。
8.AC 核心舱在地面上所受万有引力F0=G ,入轨后,所受万有引力F=G =F0,选项A正确;核心舱绕地球运行的最大速度为7.9 km/s,选项B错误;核心舱轨道半径小于地球同步卫星的轨道半径,其周期小于24 h,选项C正确;根据G =,可知r= ,空间站的轨道半径与其速度v有关,与其质量无关,选项D错误。
9.D 设月球质量为m、半径为r
则地球质量为Qm、半径R=Pr
探测器绕月运动半径为Kr=K· ①
地球表面重力加速度大小为g,则=m0g ②
探测器绕月运动,由牛顿第二定律得
=m' ③
由①②③式得v=,故D正确。
10.CD 由=mg可知,在离地不同高度处重力加速度不同,而A项推论误将g作为一个常量,故A项所得结果错误。同理由=mrω2可知卫星在不同轨道上运行的角速度不同,B项将ω作为常量做出的推论也是错误的。由万有引力定律可知C项正确。由=mr可得=,可见k=是一个只与地球质量有关的物理量,故D项由此所得推论是正确的。
11.CD 由开普勒第三定律有=,得==,A错误;由=m,得v=,故v火12.AD 由密度的定义有ρ=,体积V= πR3可知,火星的平均密度与月球的平均密度之比为=·=,即火星的平均密度是月球的倍,故A正确;根据G=mg可知,火星的重力加速度与月球表面的重力加速度之比为==,即火星的重力加速度是月球表面的重力加速度的,由G=mg,G=m,可知火星的第一宇宙速度与月球的第一宇宙速度之比为==,故B、C错误;根据万有引力定律F=G可知,火星对“祝融号”引力大小与月球对“玉兔二号”引力大小之比为=··=,即火星对“祝融号”引力大小是月球对“玉兔二号”引力大小的倍,故D正确。
13.AB 探测器绕火星和地球的运动均可视为匀速圆周运动。
根据v=
得r=
故=
故火星与地球的半径比可求,A正确;
以探测器为研究对象,环绕过程中万有引力提供向心力,有
G=
中心天体的质量M=
故=
故火星和地球的质量比可求,B正确;
火星与地球的公转轨道半径比和自转角速度比由于条件不足,无法求得,故C、D错误。
14.答案 (1)1.2 m/s2 3 840 m (2)1 875 kg
解析 (1)设探测器在动力减速阶段所用时间为t,初速度大小为v1,末速度大小为v2,加速度大小为a,由匀变速直线运动速度公式有
v2=v1-at ①
代入题给数据得
a=1.2 m/s2 ②
设探测器下降的距离为s,由匀变速直线运动位移公式有
s=v1t-at2 ③
联立②③式并代入题给数据得
s=3 840 m④
(2)设火星的质量、半径和表面重力加速度大小分别为M火、r火、g火,地球的质量、半径和表面重力加速度大小分别为M地、r地、g地。由牛顿运动定律和万有引力定律,对星球表面质量为m的物体有
=mg火 ⑤
=mg地 ⑥
式中G为引力常量。设变推力发动机的最大推力为F,能够悬停的火星探测器最大质量为m max,由力的平衡条件有
F=m maxg火 ⑦
联立⑤⑥⑦式并代入题给数据得
m max=1 875 kg⑧
在悬停避障阶段,能借助该变推力发动机实现悬停的探测器的最大质量约为1 875 kg。
高考模拟练
1.A 设火星的近地卫星的周期为T0,天问一号的半长轴为r=≈10R,由开普勒第三定律有=,解得T0=;对火星的近地卫星有G=mR,解得火星的质量为M=,火星的体积V=πR3,则火星的密度约为ρ==,选项A正确。
2.D 卫星做匀速圆周运动,根据万有引力提供向心力,有G=m,可得v=,而三个轨道半径满足rA=rB>rC,故在轨道A、B、C上运动的卫星的线速度大小关系为vA=vBrC,可推得TA>TC,选项C错误;在轨道A、B、C上运动的卫星均绕地球做圆周运动,根据开普勒第三定律可知这些卫星周期的平方和轨道半径三次方的比值相等,选项D正确。
3.A N要与M对接,需加速变轨到较高的轨道运行,故A正确;让M降低到N所在轨道上,需开启卫星M上的小发动机,使卫星M减速,而卫星M的能源耗尽了,无法开启小发动机,故B错误;由=m可得v=,可知M的线速度小于N的线速度,故C错误;由G=mω2r可得ω=,可知N的角速度比M的大,所以M、N和地球球心三者可能处在同一直线上,故D错误。
4.BC 卫星绕行星做圆周运动,根据万有引力提供向心力,得G=mr,解得T2=r3,两边取对数整理得lg T=lg r+lg =lg r-lg 。由图可知,卫星M在点1对应的周期小于在点2对应的周期,根据ω=可知,卫星M在点1对应的角速度大于在点2对应的角速度,选项A错误;根据图像及函数关系式分析,因为图像a的纵截距绝对值较小,所以行星P的质量小于行星Q的质量,根据万有引力提供向心力得G=m,解得v=,由于卫星M的中心天体质量较小,轨道半径较大,所以卫星M在点2对应的线速度小于卫星N在点3对应的线速度,选项B正确,D错误;根据函数关系式可知,两图线的斜率相等,与中心天体即行星质量无关,选项C正确。
5.D A、B构成双星系统,黑洞A的运行角速度等于黑洞B的运行角速度,选项B错误;根据牛顿第二定律有G=M1ω2·OA、G=M2ω2·OB,根据题意OA>OB,解得M16.答案 见解析
解析 (1)设质量为m的物体在地球表面附近绕地球做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律,有=,解得v1=。
(2)错误原因:随着竖直上抛物体高度的升高,离地面越来越远,万有引力越来越小,重力加速度的值会越来越小。
由于物体上升过程中做减速运动的加速度越来越小,因此物体上升的最大高度应该大于做匀减速运动上升的高度,即物体上升的最大高度应该大于。
(3)物体上升过程中速度与加速度方向相反,所以速度不断减小;上升过程中物体所受的万有引力越来越小,加速度也越来越小。物体下降过程中,速度与加速度方向相同,所以速度不断增大;下降过程中物体所受的万有引力越来越大,加速度也越来越大。v-t图像如图所示:
综合拔高练
五年高考练
考点1 万有引力定律及其应用
1.(2022广东,2)“祝融号”火星车需要“休眠”以度过火星寒冷的冬季。假设火星和地球的冬季是各自公转周期的四分之一,且火星的冬季时长约为地球的1.88倍。火星和地球绕太阳的公转均可视为匀速圆周运动。下列关于火星、地球公转的说法正确的是 ( )
A.火星公转的线速度比地球的大
B.火星公转的角速度比地球的大
C.火星公转的半径比地球的小
D.火星公转的加速度比地球的小
2.(2022全国乙,14)2022年3月,中国航天员翟志刚、王亚平、叶光富在离地球表面约400 km的“天宫二号”空间站上通过天地连线,为同学们上了一堂精彩的科学课。通过直播画面可以看到,在近地圆轨道上飞行的“天宫二号”中,航天员可以自由地漂浮,这表明他们( )
A.所受地球引力的大小近似为零
B.所受地球引力与飞船对其作用力两者的合力近似为零
C.所受地球引力的大小与其随飞船运动所需向心力的大小近似相等
D.在地球表面上所受引力的大小小于其随飞船运动所需向心力的大小
3.(2021广东,2)2021年4月,我国自主研发的空间站“天和”核心舱成功发射并入轨运行。若核心舱绕地球的运行可视为匀速圆周运动,已知引力常量,由下列物理量能计算出地球质量的是 ( )
A.核心舱的质量和绕地半径
B.核心舱的质量和绕地周期
C.核心舱的绕地角速度和绕地周期
D.核心舱的绕地线速度和绕地半径
4.(2021全国乙,18)科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示。科学家认为S2的运动轨迹是半长轴约为1 000 AU(太阳到地球的距离为1 AU)的椭圆,银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M,可以推测出该黑洞质量约为 ( )
A.4×104M B.4×106M
C.4×108M D.4×1010M
考点2 宇宙速度 人造卫星
5.(2022山东,6)“羲和号”是我国首颗太阳探测科学技术试验卫星。如图所示,该卫星围绕地球的运动视为匀速圆周运动,轨道平面与赤道平面接近垂直。卫星每天在相同时刻、沿相同方向经过地球表面A点正上方,恰好绕地球运行n圈。已知地球半径为R,自转周期为T,地球表面重力加速度为g,则“羲和号”卫星轨道距地面高度为 ( )
A.-R B.
C.-R D.
6.(2021河北,4)“祝融号”火星车登陆火星之前,“天问一号”探测器沿椭圆形的停泊轨道绕火星飞行,其周期为2个火星日。假设某飞船沿圆轨道绕火星飞行,其周期也为2个火星日。已知一个火星日的时长约为一个地球日,火星质量约为地球质量的0.1倍,则该飞船的轨道半径与地球同步卫星的轨道半径的比值约为 ( )
A. B.
C. D.
7.(2021全国甲,18)2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入运行周期约为1.8×105 s的椭圆形停泊轨道,轨道与火星表面的最近距离约为2.8×105 m。已知火星半径约为3.4×106 m,火星表面处自由落体的加速度大小约为3.7 m/s2,则“天问一号”的停泊轨道与火星表面的最远距离约为 ( )
A.6×105 m B.6×106 m
C.6×107 m D.6×108 m
8.(2021湖南,7)(多选)2021年4月29日,中国空间站天和核心舱发射升空,准确进入预定轨道。根据任务安排,后续将发射问天实验舱和梦天实验舱,计划2022年完成空间站在轨建造。核心舱绕地球飞行的轨道可视为圆轨道,轨道离地面的高度约为地球半径的 。下列说法正确的是 ( )
A.核心舱进入轨道后所受地球的万有引力大小约为它在地面时的倍
B.核心舱在轨道上飞行的速度大于7.9 km/s
C.核心舱在轨道上飞行的周期小于24 h
D.后续加挂实验舱后,空间站由于质量增大,轨道半径将变小
9.(2020课标Ⅲ,16)“嫦娥四号”探测器于2019年1月在月球背面成功着陆,着陆前曾绕月球飞行,某段时间可认为绕月做匀速圆周运动,圆周半径为月球半径的K倍。已知地球半径R是月球半径的P倍,地球质量是月球质量的Q倍,地球表面重力加速度大小为g。则“嫦娥四号”绕月球做圆周运动的速率为 ( )
A. B.
C. D.
10.(2020江苏单科,7)(多选)甲、乙两颗人造卫星质量相等,均绕地球做圆周运动,甲的轨道半径是乙的2倍。下列应用公式进行的推论正确的有 ( )
A.由v=可知,甲的速度是乙的倍
B.由a=ω2r可知,甲的向心加速度是乙的2倍
C.由F=G可知,甲的向心力是乙的
D.由=k可知,甲的周期是乙的2倍
11.(2022湖南,8)(多选)如图,火星与地球近似在同一平面内,绕太阳沿同一方向做匀速圆周运动,火星的轨道半径大约是地球的1.5倍。地球上的观测者在大多数的时间内观测到火星相对于恒星背景由西向东运动,称为顺行;有时观测到火星由东向西运动,称为逆行。当火星、地球、太阳三者在同一直线上,且太阳和火星位于地球两侧时,称为火星冲日。忽略地球自转,只考虑太阳对行星的引力,下列说法正确的是 ( )
A.火星的公转周期大约是地球的倍
B.在冲日处,地球上的观测者观测到火星的运动为顺行
C.在冲日处,地球上的观测者观测到火星的运动为逆行
D.在冲日处,火星相对于地球的速度最小
12.(2021重庆,8)(多选)2021年5月15日“祝融号”火星车成功着陆火星表面,是我国航天事业发展中具有里程碑意义的进展。此前我国“玉兔二号”月球车首次实现月球背面软着陆,若“祝融号”的质量是“玉兔二号”的K倍,火星的质量是月球的N倍,火星的半径是月球的P倍,火星与月球均视为球体,则 ( )
A.火星的平均密度是月球的倍
B.火星的第一宇宙速度是月球的倍
C.火星的重力加速度大小是月球表面的倍
D.火星对“祝融号”引力的大小是月球对“玉兔二号”引力的倍
13.(2021辽宁,8)2021年2月,我国首个火星探测器“天问一号”实现了对火星的环绕。若已知该探测器在近火星圆轨道与在近地球圆轨道运行的速率比和周期比,则可求出火星与地球的 ( )
A.半径比 B.质量比
C.自转角速度比 D.公转轨道半径比
14.(2021福建,13)一火星探测器着陆火星之前,需经历动力减速、悬停避障两个阶段。在动力减速阶段,探测器速度大小由96 m/s减小到0,历时80 s。在悬停避障阶段,探测器启用最大推力为7 500 N的变推力发动机,在距火星表面约百米高度处悬停,寻找着陆点。已知火星半径约为地球半径的,火星质量约为地球质量的,地球表面重力加速度大小取10 m/s2,探测器在动力减速阶段的运动视为竖直向下的匀减速运动。求:
(1)在动力减速阶段,探测器的加速度大小和下降距离;
(2)在悬停避障阶段,能借助该变推力发动机实现悬停的探测器的最大质量。
高考模拟练
应用实践
1.如图为“天问一号”探测器进入火星停泊轨道(椭圆轨道)。若火星可视为半径为R质量均匀分布的球体,轨道的近火点P到火星表面的距离为L1,远火点Q到火星表面的距离为L2,已知探测器在轨道上运行的周期为T,L1+L2≈18R,引力常量为G。则火星的密度约为 ( )
A. B.
C. D.
2.如图是北斗卫星导航系统中三个卫星的圆轨道示意图,其中A为地球赤道同步轨道;轨道B为倾斜同步轨道,轨道半径与地球赤道同步轨道半径相同;轨道C为中圆地球轨道。则下列说法中正确的是 ( )
A.在轨道A、B、C上运动的卫星的线速度大小关系为vA=vB>vC
B.在轨道A、B上运动的卫星需要的向心力大小一定相等
C.在轨道A、C上运动的卫星周期关系为TA
3.在人类太空征服史中,让人类遗憾的是“太空加油站”的缺乏。当通信卫星轨道校正能源耗尽的时候,它的生命就走到了尽头,有很多成了太空垃圾。如今“轨道康复者”是救助此类卫星的新型太空航天器,图甲是“轨道康复者”航天器在给太空中“垃圾”卫星补充能源,可简化为图乙所示的模型。下列说法正确的是 ( )
A.“轨道康复者”N从图乙所示轨道上加速,与卫星M对接补充能源后开启M上的小发动机向前喷气,能校正卫星M到较低的轨道运行
B.让M降低到N所在轨道上,补充能源后再开启卫星M上的小发动机向前喷气末进行校正
C.在图乙中M的线速度一定大于N的线速度
D.在图乙中,M、N和地球球心三者不可能处在同一直线上
4.(多选)如图所示是卫星绕行星沿不同轨道运动的lg T-lg r图像,其中T为卫星的周期,r为卫星的轨道半径。卫星M绕行星P运动的图线是a,卫星N绕行星Q运动的图线是b,若卫星绕行星的运动可以看成匀速圆周运动,则 ( )
A.卫星M在点1对应的角速度小于在点2对应的角速度
B.卫星M在点2对应的线速度小于卫星N在点3对应的线速度
C.直线的斜率与行星质量无关
D.行星P的质量大于行星Q的质量
5.如图甲所示,河外星系中两黑洞A、B的质量分别为M1和M2,它们以两者连线上的某一点为圆心做匀速圆周运动。为研究方便简化为如图乙所示示意图,黑洞A和黑洞B均可看成球体,OA>OB,且黑洞A的半径大于黑洞B的半径。根据你所学知识,下列说法正确的是 ( )
A.两黑洞质量之间的关系一定是M1>M2
B.黑洞A的运行角速度小于黑洞B的运行角速度
C.若两黑洞间的距离一定,把黑洞A上的物质移到黑洞B上,则它们间的万有引力会变大
D.人类要把宇航器发射到距黑洞A较近的区域进行探索,发射速度一定大于第三宇宙速度
迁移创新
6.已知地球质量为M,引力常量为G。将地球视为半径为R、质量均匀分布的球体。在以下问题的讨论中,空气阻力及地球自转的影响均忽略不计。
(1)物体在地面附近绕地球做匀速圆周运动的速度,叫作第一宇宙速度。请证明第一宇宙速度的大小v1=。
(2)某同学设想从地面以第一宇宙速度v1竖直上抛一可视为质点的物体,关于物体上升的最大高度,他的解答过程如下:
设物体的质量为m,上升的最大高度为h,重力加速度为g,由机械能守恒定律有m=mgh
又v1=,=mg,所以v1=
联立得h=。老师说该同学的上述解答是不正确的,请指出上述解答错误的原因,并分析说明物体上升的最大高度h应该比大还是小
(3)试分析说明第(2) 问中将物体以第一宇宙速度v1竖直上抛至物体落回抛出点的整个过程中,物体的速度和加速度的变化情况,并以竖直向上为正方向,在图中定性画出物体从抛出到落回抛出点的整个过程中速度随时间变化的v-t图像。
答案与分层梯度式解析
第三章 万有引力定律
综合拔高练
五年高考练
1.D 由题意可知T火=1.88T地,结合开普勒第三定律有=,整理可得=,可见r火>r地,故C错误;由=m,得v=,可见v火
3.D 核心舱绕地球做匀速圆周运动,有==mω2r=mr,核心舱的质量在求地球质量时会被约掉,已知核心舱绕地线速度和半径或者绕地角速度和半径或者绕地周期和半径即可求出地球质量,则D正确。故选D项。
4.B 地球绕太阳做匀速圆周运动,太阳对地球的万有引力提供地球做圆周运动所需向心力,有=mr,化简得=M,由此推断S2绕黑洞做椭圆运动时,半长轴的三次方与周期二次方的比值与黑洞质量成正比,有=,由观测推算S2的周期约为16年,代入数据解得M黑≈4×106M,选B。
5.C 根据题意,卫星绕地球的周期t=,设地球质量为M,地心与卫星中心距离为r,卫星绕地球做匀速圆周运动,根据万有引力提供向心力可知=mr,则GM=r3,且GM=gR2,h=r-R,代入化简得h=-R,故选C。
6.D 由万有引力提供向心力得=m
解得r=
即飞船轨道半径r飞=
地球同步卫星轨道半径r同=
由题可知T飞=2T同,M火=0.1 M地
可得=,故选D。
7.C 设火星的质量为M,半径为R,自由落体的加速度为g火,则有=mg火,设其近地卫星做圆周运动的周期为T,则有=mR,设探测器所在椭圆形停泊轨道的半长轴为a,根据开普勒第三定律得=,联立上述方程并代入数据解得a≈×107 m,可得停泊轨道与火星表面的最远距离约为2a-2.8×105 m-2×3.4×106 m≈6×107 m,故选项C正确,选项A、B、D错误。故选C项。
8.AC 核心舱在地面上所受万有引力F0=G ,入轨后,所受万有引力F=G =F0,选项A正确;核心舱绕地球运行的最大速度为7.9 km/s,选项B错误;核心舱轨道半径小于地球同步卫星的轨道半径,其周期小于24 h,选项C正确;根据G =,可知r= ,空间站的轨道半径与其速度v有关,与其质量无关,选项D错误。
9.D 设月球质量为m、半径为r
则地球质量为Qm、半径R=Pr
探测器绕月运动半径为Kr=K· ①
地球表面重力加速度大小为g,则=m0g ②
探测器绕月运动,由牛顿第二定律得
=m' ③
由①②③式得v=,故D正确。
10.CD 由=mg可知,在离地不同高度处重力加速度不同,而A项推论误将g作为一个常量,故A项所得结果错误。同理由=mrω2可知卫星在不同轨道上运行的角速度不同,B项将ω作为常量做出的推论也是错误的。由万有引力定律可知C项正确。由=mr可得=,可见k=是一个只与地球质量有关的物理量,故D项由此所得推论是正确的。
11.CD 由开普勒第三定律有=,得==,A错误;由=m,得v=,故v火
13.AB 探测器绕火星和地球的运动均可视为匀速圆周运动。
根据v=
得r=
故=
故火星与地球的半径比可求,A正确;
以探测器为研究对象,环绕过程中万有引力提供向心力,有
G=
中心天体的质量M=
故=
故火星和地球的质量比可求,B正确;
火星与地球的公转轨道半径比和自转角速度比由于条件不足,无法求得,故C、D错误。
14.答案 (1)1.2 m/s2 3 840 m (2)1 875 kg
解析 (1)设探测器在动力减速阶段所用时间为t,初速度大小为v1,末速度大小为v2,加速度大小为a,由匀变速直线运动速度公式有
v2=v1-at ①
代入题给数据得
a=1.2 m/s2 ②
设探测器下降的距离为s,由匀变速直线运动位移公式有
s=v1t-at2 ③
联立②③式并代入题给数据得
s=3 840 m④
(2)设火星的质量、半径和表面重力加速度大小分别为M火、r火、g火,地球的质量、半径和表面重力加速度大小分别为M地、r地、g地。由牛顿运动定律和万有引力定律,对星球表面质量为m的物体有
=mg火 ⑤
=mg地 ⑥
式中G为引力常量。设变推力发动机的最大推力为F,能够悬停的火星探测器最大质量为m max,由力的平衡条件有
F=m maxg火 ⑦
联立⑤⑥⑦式并代入题给数据得
m max=1 875 kg⑧
在悬停避障阶段,能借助该变推力发动机实现悬停的探测器的最大质量约为1 875 kg。
高考模拟练
1.A 设火星的近地卫星的周期为T0,天问一号的半长轴为r=≈10R,由开普勒第三定律有=,解得T0=;对火星的近地卫星有G=mR,解得火星的质量为M=,火星的体积V=πR3,则火星的密度约为ρ==,选项A正确。
2.D 卫星做匀速圆周运动,根据万有引力提供向心力,有G=m,可得v=,而三个轨道半径满足rA=rB>rC,故在轨道A、B、C上运动的卫星的线速度大小关系为vA=vB
3.A N要与M对接,需加速变轨到较高的轨道运行,故A正确;让M降低到N所在轨道上,需开启卫星M上的小发动机,使卫星M减速,而卫星M的能源耗尽了,无法开启小发动机,故B错误;由=m可得v=,可知M的线速度小于N的线速度,故C错误;由G=mω2r可得ω=,可知N的角速度比M的大,所以M、N和地球球心三者可能处在同一直线上,故D错误。
4.BC 卫星绕行星做圆周运动,根据万有引力提供向心力,得G=mr,解得T2=r3,两边取对数整理得lg T=lg r+lg =lg r-lg 。由图可知,卫星M在点1对应的周期小于在点2对应的周期,根据ω=可知,卫星M在点1对应的角速度大于在点2对应的角速度,选项A错误;根据图像及函数关系式分析,因为图像a的纵截距绝对值较小,所以行星P的质量小于行星Q的质量,根据万有引力提供向心力得G=m,解得v=,由于卫星M的中心天体质量较小,轨道半径较大,所以卫星M在点2对应的线速度小于卫星N在点3对应的线速度,选项B正确,D错误;根据函数关系式可知,两图线的斜率相等,与中心天体即行星质量无关,选项C正确。
5.D A、B构成双星系统,黑洞A的运行角速度等于黑洞B的运行角速度,选项B错误;根据牛顿第二定律有G=M1ω2·OA、G=M2ω2·OB,根据题意OA>OB,解得M1
解析 (1)设质量为m的物体在地球表面附近绕地球做匀速圆周运动,万有引力提供向心力,根据牛顿第二定律,有=,解得v1=。
(2)错误原因:随着竖直上抛物体高度的升高,离地面越来越远,万有引力越来越小,重力加速度的值会越来越小。
由于物体上升过程中做减速运动的加速度越来越小,因此物体上升的最大高度应该大于做匀减速运动上升的高度,即物体上升的最大高度应该大于。
(3)物体上升过程中速度与加速度方向相反,所以速度不断减小;上升过程中物体所受的万有引力越来越小,加速度也越来越小。物体下降过程中,速度与加速度方向相同,所以速度不断增大;下降过程中物体所受的万有引力越来越大,加速度也越来越大。v-t图像如图所示:
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
