四川省广安市广安区等3地2024-2025学年高一下学期7月期末统测数学试卷(含答案)
文档属性
| 名称 | 四川省广安市广安区等3地2024-2025学年高一下学期7月期末统测数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 576.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 00:00:00 | ||
图片预览




文档简介
数学试卷
注意事项
本试卷满分150分,考试时间120分钟。
答题前, 务必将自己的姓名、准考证号填写在答题卡规定的位置上。
答选择题时,必须使用2B铅笔填涂对应题目的答案标号,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
考试结束后, 将答题卡、试卷、草稿纸全部交回。
请考生注意:所有题目必须在答题卡上作答,在试题卷上答题无效。
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知为复数的共轭复数,则( )
A. B. C. D.2
2.把函数的图象向右平移个单位长度后得到函数的图象,若的图象关于点对称,则的最小值为( )
A. B. C. D.
3.2024年4月21日,13000多人参赛的2024阜阳马拉松在市规划展示馆旁鸣枪起跑.经过激烈角逐,前八名的成绩(单位:小时)分别为,则这组数据的分位数是( )
A. B. C. D.
4.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面积和球的表面积之比为( )
A. B. C. D.
5.如图,是边长为4的正方形,若,且为的中点,则( )
A.3 B.4 C.5 D.6
6.关于函数,有下列命题:
①直线是图象的一条对称轴
②存在,使得恒成立;
③在区间上单调递增
④的图象可以由函数向右平移个单位得到
则其中真命题的个数为( )
A.0 B.1 C.2 D.3
7.一副三角板由一块有一个内角为的直角三角形和一块等腰直角三角形组成,如图所示,,,,.现将两块三角板拼接在一起,取中点与中点,则下列直线与平面所成的角不为定值的是( )
A. B. C. D.
8.已知函数为偶函数,当时,,那么函数的零点个数为( )
A.2 B.4 C.6 D.8
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知复数,其中i是虚数单位,则以下说法正确的是( )
A.复数z的实部为3 B.复数z的虚部为2i
C.复数z的模为 D.复数z的共轭复数
10.下列四个命题中正确的是
A.如果一条直线不在某个平面内,那么这条直线就与这个平面平行
B.过直线外一点有无数个平面与这条直线平行
C.过平面外一点有无数条直线与这个平面平行
D.过空间一点必存在某个平面与两条异面直线都平行
11.已知锐角三个内角的对应边分别为,且.则下列结论正确的是( )
A.的面积最大值为
B.的取值范围为
C.的值可能为3
D.的最小值为
三、填空题:本题共3小题,每小题 5 分,共15分。
12.由于甲流暴发,防疫站对学生进行身体健康调查,对男女学生采用分层抽样法抽取. 学校共有学生1600名,抽取一个容量为200的样本.已知女生比男生少抽了20人,则该校的女生人数应是 人.
13.若,且,则向量与的夹角为 .
14.在四面体中,,则该四面体的外接球的表面积为 .
四、解答题:本大题共5小题,共77分。解答应写出必要的文字说明、证明过程或演算步骤。
15.2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:.把年龄落在区间和 内的人分别称为 “青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
(2)根据已知条件完成下面的列联表,并判断能否有的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
附:参考公式,其中.
临界值表:
16.已知向量为平面向量,且,
(1)若的夹角为,求及
(2)若是与平行的向量,求的坐标.
17.已知向量,,设函数.
(1)求函数的单调递增区间及其图象的对称轴方程;
(2)已知分别为三角形的内角对应的三边长,为锐角,,且恰是函数在上的最大值,求三角形的面积.
18.已知,设函数的表达式为(其中)
(1)设,,求曲线在点处的切线方程;
(2)设,,集合,记,若在D上有两个不同的极值点,求b的取值范围;
(3)当,,时,记,其中n为正整数.求证:.
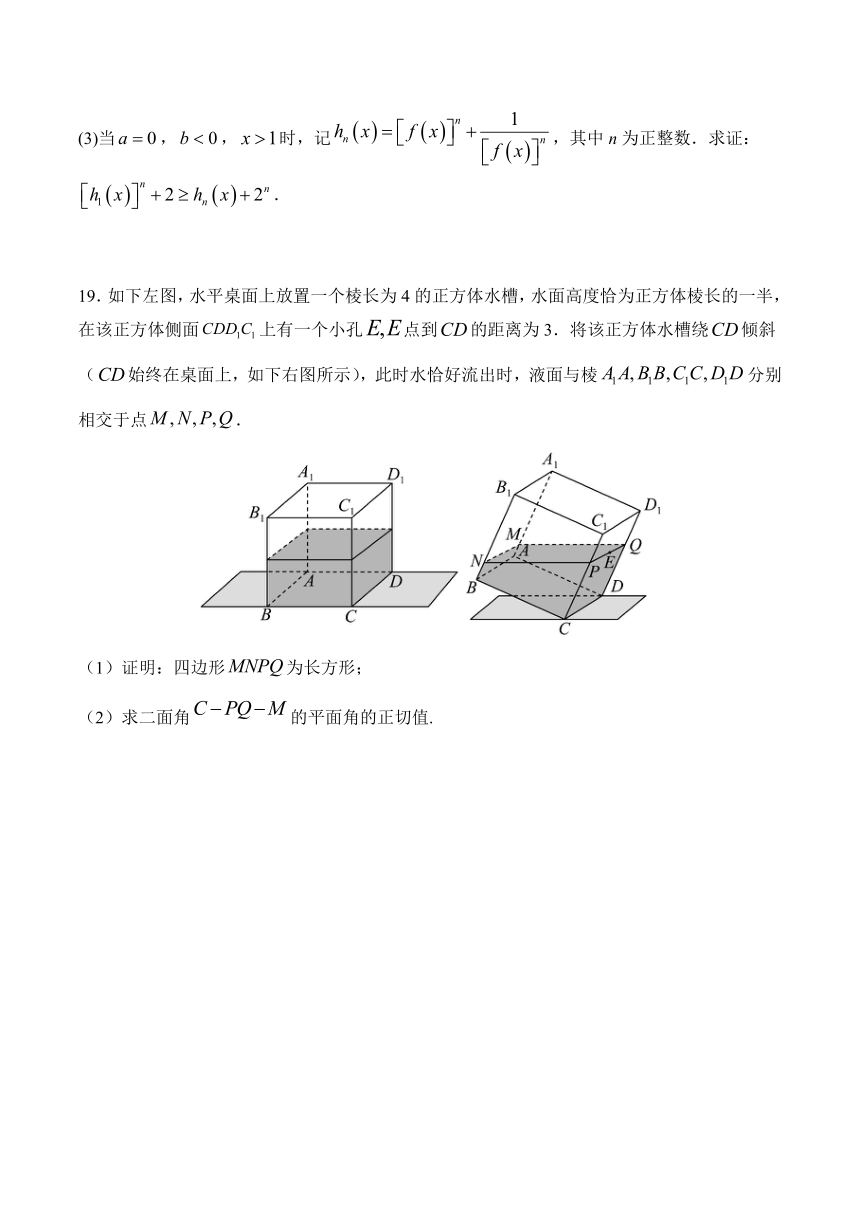
19.如下左图,水平桌面上放置一个棱长为4的正方体水槽,水面高度恰为正方体棱长的一半,在该正方体侧面上有一个小孔点到的距离为3.将该正方体水槽绕倾斜(始终在桌面上,如下右图所示),此时水恰好流出时,液面与棱分别相交于点.
(1)证明:四边形为长方形;
(2)求二面角的平面角的正切值.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
D C C C C B B D AC BC BC 720
15.(1)根据频率分布直方图可知样本的众数为40,因为,
设样本的中位数为,则,所以,即样本的中位数约为36.43.
(2)依题意可知,抽取的“青少年”共有人,“中老年”共有人.
完成的列联表如下:
关注 不关注 合计
青少年 15 30 45
中老年 35 20 55
合计 50 50 100
结合列联表的数据得 ,
因为,
所以有的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”.
16.(1)易知,
,
所以,
,
所以.
(2)由题意得:,且,
解得:或,
所以或
17.(1)
,
由,,得,
所以函数的单调递增区间为,,
令,,解得,
所以曲线的对称轴方程为,.
(2)由(1)知,
当时,则当即时函数取得最大值,
又恰是函数在上的最大值,且为锐角,可得,
由余弦定理可得,解得或,
当时,三角形的面积,
当时,三角形的面积.
所以三角形的面积为或.
18.(1)由,,可知,则,
当时,,
所以在点处的切线方程为:,即为;
(2)当时,由,则,
即,
由在上有两个不同的极值点,则在内有两个解,
即由等价于, 作出二次函数图象,
因为当时,,
结合图像可知:当时,方程在内有两个解,
即b的取值范围;
(3)证明:依题意,,,且,,
令,则
所以
而
,
则
又,且,当且仅当时等号成立,所以,
同理,,……,且均在时等号成立,
所以
,即得证.
19.(1)因为平面平面,平面平面,
平面,所以,
因为平面平面,平面平面,
平面,所以,
所以四边形是平行四边形,
因为始终在桌面上,所以,在长方体中,
平面,平面,所以,
即,所以四边形是长方形.
(2)由题意知,水的体积为,如图所示,
正方体水槽绕倾斜水面分别与棱交于,
则,水的体积为,
所以,即,所以,
在平面内,过点作,交于,
则四边形是平行四边形,,
所以,
因为,,所以,由(1),
所以即为二面角的平面角,
又,,所以,
在中,,
所以侧面与桌面所成的角的正切值为2.
注意事项
本试卷满分150分,考试时间120分钟。
答题前, 务必将自己的姓名、准考证号填写在答题卡规定的位置上。
答选择题时,必须使用2B铅笔填涂对应题目的答案标号,如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
考试结束后, 将答题卡、试卷、草稿纸全部交回。
请考生注意:所有题目必须在答题卡上作答,在试题卷上答题无效。
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知为复数的共轭复数,则( )
A. B. C. D.2
2.把函数的图象向右平移个单位长度后得到函数的图象,若的图象关于点对称,则的最小值为( )
A. B. C. D.
3.2024年4月21日,13000多人参赛的2024阜阳马拉松在市规划展示馆旁鸣枪起跑.经过激烈角逐,前八名的成绩(单位:小时)分别为,则这组数据的分位数是( )
A. B. C. D.
4.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面积和球的表面积之比为( )
A. B. C. D.
5.如图,是边长为4的正方形,若,且为的中点,则( )
A.3 B.4 C.5 D.6
6.关于函数,有下列命题:
①直线是图象的一条对称轴
②存在,使得恒成立;
③在区间上单调递增
④的图象可以由函数向右平移个单位得到
则其中真命题的个数为( )
A.0 B.1 C.2 D.3
7.一副三角板由一块有一个内角为的直角三角形和一块等腰直角三角形组成,如图所示,,,,.现将两块三角板拼接在一起,取中点与中点,则下列直线与平面所成的角不为定值的是( )
A. B. C. D.
8.已知函数为偶函数,当时,,那么函数的零点个数为( )
A.2 B.4 C.6 D.8
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.已知复数,其中i是虚数单位,则以下说法正确的是( )
A.复数z的实部为3 B.复数z的虚部为2i
C.复数z的模为 D.复数z的共轭复数
10.下列四个命题中正确的是
A.如果一条直线不在某个平面内,那么这条直线就与这个平面平行
B.过直线外一点有无数个平面与这条直线平行
C.过平面外一点有无数条直线与这个平面平行
D.过空间一点必存在某个平面与两条异面直线都平行
11.已知锐角三个内角的对应边分别为,且.则下列结论正确的是( )
A.的面积最大值为
B.的取值范围为
C.的值可能为3
D.的最小值为
三、填空题:本题共3小题,每小题 5 分,共15分。
12.由于甲流暴发,防疫站对学生进行身体健康调查,对男女学生采用分层抽样法抽取. 学校共有学生1600名,抽取一个容量为200的样本.已知女生比男生少抽了20人,则该校的女生人数应是 人.
13.若,且,则向量与的夹角为 .
14.在四面体中,,则该四面体的外接球的表面积为 .
四、解答题:本大题共5小题,共77分。解答应写出必要的文字说明、证明过程或演算步骤。
15.2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:.把年龄落在区间和 内的人分别称为 “青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
(2)根据已知条件完成下面的列联表,并判断能否有的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
附:参考公式,其中.
临界值表:
16.已知向量为平面向量,且,
(1)若的夹角为,求及
(2)若是与平行的向量,求的坐标.
17.已知向量,,设函数.
(1)求函数的单调递增区间及其图象的对称轴方程;
(2)已知分别为三角形的内角对应的三边长,为锐角,,且恰是函数在上的最大值,求三角形的面积.
18.已知,设函数的表达式为(其中)
(1)设,,求曲线在点处的切线方程;
(2)设,,集合,记,若在D上有两个不同的极值点,求b的取值范围;
(3)当,,时,记,其中n为正整数.求证:.
19.如下左图,水平桌面上放置一个棱长为4的正方体水槽,水面高度恰为正方体棱长的一半,在该正方体侧面上有一个小孔点到的距离为3.将该正方体水槽绕倾斜(始终在桌面上,如下右图所示),此时水恰好流出时,液面与棱分别相交于点.
(1)证明:四边形为长方形;
(2)求二面角的平面角的正切值.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
D C C C C B B D AC BC BC 720
15.(1)根据频率分布直方图可知样本的众数为40,因为,
设样本的中位数为,则,所以,即样本的中位数约为36.43.
(2)依题意可知,抽取的“青少年”共有人,“中老年”共有人.
完成的列联表如下:
关注 不关注 合计
青少年 15 30 45
中老年 35 20 55
合计 50 50 100
结合列联表的数据得 ,
因为,
所以有的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”.
16.(1)易知,
,
所以,
,
所以.
(2)由题意得:,且,
解得:或,
所以或
17.(1)
,
由,,得,
所以函数的单调递增区间为,,
令,,解得,
所以曲线的对称轴方程为,.
(2)由(1)知,
当时,则当即时函数取得最大值,
又恰是函数在上的最大值,且为锐角,可得,
由余弦定理可得,解得或,
当时,三角形的面积,
当时,三角形的面积.
所以三角形的面积为或.
18.(1)由,,可知,则,
当时,,
所以在点处的切线方程为:,即为;
(2)当时,由,则,
即,
由在上有两个不同的极值点,则在内有两个解,
即由等价于, 作出二次函数图象,
因为当时,,
结合图像可知:当时,方程在内有两个解,
即b的取值范围;
(3)证明:依题意,,,且,,
令,则
所以
而
,
则
又,且,当且仅当时等号成立,所以,
同理,,……,且均在时等号成立,
所以
,即得证.
19.(1)因为平面平面,平面平面,
平面,所以,
因为平面平面,平面平面,
平面,所以,
所以四边形是平行四边形,
因为始终在桌面上,所以,在长方体中,
平面,平面,所以,
即,所以四边形是长方形.
(2)由题意知,水的体积为,如图所示,
正方体水槽绕倾斜水面分别与棱交于,
则,水的体积为,
所以,即,所以,
在平面内,过点作,交于,
则四边形是平行四边形,,
所以,
因为,,所以,由(1),
所以即为二面角的平面角,
又,,所以,
在中,,
所以侧面与桌面所成的角的正切值为2.
同课章节目录
