四年级暑假新课提升预习练第三单元《角的度量》(含解析)-2024-2025学年下学期小学数学人教版
文档属性
| 名称 | 四年级暑假新课提升预习练第三单元《角的度量》(含解析)-2024-2025学年下学期小学数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 290.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-24 19:27:56 | ||
图片预览




文档简介
四年级暑假新课提升预习练第三单元《角的度量》(含解析)-2024-2025学年下学期小学数学人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面可以两端无限延长的是( )。
A.线段 B.射线 C.直线 D.以上答案都对
2.下面的每组时刻中,钟面上的时针与分针组成的角大小不同的是( )。
A.3:00和9:00 B.4:00和7:00 C.1:00和11:00
3.时针走3小时转过的角度是( )。
A.30° B.60° C.90° D.180°
4.体育课上,体育老师让我们向后转时,右脚所转的角应该是一个( )角。
A.锐角 B.直角 C.平角 D.周角
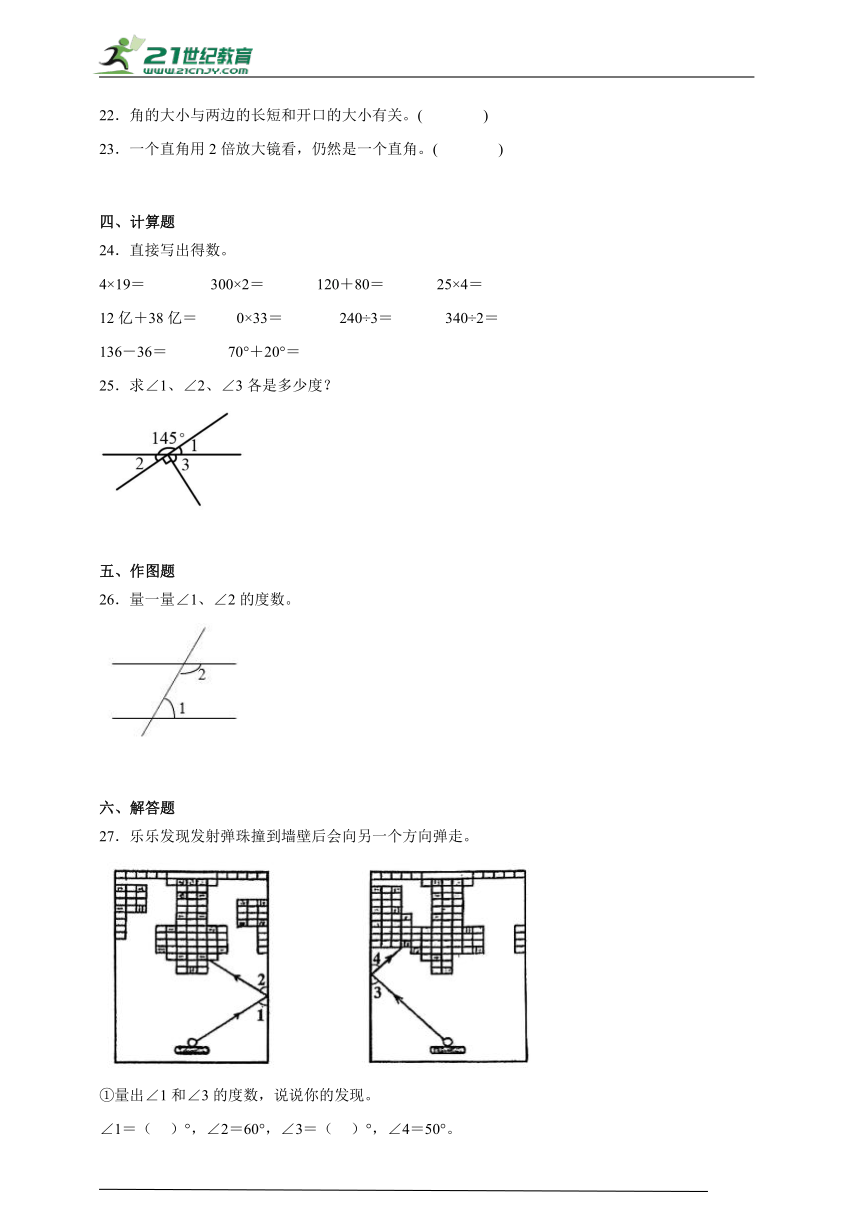
5.下面各角,度数最大的是( )。
A. B. C. D.
6.用一副三角尺不能画出的角是( )。
A.150° B.75° C.40° D.15°
7.钟面上时针、分针成90°角时,这时的时间可能是选项中的( )。
A.2时 B.6时 C.9时 D.4时
8.用一副三角尺不能拼成的角是( )。
A.75° B.105° C.130°
9.把一个平角分成两个角,其中一个角是锐角,另一个角( )。
A.可能是锐角,也可能是钝角 B.可能是直角
C.一定是钝角 D.不确定
二、填空题
10.如图所示,钟面上时针和分针构成的较小角是( )角;分针走一圈,旋转了( )度。
11.如下图,一面镜子反射一条光线。已知∠2=∠3,∠4=140°,那么∠1= 。
12.如图,把两个三角尺叠在一起,已知∠2=40°,那么∠1+∠2+∠3=( )°。
13.下午3时整,钟面上的时针与分针所成的是( )角,下午( )时整,钟面上的时针与分针所成的是平角。
14.下图的射线可以命名为( ),如果这条射线绕点A旋转半周是( )度,旋转一周是( )度。
15.钟面上分针从6走到12形成的角是( )°,分针从9走到12形成的角是( )°,分针从2走到4形成的角是( )°。
16.钟面上( )时整,时针和分针成平角;( )时整或( )时整,钟面上的时针和分针所夹的较小角是30°;钟面上9时整,时针和分针所夹的较小角是( )°。
17.用量角器量出如图中角的度数。
∠1=( ) ∠2=( )
18.钟面9时整时,时针和分针所成的角是( )度,是( )角。( )时整,时针和分针所成的角是平角,是( )度。
三、判断题
19.一个15°的角在放大镜下可能变成30°的角。( )
20.平角的两条边在一条直线上,周角的两条边重合成射线。( )
21.一条长1000米的笔直的公路可以看作是直线。( )
22.角的大小与两边的长短和开口的大小有关。( )
23.一个直角用2倍放大镜看,仍然是一个直角。( )
四、计算题
24.直接写出得数。
4×19= 300×2= 120+80= 25×4=
12亿+38亿= 0×33= 240÷3= 340÷2=
136-36= 70°+20°=
25.求∠1、∠2、∠3各是多少度?
五、作图题
26.量一量∠1、∠2的度数。
六、解答题
27.乐乐发现发射弹珠撞到墙壁后会向另一个方向弹走。
①量出∠1和∠3的度数,说说你的发现。
∠1=( )°,∠2=60°,∠3=( )°,∠4=50°。
我发现:______________________
②下图中发射弹沿箭头方向发出,请你画出它弹走的方向,并判断它是否能够击中砖块A。
28.测量∠1的度数,并通过计算求出∠2的度数(要求有计算过程,写出算式)。
∠1=( )°、∠3=( )、∠2=( )。
29.下面是一张长方形纸折起来形成的图形,已知∠1=30°,∠1比∠2小多少度?
30.量出下面∠1的度数,并在下边空白处画一个60°的角。
∠1=( )°
31.画图。
(1)过一点O,能画直线吗?能画几条?
(2)经过两点A、B,能不能画直线?能画几条?
《四年级暑假新课提升预习练第三单元《角的度量》(含解析)-2024-2025学年下学期小学数学人教版》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 C B C C D C C C C
1.C
【分析】直线是直的,没有端点,无限长,可以向两端无限延长。射线是直的,有1个端点,无限长,可以向一端无限延长。线段是直的,有2个端点,有限长。
【详解】可以两端无限延长的是直线。
故答案为:C
2.B
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,钟面上3:00或9:00,时针和分针之间相差的3个大格数,用大格数3乘30°即可;钟面上4:00,时针和分针之间相差的4个大格数,用大格数4乘30°;钟面上7:00,时针和分针之间相差的5个大格数,用大格数5乘30°;钟面上1:00或11:00,时针和分针之间相差的1个大格数,用大格数1乘30°;依此计算并选择。
【详解】A.3×30°=90°,即3:00和9:00,时针与分针组成的角都是为90°。
B.4×30=120°,即4:00,时针与分针组成的角都是为120°;5×30=150°,即7:00,时针与分针组成的角都是为150°。
C.1×30°=30°,即1:00和11:00,时针与分针组成的角都是为30°。
故答案为:B
【点睛】此题考查了利用钟面上每一大格是30°的性质,来解决分针转动一定的时刻所组成夹角的度数问题的灵活应用能力。
3.C
【分析】钟面上时针走一圈是360°,钟面上有12个大格,所以每个大格是30°。时针1小时走1大格,3小时走3大格。据此可以知道走了多少度。
【详解】走一圈是360°,钟面上有12个大格,所以每个大格是30°。
30°×3=90°
所以,时针走3小时转过的角是90°。
故答案为:C
4.C
【分析】体育课上我们如果向左转或向右转时,就是由原来的方向向左或右旋转90°,即转过的角是直角;如果向后转时,就是由原来的方向向后旋转180°,即转过的角是平角。
【详解】根据分析:体育课上,体育老师让我们向后转时,右脚所转的角应该是一个平角。
故答案为:C
5.D
【分析】A.此图为直角,根据直角的特点,此图的度数等于90°。
B.此图为钝角,根据钝角的特点,此图的度数大于90°小于180°。
C.此图为平角,根据平角的特点,此图的度数等于180°。
D.此图为周角,根据周角的特点,此图的度数等于360°。
【详解】
根据分析,可知上图中度数最大的是。
故答案为:D
【点睛】本题考查的是直角、钝角、平角、周角的特点。
6.C
【分析】一副三角尺上的角有30°、45°、60°、90°,45°-30°=15°,45°+30°=75°,90°+60°=150°,45°+60°=105°,45°+90°=135°,所以用一副三角尺可以画出15°、45°、30°、75°、90°、105°、135°、150°的角,据此即可解答。
【详解】用一副三角尺可以拼出75°、15°、150°的角。
故答案为:C。
7.C
【分析】钟表上共有12个大格,每个大格是30°,90°的角需要分针与时针之间有3个大格,在3点或9点的时间恰好成90°,据此结合选项进行选择即可。
【详解】A.2时时,分针与时针之间有2个大格,时针、分针成60°角;
B.6时时,分针与时针之间有6个大格,时针、分针成180°角;
C.9时时,分针与时针之间有3个大格,时针、分针成90°角;
D.4时时,分针与时针之间有4个大格,时针、分针成120°角。
故答案为:C
【点睛】本题主要依据平时的留心观察发现,结合钟表的构造即可解答。
8.C
【分析】一副三角板中的各个角的度数分别是30°、60°、45°、90°。将它们进行组合,可得到的角有60°-45°=15°,60°+45°=105°,60°+90°=150°,90°+45°=135°,90°+30°=120°,30°+45°=75°。据此解答。
【详解】A.30°+45°=75°,用一副三角尺可以拼成75°的角;
B.60°+45°=105°,用一副三角尺可以拼成105°的角;
C.用一副三角尺不能拼成130°的角;
故答案为:C
9.C
【分析】平角是180°的角,锐角是大于0°且小于90°的角,直角是等于90°的角,钝角是大于90°且小于180°的角。据此解答。
【详解】根据分析可知:平角是180°的角,把一个平角分成两个角,其中一个角是锐角,由于锐角是小于90°的角,180°的角减去一个小于90°的角,得到的另一个角肯定是大于90°且小于180°的角,所以另一个角一定是一个钝角。
故答案为:C
10. 锐 360
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°;2时整,时针和分针之间有2个大格,所形成的较小角是2乘30°,小于90°的角为锐角;分针走一圈,旋转了1周,也就是360°;据此解答。
【详解】根据分析:2×30°=60°,60°<90°,60°为锐角,所以钟面上时针和分针构成的较小角是锐角;分针走一圈,旋转了360度。
11.100°/100度
【分析】根据题意可知∠1、∠2和∠3组成一个平角,∠1与∠2组成∠4,∠3与∠4组成一个平角,平角的度数是180°,用180°减去∠4的度数就是∠3的度数,∠2=∠3,那么再用∠4的度数减去∠2的度数即可求出∠1。
【详解】∠3:180°-∠4
=180°-140°
=40°
∠2=∠3=40°
∠1:∠4-∠2
=140°-40°
=100°
12.140
【分析】由题图可知,∠2和∠3组成三角尺的直角,即∠3=90°-∠2;∠2和∠1组成另一个三角尺的直角,即∠1=90°-∠2;又已知∠2=40°,所以可以分别求出∠3和∠1的度数,然后再把∠1、∠2和∠3这三角的度数相加,即可解答。
【详解】因为∠2=40°
∠2+∠3=90°
所以∠3=90°-∠2
=90°-40°
=50°
因为∠2=40°
∠2+∠1=90°
所以∠1=90°-∠2
=90°-40°
=50°
∠1+∠2+∠3=40°+50°+50°
=90°+50°
=140°
即如题图,把两个三角尺叠在一起,已知∠2=40°,那么∠1+∠2+∠3=140°。
13. 直 6
【分析】平角:射线OA绕着点O旋转,当终止位置OC和起始位置OA成一直线时,所成的角叫做平角。平角为180度。
直角:平角的一半叫做直角。直角为90度。
【详解】下午3时整,时针指向3,分针指向12,夹角为90度,时针与分针所成的是直角;
下午6时整,时针指向6,分针指向12,夹角为180度,时针与分针所成的是平角。
14. 射线AB 180 360
【分析】射线命名时,以端点开始,然后和射线上任意另一个点组合起来命名;
一条射线绕端点旋转半周,形成一个平角,平角的度数为180度;如果绕端点旋转一周,形成一个周角,周角的度数为360度。
【详解】这条射线可以命名为:射线AB;
这条射线绕点A旋转半周是一个平角,是180度,若旋转一周是一个周角,是360度。
15. 180 90 60
【分析】钟面一周为360°,被平均分成12个大格,每个大格对应30°。分针每走一个大格形成的角度为30°,用分针走的大格数×30°即可;钟面上分针从6走到12共走了6大格,用6×30°即可计算出钟面上分针从6走到12形成的角;分针从9走到12共走了3大格,用3×30°即可计算出钟面上分针从9走到12形成的角;分针从2走到4共走了2大格,用2×30°即可计算出钟面上分针从2走到4形成的角,据此解题。
【详解】(12-6)×30°
=6×30°
=180°
(12-9)×30°
=3×30°
=90°
(4-2)×30°
=2×30°
=60°
钟面上分针从6走到12形成的角是180°,分针从9走到12形成的角是90°,分针从2走到4形成的角是60°。
16. 6 11 1 90
【分析】钟面上有12大格,把钟面平均分成12等份,每一大格对应的夹角是30°;6时整,分针指向12,时针指向6,时针与分针在一条直线,时针和分针成平角;当11时整或1时整,时针与分针所夹的较小角正好对应一大格,是30°;钟面上9时整,时针和分针所夹的较小角正对应3大格,是30°×3=90°;据此即可解答。
【详解】根据分析可知,钟面上6时整,时针和分针成平角;11时整或1时整,钟面上的时针和分针所夹的较小角是30°;钟面上9时整,时针和分针所夹的较小角是90°。
17. 135°/135度 75°/75度
【分析】用量角器的圆点和角的顶点重合,0刻度线和角的一条边重合,另一条边在量角器上的刻度就是该角的度数,据此解答。
【详解】测量结果如下:
【点睛】本题主要考查了学生正确使用量角器测量角的能力。
18. 90 直 6 180
【分析】在9时整时,时针指向9,分针指向12,钟面上一个大格的度数为30度,所以时针与分针之间有3个大格,30×3=90(度),等于90度的角叫做直角;
等于180度的角叫做平角,整时,分针指向12,当时针指向6时,时针与分针之间有6个大格,是30×6=180(度),由此进行解答即可。
【详解】30×3=90(度)
30×6=180(度)
钟面9时整时,时针和分针所成的角是90度,是直角。6时整,时针和分针所成的角是平角,是180度。
【点睛】此题考查了钟面的认识以及角的分类,解答此题,要掌握钟面上每一大格的角度是30度。
19.×
【分析】角的大小与两边的长短无关,只与边叉开的大小有关,用放大镜看角时,放大的是角的边的长度,不改变角的形状,即边叉开的大小不变,所以用放大镜看角,角的大小不变。
【详解】根据分析可知:一个15°的角在放大镜下度数不变,原题说法错误。
故答案为:×
20.√
【分析】一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。平角的特点是两条边成一条直线;一条射线绕着它的端点旋转一周所形成的角,叫做周角。周角的特点是两条边重合成射线。据此解答。
【详解】平角的两条边在一条直线上,周角的两条边重合成射线。原题说法正确。
故答案为:√
21.×
【分析】根据直线的含义:直线没有端点,无限延长,连接两点的线段的长度叫做两点间的距离。据此判断即可。
【详解】一条长1000米的笔直的公路可以看作是线段。所以原题说法错误。
故答案为:×
22.×
【分析】从一点引出两条射线所组成的图形叫做角。角的两条边是射线,射线可以无限延伸。角的大小是指角两条边所张开的大小。根据角的组成和角的大小定义,即可解答。
【详解】根据角的含义可知,角的大小与角两边的长短无关,与角的两边叉开的大小有关,开叉越大,角就越大,反之越小,原说法错误。
故答案为:×
【点睛】正确理解角的定义,明确角的大小与角两边的长短无关,与角的两边叉开的大小有关,是解答此题的关键。
23.√
【分析】用2倍放大镜看角,只改变角两边的长度,角两边的开叉的大小不变,即角的度数不变。
【详解】一个直角用2倍放大镜看,仍然是一个直角。
故答案为:√
24.76;600;200;100;
50亿;0;80;170;
100;90°
【详解】略
25.∠1=35°;∠2=35°;∠3=55°
【分析】观察图中可知,∠1和145°角组成平角,平角=180°,因此用180°减去145°即可求出∠1的度数;∠2和145°角组成平角,因此用180°减去145°即可求出∠2的度数;∠1和∠3组成直角,直角=90°,因此用90°减去∠1的度数即可求出∠3的度数。
【详解】∠1=180°-145°=35°
∠2=180°-145°=35°
∠3=90°-35°=55°
26.∠1=60°,∠2=120°
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量即可。
【详解】根据测量可知,∠1=60°,∠2=120°。
【点睛】熟练掌握角的度量方法,是解答此题的关键。
27.(1)60;50;见详解
(2)见详解;不能
【分析】(1)根据角的度量方法:量角要注意两对齐:量角器的中心和角的顶点对齐;量角器的0刻度线和角的一条边对齐;做到两对齐后看角的另一条边对着刻度线几,这个角就是几度;看刻度要分清内外圈。比较∠1和∠2、∠3和∠4,得出发射弹沿箭头发出的射线与墙壁的角度与弹珠撞到墙壁后弹出去的射线与墙壁的角度的关系。
(2)根据发射弹沿箭头发出的射线与墙壁的角度等于弹珠撞到墙壁后弹出去的射线与墙壁的角度的关系画图即可。
【详解】①量出∠1和∠3的度数,说说你的发现。
∠1=60°,∠2=60°,∠3=50°,∠4=50°。
我发现:发射弹沿箭头发出的射线与墙壁的角度等于弹珠撞到墙壁后弹出去的射线与墙壁的角度。
②下图中发射弹沿箭头方向发出,发射弹沿箭头发出的射线与墙壁的角度等于弹珠撞到墙壁后弹出去的射线与墙壁的角度,画出图如下:
它不能击中砖块A。
28.120;60°;30°
计算过程见详解
【分析】量角器的使用方法。两合一看,两合是指中心点与角的顶点重合;0刻度线与角的一边重合。一看就是要看角的另一边所对的量角器的刻度。看角的度数时要注意是看外刻度还是内刻度。角的开口向左看外刻度线,角的开口向右看内刻度线。
根据角的度量方法,测量∠1的度数,然后根据∠1+∠3=180°,∠3=180°-∠1;∠3+∠2=90°,∠2=90°-∠3。据此解答。
【详解】测量可知∠1=120°。
∠3=180°-∠1=180°-120°=60°
∠2=90°-∠3=90°-60°=30°。
即∠1=120°、∠3=60°、∠2=30°。
29.45度
【分析】
根据题意可知,∠2=∠3,平角是180°,∠2和∠3和∠1构成一个平角,据此用180°减去∠1然后再除以2,即可求出∠2的度数,然后据此进行解题。
【详解】180-30=150(度)
150÷2=75(度)
75-30=45(度)
答:∠1比∠2小45度。
30.105;
图见详解
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量即可。
画角的步骤是:先画一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合,然后在量角器相对应的刻度线的地方点一个点,最后以画出的射线的端点为端点,通过刚画的点,再画一条射线;依此画图即可。
【详解】根据分析可量出∠1的度数,∠1=105°;画出60°的角。如图:
31.(1)能,无数条;(2)能,一条。
【分析】根据直线的性质:同一平面内,两点确定一条直线,过一点能画无数条直线;据此解答即可。
【详解】(1)根据直线的性质可知:过一点O,能画直线,且能画无数条。
(2)经过两点A、B,能画直线,且只能画一条。
【点睛】本题主要考查的是直线的性质,解题关键在于熟知概念。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面可以两端无限延长的是( )。
A.线段 B.射线 C.直线 D.以上答案都对
2.下面的每组时刻中,钟面上的时针与分针组成的角大小不同的是( )。
A.3:00和9:00 B.4:00和7:00 C.1:00和11:00
3.时针走3小时转过的角度是( )。
A.30° B.60° C.90° D.180°
4.体育课上,体育老师让我们向后转时,右脚所转的角应该是一个( )角。
A.锐角 B.直角 C.平角 D.周角
5.下面各角,度数最大的是( )。
A. B. C. D.
6.用一副三角尺不能画出的角是( )。
A.150° B.75° C.40° D.15°
7.钟面上时针、分针成90°角时,这时的时间可能是选项中的( )。
A.2时 B.6时 C.9时 D.4时
8.用一副三角尺不能拼成的角是( )。
A.75° B.105° C.130°
9.把一个平角分成两个角,其中一个角是锐角,另一个角( )。
A.可能是锐角,也可能是钝角 B.可能是直角
C.一定是钝角 D.不确定
二、填空题
10.如图所示,钟面上时针和分针构成的较小角是( )角;分针走一圈,旋转了( )度。
11.如下图,一面镜子反射一条光线。已知∠2=∠3,∠4=140°,那么∠1= 。
12.如图,把两个三角尺叠在一起,已知∠2=40°,那么∠1+∠2+∠3=( )°。
13.下午3时整,钟面上的时针与分针所成的是( )角,下午( )时整,钟面上的时针与分针所成的是平角。
14.下图的射线可以命名为( ),如果这条射线绕点A旋转半周是( )度,旋转一周是( )度。
15.钟面上分针从6走到12形成的角是( )°,分针从9走到12形成的角是( )°,分针从2走到4形成的角是( )°。
16.钟面上( )时整,时针和分针成平角;( )时整或( )时整,钟面上的时针和分针所夹的较小角是30°;钟面上9时整,时针和分针所夹的较小角是( )°。
17.用量角器量出如图中角的度数。
∠1=( ) ∠2=( )
18.钟面9时整时,时针和分针所成的角是( )度,是( )角。( )时整,时针和分针所成的角是平角,是( )度。
三、判断题
19.一个15°的角在放大镜下可能变成30°的角。( )
20.平角的两条边在一条直线上,周角的两条边重合成射线。( )
21.一条长1000米的笔直的公路可以看作是直线。( )
22.角的大小与两边的长短和开口的大小有关。( )
23.一个直角用2倍放大镜看,仍然是一个直角。( )
四、计算题
24.直接写出得数。
4×19= 300×2= 120+80= 25×4=
12亿+38亿= 0×33= 240÷3= 340÷2=
136-36= 70°+20°=
25.求∠1、∠2、∠3各是多少度?
五、作图题
26.量一量∠1、∠2的度数。
六、解答题
27.乐乐发现发射弹珠撞到墙壁后会向另一个方向弹走。
①量出∠1和∠3的度数,说说你的发现。
∠1=( )°,∠2=60°,∠3=( )°,∠4=50°。
我发现:______________________
②下图中发射弹沿箭头方向发出,请你画出它弹走的方向,并判断它是否能够击中砖块A。
28.测量∠1的度数,并通过计算求出∠2的度数(要求有计算过程,写出算式)。
∠1=( )°、∠3=( )、∠2=( )。
29.下面是一张长方形纸折起来形成的图形,已知∠1=30°,∠1比∠2小多少度?
30.量出下面∠1的度数,并在下边空白处画一个60°的角。
∠1=( )°
31.画图。
(1)过一点O,能画直线吗?能画几条?
(2)经过两点A、B,能不能画直线?能画几条?
《四年级暑假新课提升预习练第三单元《角的度量》(含解析)-2024-2025学年下学期小学数学人教版》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 C B C C D C C C C
1.C
【分析】直线是直的,没有端点,无限长,可以向两端无限延长。射线是直的,有1个端点,无限长,可以向一端无限延长。线段是直的,有2个端点,有限长。
【详解】可以两端无限延长的是直线。
故答案为:C
2.B
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,钟面上3:00或9:00,时针和分针之间相差的3个大格数,用大格数3乘30°即可;钟面上4:00,时针和分针之间相差的4个大格数,用大格数4乘30°;钟面上7:00,时针和分针之间相差的5个大格数,用大格数5乘30°;钟面上1:00或11:00,时针和分针之间相差的1个大格数,用大格数1乘30°;依此计算并选择。
【详解】A.3×30°=90°,即3:00和9:00,时针与分针组成的角都是为90°。
B.4×30=120°,即4:00,时针与分针组成的角都是为120°;5×30=150°,即7:00,时针与分针组成的角都是为150°。
C.1×30°=30°,即1:00和11:00,时针与分针组成的角都是为30°。
故答案为:B
【点睛】此题考查了利用钟面上每一大格是30°的性质,来解决分针转动一定的时刻所组成夹角的度数问题的灵活应用能力。
3.C
【分析】钟面上时针走一圈是360°,钟面上有12个大格,所以每个大格是30°。时针1小时走1大格,3小时走3大格。据此可以知道走了多少度。
【详解】走一圈是360°,钟面上有12个大格,所以每个大格是30°。
30°×3=90°
所以,时针走3小时转过的角是90°。
故答案为:C
4.C
【分析】体育课上我们如果向左转或向右转时,就是由原来的方向向左或右旋转90°,即转过的角是直角;如果向后转时,就是由原来的方向向后旋转180°,即转过的角是平角。
【详解】根据分析:体育课上,体育老师让我们向后转时,右脚所转的角应该是一个平角。
故答案为:C
5.D
【分析】A.此图为直角,根据直角的特点,此图的度数等于90°。
B.此图为钝角,根据钝角的特点,此图的度数大于90°小于180°。
C.此图为平角,根据平角的特点,此图的度数等于180°。
D.此图为周角,根据周角的特点,此图的度数等于360°。
【详解】
根据分析,可知上图中度数最大的是。
故答案为:D
【点睛】本题考查的是直角、钝角、平角、周角的特点。
6.C
【分析】一副三角尺上的角有30°、45°、60°、90°,45°-30°=15°,45°+30°=75°,90°+60°=150°,45°+60°=105°,45°+90°=135°,所以用一副三角尺可以画出15°、45°、30°、75°、90°、105°、135°、150°的角,据此即可解答。
【详解】用一副三角尺可以拼出75°、15°、150°的角。
故答案为:C。
7.C
【分析】钟表上共有12个大格,每个大格是30°,90°的角需要分针与时针之间有3个大格,在3点或9点的时间恰好成90°,据此结合选项进行选择即可。
【详解】A.2时时,分针与时针之间有2个大格,时针、分针成60°角;
B.6时时,分针与时针之间有6个大格,时针、分针成180°角;
C.9时时,分针与时针之间有3个大格,时针、分针成90°角;
D.4时时,分针与时针之间有4个大格,时针、分针成120°角。
故答案为:C
【点睛】本题主要依据平时的留心观察发现,结合钟表的构造即可解答。
8.C
【分析】一副三角板中的各个角的度数分别是30°、60°、45°、90°。将它们进行组合,可得到的角有60°-45°=15°,60°+45°=105°,60°+90°=150°,90°+45°=135°,90°+30°=120°,30°+45°=75°。据此解答。
【详解】A.30°+45°=75°,用一副三角尺可以拼成75°的角;
B.60°+45°=105°,用一副三角尺可以拼成105°的角;
C.用一副三角尺不能拼成130°的角;
故答案为:C
9.C
【分析】平角是180°的角,锐角是大于0°且小于90°的角,直角是等于90°的角,钝角是大于90°且小于180°的角。据此解答。
【详解】根据分析可知:平角是180°的角,把一个平角分成两个角,其中一个角是锐角,由于锐角是小于90°的角,180°的角减去一个小于90°的角,得到的另一个角肯定是大于90°且小于180°的角,所以另一个角一定是一个钝角。
故答案为:C
10. 锐 360
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°;2时整,时针和分针之间有2个大格,所形成的较小角是2乘30°,小于90°的角为锐角;分针走一圈,旋转了1周,也就是360°;据此解答。
【详解】根据分析:2×30°=60°,60°<90°,60°为锐角,所以钟面上时针和分针构成的较小角是锐角;分针走一圈,旋转了360度。
11.100°/100度
【分析】根据题意可知∠1、∠2和∠3组成一个平角,∠1与∠2组成∠4,∠3与∠4组成一个平角,平角的度数是180°,用180°减去∠4的度数就是∠3的度数,∠2=∠3,那么再用∠4的度数减去∠2的度数即可求出∠1。
【详解】∠3:180°-∠4
=180°-140°
=40°
∠2=∠3=40°
∠1:∠4-∠2
=140°-40°
=100°
12.140
【分析】由题图可知,∠2和∠3组成三角尺的直角,即∠3=90°-∠2;∠2和∠1组成另一个三角尺的直角,即∠1=90°-∠2;又已知∠2=40°,所以可以分别求出∠3和∠1的度数,然后再把∠1、∠2和∠3这三角的度数相加,即可解答。
【详解】因为∠2=40°
∠2+∠3=90°
所以∠3=90°-∠2
=90°-40°
=50°
因为∠2=40°
∠2+∠1=90°
所以∠1=90°-∠2
=90°-40°
=50°
∠1+∠2+∠3=40°+50°+50°
=90°+50°
=140°
即如题图,把两个三角尺叠在一起,已知∠2=40°,那么∠1+∠2+∠3=140°。
13. 直 6
【分析】平角:射线OA绕着点O旋转,当终止位置OC和起始位置OA成一直线时,所成的角叫做平角。平角为180度。
直角:平角的一半叫做直角。直角为90度。
【详解】下午3时整,时针指向3,分针指向12,夹角为90度,时针与分针所成的是直角;
下午6时整,时针指向6,分针指向12,夹角为180度,时针与分针所成的是平角。
14. 射线AB 180 360
【分析】射线命名时,以端点开始,然后和射线上任意另一个点组合起来命名;
一条射线绕端点旋转半周,形成一个平角,平角的度数为180度;如果绕端点旋转一周,形成一个周角,周角的度数为360度。
【详解】这条射线可以命名为:射线AB;
这条射线绕点A旋转半周是一个平角,是180度,若旋转一周是一个周角,是360度。
15. 180 90 60
【分析】钟面一周为360°,被平均分成12个大格,每个大格对应30°。分针每走一个大格形成的角度为30°,用分针走的大格数×30°即可;钟面上分针从6走到12共走了6大格,用6×30°即可计算出钟面上分针从6走到12形成的角;分针从9走到12共走了3大格,用3×30°即可计算出钟面上分针从9走到12形成的角;分针从2走到4共走了2大格,用2×30°即可计算出钟面上分针从2走到4形成的角,据此解题。
【详解】(12-6)×30°
=6×30°
=180°
(12-9)×30°
=3×30°
=90°
(4-2)×30°
=2×30°
=60°
钟面上分针从6走到12形成的角是180°,分针从9走到12形成的角是90°,分针从2走到4形成的角是60°。
16. 6 11 1 90
【分析】钟面上有12大格,把钟面平均分成12等份,每一大格对应的夹角是30°;6时整,分针指向12,时针指向6,时针与分针在一条直线,时针和分针成平角;当11时整或1时整,时针与分针所夹的较小角正好对应一大格,是30°;钟面上9时整,时针和分针所夹的较小角正对应3大格,是30°×3=90°;据此即可解答。
【详解】根据分析可知,钟面上6时整,时针和分针成平角;11时整或1时整,钟面上的时针和分针所夹的较小角是30°;钟面上9时整,时针和分针所夹的较小角是90°。
17. 135°/135度 75°/75度
【分析】用量角器的圆点和角的顶点重合,0刻度线和角的一条边重合,另一条边在量角器上的刻度就是该角的度数,据此解答。
【详解】测量结果如下:
【点睛】本题主要考查了学生正确使用量角器测量角的能力。
18. 90 直 6 180
【分析】在9时整时,时针指向9,分针指向12,钟面上一个大格的度数为30度,所以时针与分针之间有3个大格,30×3=90(度),等于90度的角叫做直角;
等于180度的角叫做平角,整时,分针指向12,当时针指向6时,时针与分针之间有6个大格,是30×6=180(度),由此进行解答即可。
【详解】30×3=90(度)
30×6=180(度)
钟面9时整时,时针和分针所成的角是90度,是直角。6时整,时针和分针所成的角是平角,是180度。
【点睛】此题考查了钟面的认识以及角的分类,解答此题,要掌握钟面上每一大格的角度是30度。
19.×
【分析】角的大小与两边的长短无关,只与边叉开的大小有关,用放大镜看角时,放大的是角的边的长度,不改变角的形状,即边叉开的大小不变,所以用放大镜看角,角的大小不变。
【详解】根据分析可知:一个15°的角在放大镜下度数不变,原题说法错误。
故答案为:×
20.√
【分析】一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。平角的特点是两条边成一条直线;一条射线绕着它的端点旋转一周所形成的角,叫做周角。周角的特点是两条边重合成射线。据此解答。
【详解】平角的两条边在一条直线上,周角的两条边重合成射线。原题说法正确。
故答案为:√
21.×
【分析】根据直线的含义:直线没有端点,无限延长,连接两点的线段的长度叫做两点间的距离。据此判断即可。
【详解】一条长1000米的笔直的公路可以看作是线段。所以原题说法错误。
故答案为:×
22.×
【分析】从一点引出两条射线所组成的图形叫做角。角的两条边是射线,射线可以无限延伸。角的大小是指角两条边所张开的大小。根据角的组成和角的大小定义,即可解答。
【详解】根据角的含义可知,角的大小与角两边的长短无关,与角的两边叉开的大小有关,开叉越大,角就越大,反之越小,原说法错误。
故答案为:×
【点睛】正确理解角的定义,明确角的大小与角两边的长短无关,与角的两边叉开的大小有关,是解答此题的关键。
23.√
【分析】用2倍放大镜看角,只改变角两边的长度,角两边的开叉的大小不变,即角的度数不变。
【详解】一个直角用2倍放大镜看,仍然是一个直角。
故答案为:√
24.76;600;200;100;
50亿;0;80;170;
100;90°
【详解】略
25.∠1=35°;∠2=35°;∠3=55°
【分析】观察图中可知,∠1和145°角组成平角,平角=180°,因此用180°减去145°即可求出∠1的度数;∠2和145°角组成平角,因此用180°减去145°即可求出∠2的度数;∠1和∠3组成直角,直角=90°,因此用90°减去∠1的度数即可求出∠3的度数。
【详解】∠1=180°-145°=35°
∠2=180°-145°=35°
∠3=90°-35°=55°
26.∠1=60°,∠2=120°
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量即可。
【详解】根据测量可知,∠1=60°,∠2=120°。
【点睛】熟练掌握角的度量方法,是解答此题的关键。
27.(1)60;50;见详解
(2)见详解;不能
【分析】(1)根据角的度量方法:量角要注意两对齐:量角器的中心和角的顶点对齐;量角器的0刻度线和角的一条边对齐;做到两对齐后看角的另一条边对着刻度线几,这个角就是几度;看刻度要分清内外圈。比较∠1和∠2、∠3和∠4,得出发射弹沿箭头发出的射线与墙壁的角度与弹珠撞到墙壁后弹出去的射线与墙壁的角度的关系。
(2)根据发射弹沿箭头发出的射线与墙壁的角度等于弹珠撞到墙壁后弹出去的射线与墙壁的角度的关系画图即可。
【详解】①量出∠1和∠3的度数,说说你的发现。
∠1=60°,∠2=60°,∠3=50°,∠4=50°。
我发现:发射弹沿箭头发出的射线与墙壁的角度等于弹珠撞到墙壁后弹出去的射线与墙壁的角度。
②下图中发射弹沿箭头方向发出,发射弹沿箭头发出的射线与墙壁的角度等于弹珠撞到墙壁后弹出去的射线与墙壁的角度,画出图如下:
它不能击中砖块A。
28.120;60°;30°
计算过程见详解
【分析】量角器的使用方法。两合一看,两合是指中心点与角的顶点重合;0刻度线与角的一边重合。一看就是要看角的另一边所对的量角器的刻度。看角的度数时要注意是看外刻度还是内刻度。角的开口向左看外刻度线,角的开口向右看内刻度线。
根据角的度量方法,测量∠1的度数,然后根据∠1+∠3=180°,∠3=180°-∠1;∠3+∠2=90°,∠2=90°-∠3。据此解答。
【详解】测量可知∠1=120°。
∠3=180°-∠1=180°-120°=60°
∠2=90°-∠3=90°-60°=30°。
即∠1=120°、∠3=60°、∠2=30°。
29.45度
【分析】
根据题意可知,∠2=∠3,平角是180°,∠2和∠3和∠1构成一个平角,据此用180°减去∠1然后再除以2,即可求出∠2的度数,然后据此进行解题。
【详解】180-30=150(度)
150÷2=75(度)
75-30=45(度)
答:∠1比∠2小45度。
30.105;
图见详解
【分析】量角的步骤是:先把量角器的中心与角的顶点重合,0刻度线与角的一条边重合,角的另一边所对的量角器上的刻度,就是这个角的度数,依此测量即可。
画角的步骤是:先画一条射线,使量角器的中心和射线的端点重合,0刻度线和射线重合,然后在量角器相对应的刻度线的地方点一个点,最后以画出的射线的端点为端点,通过刚画的点,再画一条射线;依此画图即可。
【详解】根据分析可量出∠1的度数,∠1=105°;画出60°的角。如图:
31.(1)能,无数条;(2)能,一条。
【分析】根据直线的性质:同一平面内,两点确定一条直线,过一点能画无数条直线;据此解答即可。
【详解】(1)根据直线的性质可知:过一点O,能画直线,且能画无数条。
(2)经过两点A、B,能画直线,且只能画一条。
【点睛】本题主要考查的是直线的性质,解题关键在于熟知概念。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
