人教版九年级数学上册24.1.4.2 圆内接四边形课件(共16张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.4.2 圆内接四边形课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 541.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 15:49:14 | ||
图片预览



文档简介
(共16张PPT)
第24章 圆
24.1.4.2
圆内接四边形
授课:
时间:
问题回顾
(1) 什么是圆心角 什么是圆周角?
顶点在圆心的角是圆心角.
顶点在圆上, 并且两边都与圆相交的角叫做圆周角.
(2) 同弧或等弧所对的圆心角和圆周角有什么关系?
(3) 同弧或等弧所对的圆周角之间有什么关系?
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理推论:同弧或等弧所对的圆周角相等.
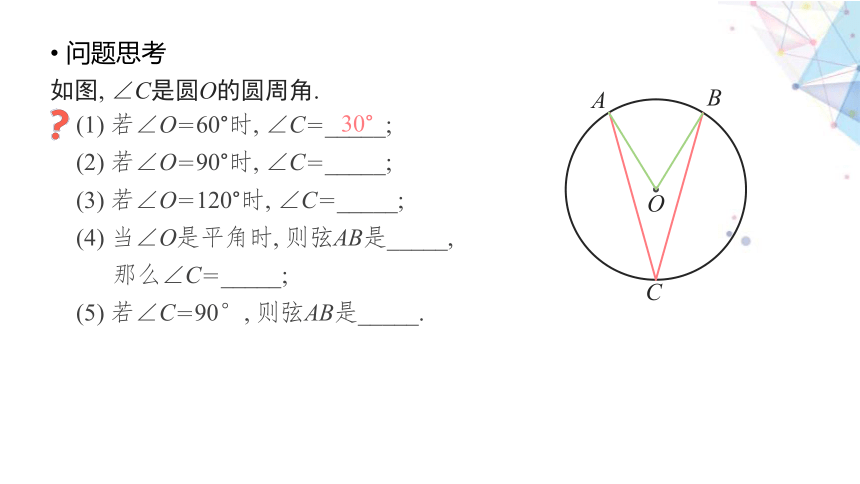
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
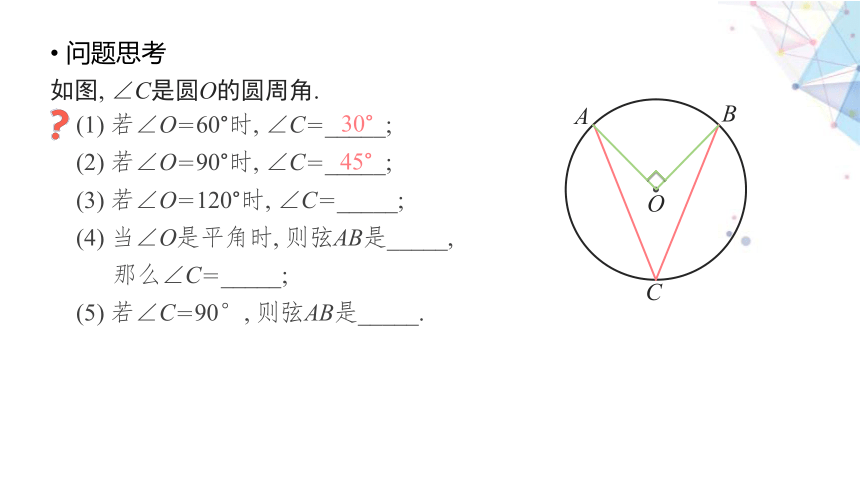
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
45°
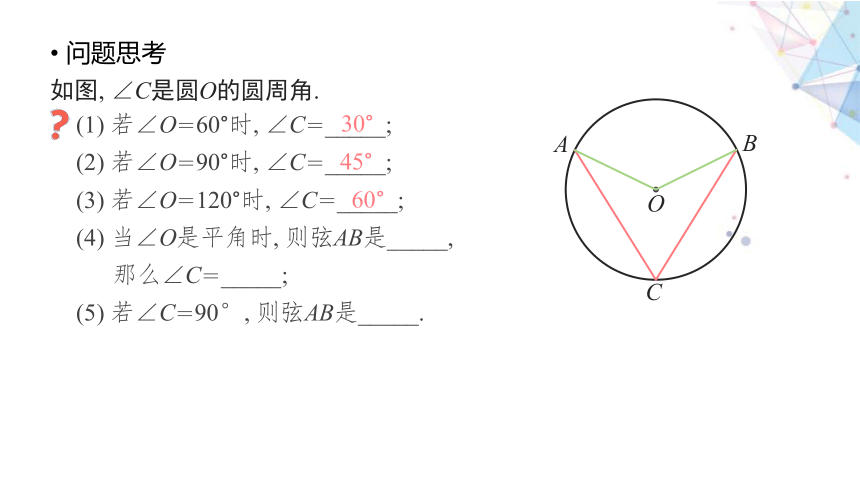
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
45°
60°
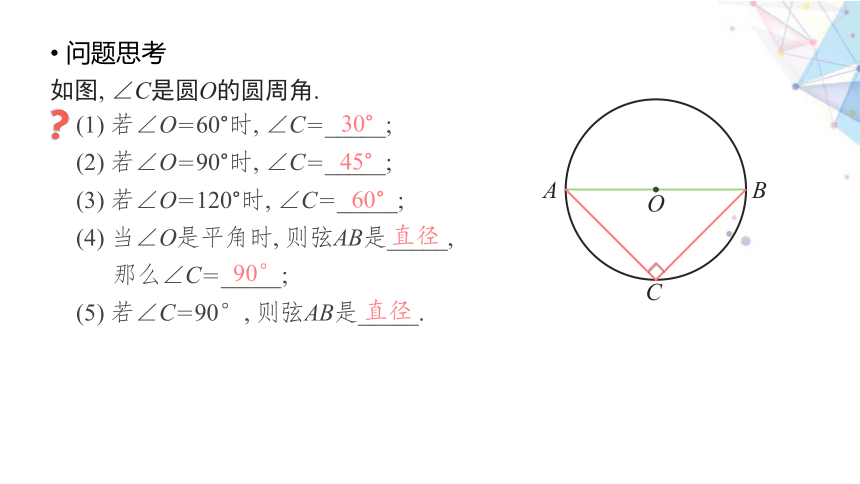
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
45°
60°
直径
90°
直径
得出结论
圆周角定理推论2:
半圆或直径所对的圆周角是直角, 90°的圆周角所对的弦是直径.
符号语言:
∵AB是直径,
∴∠C=90°.
C
A
B
O
∵∠C=90°,
∴ AB是直径.
符号语言:
典例精析
例1.如图, 圆O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交圆O于点D.
(1) ∠ACB=____,∠ADB=____;
(2) 由∠ACB的平分线可以推出=____;
(3) 如何求BC,AD,BD的长呢
90°
90°
解: ∵AB是直径, ∴∠ACB=∠ADB=90°,
∴BC=cm,
连接OD,∵CD平分∠ACB,
∴∠ACD=∠DCB, ∠AOD=∠BOD,
∴AD=BD,
∵AD2+BD2=AB2,
∴AD=BD=AB=5cm.
圆周角相等不能直接推出所对的弦相等.
小试锋芒
练习1.如图, ⊙O是△ABC的外接圆, AC是⊙O的直径, 点P在⊙O上.若∠ACB=40°, 则∠BPC的度数为( ).
A. 40° B. 45° C. 50° D. 55°
C
小试锋芒
练习2.已知: 如图, AB为⊙O的直径, AB=AC, BC交⊙O于点D, AC交⊙O于点E, ∠BAC=45°.
(1)求∠EBC的度数;
(2)求证: BD=CD.
答案: (1)∠EBC=22.5°;
(2)连接AD,根据等腰三角形三线合一即可证明.
问题探索
如图, AB是圆O的弦, ∠AOB=130°,点P是圆上的点.
P
A
B
O
(1) 弦AB所对的弧是_________;
(2) 当点P在优弧时, ∠APB=_____;
(3) 当点P’在劣弧时, ∠AP’B=_____;
(4) 若角∠AOB=α,则∠APB=___________;
(5) 思考∠APB与∠AP’B的数量关系.
,
P’
65°
115°
或
∠APB+∠AP’B=180°
探索新知
如果一个多边形的所有顶点都在同一个圆上, 这个多边形叫做圆内接多边形.
这个圆叫做多边形的外接圆.
D
A
C
O
B
例如: 四边形ABCD是圆O的内接四边形, 圆O是四边形ABCD的外接圆.
圆内接四边形的四个角之间有什么关系
∠A+∠C=180°,
∠B+∠D=180°.
得出结论
圆内接四边形对角互补.
符号语言:
∵ABCD是圆O的内接四边形,
∴∠A+∠C=180°, ∠B+∠D=180°.
D
A
C
O
B
练习2.如图, 四边形ABCD内接于⊙O, 若∠B=128°, 则∠D的大小为( ).
A. 42° B. 52°
C. 62° D. 72°
B
典例精析
例2.如图, 四边形ABCD是圆的内接四边形, ∠A=60°, ∠B=90°, AB=2,
CD=1, 求AD的长.
解: 延长AD, BC交于点E,
∵ABCD是圆的内接四边形,
∴∠ADC=∠CDE=180°-90°=90°,
∴∠E=30°,
∴CE=2CD=2,AE=2AB=4,
在Rt△CDE中, DE=,
∴AD=4-.
小试锋芒
练习3.如图, 在△ABC中, AC=BC, D是AB上一点, ⊙O经过点A, C, D, 交BC于点E, 过点D作DF//BC, 交⊙O于点F, 连接AF, EF, CF.
求证: (1)四边形DBCF是平行四边形;
(2)AF=EF.
谢 谢 观 看
第24章 圆
24.1.4.2
圆内接四边形
授课:
时间:
问题回顾
(1) 什么是圆心角 什么是圆周角?
顶点在圆心的角是圆心角.
顶点在圆上, 并且两边都与圆相交的角叫做圆周角.
(2) 同弧或等弧所对的圆心角和圆周角有什么关系?
(3) 同弧或等弧所对的圆周角之间有什么关系?
圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理推论:同弧或等弧所对的圆周角相等.
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
45°
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
45°
60°
问题思考
C
A
B
O
如图, ∠C是圆O的圆周角.
(1) 若∠O=60°时, ∠C=_____;
(2) 若∠O=90°时, ∠C=_____;
(3) 若∠O=120°时, ∠C=_____;
(4) 当∠O是平角时, 则弦AB是_____,
那么∠C=_____;
(5) 若∠C=90°, 则弦AB是_____.
30°
45°
60°
直径
90°
直径
得出结论
圆周角定理推论2:
半圆或直径所对的圆周角是直角, 90°的圆周角所对的弦是直径.
符号语言:
∵AB是直径,
∴∠C=90°.
C
A
B
O
∵∠C=90°,
∴ AB是直径.
符号语言:
典例精析
例1.如图, 圆O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交圆O于点D.
(1) ∠ACB=____,∠ADB=____;
(2) 由∠ACB的平分线可以推出=____;
(3) 如何求BC,AD,BD的长呢
90°
90°
解: ∵AB是直径, ∴∠ACB=∠ADB=90°,
∴BC=cm,
连接OD,∵CD平分∠ACB,
∴∠ACD=∠DCB, ∠AOD=∠BOD,
∴AD=BD,
∵AD2+BD2=AB2,
∴AD=BD=AB=5cm.
圆周角相等不能直接推出所对的弦相等.
小试锋芒
练习1.如图, ⊙O是△ABC的外接圆, AC是⊙O的直径, 点P在⊙O上.若∠ACB=40°, 则∠BPC的度数为( ).
A. 40° B. 45° C. 50° D. 55°
C
小试锋芒
练习2.已知: 如图, AB为⊙O的直径, AB=AC, BC交⊙O于点D, AC交⊙O于点E, ∠BAC=45°.
(1)求∠EBC的度数;
(2)求证: BD=CD.
答案: (1)∠EBC=22.5°;
(2)连接AD,根据等腰三角形三线合一即可证明.
问题探索
如图, AB是圆O的弦, ∠AOB=130°,点P是圆上的点.
P
A
B
O
(1) 弦AB所对的弧是_________;
(2) 当点P在优弧时, ∠APB=_____;
(3) 当点P’在劣弧时, ∠AP’B=_____;
(4) 若角∠AOB=α,则∠APB=___________;
(5) 思考∠APB与∠AP’B的数量关系.
,
P’
65°
115°
或
∠APB+∠AP’B=180°
探索新知
如果一个多边形的所有顶点都在同一个圆上, 这个多边形叫做圆内接多边形.
这个圆叫做多边形的外接圆.
D
A
C
O
B
例如: 四边形ABCD是圆O的内接四边形, 圆O是四边形ABCD的外接圆.
圆内接四边形的四个角之间有什么关系
∠A+∠C=180°,
∠B+∠D=180°.
得出结论
圆内接四边形对角互补.
符号语言:
∵ABCD是圆O的内接四边形,
∴∠A+∠C=180°, ∠B+∠D=180°.
D
A
C
O
B
练习2.如图, 四边形ABCD内接于⊙O, 若∠B=128°, 则∠D的大小为( ).
A. 42° B. 52°
C. 62° D. 72°
B
典例精析
例2.如图, 四边形ABCD是圆的内接四边形, ∠A=60°, ∠B=90°, AB=2,
CD=1, 求AD的长.
解: 延长AD, BC交于点E,
∵ABCD是圆的内接四边形,
∴∠ADC=∠CDE=180°-90°=90°,
∴∠E=30°,
∴CE=2CD=2,AE=2AB=4,
在Rt△CDE中, DE=,
∴AD=4-.
小试锋芒
练习3.如图, 在△ABC中, AC=BC, D是AB上一点, ⊙O经过点A, C, D, 交BC于点E, 过点D作DF//BC, 交⊙O于点F, 连接AF, EF, CF.
求证: (1)四边形DBCF是平行四边形;
(2)AF=EF.
谢 谢 观 看
同课章节目录
