人教版九年级数学上册25.3 用频率估计概率课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学上册25.3 用频率估计概率课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 16:33:47 | ||
图片预览




文档简介
(共18张PPT)
第25章 概率初步
25.3
用频率估计概率
授课:
时间:
问题思考
(1) 抛一枚硬币, 会有几种可能
(2) 正面朝上和反面朝上的概率是多少
2种, 分别是正面朝上、反面朝上.
P(正面朝上) = ,
(3) 如果上抛500次, 向上的次数会是250吗
P(反面朝上) = .
小雯: 实践才能出真知!
小组活动
全班同学分成10组, 每组同学抛掷一枚均匀硬币50次, 记录 “正面朝上”的次数, 并算出“正面朝上”的频率, 完成下表:
各小组统计情况 第1小组 第2小组 第3小组 … 第10小组
“正面朝上”的频数
“正面朝上”的频率
探索新知
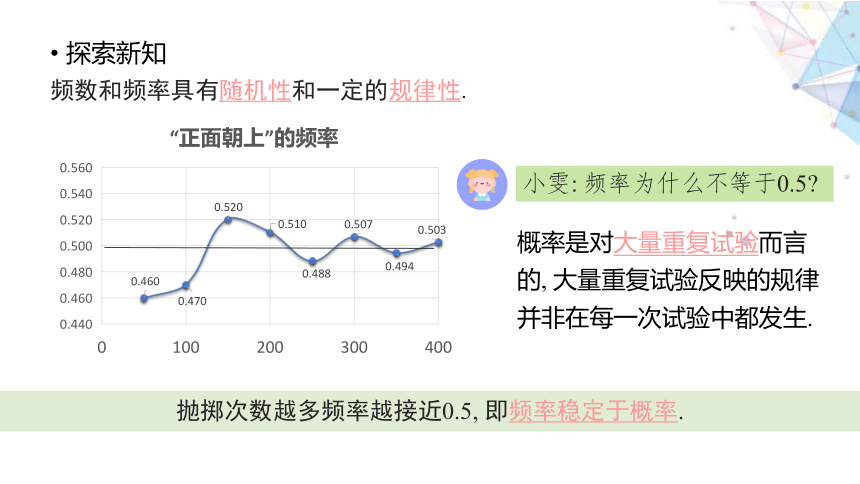
频数和频率具有随机性和一定的规律性.
小雯: 频率为什么不等于0.5
概率是对大量重复试验而言的, 大量重复试验反映的规律并非在每一次试验中都发生.
抛掷次数越多频率越接近0.5, 即频率稳定于概率.
鉴往知来
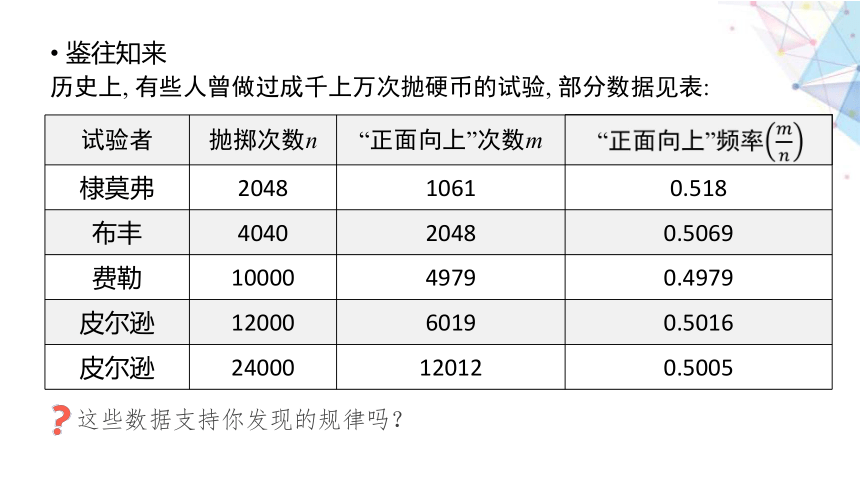
历史上, 有些人曾做过成千上万次抛硬币的试验, 部分数据见表:
试验者 抛掷次数n “正面向上”次数m “正面向上”频率
棣莫弗 2048 1061 0.518
布丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
这些数据支持你发现的规律吗?
问题思考
抛硬币的事件属于古典概型, 可能出现的结果有限, 每种结果出现的可能性相等.
如右图, 抛掷一枚图钉, 针尖朝上的概率是多少呢
抛掷图钉是一个随机事件, 可能出现的结果我们无法用列举法求其概率.
小智:通过多次试验, 用频率估计概率.
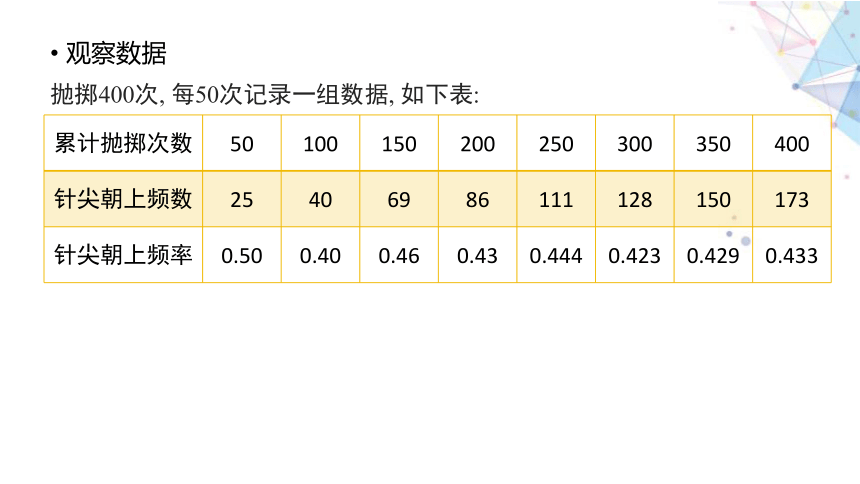
观察数据
累计抛掷次数 50 100 150 200 250 300 350 400
针尖朝上频数 25 40 69 86 111 128 150 173
针尖朝上频率 0.50 0.40 0.46 0.43 0.444 0.423 0.429 0.433
抛掷400次, 每50次记录一组数据, 如下表:
观察数据
根据实验数据绘制频数趋势图:
在抛掷图钉试验中, “针尖朝上”的频率随着试验次数的增加, 稳定在常数0.435附近.
∴P(针尖朝上) ≈ 0.435.
归纳总结
试验次数越多频率越接近概率, 即频率稳定于概率.
通过大量重复试验, 可以用随机事件发生的频率来估计该事件发生的概率.
鉴往知来
雅各布·伯努利
概率论的先驱之一.
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.
这称为大数法则,亦称大数定律.
一般地, 在大量重复的n次试验中,随机事件A发生的次数为m,
若随机事件A发生的频率会稳定到某个常数p,则这个常数可以估计事件A发生的概率, 即
P(A) = p.
明察秋毫
练习1.下列说法正确的是____(填序号).
连续掷一枚质地均匀硬币10次, 结果10次全部是正面, 则正面向上的概率是1;
掷硬币10000次, 则正面向上的频率在0.5附近;
某转盘一等奖的中奖率为1%, 则转动100次一定能中一等奖;
设一大批灯泡的次品率为0.01, 那么从中抽取1000只灯泡, 一定有10只次品.
②
典例精析
某林业部门要考察某种幼苗在一定条件下的移植成活率.
应采用怎样的做法
典例精析
例1.某林业部门要考察某种幼苗在一定条件下的移植成活率.
分析: 幼苗成活或不成活两种结果可能性未知, 所以成活率要由频率去估计.
统计成活频数(m株)
用频率估计成活率
计算成活的频率
越来越稳定
在同等情况下, 对大量幼苗(n株)进行移植.
典例精析
例1.某林业部门要考察某种幼苗在一定条件下的移植成活率.
移植总数n 成活数m 成活频率
10 8 0.800
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
(1) 补全表格;
(2) 估算幼苗的成活率.
随着移植树的增加, 幼苗移植的成活频率稳定于0.9.
∴幼苗的成活率约90%.
0.940
0.923
0.883
0.905
0.897
(3) 若移植10万株幼苗, 则预估会成活多
少株
10 × 90% ≈ 9(万株),
∴预计会成活9万株.
小试锋芒
练习2.一个不透明的盒子中装有10个黑球和若干个白球, 它们除颜色不同外, 其余均相同.从盒子中随机摸出一球记下其颜色, 再把它放回盒子中摇匀, 重复上述过程, 共试验400次, 其中有240次摸到白球.由此估计盒子中的白球大约有( ).
A. 10个 B. 15个 C. 18个 D. 30个
B
小试锋芒
练习3.水果公司进价2元/kg购进10000kg柑橘, 水果公司想出售这批柑橘获得5000元利润.
若运输中无损坏的柑橘, 应如何定价
由于柑橘在运输中有损坏, 补全表格,
估计柑橘的损坏率, 应如何定价
柑橘总质量() 损坏柑橘质量() 柑橘损坏频率
(精确到0.001)
100 10.5 0.105
200 19.42
300 30.39
400 39.24 0.098
500 51.54
解: (1)设定价为 元/ .
10000( 2)=5000,
解得 =2.5,
∴定价应为2.5元/ .
小试锋芒
(2) 由于柑橘在运输中有损坏, 补全表格, 估计柑橘的损坏率, 应如何定价
柑橘总质量() 损坏柑橘质量() 柑橘损坏频率
(精确到0.001)
100 10.5 0.105
200 19.42
300 30.39
400 39.24 0.098
500 51.54
0.097
0.101
0.103
解: 随着柑橘总质量的增加,柑橘损坏
频率稳定于0.1.
∴柑橘损坏率约10%.
设定价为y元/kg.
10000·(1-10%)· 20000=5000,
解得 ≈ 2.78,
∴定价约2.78元/kg.
谢 谢 观 看
第25章 概率初步
25.3
用频率估计概率
授课:
时间:
问题思考
(1) 抛一枚硬币, 会有几种可能
(2) 正面朝上和反面朝上的概率是多少
2种, 分别是正面朝上、反面朝上.
P(正面朝上) = ,
(3) 如果上抛500次, 向上的次数会是250吗
P(反面朝上) = .
小雯: 实践才能出真知!
小组活动
全班同学分成10组, 每组同学抛掷一枚均匀硬币50次, 记录 “正面朝上”的次数, 并算出“正面朝上”的频率, 完成下表:
各小组统计情况 第1小组 第2小组 第3小组 … 第10小组
“正面朝上”的频数
“正面朝上”的频率
探索新知
频数和频率具有随机性和一定的规律性.
小雯: 频率为什么不等于0.5
概率是对大量重复试验而言的, 大量重复试验反映的规律并非在每一次试验中都发生.
抛掷次数越多频率越接近0.5, 即频率稳定于概率.
鉴往知来
历史上, 有些人曾做过成千上万次抛硬币的试验, 部分数据见表:
试验者 抛掷次数n “正面向上”次数m “正面向上”频率
棣莫弗 2048 1061 0.518
布丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
这些数据支持你发现的规律吗?
问题思考
抛硬币的事件属于古典概型, 可能出现的结果有限, 每种结果出现的可能性相等.
如右图, 抛掷一枚图钉, 针尖朝上的概率是多少呢
抛掷图钉是一个随机事件, 可能出现的结果我们无法用列举法求其概率.
小智:通过多次试验, 用频率估计概率.
观察数据
累计抛掷次数 50 100 150 200 250 300 350 400
针尖朝上频数 25 40 69 86 111 128 150 173
针尖朝上频率 0.50 0.40 0.46 0.43 0.444 0.423 0.429 0.433
抛掷400次, 每50次记录一组数据, 如下表:
观察数据
根据实验数据绘制频数趋势图:
在抛掷图钉试验中, “针尖朝上”的频率随着试验次数的增加, 稳定在常数0.435附近.
∴P(针尖朝上) ≈ 0.435.
归纳总结
试验次数越多频率越接近概率, 即频率稳定于概率.
通过大量重复试验, 可以用随机事件发生的频率来估计该事件发生的概率.
鉴往知来
雅各布·伯努利
概率论的先驱之一.
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.
这称为大数法则,亦称大数定律.
一般地, 在大量重复的n次试验中,随机事件A发生的次数为m,
若随机事件A发生的频率会稳定到某个常数p,则这个常数可以估计事件A发生的概率, 即
P(A) = p.
明察秋毫
练习1.下列说法正确的是____(填序号).
连续掷一枚质地均匀硬币10次, 结果10次全部是正面, 则正面向上的概率是1;
掷硬币10000次, 则正面向上的频率在0.5附近;
某转盘一等奖的中奖率为1%, 则转动100次一定能中一等奖;
设一大批灯泡的次品率为0.01, 那么从中抽取1000只灯泡, 一定有10只次品.
②
典例精析
某林业部门要考察某种幼苗在一定条件下的移植成活率.
应采用怎样的做法
典例精析
例1.某林业部门要考察某种幼苗在一定条件下的移植成活率.
分析: 幼苗成活或不成活两种结果可能性未知, 所以成活率要由频率去估计.
统计成活频数(m株)
用频率估计成活率
计算成活的频率
越来越稳定
在同等情况下, 对大量幼苗(n株)进行移植.
典例精析
例1.某林业部门要考察某种幼苗在一定条件下的移植成活率.
移植总数n 成活数m 成活频率
10 8 0.800
50 47
270 235 0.870
400 369
750 662
1500 1335 0.890
3500 3203 0.915
7000 6335
9000 8073
14000 12628 0.902
(1) 补全表格;
(2) 估算幼苗的成活率.
随着移植树的增加, 幼苗移植的成活频率稳定于0.9.
∴幼苗的成活率约90%.
0.940
0.923
0.883
0.905
0.897
(3) 若移植10万株幼苗, 则预估会成活多
少株
10 × 90% ≈ 9(万株),
∴预计会成活9万株.
小试锋芒
练习2.一个不透明的盒子中装有10个黑球和若干个白球, 它们除颜色不同外, 其余均相同.从盒子中随机摸出一球记下其颜色, 再把它放回盒子中摇匀, 重复上述过程, 共试验400次, 其中有240次摸到白球.由此估计盒子中的白球大约有( ).
A. 10个 B. 15个 C. 18个 D. 30个
B
小试锋芒
练习3.水果公司进价2元/kg购进10000kg柑橘, 水果公司想出售这批柑橘获得5000元利润.
若运输中无损坏的柑橘, 应如何定价
由于柑橘在运输中有损坏, 补全表格,
估计柑橘的损坏率, 应如何定价
柑橘总质量() 损坏柑橘质量() 柑橘损坏频率
(精确到0.001)
100 10.5 0.105
200 19.42
300 30.39
400 39.24 0.098
500 51.54
解: (1)设定价为 元/ .
10000( 2)=5000,
解得 =2.5,
∴定价应为2.5元/ .
小试锋芒
(2) 由于柑橘在运输中有损坏, 补全表格, 估计柑橘的损坏率, 应如何定价
柑橘总质量() 损坏柑橘质量() 柑橘损坏频率
(精确到0.001)
100 10.5 0.105
200 19.42
300 30.39
400 39.24 0.098
500 51.54
0.097
0.101
0.103
解: 随着柑橘总质量的增加,柑橘损坏
频率稳定于0.1.
∴柑橘损坏率约10%.
设定价为y元/kg.
10000·(1-10%)· 20000=5000,
解得 ≈ 2.78,
∴定价约2.78元/kg.
谢 谢 观 看
同课章节目录
