26.1.1 反比例函数 课件(共16张PPT) 数学人教版九年级下册
文档属性
| 名称 | 26.1.1 反比例函数 课件(共16张PPT) 数学人教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第26章 反比例函数
26.1.1
反比例函数
授课:
时间:
问题思考
观察动图, 你能得出怎样的实验现象
实验现象:
①用一根铁钉去扎气球时, 气球立马就炸了;
②用一堆铁钉“齐心协力”去扎气球时, 气球却显得格外的坚硬, 怎么样的都扎不破.
你能解释这是什么原因吗
问题思考
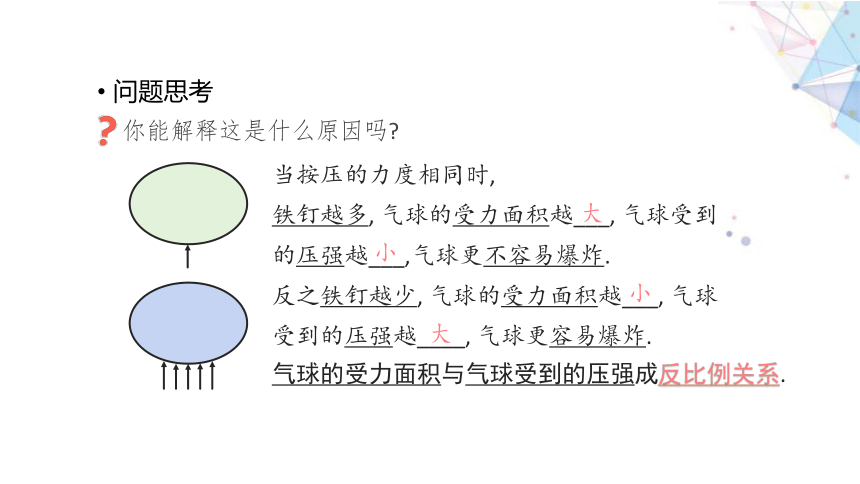
你能解释这是什么原因吗
当按压的力度相同时,
铁钉越多, 气球的受力面积越___, 气球受到的压强越___,气球更不容易爆炸.
反之铁钉越少, 气球的受力面积越___, 气球受到的压强越____, 气球更容易爆炸.
大
小
小
大
气球的受力面积与气球受到的压强成反比例关系.
问题思考
下列问题中, 变量间具有函数关系吗 如果有, 写出函数解析式.
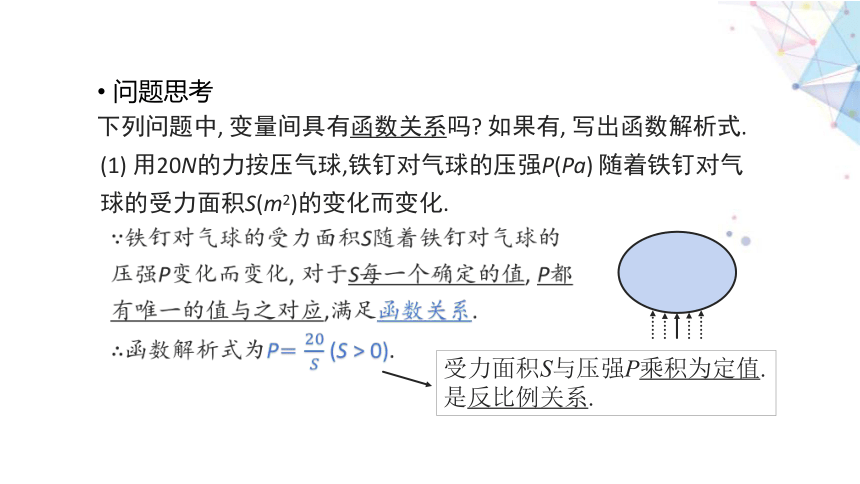
(1) 用20N的力按压气球,铁钉对气球的压强P(Pa) 随着铁钉对气球的受力面积S(m2)的变化而变化.
∵铁钉对气球的受力面积S随着铁钉对气球的压强P变化而变化, 对于S每一个确定的值, P都有唯一的值与之对应,满足函数关系.
∴函数解析式为P= (S > 0).
受力面积S与压强P乘积为定值.
是反比例关系.
问题思考
下列问题中, 变量间具有函数关系吗 如果有, 写出函数解析式.
(2) 昌赣高速铁路全程为416km, 某次列车的平均速度v (km/h)随此次列车的全程运行时间t (h)的变化而变化;
∵列车的平均速度v随着列车的全程运行时间t变化而变化, 对于t每一个确定的值, v都有唯一的值与之对应,满足函数关系.
∴函数解析式为v= (t > 0).
时间t与速度v乘积为定值, 是反比例关系.
问题思考
下列问题中, 变量间具有函数关系吗 如果有, 写出函数解析式.
(3) 已知北京市的总面积为1.64×104 2 , 人均占有面积 (单位: 2/人) 随全市总人口n(单位:人) 的变化而变化.
∵人均占有面积 随着全市总人口n变化而变化, 对于n每一个确定的值, S都有唯一的值与之对应,满足函数关系.
∴函数解析式为S= (n > 0).
总人口n与人均占有面积S乘积为定值, 是反比例关系.
观察思考
P= ,
v= ,
S= .
观察这些函数解析式, 它们有什么共同特征
共同特征: 都是形如的形式.
一般地,形如 (k是常数, )的函数称为反比例函数.
自变量, x≠0
因变量, y≠0
比例系数, k≠0
明察秋毫
练习1. 下列函数是反比例函数的是________.
①; ② ; ③; ④;
⑤; ⑥ ; ⑦; ⑧.
③⑦⑧
反比例函数的三种表达方式(k为常数, k≠0):
, , .
小试锋芒
练习2.用函数解析式表示下列问题中变量间的对应关系:
(1)某住宅小区要种植一块面积为1000m2 的矩形草坪, 草坪的长y(单位:m) 随宽x(单位:m)的变化而变化;
(2)一个游泳池的容积为2000m3, 游泳池注满水所用时间t(单位:h)随注水速度v(单位: m3/h)的变化而变化;
(3)某长方体的体积为1000cm3, 长方体的高h (单位:cm)随底面积S(单位: cm2)的变化而变化.
答案: (1) ; (2); (3).
问题思考
反比例关系和反比例函数有什么区别与联系
反比例关系 反比例函数
区别
联系
如果xy=k(k≠0), 那么x与y两个量成反比例关系, x和y即可以是单项式, 也可以是多项式.
形如
的函数
成反比例关系不一定是反比例函数, 但反比例函数中的两个变量必成反比例关系.
例如, y与x+1成反比例关系, 但y不是x的函数.
典例精析
例1.已知函数.
当m的值是多少时, 函数是反比例函数
解得.
解:由题意得m2-1≠0, 3m2+m-5=-1,
练习3. 当 =___时, 函数是反比例函数.
2
练习4. 若函数是反比例函数,则 的值为___.
2
典例精析
例2.已知y是x的反比例函数, 并且当x=2时, y=6.
(1)求y关于x的函数解析式.
将x=2,y=6代入得k=2×6=12,
∴.
解:设,
(2)当x=4时, 求y的值.
解: 将x=4代入得.
小试锋芒
练习5.已知y是x的反比例函数, 且当x=-2时, y=3.
求y与x的函数解析式;
当x=8时, 求y的值;
当y=2时, 求x的值.
答案: (1) ; (2) ; (3) x=-3.
练习6.已知y与x+1成反比例, 当x=3时, y=4, 那么y=3时, x=___.
典例精析
例3.将油箱加满k L油后, 轿车可行驶的总路程s(km)与平均耗油量a(L/km)之间满足反比例函数关系: (k是常数, k≠0).已知某轿车油箱加满油后, 以平均耗油量为0.1L/km的速度行驶, 可行驶700km.
∴s关于a的函数解析式为.
解: 由题意得k=0.1×700=70,
(1)求s关于a的函数解析式;
(2)当平均耗油量为0.08L/km时, 油箱加满油后该轿车可以行驶多少千米
解: 将a=0.08代入得s==875,
∴该轿车可以行驶875千米.
小试锋芒
练习7.我们中小学生每天都要做眼保健操, 保护视力, 预防近视.已知近视眼镜镜片的度数y(度)与镜片焦距x(cm)(x>0)的调查数据如表:
眼镜片度数y(度) 400 625 800 1000 ... 1250
镜片焦距x(cm) 25 16 12.5 10 ... 8
(1)求y关于x的函数解析式, 它是什么函数
(2)若近视眼镜镜片的度数为500度, 求该镜片的焦距.
答案: (1) ,它是反比例函数;
(2)焦距为20cm.
谢 谢 观 看
第26章 反比例函数
26.1.1
反比例函数
授课:
时间:
问题思考
观察动图, 你能得出怎样的实验现象
实验现象:
①用一根铁钉去扎气球时, 气球立马就炸了;
②用一堆铁钉“齐心协力”去扎气球时, 气球却显得格外的坚硬, 怎么样的都扎不破.
你能解释这是什么原因吗
问题思考
你能解释这是什么原因吗
当按压的力度相同时,
铁钉越多, 气球的受力面积越___, 气球受到的压强越___,气球更不容易爆炸.
反之铁钉越少, 气球的受力面积越___, 气球受到的压强越____, 气球更容易爆炸.
大
小
小
大
气球的受力面积与气球受到的压强成反比例关系.
问题思考
下列问题中, 变量间具有函数关系吗 如果有, 写出函数解析式.
(1) 用20N的力按压气球,铁钉对气球的压强P(Pa) 随着铁钉对气球的受力面积S(m2)的变化而变化.
∵铁钉对气球的受力面积S随着铁钉对气球的压强P变化而变化, 对于S每一个确定的值, P都有唯一的值与之对应,满足函数关系.
∴函数解析式为P= (S > 0).
受力面积S与压强P乘积为定值.
是反比例关系.
问题思考
下列问题中, 变量间具有函数关系吗 如果有, 写出函数解析式.
(2) 昌赣高速铁路全程为416km, 某次列车的平均速度v (km/h)随此次列车的全程运行时间t (h)的变化而变化;
∵列车的平均速度v随着列车的全程运行时间t变化而变化, 对于t每一个确定的值, v都有唯一的值与之对应,满足函数关系.
∴函数解析式为v= (t > 0).
时间t与速度v乘积为定值, 是反比例关系.
问题思考
下列问题中, 变量间具有函数关系吗 如果有, 写出函数解析式.
(3) 已知北京市的总面积为1.64×104 2 , 人均占有面积 (单位: 2/人) 随全市总人口n(单位:人) 的变化而变化.
∵人均占有面积 随着全市总人口n变化而变化, 对于n每一个确定的值, S都有唯一的值与之对应,满足函数关系.
∴函数解析式为S= (n > 0).
总人口n与人均占有面积S乘积为定值, 是反比例关系.
观察思考
P= ,
v= ,
S= .
观察这些函数解析式, 它们有什么共同特征
共同特征: 都是形如的形式.
一般地,形如 (k是常数, )的函数称为反比例函数.
自变量, x≠0
因变量, y≠0
比例系数, k≠0
明察秋毫
练习1. 下列函数是反比例函数的是________.
①; ② ; ③; ④;
⑤; ⑥ ; ⑦; ⑧.
③⑦⑧
反比例函数的三种表达方式(k为常数, k≠0):
, , .
小试锋芒
练习2.用函数解析式表示下列问题中变量间的对应关系:
(1)某住宅小区要种植一块面积为1000m2 的矩形草坪, 草坪的长y(单位:m) 随宽x(单位:m)的变化而变化;
(2)一个游泳池的容积为2000m3, 游泳池注满水所用时间t(单位:h)随注水速度v(单位: m3/h)的变化而变化;
(3)某长方体的体积为1000cm3, 长方体的高h (单位:cm)随底面积S(单位: cm2)的变化而变化.
答案: (1) ; (2); (3).
问题思考
反比例关系和反比例函数有什么区别与联系
反比例关系 反比例函数
区别
联系
如果xy=k(k≠0), 那么x与y两个量成反比例关系, x和y即可以是单项式, 也可以是多项式.
形如
的函数
成反比例关系不一定是反比例函数, 但反比例函数中的两个变量必成反比例关系.
例如, y与x+1成反比例关系, 但y不是x的函数.
典例精析
例1.已知函数.
当m的值是多少时, 函数是反比例函数
解得.
解:由题意得m2-1≠0, 3m2+m-5=-1,
练习3. 当 =___时, 函数是反比例函数.
2
练习4. 若函数是反比例函数,则 的值为___.
2
典例精析
例2.已知y是x的反比例函数, 并且当x=2时, y=6.
(1)求y关于x的函数解析式.
将x=2,y=6代入得k=2×6=12,
∴.
解:设,
(2)当x=4时, 求y的值.
解: 将x=4代入得.
小试锋芒
练习5.已知y是x的反比例函数, 且当x=-2时, y=3.
求y与x的函数解析式;
当x=8时, 求y的值;
当y=2时, 求x的值.
答案: (1) ; (2) ; (3) x=-3.
练习6.已知y与x+1成反比例, 当x=3时, y=4, 那么y=3时, x=___.
典例精析
例3.将油箱加满k L油后, 轿车可行驶的总路程s(km)与平均耗油量a(L/km)之间满足反比例函数关系: (k是常数, k≠0).已知某轿车油箱加满油后, 以平均耗油量为0.1L/km的速度行驶, 可行驶700km.
∴s关于a的函数解析式为.
解: 由题意得k=0.1×700=70,
(1)求s关于a的函数解析式;
(2)当平均耗油量为0.08L/km时, 油箱加满油后该轿车可以行驶多少千米
解: 将a=0.08代入得s==875,
∴该轿车可以行驶875千米.
小试锋芒
练习7.我们中小学生每天都要做眼保健操, 保护视力, 预防近视.已知近视眼镜镜片的度数y(度)与镜片焦距x(cm)(x>0)的调查数据如表:
眼镜片度数y(度) 400 625 800 1000 ... 1250
镜片焦距x(cm) 25 16 12.5 10 ... 8
(1)求y关于x的函数解析式, 它是什么函数
(2)若近视眼镜镜片的度数为500度, 求该镜片的焦距.
答案: (1) ,它是反比例函数;
(2)焦距为20cm.
谢 谢 观 看
