人教版九年级下册27.2.2 相似三角形的性质 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级下册27.2.2 相似三角形的性质 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 670.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 07:14:50 | ||
图片预览

文档简介
(共17张PPT)
第27章 相似
27.2.2
相似三角形的性质
授课:
时间:
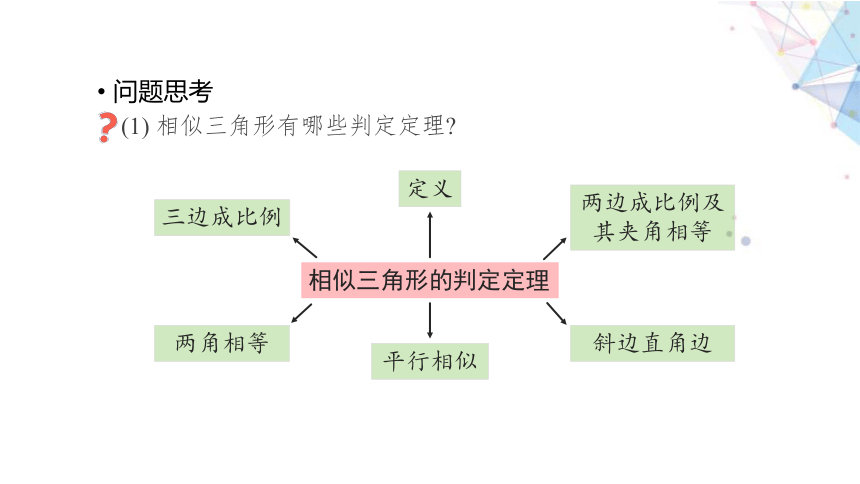
问题思考
(1) 相似三角形有哪些判定定理
相似三角形的判定定理
三边成比例
定义
两边成比例及其夹角相等
两角相等
斜边直角边
平行相似
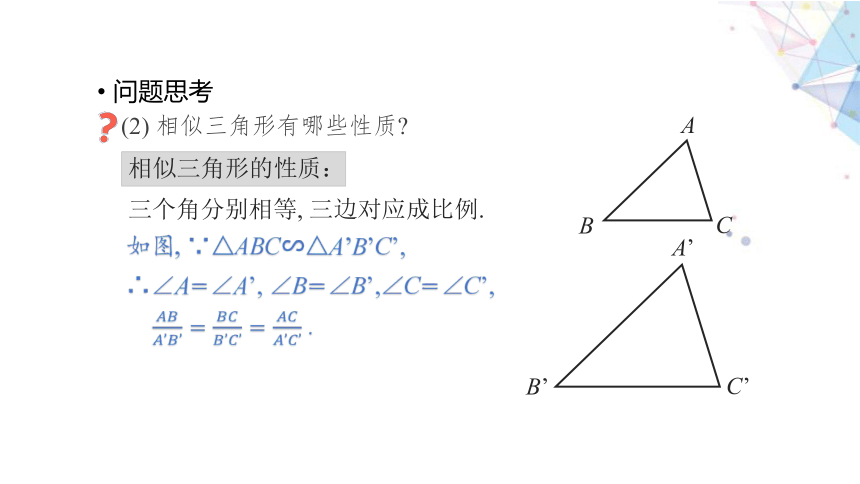
问题思考
(2) 相似三角形有哪些性质
三个角分别相等, 三边对应成比例.
相似三角形的性质:
A
B
C
A’
B’
C’
如图, ∵△ABC∽△A’B’C’,
∴∠A=∠A’, ∠B=∠B’,∠C=∠C’,
.
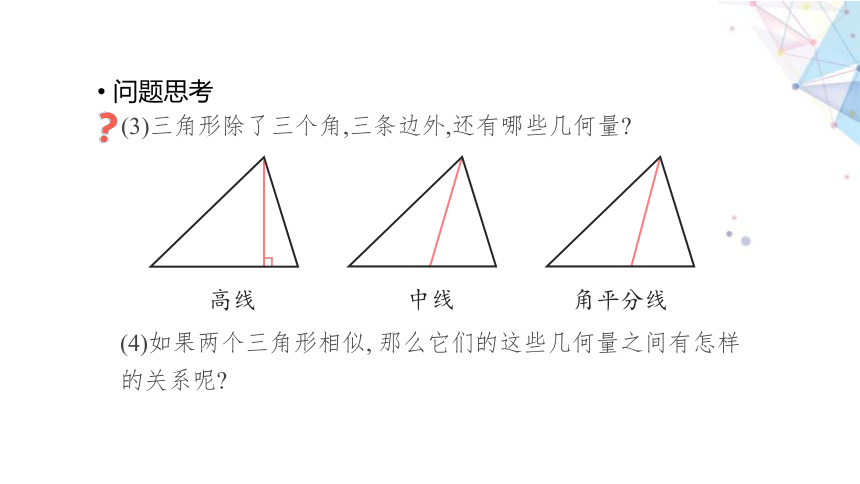
问题思考
(3)三角形除了三个角,三条边外,还有哪些几何量
高线
中线
角平分线
(4)如果两个三角形相似, 那么它们的这些几何量之间有怎样的关系呢
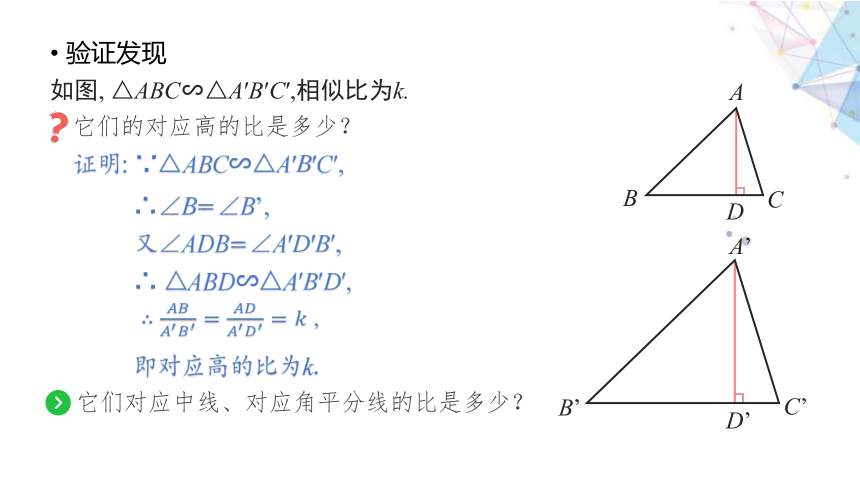
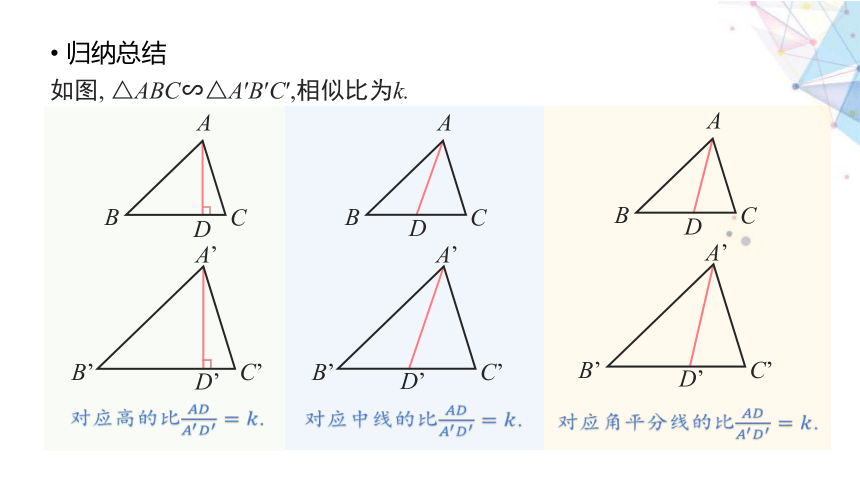
验证发现
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
D
D’
它们的对应高的比是多少?
证明: ∵△ABC∽△A′B′C′,
∴∠B=∠B’,
又∠ADB=∠A′D′B′,
∴ △ABD∽△A′B′D′,
∴ ,
即对应高的比为k.
它们对应中线、对应角平分线的比是多少?
归纳总结
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
D
D’
A
B
C
C’
B’
A’
D
D’
A
B
C
C’
B’
A’
D
D’
对应高的比.
对应中线的比.
对应角平分线的比.
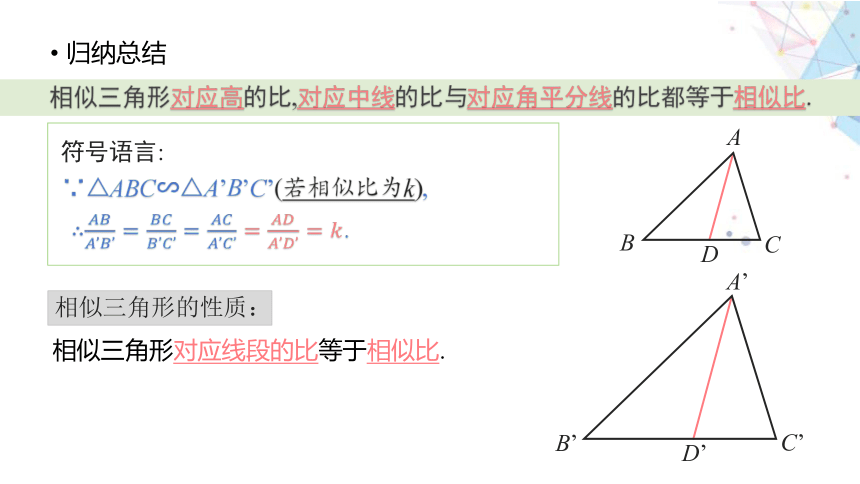
归纳总结
相似三角形对应线段的比等于相似比.
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
A
B
C
C’
B’
A’
D
D’
符号语言:
∵△ABC∽△A’B’C’(若相似比为k),
∴.
相似三角形的性质:
典例精析
例1.如图, △ABC∽△A’B’C’, AD,BE是△ABC的高, A’D’,B’E’是△A’B’C’的高.
探索 与 有怎样的数量关系
证明: ∵△ABC∽△A′B′C′,设相似比为k,
则对应高, ,
∴ .
小试锋芒
练习1.已知△ABC∽△DEF, 且相似比为4:3, 若△ABC中BC边上的中线AM=8, 则△DEF中EF边上的中线DN的长为___.
6
练习2.如果两个三角形相似且相似比为9:16, 那么这两个三角形对应边上的高的比是_____.
9:16
进一步探索
相似三角形的周长比、面积比与相似比怎样的关系
A
B
C
C’
B’
A’
验证发现
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
(1)它们的周长比是多少?
证明: ∵△ABC∽△A′B′C′,
∴ ,
∴
∴ AB=k·A’B’, BC=k·B’C’, AC=k·A’C’,
=k
即周长比为k.
验证发现
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
(2)它们的面积比是多少?
证明: 作△ABC与△A′B′C′的高AD,A’D’,
∴ ,即BC=k·B’C’,AD=k·A’D’,
∴
∵△ABC∽△A′B′C′,
=k2
即面积比为k2.
D
D’
归纳总结
相似三角形的周长比等于相似比, 面积比等于相似比的平方.
A
B
C
C’
B’
A’
符号语言:
∵△ABC∽△A’B’C’(若相似比为k),
∴ .
练习.若△ABC ∽△A’B’C’, AB=2, A’B’=5,
则它们的周长比为____,面积比为____.
典例精析
例2.如图, 在△ABC与△DEF中, AB=2DE,AC=2DF,∠A=∠D.
A
B
C
D
E
F
(1) △ABC与△DEF相似吗
证明: ∵ , ∠A=∠D,
∴△ABC∽△DEF.
(2) 若△ABC的边BC上的高为6, 面积为, 求△DEF的边EF上的高和面积.
解: 由(1)得△ABC与△DEF的相似比为2,
∴对应高的比为2, 则边EF上的高为 =3,
面积比为4, 则△DEF的面积为.
小试锋芒
练习3. 已知△ABC∽△DEF, 且对应角平分线之比为4:9, 则△ABC与△DEF的周长之比为_____,面积之比为_______.
4:9
练习4.已知两个相似三角形的面积比为4:9, 则这两个相似三角形的对应边之比是____.
2:3
16:81
练习5.若将一个三角形边长扩大为原来的5倍, 那么周长扩大为原来的____倍; 面积扩大为原来的_____倍.
25
5
小试锋芒
练习6.如图, 在△ABC中, EF//BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( ).
A.16 B.18
C.20 D.24
B
谢 谢 观 看
第27章 相似
27.2.2
相似三角形的性质
授课:
时间:
问题思考
(1) 相似三角形有哪些判定定理
相似三角形的判定定理
三边成比例
定义
两边成比例及其夹角相等
两角相等
斜边直角边
平行相似
问题思考
(2) 相似三角形有哪些性质
三个角分别相等, 三边对应成比例.
相似三角形的性质:
A
B
C
A’
B’
C’
如图, ∵△ABC∽△A’B’C’,
∴∠A=∠A’, ∠B=∠B’,∠C=∠C’,
.
问题思考
(3)三角形除了三个角,三条边外,还有哪些几何量
高线
中线
角平分线
(4)如果两个三角形相似, 那么它们的这些几何量之间有怎样的关系呢
验证发现
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
D
D’
它们的对应高的比是多少?
证明: ∵△ABC∽△A′B′C′,
∴∠B=∠B’,
又∠ADB=∠A′D′B′,
∴ △ABD∽△A′B′D′,
∴ ,
即对应高的比为k.
它们对应中线、对应角平分线的比是多少?
归纳总结
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
D
D’
A
B
C
C’
B’
A’
D
D’
A
B
C
C’
B’
A’
D
D’
对应高的比.
对应中线的比.
对应角平分线的比.
归纳总结
相似三角形对应线段的比等于相似比.
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
A
B
C
C’
B’
A’
D
D’
符号语言:
∵△ABC∽△A’B’C’(若相似比为k),
∴.
相似三角形的性质:
典例精析
例1.如图, △ABC∽△A’B’C’, AD,BE是△ABC的高, A’D’,B’E’是△A’B’C’的高.
探索 与 有怎样的数量关系
证明: ∵△ABC∽△A′B′C′,设相似比为k,
则对应高, ,
∴ .
小试锋芒
练习1.已知△ABC∽△DEF, 且相似比为4:3, 若△ABC中BC边上的中线AM=8, 则△DEF中EF边上的中线DN的长为___.
6
练习2.如果两个三角形相似且相似比为9:16, 那么这两个三角形对应边上的高的比是_____.
9:16
进一步探索
相似三角形的周长比、面积比与相似比怎样的关系
A
B
C
C’
B’
A’
验证发现
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
(1)它们的周长比是多少?
证明: ∵△ABC∽△A′B′C′,
∴ ,
∴
∴ AB=k·A’B’, BC=k·B’C’, AC=k·A’C’,
=k
即周长比为k.
验证发现
如图, △ABC∽△A′B′C′,相似比为k.
A
B
C
C’
B’
A’
(2)它们的面积比是多少?
证明: 作△ABC与△A′B′C′的高AD,A’D’,
∴ ,即BC=k·B’C’,AD=k·A’D’,
∴
∵△ABC∽△A′B′C′,
=k2
即面积比为k2.
D
D’
归纳总结
相似三角形的周长比等于相似比, 面积比等于相似比的平方.
A
B
C
C’
B’
A’
符号语言:
∵△ABC∽△A’B’C’(若相似比为k),
∴ .
练习.若△ABC ∽△A’B’C’, AB=2, A’B’=5,
则它们的周长比为____,面积比为____.
典例精析
例2.如图, 在△ABC与△DEF中, AB=2DE,AC=2DF,∠A=∠D.
A
B
C
D
E
F
(1) △ABC与△DEF相似吗
证明: ∵ , ∠A=∠D,
∴△ABC∽△DEF.
(2) 若△ABC的边BC上的高为6, 面积为, 求△DEF的边EF上的高和面积.
解: 由(1)得△ABC与△DEF的相似比为2,
∴对应高的比为2, 则边EF上的高为 =3,
面积比为4, 则△DEF的面积为.
小试锋芒
练习3. 已知△ABC∽△DEF, 且对应角平分线之比为4:9, 则△ABC与△DEF的周长之比为_____,面积之比为_______.
4:9
练习4.已知两个相似三角形的面积比为4:9, 则这两个相似三角形的对应边之比是____.
2:3
16:81
练习5.若将一个三角形边长扩大为原来的5倍, 那么周长扩大为原来的____倍; 面积扩大为原来的_____倍.
25
5
小试锋芒
练习6.如图, 在△ABC中, EF//BC,AB=3AE,若S四边形BCFE=16,则S△ABC=( ).
A.16 B.18
C.20 D.24
B
谢 谢 观 看
