2025高考数学【名校真题】经典必刷-专项训练(12套)(PDF版,含解析)
文档属性
| 名称 | 2025高考数学【名校真题】经典必刷-专项训练(12套)(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 17:48:38 | ||
图片预览




文档简介
2025 届新高考数学名校真题经典必刷卷
名校经典真题汇编 (一) 2
名校经典真题汇编 二 8
名校经典真题汇编 (三) 15
名校经典真题汇编 (四) 22
名校经典真题汇编 (五) 28
名校经典真题汇编 (六) 36
名校经典真题汇编 (七) 42
名校经典真题汇编 (八) 48
名校经典真题汇编 (九) 54
名校经典真题汇编 (十) 60
名校经典真题汇编 (十一) 67
名校经典真题汇编 (十二) 74
1
宝剑锋从磨砺出
名校真题
名校经典真题汇编 (一)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中,只有一
项是符合题目要求的.)
1 已知集合 M={x ∣ 2x+ 1< 3},N={x ∣ x< a} ,若 M∩N=N ,则实数 a的取值范围为
( )
A. [1, +∞) B. [2, +∞) C. (-∞,1] D. -∞,1
2 若实数 x,y满足 x+ i 3+yi = 2+ 4i ,则 xy= ( )
A. - 1 B. 1 C. 3 D. - 3
3 设点 A,B,C 不共线,则“ AB 与 AC 的夹角是锐角”是“ AB+AC > BC ”的 ( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
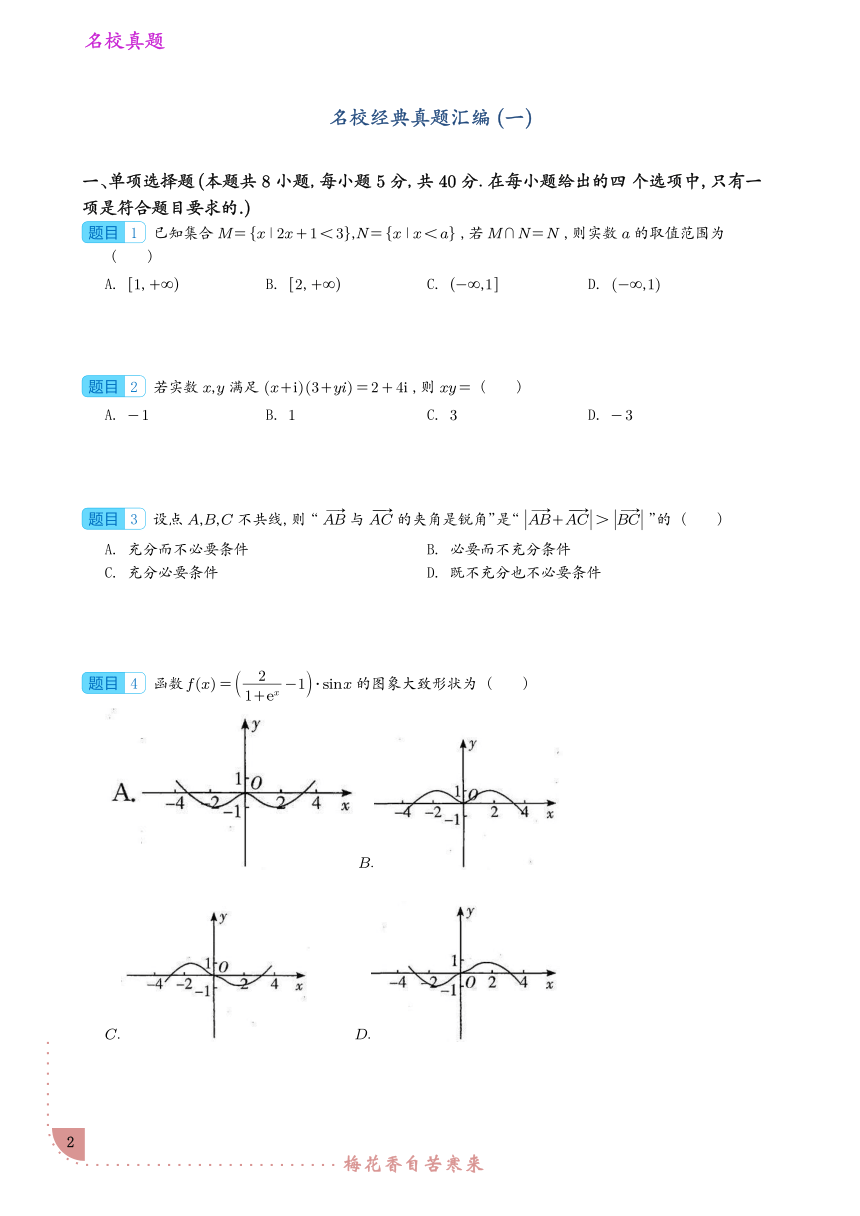
4 函数 f x = 2 -11+ex sinx的图象大致形状为 ( )
B.
C. D.
2
梅花香自苦寒来
名校真题
5 在圆的内接四边形 ABCD中, AD= 2,CD= 4,BD是圆的直径, 则 AC BD等于 ( )
A. 12 B. - 12 C. 20 D. - 20
6 在三棱锥 P-ABC 中, PA⊥底面 ABC,PA= 2 ,底面 ABC 是边长为 2 3 的正三角形, M 为
AC 的中点,球 O是三棱锥 P-ABM 的外接球, 若 D是球 O上一点,则三棱锥 D-PAC 的体积的最
大值是 ( )
2 2 3 7 3 8 3A. B. C. D.
3 3
7 古希腊数学家欧几里得在《几何原本》中描述了圆锥曲线的共性, 并给出了圆锥曲线的统一定义,
只可惜对这一定义欧几里得没有给出证明. 经过了 500年, 到了 3世纪, 希腊数学家帕普斯在他的著作
《数学汇篇》中, 完善了欧几里得关于圆锥曲线的统一定义, 并对这一定义进行了证明. 他指出,到定点的
距离与到定直线的距离的比是常数 e的点的轨迹叫做圆锥曲线;当 0< e< 1时,轨迹为椭圆;当 e= 1
时,轨迹为抛物线;当 e> 1时,轨迹为双曲线. 现有方程 m x2+y2+2y+1 = x-2y+3 2 表示的曲线
是双曲线,则 m的取值范围为 ( )
A. (0,1) B. 1,+∞ C. (0,5) D. 5,+∞
8 函数 f x = sin ωx+φ ω>0, φ ≤ π ,已知 - π ,0 为 f x 图象的一个对称中心,直线 x=2 6
13π 为 f x 图象的一条对称轴,且 f x 在 13π , 19π 12 上单调递减. 记满足条件的所有 ω的值的和为12 12
S ,则 S的值为 ( )
12 8 16 18
A. B. C. D.
5 5 5 5
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 已知 a,b,c为正实数,且 ab+ ac= 2 ,则 1 + 1 + 8 的取值不可能是 ( )
a b+c a+b+c
A. 1 B. 2 C. 3 D. 4
3
宝剑锋从磨砺出
名校真题
10 已知 1+2x n = a0+ a1x+ a x22 + +anxn ,下列结论正确的是 ( )
A. a + a + a + +a = 3n0 1 2 n
B. 当 n= 5,x= 3 时,设 1+2x n = a+ b 3 a,b∈N * ,则 a= b
C. 当 n= 12时, a0,a1,a2, ,an 中最大的是 a7
D. 当 n= a12时, 1 - a2 + a3 - a4 + + a11 - a12 = 1
2 22 23 24 211 212
11 已知定义在 R上的函数 f x 满足:当 x≥ 0时, f 1+x = 2f 1-x , 且当 x> 0时, f 1+x
+ f 1-x < 0 ,则下列说法正确的是 ( )
A. f 1 = 0
B. f x 在 (-∞,1]上单调递减
C. 若 x1< x2,f x1 < f x2 ,则 x1+ x2< 2
f x
D. 若 x1,x2 是 g x = f x - cosπx
2
在区间 (0,2)内的两个零点,且 x1< x2 ,则 1< < 2
f x1
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
2 y2
12 已知 F1,F2 是双曲线 x - = 1 a>0,b>0 的左、右焦点,若点 F2 关于双曲线渐近线的对称
a2 b2
点 A满足 ∠F1AO=∠AOF1 O为坐标原点 , 则双曲线的渐近线方程为 .
13 已知四面体 ABCD的各条棱长都为 2,其顶点都在球 O的表面上,点 E 满足 BE= 1 BD ,过
3
点 E 作平面 α ,则平面 α截球 O所得截面面积的取值范围是 .
14 已知 m,n为实数, f x = ex-mx+n- 1 ,若 f x ≥ 0对 x∈R恒成立, 则 n 的最小值是
m
.
4
梅花香自苦寒来
名校真题
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演 算步骤.)
15 (本小题满分 13分)
S
已知正项数列 an 的前 n项和为 S
n+1 n+2
n ,满足 = ,a1= 1 .Sn n
(1)求数列 an 的通项公式;
( ) , = 2+a2 数列 bn 为等比数列 数列 c nn 满足 cn ,若 b2= 2 ,an an+1 bn+1
b b b b b = 2101 2 3 4 5 ,求证: c1+ c2+ +cn< 1 .
16 (本小题满分 15分)
在直角梯形 AA1B1B 中, A1B1 AB , AA1⊥ AB,AB=AA1= 2A1B1= 6 ,直角梯形 AA1B1B 绕直角边
AA1 旋转一周得到如右图的圆台 A1A ,已知点 P , Q 分别在线段 CC1 , BC 上,二面角 B1-AA1-C1
的大小为 θ .
(1)若 θ= 120°,CP= 2 CC1,AQ⊥AB ,证明: PQ 平面 AA1B3 1B ;
(2)若 θ= 90° ,点 Q、N 分别为 BC 、AC 的中点, NP⊥CC1 ,求二面角 Q- AP-C 的余弦值.
5
宝剑锋从磨砺出
名校真题
17 (本小题满分 15分)
已知 F 是抛物线 C :x2= 2py p>0 的焦点,以 F 为圆心, 2p 为半径的圆 F 与抛物线 C 交于 A,B 两
点,且 AB = 4 3 .
(1)求抛物线 C 和圆 F 的方程;
(2)若点 P 为圆 F 优弧 AB 上任意一点,过点 P 作抛物线 C 的两条切线 PM ,PN ,切点分别为 M ,N ,
请问 MF NF 是否为定值 若是, 求出该定值;若不是, 请说明理由.
18 (本小题满分 17分)
某学校为了弘扬中华传统文化,组织开展中华传统文化活动周,活动周期间举办中华传统文化知识竞赛
活动, 以班级为单位参加比赛, 每班通过中华传统文化知识竞答活动, 择优选拔 5 人代表班级参加年级
比赛. 年级比赛分为预赛与决赛二阶段进行, 预赛阶段的赛制为:将两组中华传统文化的问答题放在甲、
乙两个纸箱中, 甲箱有 5 个选择题和 3 个填空题,乙箱中有 4 个选择题和 3 个填空题,比赛中要求每个
班级代表队在甲或乙两个纸箱中随机抽取两题作答. 每个班级代表队先抽取一题作答, 答完后试题不放
回纸箱中, 再抽取第二题作答, 两题答题结束后, 再将这两个试题放回原纸箱中.
(1)若 1 班代表队从甲箱中抽取了 2 个试题,答题结束后错将题目放入了乙箱中, 接着 2 班代表队答题,
2 班代表队抽取第一题时, 从乙箱中抽取试题. 已知 2 班代表队从乙箱中取出的是选择题, 求 1 班代表
队从甲箱中取出的是 2个选择题的概率;
(2)经过预赛,成绩最好的 6 班代表队和 18 班代表队进入决赛,决赛采用成语接龙的形式进行, 采用五
局三胜制, 即两班代表队中先胜三局的代表队赢得这场比赛, 比赛结束. 已知第一局比赛 6 班代表队获
胜的概率为 3 ,18班代表队胜的概率为 2 ,且每一局的胜者在接下来一局获胜的概率为 2 ,每局必分
5 5 5
胜负. 记比赛结束时比赛局数为随机变量 X ,求随机变量 X 的数学期望 E X .
6
梅花香自苦寒来
名校真题
19 (本小题满分 17分)
已知函数 f x = x+n lnx .
(1)若 n= 1 ,求函数 g x = f x - k x-1 k>2 的零点个数,并说明理由;
-3
(2)当 n= 0时,若方程 f x = b有两个实根 x1,x2 ,且 x1< x2 ,求证:be+ 1< x2- x < e +2+3b1 .2
7
宝剑锋从磨砺出
名校真题
名校经典真题汇编 二
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 若以集合 A的四个元素 a,b,c,d为边长构成一个四边形,则这个四边形可能是 ( )
A. 梯形 B. 平行四边形 C. 菱形 D. 矩形
2 在复平面内,复数 z所对应的点的坐标为 (1, - 1),则 z z= ( )
A. 2 B. - 2i C. 2 D. 2i
3 1947年, 生物学家 Max Kleiber发表了一篇题为《body size and metabolic rate》的论文, 在论
文中提出了一个克莱伯定律:对于哺乳动物,其基础代谢率与体重的 3
3
次幂成正比,即 F= c M 40 ,其4
中 F 为基础代谢率, M 为体重. 若某哺乳动物经过一段时间生长,其体重为原来的 10倍,则基础代谢率
为原来的 ( )
1 1 3
A. 10 4 倍 B. 10 2 倍 C. 10 4 倍 D. 10倍
8
梅花香自苦寒来
名校真题
4 已知函数 f x = x + sin2x ,设 x1,x2∈R ,则 f x1 > f x2 成立的一个必要不充分条件是
( )
A. x1> x2 B. x2> x1 C. x1+ x2> 0 D. x1 > x2
5 如图,圆 M : x-2 2 + y2= 1 ,点 P -1,t 为直线 l:x=-1上一动点,过点 P引圆 M 的两条切
线,切点分别为 A,B . 若两条切线 PA,PB 与 y轴分别交于 S、T 两点,则 ST 的最小值为 ( )
1 2
A. B. C. 1 D. 2
2 2
6 某旅游景区有如图所示 A至 H 共 8个停车位,现有 2辆不同的白色车和 2辆不同的黑色车, 要
求相同颜色的车不停在同一行也不停在同一列, 则不同的停车方法总数为 ( )
A B C D
E F G H
A. 288 B. 336 C. 576 D. 1680
7 在平面直角坐标系 xOy中,已知过抛物线 y2= 4x焦点 F 的直线与抛物线相交于 A,B 两点,以
AF,BF 为直径的圆分别与 x轴交于异于 F 的 P,Q两点,若 PF = 2 FQ ,则线段 AB 的长为
( )
5 7 9 13
A. B. C. D.
2 2 2 2
9
宝剑锋从磨砺出
名校真题
8 若正实数 a,b满足 a> b ,且 lna lnb> 0 ,则下列不等式一定成立的是 ( )
log b< 0 a- 1 > b- 1A. a B. C. 2ab+1< 2a+b D. ab-1< ba-1b a
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 已知随机变量 X 服从正态分布 N 0,1 ,定义函数 f x 为 X 取值不超过 x的概率,即 f x =
P X≤x . 若 x> 0 ,则下列说法正确的有 ( )
A. f -x = 1- f x B. f 2x = 2f x
C. f x 在 0,+∞ 上是增函数 D. P X ≤x = 2f x - 1
10 在棱长为 a的正方体 ABCD-A1B1C1D1 中, B1D与平面 ACD1 相交于点 E,P为 △ACD1 内一
点,且 S 1△PB D= S△ACD ,设直线 PD与 ( )1 3 1
A1C1 所成的角为 θ ,则下列结论正确的是
A. B1D⊥PE B. 点 P的轨迹是圆
C. 点 P的轨迹是椭圆 D. θ的取值范围是 π , π 3 2
11 已知数列 an 满足 a ean+1n = ean- 1 ,且 a1= 1, Sn 是数列 an 的前 n项和,则下列结论正确
的是 ( )
A. an> 0 B. an+1> an
C. a2021+ a2023> 2a2022 D. S2023> 2
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 设平面向量 a,b的夹角为 60° ,且 a = b = 2 ,则 a在 b上的投影向量是 .
10
梅花香自苦寒来
名校真题
13 如图,在四棱锥 P-ABCD中,底面 ABCD为菱形, PD⊥底面 ABCD,O为对角线 AC 与
BD的交点,若 PD= 3,∠APD=∠BAD = π ,则三棱锥 P-AOD的外接球的体积为 .
3
14 若直线 l:y= kx+ b为曲线 f x = ex 与曲线 g x = e2 lnx的公切线 (其中 e为自然对数的底
数, e≈ 2.71828 ),则实数 b的值是
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演 算步骤.)
15 (本小题满分 13分)
在 △ABC 中,内角 A,B,C 的对边分别为 a,b,c ,已知 (1+ sinB+ cosB) cosB -sinB = 7 cosB .2 2 6 2
(1)求 cosB ;
(2)若 a= 3,c= 2,D为边 AC 上一点,且 BD=AC ,求 AD 的值.
DC
11
宝剑锋从磨砺出
名校真题
16 (本小题满分 15分)
如图,在四棱锥 P-ABCD中,平面 PAD⊥平面 ABCD,PA=AD= 2 ,
BD= 4,AB= 2 3 ,BD是 ∠ADC 的平分线,且 BD⊥BC .
(1)若点 E 为棱 PC 的中点,证明: BE 平面 PAD;
(2)已知二面角 P-AB-D的大小为 60° ,求平面 PBD和平面 PCD的夹角的余弦值.
17 (本小题满分 15分)
为了检测某种抗病毒疫苗的免疫效果, 需要进行动物与人体试验. 研究人员将疫苗注射到 200 只小白鼠
体内,一段时间后测量小白鼠的某项指标值,按 [0,20),[20,40),[40,60),[60,80) , 80,100 分组,绘制频
率分布直方图如图所示. 试验发现小白鼠体内产生抗体的共有 160 只, 其中该项指标值不小于 60 的有
110只.
假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的 2× 2列联表,并根据列联表及 α= 0.05的独立性检验, 判断能否认为注射疫苗后小白鼠
12
梅花香自苦寒来
名校真题
产生抗体与指标值不小于 60有关;
单位:只
抗体 指标值 合计
小于 60 不小于 60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的 40 只小白鼠进行第二次
注射疫苗,结果又有 20只小白鼠产生抗体.
( i )用频率估计概率,求一只小白鼠注射 2次疫苗后产生抗体的概率 p;
(ii) 以 (i)中确定的概率 p 作为人体注射 2 次疫苗后产生抗体的概率,进行人体接种试验,记 n 个人注
射 2 次疫苗后产生抗体的数量为随机变量 X . 试验后统计数据显示,当 X= 99 时, P X 取最大值,求
参加人体接种试验的人数 n及 E X .
n ad-bc 2
参考公式: χ2= (其中 n= a+ b+ c+ d为样本容量).
a+b c+d a+c b+d
α 0.50 0.40 0.25 0.15 0.100 0.050 0.025
xα 0.455 0.708 1.323 2.072 2.706 3. 841 5.024
18 (本小题满分 17分)
已知 A -2 2,0 ,B 2 2,0 ,直线 PA,PB 的斜率之积为 - 3 ,记动点 P的轨迹为曲线 C .
4
(1)求 C 的方程;
(2)直线 l 与曲线 C 交于 M ,N 两点, O 为坐标原点,若直线 OM ,ON 的斜率之积为 - 3 ,证明:
4
△MON 的面积为定值.
13
宝剑锋从磨砺出
名校真题
19 (本小题满分 17分)
已知函数 f x = 2x- sinx- alnx .
(1)当 a= 0时, x∈ 0, π ,f x ≤mx ,求实数 m的取值范围;2
(2)若 x1,x2∈ 0,+∞ ,x1≠ x2 ,使得 f x1 = f x2 ,求证:x1x2< a2.
14
梅花香自苦寒来
名校真题
名校经典真题汇编 (三)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中,只有一
项是符合题目要求的. )
1 已知集合 A= x∣x2-3x<0 ,B={1,2,3,4} ,则 RA ∩B= ( )
A. {3,4} B. {1,2} C. {2,3,4} D. {1,2,3}
2 一学习小组 10名学生的某次数学测试成绩的名次由小到大分别是 2 , 4,5,x,11,14,15,39,41,50 ,
已知该小组数学测试成绩名次的 40%分位数是 9.5,则 x的值是 ( )
A. 6 B. 7 C. 8 D. 9
3 已知模为 2的复数 z对应的向量为 OZ ( O为坐标原点),它对应的点位于第二象限, OZ 与实轴
正向的夹角为 150° ,则复数 z为 ( )
A. 1+ 3 i B. 2 C. - 1- 3 i D. - 3+ i
4 如图,一个装有某种液体的圆柱形容器固定在墙面和地面的角落内,容器与地面所成的角为 30° ,
液面呈椭圆形,椭圆长轴上的顶点 M ,N 到容器底部的距离分别是 10和 16 , 则容器内液体的体积是
( )
A. 36π B. 39π C. 42π D. 45π
15
宝剑锋从磨砺出
名校真题
5 如图甲所示, 古代中国的太极八卦图是以同圆内的圆心为界, 画出相等的两个阴阳鱼, 阳鱼的头
部有眼, 阴鱼的头部有个阳殿, 表示万物都在相互转化, 互相渗透, 阴中有阳, 阳中有阴, 阴阳相合, 相生
相克, 蕴含现代哲学中的矛盾对立统一规律. 其平面图形记为图乙中的正八边形 ABC-DEFGH ,其中
OA= 2 ,则以下结论错误的是 ( )
甲
乙
A. 2OB+OE+OG= 0 B. OA OD=-2 2
C. AG+EH = 4 D. AO在 OH 方向上的投影向量为 - 2 OH2
6 已知函数 f x = cos ωx+φ ω>0,0<φ<π 的图象的一条对称轴与其相邻的一个对称中心的
距离为 π ,将 f x π 的图象向右平移 个单位长度得到函数 g x 的图象. 若函数 g x 的图象在区间
4 6
π ,
3π
上是增函数,则 φ的取值范围为 ( )2 4
π , π π , 5π π , 2πA. B. C. π 3π 6 2 D. ,3 6 3 3 4 4
16
梅花香自苦寒来
名校真题
7 设 a= cos π - π ,b= π - sin π ,c= tan π - π ,则 ( )
11 11 11 11 11 11
A. b< c< a B. c< b< a C. c< a< b D. a< b< c
8 截角八面体是由正四面体经过适当的截角, 即截去正四面体的四个顶点处的小棱锥所得的八面
体. 如图所示,有一个所有棱长均为 a的截角八面体石材, 现将此石材切削、打磨、加工成球, 则加工后球
的最大表面积为 ( )
πa2 3A. B. πa2 5C. πa2 8D. πa2
2 3 3
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 假设某市场供应的智能手机中,市场占有率和优质率的信息如表:在该市场中任意买一部手机,
用 A1,A2,A3 分别表示买到的智能手机为甲品牌、乙品牌,其他品牌, B 表示可买到的优质品,则 ( )
品牌 甲 乙 其他
市场占有率 50% 30% 20%
优质率 80% 90% 70%
A. P A1 = 0.50 B. P B∣A2 = 0.90 C. P BA3 = 0.70 D. P B = 0.81
10 已知函数 f x = 2 sinx+cosx - sin2x ,则 ( )
π
A. 函数 y= f x 的最小正周期为 2π B. x=- 为函数 y= f x 的一条对称轴
4
C. 函数 f x 的最小值为 1 D. 函数 f x 的最大值为 2
17
宝剑锋从磨砺出
名校真题
11 已知 F 是抛物线 C:y2= 4x的焦点, A,B 是抛物线 C 上的两点, O为坐标原点, 则 ( )
A. 曲线 C 的准线方程为 x=-2
B. 若 AF = 4 ,则 △AOF 的面积为 3
C. 若 OA⊥OB ,则 OA OB ≥ 32
D. 若 ∠AFB= 60°,AB 的中点 M 在 C 的准线上的投影为 N ,则 MN ≤ AB
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 已知: A -2,0 ,B 2,0 ,C 0,2 ,E -1,0 ,F 1,0 ,一束光线从 F 点出发射到 BC 上的 D点经
BC 反射后,再经 AC 反射,落到线段 AE 上 (不含端点). 则 FD斜率的取值范围是 .
13 已知抛物线 C:x2=-8y的焦点为 F ,过 F 的直线 l与抛物线 C 相交于 A,B 两点,分别过 A,B
两点作 C 的切线 l1,l2 ,且 l1,l2 相交于点 P ,则 △PAB 面积的最小值为 .
14 已知函数 f x = ex- aln ax-a + a a>0 ,若关于 x的不等式 f x > 0恒成立,则实数 a的
取值范围为 .
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤.)
15 (本小题满分 13分)
如图,在直三棱柱 ABC-A1B1C1 中, AB=BB1= 2,BC⊥BA1 .
(1)求证: BC⊥AB ;
(2)若 E 为 A1B 的中点,三棱锥 A-CEA1 的体积为 1 ,线段 CE 上是否存在点 P ,使得二面角 P-3
AB-E 的大小为 30° 若存在,求 EP 的值,若不存在,请说明理由.
EC
18
梅花香自苦寒来
名校真题
16 (本小题满分 15分)
已知数列 an 各项都不为 0,a1= 2,a2= 4, an 的前 n项和为 Sn ,且满足 anan+1= 4Sn .
(1)求 an 的通项公式;
b +2n+1(2)若 bn= a1C1n+ a2C2 3 n-1 n nn+ a3Cn+ +an-1Cn + anCn ,求数列 的前 n项和 Tb b n .n n+1
19
宝剑锋从磨砺出
名校真题
17 (本小题满分 15分)
2022 年 12 月 15 至 16 日,中央经济工作会议在北京举行. 关于房地产主要有三点新提法,其中“住房改
善”位列扩大消费三大抓手的第一位. 某房地产开发公司旗下位于生态公园的楼盘贯彻中央经济工作会
议精神,推出了为期 10 天的促进住房改善的惠民优惠售房活动,该楼盘售楼部统计了惠民优惠售房活
动期间到访客户的情况, 统计数据如下表: (注:活动开始的第 i天记为 xi ,第 i天到访的人次记为 yi,i=
1,2 ,3, )
xi (单 1 2 3 4 5 6 7
位:天)
yi (单位: 12 22 42 68 132 202 392
人次)
(1)根据统计数据,通过建模分析得到适合函数模型为 y= c dx(c,d 均为大于零的常数). 请根据统计数
据及上表中的数据, 求活动到访人次 y关于活动开展的天次 x的回归方程,并预测活动推出第 8天售楼
部来访的人次;
(2)该楼盘营销策划部从有意向购房的客户中,随机通过电话进行回访,统计有效回访发现,客户购房意
向的决定因素主要有三类: A类是楼盘的品质与周边的生态环境, B 类是楼盘的品质与房子的设计布局,
C 类是楼盘的品质与周边的生活与教育配套设施. 统计结果如下表:
类别 A类 B类 C类
频率 0.4 0.2 0.4
从被回访的客户中再随机抽取 3 人聘为楼盘的代言人, 视频率为概率,记随机变量 X 为被抽取的 3 人
中 A类和 C 类的人数之和,求随机变量 X 的分布列和数学期望.
7 7
参考数据:其中 vi= lgy ,v
1
i = vi= 1.84, x v = 58.55,100.847 i i ≈i=1 i=1
20
梅花香自苦寒来
名校真题
18 (本小题满分 17分)
参考公式:对于一组数据 u1,v1 , u2,v2 , , un,vn ,其回归直线 v= α+ βu的斜率和截距的最小二乘
估计公式分别为:
n n
ui-v vi-v uivi-nuv
β= i=1 = i=1 n n
,α= v- βu.
2 u -u u2i i-nu 2
i=1 i=1
: x
2
+ y
2
已知椭圆 C = 1 a>b>0 过点 M
a2 b2 1,
6 ,点 A为其左顶点,且 AM 的斜率为 6 .2 6
(1)求 C 的方程;
(2) P , Q为椭圆 C 上两个动点,且直线 AP 与 AQ的斜率之积为 - 1 , MD⊥PQ,D 为垂足. 求 AD
6
的最大值.
19 (本小题满分 17分)
已知函数 f x = aex- ln x+a - 1 .
(1)若 f x 的极小值为 0,求实数 a的值;
(2)当 a> 0时,证明: f x 存在唯一极值点 x0 ,且 f x0 + 2 x0 ≥ 0 .
21
宝剑锋从磨砺出
名校真题
名校经典真题汇编 (四)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知 a∈R ,若复数 z= a2-1 + a+1 i为纯虚数,则复数 2+i - 在复平面内对应的点所在的a i
象限为 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2 设 x∈R ,向量 a= 1,2 ,b= x,1 ,c= 4,x ,则“ a⊥ b”是“ b c”的 ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
3 如图所示, A,B 是非空集合,定义集合 A#B 为阴影部分表示的集合. 若 x∈R,A=
x∣0
若 α∈ - π ,- π ,且 cos2α+ cos 3π4 +2α =- 1 ,则 tanα= ( )2 4 2 2
A. - 3 B. - 2 C. - 3 D. - 2 3
5 甲、乙两名司机的加油习惯有所不同,甲每次加油都说“师傅,给我加 300元的油”, 而乙则说“师
傅帮我把油箱加满”, 如果甲、乙各加同一种汽油两次,两人第一次与第二次加油的油价分别相同,但第
一次与第二次加油的油价不同, 乙每次加满油箱, 需加入的油量都相同, 就加油两次来说 ( )
A. 甲更合算 B. 乙更合算 C. 甲乙同样合算 D. 无法判断谁更合算
22
梅花香自苦寒来
名校真题
6 《红海行动》是一部现代海军题材影片, 该片讲述了中国海军“蛟龙突击
队”奉命执行撤侨任务的故事. 撤侨过程中, 海军舰长要求队员们依次完成六项任务,并对任务的顺序提
出了如下要求:重点任务 A必须排在前三位,且任务 E,F 必须排在一起,则这六项任务的不同安排方案
共有 ( )
A. 240种 B. 188种 C. 156种 D. 120种
7 在四面体 PABC 中, PA⊥AB,PA⊥AC,∠BAC= 120°,AB=AC= AP= 2 ,则该四面体的外
接球的表面积为 ( )
A. 12π B. 16π C. 18π D. 20π
8 设 f x 是定义在 R上的函数,若 f x + x2 是奇函数, f x - x是偶函数,函数 g x =
f x ,x∈ 0,1 , 若对任意的 x∈ 0,m , g x ≤ 3恒成立,则实数 m的最大值为 ( )2g x-1 ,x∈ 1,+∞ ,
13 17 9 14
A. B. C. D.
3 4 2 3
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
2 y2
9 已知椭圆 C: x + = 1,F1,F2 是椭圆 C 的两个焦点, M ,N 是椭圆 C 上两点,且 M ,N 分别在25 16
x轴两侧,则 ( )
A. 若直线 MN 经过原点,则四边形 MF1NF2 为矩形
B. 四边形 MF1NF2 的周长为 20
C. △MF1F2 的面积的最大值为 12
D. 若直线 MN 经过 F2 ,则 F1 到直线 MN 的最大距离为 8
10 已知函数 f x = ex-1+ ax2+ 1的图象在 x= 1处的切线与直线 3x- y +1= 0平行,若存在 x0
> 0 ,使得不等式 f x0 ≤ kx0 成立,则实数 k的值可以是 ( )
A. 1 B. 2 C. 3 D. 4
23
宝剑锋从磨砺出
名校真题
11 如图,正方体 ABCD-A1B1C1D1 中,顶点 A在平面 α内,其余顶点在 α的同侧,顶点 B,C,A1
到 α的距离分别为 1,2,3,则 ( )
A. BD 平面 α B. 平面 A1AC⊥平面 α
C. 直线 AB1 与 α所成角比直线 AA1 与 α所成角大 D. 正方体的棱长为 11
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 x-2y+z 8 的展开式中 x3y3z2 的系数是 (用数字作答).
a
13 已知数列 an 满足: an+ a * 9n+2= 2an+1 对 n∈N 恒成立,且 <-1 ,其前 n项和 Sn 有最大a8
值,则使得 Sn> 0的最大的 n的值是 .
2 2
14 F1,
y
F2 为双曲线 C: x - = 1 a>b>0 的左、右焦点,过点 F1 且斜率为 1的直线与两条渐近
a2 b2
AF1
线分别交于 A,B 两点,若 = 1 ,P 4, 3 为双曲线 C 上一点, △PF1F2 的内切圆圆心为 I ,过 F2
BF1 3
作 F2T⊥PI ,垂足为 T,O为坐标原点,则 OT = .
24
梅花香自苦寒来
名校真题
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演 算步骤.)
15 (本小题满分 13分)
在① b-c sin A+C +sin A+B = b-a sin B+C ; ② (b - 2a). cos A+B + c cos A+C =
0 ,这两个条件中任选一个,补充在下面的横线上. 并加以解答.
在 △ABC 中,角 A , B , C 所对的边分别是 a , b , c ,且满足 .
(1)求角 C ;
(2)若 a= 4,b= 5,D在线段 AB 上,且满足 AD= 2 AB ,求线段 CD的长度.
5
16 (本小题满分 15分)
如图,四棱锥 P-ABCD 中,底面四边形 ABCD 为正方形,侧面 △PCD 是边长为 2 的正三角形, 若顶
点 P在底面的射影落在底边 CD上, M 在 BC 上且满足 AM = 1
2 AB+AC .
(1)求证: BC⊥PD;
(2)求二面角 C-PD-M 的大小.
25
宝剑锋从磨砺出
名校真题
17 (本小题满分 15分)
根据社会人口学研究发现,一个家庭有 X 个孩子的概率模型为:
X 1 2 3 0
P α α α 1-p α 1-p 2
p
其中 α> 0,0< p< 1 . 每个孩子的性别是男孩还是女孩的概率均为 1 且相互独立,事件 A
2 i
表示一个家
庭有 i 个孩子 i=0,1,2,3 ,事件 B 表示一个家庭的男孩比女孩多 (例如:一个家庭恰有一个男孩,则该
家庭男孩多).
(1)若 p= 1 ,求 α和 P B ;
2
(2)调控未来人口结构通过调控参数 p来进行,其中参数 p受到各种因素的影响 (例如生育保险的增加,
教育、医疗福利的增加等).
①若希望 P X=2 增大,如何调控 p的值
②是否存在 p的值使得 E X = 5 ,请说明理由.
3
18 (本小题满分 17分)
过抛物线 y2= 2px p>0 的对称轴上的定点 M m,0 m>0 ,作直线
AB 与抛物线相交于 A,B 两点.
(1)证明: A,B 两点的纵坐标之积为定值;
(2)若点 N 是定直线 l:x=-m 上的任一点,设直线 AN ,MN ,BN 的斜率分别为 k1,k2,k3 ,试探索 k1,k2,
k3 之间的关系,并证明.
26
梅花香自苦寒来
名校真题
19 (本小题满分 17分)
已知函数 f x = exsinx- cosx,g x = xcosx- 2ex ,其中 e是自然对数的底数.
(1)判断函数 y= f x π 在 0, 内零点的个数,并说明理由;2
(2)任意 x ∈ 0, π ,存在 x ∈ 0, π1 2
,使得不等式 f x1 + g x2 ≥m成立,试求实数 m的取值范围;2 2
(3)若 x>-1 ,求证: f x - g x > 0 .
27
宝剑锋从磨砺出
名校真题
名校经典真题汇编 (五)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知集合 M={x ∣ x= 3n- 2,n∈ Z},N={-2, -1,0,1,2} ,则 M∩N= ( )
A. {-2,1} B. {-1,2} C. {-1,1} D. {-2,0,2}
z i
2 已知复数 z满足 - - + = 1 ,则 z= ( )1 i 1 i
A. - 2+ i B. - 2- i C. 2+ i D. 2- i
3 若 e1,e2 是夹角为 60°的两个单位向量,则 a= 2e1+ e2 与 b=-3e1+ 2e2 的夹角为 ( )
A. 30° B. 60° C. 120° D. 150°
4 生物体死亡后,它机体内原有的碳 14含量 P会按确定的比率衰减 (称为衰减率), P与死亡年数
t
t a之间的函数关系式为 P= 1 (其中 a为常数), 大约每经过 5730年衰减为原来的一半, 这个时间称2
为“半衰期”. 若 2021年某遗址文物出土时碳 14的残余量约占原始含量的 75% ,则可推断该文物属于
( )
参考数据: log20.75≈-0.4
参考时间轴:
A. 宋 B. 唐 C. 汉 D. 战国
5 杭州亚运会共设 40个竞赛大项, 包括 31个奥运项目和 9个非奥运项目,共设杭州赛区、宁波赛
区、温州赛区、金华赛区、绍兴赛区、湖州赛区. 现需从 6名管理者中选取 4人分别到温州、金华、绍兴、湖
州四个赛区负责志愿者工作,要求四个赛区各有一名管理者,且 6人中甲、乙两人不去温州赛区,则不同
的选择方案共有 ( )
A. 300种 B. 240种 C. 144种 D. 96种
28
梅花香自苦寒来
名校真题
6 函数 f x = 2sin ωx+φ ω>0且0<φ<π 在一个周期内的图象如图所示,将函数 y= f x 图
象上的点的横坐标伸长为原来的 2倍,再向右平移 π 个单位长度,得到函数 y= g x 的图象,
4
则 g π = ( )3
A. 3 B. 1 C. - 1 D. - 3
7 在三棱锥 P-ABC 中, PA⊥平面 ABC,AB= 2,△ABC 与 △PAB 的外接圆圆心分别为 O1,O2
,若三棱锥 P-ABC 的外接球的表面积为 16π , 设 O1A= a,O2A= b ,则 a+ b的最大值是 ( )
A. 5 B. 10 C. 2 3 D. 2 5
8 如图 34- 5,矩形 ABCD的中心为 O,BC>AB ,现将 △DAC 沿着对角线 AC 翻折成 △EAC
. 记 ∠BOE= α ,二面角 B-AC-E 的平面角为 β ,直线 DE 与 BC 所成的角为 γ ,则 ( )
A. β> α,β> 2γ B. β> α,β< 2γ
C. β< α,β> 2γ D. β< α,β< 2γ
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
29
宝剑锋从磨砺出
名校真题
9 如图正方体 ABCD-A1B1C1D1 的棱长为 a ,以下结论正确的是 ( )
A. 异面直线 A1D与 AB1 所成的角为 60° B. 直线 A1D与 BC1 垂直
1
C. 直线 A1D与 BD1 平行 D. 三棱锥 A-A1CD的体积为 a36
10 已知 A,B 是抛物线 C:y2= 4x上两动点, F 为抛物线 C 的焦点,则 ( )
A. 直线 AB 过焦点 F 时, AB 最小值为 4
B. 直线 AB 过焦点 F 且倾斜角为 60°时 (点 A在第一象限), AF = 2 BF
C. 若 AB 中点 M 的横坐标为 3,则 AB 最大值为 8
D. 点 A坐标 (4,4),且直线 AF,AB 斜率之和为 0,AF 与抛物线的另一交点为 D ,则直线 BD方程为:
4x+ 8y+ 7= 0
11 已知函数 f x = xln 1+x ,则 ( )
A. f x 在 0,+∞ 单调递增 B. f x 有两个零点
C. 曲线 y= f x 在点 - 1 ,f - 1 处切线的斜率为 -1- ln2 D. f x 是偶函数2 2
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 过点 P 2,2 作圆 x2+ y2= 4的两条切线,切点分别为 A,B ,则直线 AB 的方程为 .
13 已知函数 f x = x2+ aln 2x+1 有两个不同的极值点 x1,x2 ,且 x1< x2 ,则实数 a的取值范
围是 .
30
梅花香自苦寒来
名校真题
定义离心率是 5-1
2 y2
14 的椭圆为“黄金椭圆”. 已知椭圆 E: x + = 1(10 >m> 0 )是“黄金
2 10 m
2 2
椭圆”,则 m= . 若“黄金椭圆”C: x + y = 1 a>b>0 两个焦点分别为 F1 -c,0 ,
a2 b2
F2 c,0 c>0 ,P为椭圆 C 上的异于顶点的任意一点,点 M 是 △PF1F2 的内心,连接 PM 并延长交 F1F2
PM
于点 N ,则 = . (第 1空 2分,第 2空 3分)
MN
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤.)
15 本小题满分 13分)
已知数列 an 中 a1= 1.M 1,1 ,An 2,an ,Bn 3,2a *n+1-3 为直角坐标平面上的点. 对任意 n∈N ,M、
An、Bn 三点共线.
(1)求数列 an 的通项公式;
(2)求证: 1 + 1 + 1 + + 1 < 3 .
a1a3 a2a4 a3a5 anan+2 4
16 (本小题满分 15分)
如图,在直角 △POA 中, PO⊥OA,PO= 2OA= 4 ,将 △POA 绕边 PO 旋转到 △POB 的位置,使
∠AOB= 90° ,得到圆锥的一部分,点 C 为 AB 上的点,且 AC = 1 AB
3
(1)求点 O到平面 PAB 的距离;
(2)设直线 PC 与平面 PAB 所成的角为 φ ,求 sinφ的值.
31
宝剑锋从磨砺出
名校真题
17 (本小题满分 15分)
某工厂为了提高生产效率, 对生产设备进行了技术改造, 为了对比技术改造后的效果, 采集了技术改造
前后各 20次连续正常运行的时间长度 (单位:天)数据,整理如下:
改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21;
改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36.
(1)完成下面的列联表,并依据小概率值 α= 0.010 的独立性检验分析判断技术改造前后的连续正常运
行时间是否有差异
技术改造 设备连续正常运行天数 合计
超过 30 不超过 30
改造前
改造后
合计
(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费和保障维护
费两种. 对生产设备设定维护周期为 T 天 (即从开工运行到第 kT 天, k∈N * )进行维护. 生产设备在一
个生产周期内设置几个维护周期, 每个维护周期相互独立. 在一个维护周期内, 若生产设备能连续运行,
则只产生一次正常维护费, 而不会产生保障维护费; 若生产设备不能连续运行, 则除产生一次正常维护
费外,还产生保障维护费.经测算,正常维护费为 0.5 万元 / 次, 保障维护费第一次为 0.2 万元 /周期, 此
后每增加一次则保障维护费增加 0.2万元.
现制定生产设备一个生产周期 (以 120 天计) 内的维护方案: T= 30,k= 1,2,3,4 . 以生产设备在技术改
造后一个维护周期内能连续正常运行的频率作为概率, 求一个生产周期内生产维护费的分布列及均值.
附:
α 0.15 0.10 0.05 0.025 0.010 0.005 0.001
xα 2.072 2.706 3. 841 5.024 6.635 7. 879 10.828
n ad-bc 2
χ2= , 其中n=a+b+c+d .
a+b c+d a+c b+d
32
梅花香自苦寒来
名校真题
18 (本小题满分 17分)
2 2
设 A,B 为双曲线 C: x - y = 1 a>0,b>0 的左、右顶点,直线 l过右焦点 F 且与双曲线 C 的右支交
a2 b2
于 M ,N 两点,当直线 l垂直于 x轴时,
△AMN 为等腰直角三角形.
( 1 )求双曲线 C 的离心率;
(2)已知 AB= 4 ,若直线 AM ,AN 分别交直线 x= a 于 P,Q 两点,当直线 l 的倾斜角变化时,以 PQ
2
为直径的圆是否过定点 若过定点, 求出定点的坐标;若不过定点, 请说明理由.
19 (本小题满分 17分)
2
已知 e是自然对数的底数,函数 f x = ax ,直线 y= 1 x为曲线 y=
ex e
f x 的切线, g x = x+1 lnx .
(1)求 a的值;
(2)① 判断 F x = f x - g x 的零点个数;
m,m≤n,
② 定义 min{m,n}= 函数 m x =min f x ,g x .n,m>n,
h x =m x - tx2 在 0,+∞ 上单调递增. 求实数 t的取值
范围.
33
宝剑锋从磨砺出
名校真题
名校经典真题汇编 (六)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知集合 A={x ∣-1< x≤ 4},B= x∣ x-2a x-a2-1 <0 , 若 A∩B= ,则实数 a的取
值范围为 ( )
A. {a ∣ a> 2} B. {a ∣ a≥ 2}
C. {a ∣ a= 1或 a≥ 2} D. {a ∣ a≥ 1}
2 已知复数 z1,z2 满足 z2≠ 0, z1 z2 = 2 z2 ,则 z1 = ( )
A. 2 . B. 2 C. 2 2 D. 4
3 在 △ABC 中,点 N 满足 AN = 2NC ,记 BN = a,NC = b ,那么 BA= ( )
A. a- 2b B. a+ 2b C. a- b D. a+ b
4 已知 a= lg 1 ,b= 20.1,c= sin3 ,则 ( )
2
A. a> b> c B. b> c> a C. b> a> c D. c> b> a
5 2022年 9月 16日,迎接第九批在韩志愿军烈士遗骸回国的运一 20专机在两架歼一 20战斗机
护航下抵达沈阳国际机场. 歼一 20战机是我国自主研发的第五代最先进的战斗机, 它具有高隐身性、高
态势感知、高机动性能等特点, 歼一 20机身头部是一个圆锥形, 这种圆锥的轴截面是一个边长约为 2米
的正三角形,则机身头部空间大约 ( )立方米
3 2
A. 3π B. π C. 2π D. π
3 2
6 已知函数 f x = cos ωx- π - 1 ω>0 ,将 f x 的图象上所有点的横坐标缩短为原来的 13 2 2
,纵坐标不变,得到函数 g x 的图象,已知 g x 在 0,π 上恰有 5个零点,则 ω的取值范围是 ( )
2, 8 7 8 7A. B. 2, C. 2, 3 3 3 D. 2, 3
34
梅花香自苦寒来
名校真题
7 用 1,2,3,4,5,6组成六位数 (没有重复数字),在任意相邻两个数字的奇偶性不同的条件下, 1和 2
相邻的概率是 ( )
5 4 5 13
A. B. C. D.
18 9 9 18
8 已知直三棱柱 ABC-A1B1C1 中, AB=AA1= 2,BC= 3AC ,当该三棱柱体积最大时, 其外接
球的体积为 ( )
28 21 32 20 5 28 7
A. π B. π C. π D. π
27 3 3 9
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选项中, 有多项符合题目要求. 全部
选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9
例1 (2023 新高考)下列物体中,能够被整体放入棱长为 1(单位:m)的正方体容器 (容器壁厚度忽略不计)
内的有 ( )
A. 直径为 0.99m的球体 B. 所有棱长均为 1.4m的四面体
C. 底面直径为 0.01m,高为 1.8m的圆柱体 D. 底面直径为 1.2m,高为 0.01m的圆柱体
10 已知抛物线 C:y= 1 x2 的焦点为 F,P为 C 上一点,下列说法正确的是 ( )
4
A. C 的准线方程为 y=- 1 B. 直线 y= x- 1与 C 相切
16
C. 若 M 0,4 ,则 PM 的最小值为 2 3 D. 若 M 3,5 ,则 △PMF 的周长的最小值为 11
11 已知偶函数 f x 在 R上可导, f 0 =-1,g x = f x ,若 f x+1 -f 1-x = 2x ,则 ( )
A. g 0 = 0 B. g 2023 = 2023
C. f 3 = 3 D. f -2n = 2n2- 1 n∈N
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 设多项式 x+1 6 + x-1 1 0= a x1010 + a9x9+ +a1x+ a0 ,则 a0+ a2 +a4+ a6+ a8+ a10=
.
35
宝剑锋从磨砺出
名校真题
2 y2
13 已知点 F1 是椭圆
x + = 1 a>b>0 的左焦点,过原点作直线 l交椭圆于 A,B 两点, M ,N
a2 b2
分别是 AF1,BF1 的中点,若存在以 MN 为直径的圆过原点,则椭圆的离心率的范围是 .
14 设函数 f x = 3 x2- 2ax a>0 的图象与 g x = a2lnx+ b的图象有公共点,且在公共点处切
2
线方程相同,则实数 b的最大值为 .
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤.)
15 (本小题满分 13分)
在数列 an 中, a1= 1 ,其前 n项和为 Sn ,且满足 an 2Sn-1 = 2S2n n∈N *,n≥2 .
(1)求证:数列 1 Sn
是等差数列;
(2)证明:当 n≥ 2时, S1+ 1 S 1 1 32 2+ S3 3+ + Sn n< .2
16 (本小题满分 15分)
如图,在直四棱柱 ABCD-A1B1C1D1 中,底面 A1B1C1D1 是梯形,且 A1B1 D1C1,A1D1=D1D=D1C1=
1 A B = 1,AD
2 1 1 1
⊥A1C,E 是棱 A1B1 的中点.
(1)求证: CD⊥AD;
(2)求点 C1 到平面 CD1B1 的距离;
(3)求二面角 D1-CE-B1 的余弦值.
36
梅花香自苦寒来
名校真题
17 (本小题满分 15分)
2 y2
已知双曲线 C : x - = 1 a>0,b>0 经过点 (2, - 3),两条渐近线的夹角为 60° ,直线 l 交双曲线 C
a2 b2
于 A,B 两点.
( 1 )求双曲线 C 的方程;
(2)若动直线 l 经过双曲线的右焦点 F2 ,是否存在 x 轴上的定点 M (m , 0) ,使得以线段 AB 为直径的
圆恒过 M 点 若存在,求实数 m的值;若不存在, 请说明理由.
18 (本小题满分 17分)
某中学 2022 年 10 月举行了 2022“翱翔杯”秋季运动会,其中有“夹球跑”和“定点投篮”两个项目, 某班
代表队共派出 1 男 (甲同学) 2 女 (乙同学和丙同学)三人参加这两个项目, 其中男生单独完成“夹球跑”
的概率为 0.6,女生单独完成“夹球跑”的概率为 a 0
(1)证明:在 ξ的概率分布中, P ξ=1 最大;名校经典真题汇编 (六) - 6
(2)对于“定点投篮”项目,比赛规则如下:该代表队先指派一人上场投篮,如果投中,则比赛终止,如果没
有投中,则重新指派下一名同学继续投篮, 如果三名同学均未投中, 比赛也终止. 该班代表队的领队了解
后发现,甲、乙、丙三名同学投篮命中的概率依次为 ti= P ξ= i i=1,2,3 ,每位同学能否命中相互独立.
请帮领队分析如何安排三名同学的出场顺序, 才能使得该代表队出场投篮人数的均
值最小 并给出证明.
37
宝剑锋从磨砺出
名校真题
19 (本小题满分 17分)已知函数 f x = sinx- x+mlnx,m≠ 0 .
(1)若函数 f x 在 0,+∞ 上是减函数,求 m的取值范围;
(2)设 α∈ π, 3π ,且满足 cosα= 1+ αsinα ,证明:当 0
38
梅花香自苦寒来
名校真题
名校经典真题汇编 (七)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知集合 A={x ∣ y= lnx},B= y∣y=ex-1 ,则 A∪B= ( )
A. R B. [0, +∞) C. -1,+∞ D.
2 已知复数 z满足 1- i z= 2+ 2i ,则 z的共轭复数 z= ( )
A. 2 B. - 2 C. 2i D. - 2i
3 若 tanα= 1 ,则 sin2α- cos2α= ( )
A. - 1 1 1B. C. D. 1
5 4 2
4 已知 A -3,0 ,B 3,0 ,C 0,3 ,一束光线从点 F -1,0 出发经 AC 反射后,再经 BC 上点 D反
射,落到点 E 1,0 上. 则点 D的坐标为 ( )
A. 1 , 5 3 3B. ,2 2 2 2 C. (1,2) D. (2,1)
5 已知 a= ln π ,b= 2 π - 2,c= 2tan π -1 ,则 a,b,c的大小关系是 ( )3 3 3
A. c> b> a B. a> b> c C. b> a> c D. a> c> b
6 为参加学校组织的“喜迎二十大,奋进新征程”的演讲比赛,某班从班级初选的甲、乙 2名男生和
6名女生共 8名同学中随机选取 5名组成班级代表队参加比赛, 则代表队中既有男生又有女生的条件
下, 男生甲被选中的概率为 ( )
15 5 1 7
A. B. C. D.
56 7 2 10
39
宝剑锋从磨砺出
名校真题
2 2
7 已知椭圆 C: x + y = 1 a>b>0 的左、右焦点分别为 F ,F
2 2 1 2
,P为 C 上不与左、右顶点重合的
a b
一点, I 为 △PF1F2 的内心,且 3IF1+ 2IF2= 2PI ,则 C 的离心率为 ( )
1 2 3 6
A. B. C. D.
3 5 3 5
8 已知函数 f x = 3lnx- x3ex+ 1 ,若存在 x0> 0 ,使 f x0 ≥ ax0 ,则 a的最大值为 ( )
A. 0 B. - 1 C. 1- e D. 1- e2
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
1
9 已知数列 an 满足 a1= ,an+1=
2an n∈N *+ ,则下列结论正确的是 ( )3 2an 1
A. 1 -2 为等比数列an
n-1
B. an 的通项公式为 a
2
n=
2n+1
C. an 为递减数列
D. 1 的前 n项和 Tn= 2n+ 1- 2-nan
10 已知函数 f x = ex- x,g x = x- lnx ,则下列说法正确的是 ( )
A. f lnx 在 1,+∞ 上是增函数
B. x> 1 ,不等式 f ax ≥ f lnx2 恒成立,则正实数 a的最小值为 2
e
C. 若 g x = t有两个零点 x1,x2 ,则 x1 x2> 1
D. 若 f x1 = g lnt 1 x2 = t t>2 ,且 x2> x1> 0 ,则 - 的最大值为x2 x1 e
2 y2
11 已知 F1,F x2 分别为双曲线 C: - = 1 a>0,b>0 的左、右焦点,点 M 为双曲线右支上一
a2 b2
点,设 ∠F1MF2= θ . 过 M 作两渐近线的垂线,垂足分别为 P,Q ,则下列说法正确的是
2
A. F2M 的最小值为
b
a
B. MP MQ 为定值
40
梅花香自苦寒来
名校真题
C. 若当 θ= π 时, △OMF2 ( O为坐标原点)恰好为等边三角形,则双曲线 C 的离心率为 3+ 12
D. 当 θ= π 时,若直线 F1M 与圆 x2+ y2= a2 相切,则双曲线 C 的渐近线的斜率的绝对值为 3- 36
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 如图,在直角梯形 ABCD中, AD BC,AB⊥BC , AD= 1,BC= 2,P是线段 AB 上的动点,
则 PC+4PD 的最小值为 .
13 党的二十大是在全党全国各族人民迈上全面建设社会主义现代化国家新征程, 向第二个百年奋
斗目标进军的关键时刻召开的一次十分重要的大会. 在二十大即将胜利召开之际, 某学校组织了《喜迎
二十大,谱写新篇章》的演讲比赛,本次比赛的冠军奖杯由一个铜球和一个托盘组成,如图 1. 已知球的
表面积为 20π ,托盘由边长为 4 3 的正三角形 △ABC 铜片沿各边中点的连线垂直向上折叠而成,如图
2, 则球心离底面 DEF 的距离为 .
图 1
图 2
14 已知定义在 N * 上的单调递增函数 y= f x ,对于任意的 n∈N * ,都有 f n ∈N * ,且 f f n
= 3n恒成立,则 f 2023 = .
41
宝剑锋从磨砺出
名校真题
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤.)
15 (本小题满分 13分)
记 △ABC 的内角 A,B,C 的对边分别为 a,b,c . 已知 b = cosB .
c 2-cosC
(1)求 a ;
b
(2)若 cosC= 1 ,AB 边上的中线 CD= 6 ,求 △ABC 的面积.
4
16 (本小题满分 15分)
如图,在四棱锥 P-ABCD 中, PA⊥ 平面 ABCD,PA=AB=BC= 3 , AD=CD= 1,∠ADC= 120°
,点 M 是 AC 与 BD的交点,点 N 在线段 PB 上,且 PN= 1 PB .
4
(1)证明: MN 平面 PDC ;
(2)在线段 BC 上是否存在一点 Q ,使得平面 MNQ⊥ 平面 PAD ?若存在,求出点 Q 的位置; 若不存
在,请说明理由.
42
梅花香自苦寒来
名校真题
17 (本小题满分 15分)
在直角坐标系 xOy中,动圆 P 与圆 Q: x-1 2 + y2= 1外切,且圆 P 与 y轴相切,记动圆圆心 P 的轨迹
为曲线 C .
( 1 )求曲线 C 的轨迹方程;
(2)设过定点 S -1,0 的动直线 l 与曲线 C 交于 A,B 两点,试问: 在曲线 C 上是否存在点 M (与 A,B
两点相异),当直线 MA,MB 的斜率存在时,直线 MA,MB 的斜率之和为定值 若存在,求出点 M 的坐
标;若不存在, 请说明理由.
18 (本小题满分 17分)
甲乙两人进行乒乓球比赛, 经过以往的比赛分析, 甲乙对阵时, 若甲发球,则甲得分的概率为 3 ,若乙发
5
球,则甲得分的概率为 1 . 该局比赛甲
3
乙依次轮换发球权 (甲先发球), 每人发两球后轮到对方进行发球.
(1)求在前 4球中,甲领先的概率;
(2) 12球过后,双方战平 6:6 ,已知继续对战奇数球后,甲率先取得 11分获得胜利 (获胜要求净胜 2分
及以上),设净胜分为 X (甲,乙的得分之差),求 X 的分布列.
43
宝剑锋从磨砺出
名校真题
19 (本小题满分 17分)
设函数 f x = x2- ax- a2ln x. a∈R
(1)当 a= 2时,讨论函数 y= f x 的单调性;
(2)若 a≠ 0 ,曲线 y= f x 与直线 y=m交于 A x1,y1 ,B x2,y2 两
, : x1+x点 求证 f 2 > 0 ;2
(3)证明: 1 + 1 + + 1 < 1 lnn n≥2,n∈N * .
3 5 2n-1 2
44
梅花香自苦寒来
名校真题
名校经典真题汇编 (八)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知集合 A={x∈ Z ∣ x< 2},B= x∣x2-2x-3<0 ,则 A∩B= ( )
A. {-1,0,1,2} B. {0,1} C. {-1,0,1} D. {-2,0,1}
z
2 已知复数 z在复平面内对应的点的坐标为 (-1,2),则
1+ = ( )i
- 3 + 3 3 1 3 3 1 3A. i B. - - i C. - - i D. + i
2 2 2 2 2 2 2 2
3 已知曲线 y= 4 x 在点 (1,4)处的切线的倾斜角为 α ,则 1+sinα+cosα = ( )
2 1- 2cos α+ π4
2 2 2 1A. B. C. D. 1 .
2 2
4 深度学习是人工智能的一种具有代表性的实现方法, 它是以神经网络为出发点的,在神经网络优
G
化中,指数衰减的学习率模型为 L=L σ00D ,其中 L表示每一轮优化时使用的学习率, L0 表示初始学习
率, D表示衰减系数, G 表示训练迭代轮数, G0 表示衰减速度. 已知某个指数衰减的学习率模型的初始
学习率为 0.5 , 衰减速度为 18 , 且当训练迭代轮数为 18时,学习率衰减为 0.4 ,则学习率衰减到 0.2以
下 (不含 0.2 )所需的训练迭代轮数至少为 参考数据:lg2≈0.3010 ( )
A. 72 B. 74 C. 76 D. 78
5 已知 x-1 4 + 2x5= a0+ a1 x+1 + a2 x+1 2 + +a5 x+1 5 ,则 a2= ( )
A. - 2 B. 2 C. 4 D. 12
f x2 - f x
6 已知函数 f x 满足 f -x =-f x ,且对任意的 x1,x2∈ [0, +∞) , x1≠ x2 ,
1
都有
x2-x1
> 2,f 1 = 2020 ,则满足不等式 f(x- 2020)> 2 x-1011 的 x的取值范围是 ( )
A. 2021,+∞ B. 2020,+∞ C. 1011,+∞ D. 1010,+∞
45
宝剑锋从磨砺出
名校真题
7 某人造地球卫星的运行轨道是以地心为一个焦点的椭圆, 其轨道的离心率为 e ,设地球半径为 R
,该卫星近地点离地面的距离为 r ,则该卫星远地点离地面的距离为 ( )
1+e r+ 2e R 1+e e 1+e 2e 1-e eA. - B. r+ R C. r+ R D. r+ R1-er 1 e 1-e 1-e 1-e 1+e 1+e 1+e
8 若实数 x,y满足 4lnx+ 2lny≥ x2+ 4y- 4 ,则 ( )
A. xy= 2 B. x+ y= 2 C. 2x+ y= 1+ 2 D. x3y= 1
2
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 已知 OA,OB 是平面内两个夹角为 120°的单位向量,点 C 在以 O为圆心的 AB 上运动 (包括
A,B 两点),若 OC = xOA+ yOB x,y∈R . 下列说法正确的有 ( )
A. 当 C 位于 AB 中点时, x= y= 1
B. 当 C 位于 AB 中点时, x+ y的值最大
C. OC 在 OA上的投影向量的模的取值范围为 1 ,1
2
3 3
D. OC OA-OB 的取值范围为 - ,
2 2
10 在正方体 ABCD-A1B1C1D1 中, E、F、G 分别为 BC、CC1、BB1 的中点, 则 ( )
A. 直线 A1D与直线 EF 垂直
B. 点 C 与点 G 到平面 AEF 的距离相等
C. 直线 A1G 与平面 AEF 不平行
D. 过 A、E、F 三点的平面截正方体的截面为等腰梯形
46
梅花香自苦寒来
名校真题
ω
11 已知 f x = 2cos2 x+φ - 1 ω>0,φ∈ 0, π 具有下面三个性质:①将 f x 的图象右移 π2 4
个单位得到的图象与原图象重合;② x∈R , f 5π 5π x ≤ f ;③ f x 在 x∈ 0,12 12 时存在两个零
点. 给出下列判断,其中正确的是 ( )
π
A. f x 在 x∈ 0, 时单调递减4
B. f π + f π + f48 3
9π = 1
16 2
π
C. 将 f x 的图象左移 个单位长度后得到的图象关于原点对称
24
若 g π π 2πD. x 与 f x 的图象关于 x= 对称,则当 x∈ ,
时, g x 的值域为
-1, 1 3 2 3 2
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 由 1,2,3,4,5,6组成的没有重复数字的六位数,要求奇数 1,3,5两两不相邻,但 1和 2必须相邻,
这样的六位数共有 个.
13 已知函数 f x = log 1 -x2+2x+t 的定义域是 m,m+4 ,则函数 f x 的单调递增区间为
2
.
14 点 M 是圆 C:x2+ y2= 1上一个动点,直线 l1:mx-ny- 3m+n= 0与直线 l2:nx+my- 3m-
n= 0 m,n∈R,m2+n2≠0 相交于点 P ,则 PM 的取值范围是 ;
2 y2
若双曲线 x - = 1 a>0,b>0 的一条渐近线过点 P ,则双曲线的离心率的最大值为 . (第 1
a2 b2
空 2分, 第 2空 3分)
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤.)
15 (本小题满分 13分)
已知 Sn 是等差数列 an 前 n项和, S9= 81,a6+ a8= 26 .
(1)求 an 的通项公式;
(2)在 an 中,去掉以 a1 为首项,以 a2 为公比的数列的项,剩下的项按原来顺序构成的数列记为 bn ,
求 bn 前 100项和 T100 .
47
宝剑锋从磨砺出
名校真题
16 (本小题满分 15分)
如图,在四棱锥 P-ABCD 中,底面 ABCD 为直角梯形,其中 AD BC,AB⊥AD,AD= 3,AB= BC
= 2,PA⊥平面 ABCD ,且 PA= 3 ,点 M 在棱
PD上,点 N 为 BC 中点.
(1)证明:若 DM= 2MP ,则直线 MN 平面 PAB ;
(2)求二面角 C-PD-N 的正弦值;
(3)是否存在点 M ,使 NM 与平面 PCD所成角的正弦值为 2 ?若存在,求出 PM 的值;若不存在,
6 PD
说明理由.
17 (本小题满分 15分)
为了有针对性地提高学生体育锻炼的积极性, 教育集团需要了解性别因素是否对学生体育锻炼的经常
性有影响, 为此随机抽查了男女生各 100名, 得到如下数据:
性别 锻炼
不经常 经常
女生 40 60
男生 20 80
(1)依据 α= 0.01的独立性检验,能否认为性别因素与学生体育锻炼的经常性有关系
(2)从这 200人中随机选择 1人,已知选到的学生经常参加体育锻炼, 求他是男生的概率;
(3)为了提高学生体育锻炼的积极性, 集团设置了“学习女排精神, 塑造健康体魄”的主题活动,在该活动
的某次排球训练课上,甲乙丙三人相互做传球训练, 第 1 次由甲将球传出, 每次传球时, 传球者都等可能
地将球传给另外两个人中的任何一人. 求第 n次传球后球在甲手中的概率.
n ad-bc 2: 2= 附 χ
a+b c+d a+c b+d
48
梅花香自苦寒来
名校真题
α 0.010 0.005 0.001
xα 6.635 7. 879 10.828
18 (本小题满分 17分)
x2: + y
2 2
设椭圆 E = 1 a>b>0 的左右焦点 F ,F 分别是双曲线 x - y21 2 = 1 的左右顶点,且椭圆的右
a2 b2 4
顶点到双曲线的渐近线的距离为 2 10 .
5
(1)求椭圆 E 的方程;
(2)是否存在圆心为原点的圆,使得该圆的任意一条切线与椭圆 E 恒有两个交点 A,B ,且 OA⊥OB
若存在,写出该圆的方程,并求 AB 的取值范围;若不存在,请说明理由.
49
宝剑锋从磨砺出
名校真题
19 (本小题满分 17分)
已知函数 f x = x+a 2 + blnx,a,b∈R且 b≠ 0 .
(1)若直线 y= 2ax是曲线 y= f x 的切线,求 a2- b的最小值;
f x
( ) 1
- f x
2 2设 b= 1 ,若函数 f x 有两个极值点 x1 与 x2 ,且 x1< x 22 ,证明 - > a- .x1 x2 a
50
梅花香自苦寒来
名校真题
名校经典真题汇编 (九)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知集合 A= y∣y= x-1 -1,x∈R ,B= x∣log3x≥1 ,则 A∩ RB= ( )
A. {x ∣ x≥-1} B. {x ∣ x< 3} C. {x ∣-1≤ x≤ 3} D. {x ∣-1≤ x< 3}
2 设复数 z1,z2 在复平面内的对应点关于实轴对称, z1= 1+ i ,则 z1z2= ( )
A. 2 B. - 2 C. 1+ i D. 1- i
3 已知函数 f x = 2cosx- f π sinx ,则 f π = ( )3 3
2 3 2 3
A. B. - C. 2 D. - 2
3 3
4 在双曲线中,虚轴长为 6,且双曲线与椭圆 x2+ 16y2= 16有公共焦点,则双曲线的方程是
( )
x2 y2 2 y2 y2 2 y2 2
A. - = 1 xB. - = 1 x xC. - = 1 D. - = 1
9 6 6 9 9 6 6 9
5 已知向量 a= -1,m m>0 ,b= 4,3 ,且 a = b ,则 a b= ( )
A. 68 B. - 68 C. - 4- 6 6 D. 6 6- 4
6 为了解某种产品与原材料之间的关系, 随机调查了该产品 5个不同时段的产品与原材料的价格,
得到如下统计数据表:
原材料价格 1 1.2 1.4 1.6 1.8
x (万元 /
吨)
产品价格 y 5 5.8 k 8.1 8.8
(万元 /件)
51
宝剑锋从磨砺出
名校真题
但是统计员不小心丢失了一个数据 (用 k 代替),在数据丢失之前得到经验回归方程为 y= 5x- 0.04 ,
则 k的值等于 ( )
A. 7.1 B. 7.2 C. 7.3 D. 7.4
6 4
7 x+1- 2 的展开式中, x 的系数为 ( )y y2
A. 60 B. - 60 C. 120 D. - 120
8 三棱锥 A-BCD中, AB=BC=AD=CD=BD= 2 3 ,AC= 3 3 ,则三棱锥 A-BCD的外
接球的表面积为 ( )
A. 20π B. 28π C. 32π D. 36π
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 记函数 f x = cos ωx+ π ω>0 的最小正周期为 T ,且 2nπ ≤T≤nπ n∈N * . 若 x= π 4 3 6
为 f x 的零点,则 ( )
2
A. ≤ω≤ 3 B. ω< 3
n n 2n-1
x= π 为 f x 7πC. 的零点 D. x= 为 f x 的极值点
2 6
52
梅花香自苦寒来
名校真题
10 抛物线 y2= 4x的焦点为 F ,过 F 的直线交抛物线于 A,B 两点,点 P在抛物线 C 上,则下列
结论中正确的是 ( )
16
A. 当 AF = 3FB 时, AB =
3
B. 若 M 2,2 ,则 PM + PF 的最小值为 4
PQ
C. 若 Q -1,0 ,则 的取值范围为 1, 2
PF
D. 在直线 x=- 3 上存在点 N ,使得 ∠ANB= 90°
2
11 在平面凸四边形 ABCD中, △ABD的面积是 △BCD面积的 2倍,又数列 an 满足 a1= 2 ,恒
有 BD= a -2n-1n BA+ a nn+1+2 BC ,设 an 的前 n项和为 Sn ,则 ( )
a
A. an 为等比数列 B. n 为等差数列 C. an 为递增数列 D. Sn= 3-n 2n+1- 62n
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 已知甲、乙两组按从小到大顺序排列的数据:
甲组: 27,28,37,m,40,50 ;
乙组: 24,n,34,43,48,52 .
若这两组数据的第 30百分位数、第 50百分位数分别对应相等, 则 n = .
m
13 若 a> b> 1 ,且 a+ 3b= 5 ,则 1 4 2- + - 的最小值为 , ab- b - a+ b的最大值为a b b 1
. (本题第 1空 2分, 第 2空 3分)
14 在四棱锥 P-ABCD中,底面 ABCD是边长为 2的正方形,平面 PAB⊥平面 PCD ,则 P-
ABCD体积的最大值为 .
53
宝剑锋从磨砺出
名校真题
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤.)
15 (本小题满分 13分).
在 △ABC 中,内角 A,B,C 的对边分别是 a,b,c . 已知 asinA+ bsinB- csinC= 3bsinA .
(1)求角 C 的大小;
(2)若 b= 32 ,c= 2 ,求 △ABC 的面积.
17
16 (本小题满分 15分)三棱台 ABC-A1B1C1 的底面是正三角形, AA1⊥平面 ABC,AB= 4,A1B1
= 2,AA1= 3 , E 是 AB 的中点,平面 A1C1E 交平面 ABC 于直线 l .
(1)求证: AC l;
(2)求直线 B1C 与平面 A1C1E 所成角的正弦值.
54
梅花香自苦寒来
名校真题
17 (本小题满分 15分)
2020年以来, 新冠疫情对商品线下零售影响很大. 某商家决定借助线上平台开展销售活动. 现有甲、乙两
个平台供选择, 且当每件商品的售价为 a 300≤a≤500 元时,从该商品在两个平台所有销售数据中各
随机抽取 100天的日销售量统计如下:
商品日销售 6 7 8 9 10
量 (单位:
件)
甲平台的天 14 26 26 24 10
数
乙平台的天 10 25 35 20 10
数
假设该商品在两个平台日销售量的概率与表格中相应日销售量的频率相等,且每天的销售量互不影响.
(1)求“甲平台日销售量不低于 8件”的概率, 并计算“从甲平台所有销售数据中随机抽取 3天的日销售
量, 其中至少有 2天日销售量不低于 8件”的概率;
(2)已知甲平台的收费方案为:每天佣金 60 元,且每销售一件商品,平台收费 30 元; 乙平台的收费方案
为:每天不收取佣金,但采用分段收费, 即每天销售商品不超过 8件的部分, 每件收费 40元, 超过 8件的
部分, 每件收费 35 元. 某商家决定在两个平台中选择一个长期合作,从日销售收入 (单价 ×日销售量一
平台费用)的期望值较大的角度, 你认为该商家应如何决策 说明理由.
C: CTIVE: CTIVE: CTIVE: CTIVE: CTIVE: CTIV名校经典真题汇编 (九) - 6
18 (本小题满分 17分)
x2 y2已知双曲线 C: - = 1 a>0,b>0 的右焦点为 F ,双曲线 C 上一点
a2 b2
P 3,1 关于原点的对称点为 Q ,满足 FP FQ= 6 .
(1)求 C 的方程;
(2)直线 l与坐标轴不垂直,且不过点 P 及点 Q ,设 l与 C 交于 A , B 两点,点 B 关于原点的对称点为
D ,若 PA⊥PD ,证明:直线 l的斜率为定值.
55
宝剑锋从磨砺出
名校真题
19 (本小题满分 17分)
已知函数 f x = ax2+ lnx,g a x = 2x+ lnx ,其中 a∈R .
2
(1)若 f x ≥ g x ,求实数 a的取值范围;
( x2)记 f x 的零点为 x1,x2 x1
56
梅花香自苦寒来
名校真题
名校经典真题汇编 (十)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 已知集合 A={1,2},B={2,3} ,则集合 C={z ∣ z= x+ y,x∈A,y∈B}的真子集个数为
( )
A. 5 B. 6 C. 7 D. 8
2 设 b,c∈R ,若 2- i (i为虚数单位)是一元二次方程 x2+ bx+ c= 0的一个虚根, 则 ( )
A. b= 4,c= 3 B. b= 4,c= 5 C. b=-4,c= 3 D. b=-4,c= 5
3 如图,在 △ABC 中,点 D是边 BC 的中点, AG= 2GD ,则用向量 AB,AC 表示 BG 为
A. BG=- 2 AB+ 1 AC
3 3
B. BG=- 1 AB+ 2 AC
3 3
C. BG= 2 AB- 1 AC
3 3
D. BG= 2
AB+ 1 AC
3 3
4 斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”,它的画法是:以斐波那契数 1,1,2,3,5, 8,
为边长比例的正方形拼成矩形,然后在每个正方形中画一个圆心角为 90°的圆弧,这些圆弧所连起来的
弧线就是斐波那契螺旋线. 如图,矩形 ABCD是由若干符合上述特点的正方形拼接而成,其中 AB =
16 ,则图中的斐波那契螺旋线的长度为 ( )
57
宝剑锋从磨砺出
名校真题
A. 11π B. 12π C. 15π D. 16π
1 1
5 设 a= ln2,b= 2 2 ,c= 3 3 ,则 a,b,c的大小关系为 ( )
A. c< a< b B. b< a< c
C. a< c< b D. a< b< c
6 已知函数 f x = sin ωx+φ ω>0, φ < π 在区间 π , 7π2 6 6 上单调,且对任意实数 x均有
f 7π ≤ f π x ≤ f6 成立,则 φ= ( )6
π π π π
A. B. C. D.
12 6 4 3
7 如图,已知四棱柱 ABCD-A1B1C1D1 的体积为 V ,四边形 ABCD是平行四边形,点 E 在平面
ACC1A1 内,且 AE= 1 AC + 3 AC1 ,则三棱锥 D1 -ADC 与三棱锥 E-BCD的公共部分的体积为4 4
( )
V V 3V V
A. B. C. D.
28 21 28 7
58
梅花香自苦寒来
名校真题
2 2
8 已知椭圆 C: x + y = 1 a>b>0 的左、右焦点分别是 F1 -c,0 ,F2(c , 0) ,若离心率 e=
a2 b2
5-1
e≈0.618 ,则称椭圆 C 为“黄金椭圆”. 则下列三个命题中正确命题的个数是 ( )
2
① 在黄金椭圆 C 中, b2= ac;
②在黄金椭圆 C 中,若上顶点、右顶点分别为 E,B ,则 ∠F1EB= 90° ;
③ 在黄金椭圆 C 中,以 A -a,0 ,B a,0 ,D 0,-b ,E 0,b 为顶点的菱形 ADBE 的内切圆过焦点 F1,F2
.
A. 0 B. 1 C. 2 D. 3
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 上级某部门为了对全市 36000名初二学生的数学水平进行监测, 将获得的样本 (数学水平分数)
数据进行整理分析,全部的分数可按照 [50,60) ,
[60,70),[70,80),[80,90), 90,100 分成 5 组,得到如图所示的频率分布直方图. 则下列说法正确的是
( )
A. 图中 x的值为 0.025
B. 估计样本数据的 80%分位数为 84
C. 由样本数据可估计全市初二学生数学水平分数低于 60分的人数约为 360
D. 由样本数据可估计全市初二学生数学水平分数 80分及以上的人数占比为 3%
59
宝剑锋从磨砺出
名校真题
10 (多选)我国著名数学家华罗庚先生曾说:“数缺形时少直观,形少数时难入微.数形结合百般好,
割裂分家万事休.”在数学的学习和研究中,常用两数的图像来研究函数的性质,也常用函数的解析式琢
x
磨函数图象的特征,如函数 y= xa (a> 0且 a≠ 1)的图像的大致形状可能是 ( )
x
A. B.
C. D.
11 如图,正四棱锥 E-ABCD的底面边长与侧棱长均为 a ,正三棱锥 F-ADE 的棱长均为 a ,
则 ( )
A. EF⊥BC
B. 正四棱锥 E-ABCD的内切球半径为 1- 2 a2
C. E,F,A,B 四点共面
D. 平面 FAD 平面 BEC
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
5
12 2x+1 1 x- 的展开式中含 x4 项的系数为 .x
13 已知直线与抛物线 y2= 2px p>0 交于 A,B 两点, 且 OA⊥OB,OD⊥AB 交 AB 于点 D ,点
D的坐标为 (1,2),则 △AOB 的面积 = .
60
梅花香自苦寒来
名校真题
14 若方程 x2e-x= ax- lnx- 1存在唯一实根,则实数 a的取值范围为 .
四:解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演 算步骤.)
15 本小题满分 13分)
记 △ABC 的内角 A,B,C 的对边分别为 a,b,c ,已知 sinCsin A-B = sinBsin C-A .
(1)证明: 2a2= b2+ c2 ;
(2)若 a= 5,cosA= 25 ,求 △ABC 的周长.
31
16 (本小题满分 15分)
如图,在底面是菱形的四棱锥 P-ABCD中, PA⊥平面 ABCD,∠ABC= 60°,PA=AB= 2 ,点 E,F 分
别为 BC,PD的中点,设直线 PC 与平面 AEF 交于点 Q .
(1)已知平面 PAB∩平面 PCD= l ,求证: AB l;
(2)求直线 AQ与平面 PCD所成角的正弦值.
61
宝剑锋从磨砺出
名校真题
17 (本小题满分 15分)
如图,平面直角坐标系 xOy 中,一直角三角形 ABC,∠C= 90°,B,C 在 x 轴上且关于原点 O 对称, D 在
边 BC 上, BD= 3DC,△ABC 的周长为 12. 若一双曲线 E 以 B,C 为焦点,且经过 A,D两点.
( 1 )求双曲线 E 的方程;
(2)若一过点 P m,0 m为非零常数 的直线与双曲线 E 相交于不同于双曲线顶点的两点 M ,N ,且
MP= λPN ,问在 x 轴上是否存在定点 G ,使 BC⊥ GM-λGN 若存在,求出所有这样定点 G 的
坐标;若不存在, 请说明理由.
62
梅花香自苦寒来
名校真题
18 (本小题满分 17分)
“学习强国”学习平台的答题竞赛包括三项活动,分别为“四人赛”“双人对战”和“挑战答题”. 在一天内参
与“四人赛”活动, 每局第一名积 3分, 第二、三名各积 2分, 第四名积 1分, 每局比赛相互独立. 在一天内
参与“双人对战”活动, 每局比赛有积分, 获胜者得 2 分, 失败者得 1 分, 每局比赛相互独立. 已知甲参加
“四人赛”活动, 每局比赛获得第一名、第二名的概率均为 1 ,获得第四名的概率为 1 ;甲参加“双人对
3 6
战”活动,
每局比赛获胜的概率为 3 .
4
(1)记甲在一天中参加“四人赛”和“双人对战”两项活动 (两项活动均只参加一局) 的总得分为 X ,求 X
的分布列与数学期望;
(2)“挑战答题”比赛规则如下:每位参赛者每次连续回答 5道题,在答对的情况下可以持续答题, 若第一
次答错时, 答题结束, 积分为 0分, 只有 5道题全部答对才可以获得 5个积分. 某市某部门为了吸引更多
职工参与答题,设置了一个“得积分进阶”活动,从 1 阶到 n n≥10 阶,规定每轮答题获得 5 个积分进
2 阶,没有获得积分进 1 阶, 按照获得的阶级给予相应的奖品, 记乙每次获得 5 个积分的概率互不影响,
均为 5 ,记乙进到 n阶的概率为 Pn ,求 P6 12 .
19 (本小题满分 17分)
已知函数 f x = ekx- lnx,k∈R .
(1)已知 k≥ 1 ,若 x≥ 1时, f x ≥ t恒成立,求 t的取值范围;
(2)当 k= 1时,求证: f x ≥ 1+a + 1-a lna .
63
宝剑锋从磨砺出
名校真题
名校经典真题汇编 (十一)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 命题“ x∈R,x2- 2x+ 4≤ 0”的否定为 ( )
A. x∈R,x2- 2x+ 4≥ 4 B. x∈R,x2- 2x+ 4≤ 4
C. x∈R,x2- 2x+ 4> 0 D. x R,x2- 2x+ 4> 0
z
2 已知复数 z1 与 z= 3- 2i在复平面内对应的点关于实轴对称,则 1+ = ( )1 i
-1-i 1-i -5-i 5-i
A. B. C. D.
2 2 2 2
3 如图所示,动点P在边长为 1的正方形ABCD的边上沿A→B→C→D运动,x表示动点P由A
点出发所经过的路程,y表示△APD的面积,则函数 y= f x 的大致图像是 ( ).
A. B.
C. D.
4 已知 a = 1, b = 3 ,a+ b= 3,1 ,则 a+ b与 a- b的夹角为 ( )
A. 60° B. 120° C. 45° D. 135°
64
梅花香自苦寒来
名校真题
5 a-x 2+x 6 的展开式中 x5 的系数是 12,则实数 a的值为 ( )
A. 4 B. 5 C. 6 D. 7
6 已知三棱台 ABC-A1B1C1 中,三棱锥 A-A1B1C1 的体积为 4,三棱锥 A1=ABC 的体积为 8,
则该三棱台的体积为 ( )
A. 12+ 3 3 B. 12+ 4 2 C. 12+ 4 3 D. 12+ 4 7
已知函数 f x = 3sin2 ωx + 17 sinωx- 3 ω>0 ,若 f x 在 π , 3π 上无零点,则 ω的2 2 2 2 2
取值范围是 ( )
2 8 2 2 8
A. 0, ∪ ,+∞9 9 B. 0, 9 ∪ , 3 9
0, 2C. 8 2 8 ∪ ,1 D. , ∪ [1, +∞)9 9 9 9
= 1 , = sin
1
8 设 a b e 8 - 1,c= ln 9 ,e为自然对数的底数,则 ( )
4 7
A. a> b> c B. a> c> b C. c> a> b D. b> c> a
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 在正方体 ABCD-A1B1C1D1 中,下列几种说法正确的有 ( )
A. AB,A1C 为异面直线 B. DB1⊥AD1
C. DC1 与平面 DBB1D1 所成的角为 45° D. 二面角 B1-AC-B 的正切值为 2
2 y2
10 已知双曲线 C: x - = 1 a>b>0 的左,右顶点分别为 A1,A2 ,点 P ,
a2 b2
Q是双曲线 C 上关于原点对称的两点 (异于顶点),直线 PA1,PA2 ,
QA 31 的斜率分别为 kPA ,k ,k ,若 k k1 PA2 QA1 PA1 PA = ,则下列说法正确的是 ( )2 4
A. 双曲线 C 的渐近线方程为 y=± 3 x
4
7
B. 双曲线 C 的离心率为
2
65
宝剑锋从磨砺出
名校真题
C. kPA k 为定值1 QA1
D tan ∠ A1PA2的取值范围为(0,+∞
11 定义在 R上的函数 f x 与 g x 的导函数分别为 f x 和 g x ,若 g x+1 - f 2-x = 2,
f x = g x-1 ,且 g x+2 为奇函数,则下 ( )
列说法一定正确的是
A. g 2 = 0 B. 函数 f x 关于 x= 2对称
2023
C. 函数 f x 是周期函数 D. g k = 0
k=1
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 在甲,乙,丙三个地区爆发了流感,这三个地区分别有 8%,6%,4%的人患了流感. 若这三个地区
的人数比为 5:3:2 ,现从这三个地区中任意选取一个人,这个人患流感的概率是 .
13 平面直角坐标系 xOy中,已知 AB 是圆 C: x-1 2 + y-1 2 = 2的一条弦,且 AC⊥BC,M 是
AB 的中点,当弦 AB 在圆 C 上运动时,直线 l : 3x- 4y- 9= 0上总存在 P,Q两点,使得 ∠PMQ≥ π
2
恒成立,则线段 PQ长度的取值范围是 .
14 “ 0,1数列”是每一项均为 0或 1的数列,在通信技术中应用广泛. 设 A是一个“ 0,1数列”,定
义数列 f A :数列 A中每个 0都变为“ 1,0,1”, A中每个 1都变为“ 0,1,0”, 所得到的新数列. 例如数
列 A:1,0 ,则数列 f A :0,1,0,1,0,1 . 已知数列 A1:1,0,1,0,1 ,且数列 Ak+1= f Ak , k= 1,2,3, ,记数
列 Ak 的所有项之和为 Sk ,则 Sk+Sk+1= .
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演算步骤。)
15 本小题满分 13分)
已知锐角 △ABC 的内角 A,B,C 的对边分别为 a,b,c ,且 2sinC- sinB = tanAcosB .
(1)求 A;
(2)若 a= 2 ,求 2c- b的取值范围.
66
梅花香自苦寒来
名校真题
16 (本小题满分 15分)
如图,在多面体 ABCDEF 中,梯形 ADEF 与平行四边形 ABCD 所在平面互相垂直, AF DE,DE⊥
AD,AD⊥BE,AF=AD= 1 DE= 1 , AB= 2 .
2
( 1 )求证: BF 平面 CDE ;
(2)判断线段 BE 上是否存在点 Q , ⊥ , BQ使得平面 CDQ 平面 BEF ?若存在 求出 的值;若不存在,
BE
说明理由.
17 (本小题满分 15分)
67
宝剑锋从磨砺出
名校真题
某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛, 竞赛奖励规则如
下, 得分在 [70,80)内的学生获三等奖, 得分在 [80,90)内的学生获二等奖,得分在 90,100 内的学生获
一等奖, 其他学生不得奖. 为了解学生对相关知识的掌握情况, 随机抽取 100 名学生的竞赛成绩, 并以此
为样本绘制了样本频率分布直方图, 如图所示.
(1)现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若该市所有参赛学生的成绩 X 近似服从正态分布 N μ,σ2 ,其中 σ≈ 15,μ 为样本平均数的估计值,
利用所得正态分布模型解决以下问题:
(i)若该市共有 10000 名学生参加了竞赛,试估计参赛学生中成绩超过 79 分的学生数 (结果四舍五入到
整数);
(ii)若从所有参赛学生中 (参赛学生数大于 10000 )随机抽取 3 名学生进行访谈,设其中竞赛成绩在 64
分以上的学生数为 ξ ,求随机变量 ξ的分布列和均值.
附参考数据:若随机变量 X 服从正态分布 N μ,σ2 ,
则 P μ-σ≤X≤μ+σ ≈ 0.6827,P μ-2σ≤X≤μ+2σ ≈ 0.9545 ,P μ-3σ≤X≤μ+3σ ≈ 0.9973.
18 (本小题满分 17分)
已知椭圆具有如下光学性质:从椭圆的一个焦点发出的光线射向椭圆上任一点,经椭圆反射后必经过另
x2 y2一个焦点. 若从椭圆 T: + = 1 a>b>02 的左焦点 F1 发出的光线,经过两次反射之后回到点 F1 ,a2 b
光线经过的路程为 8,椭圆 T 的离心率为 3 .
2
( 1 )求椭圆 T 的标准方程;
(2)设 D xD,0 ,且 xD> a ,过点 D 的直线 l 与椭圆 T 交于不同的两点 M ,N ,点 F2 是椭圆 T 的右焦
点,且 ∠DF2M 与 ∠DF2N 互补,求 △MNF2 面积的最大值.
68
梅花香自苦寒来
名校真题
19 (本小题满分 17分)
已知函数 f x = ln x+a - x2- x在 x= 0处取得极值.
(1)求实数 a的值;
(2)若关于 x的方程 f x =- 5 x+ b在区间 0,2 上恰有两个不同的实数根,求实数 b的取值范围;
2
(3)证明:对任意的正整数 n ,不等式 2+ 3 + 4 + + n+1 > ln n+1 都成立.
4 9 n2
69
宝剑锋从磨砺出
名校真题
名校经典真题汇编 (十二)
一、单项选择题 (本题共 8小题, 每小题 5分, 共 40分. 在每小题给出的四 个选项中, 只有一
项是符合题目要求的. )
1 若复数 2+ai 1+ i 的实部和虚部相等,则实数 a的值为 ( )
A. - 1 B. 0 C. 1 D. 2
2 已知集合 A= x,y ∣x2+y2≤2,x∈Z,y∈Z ,B= x,y ∣x+1>0 , 则 A∩B 的元素个数为
( )
A. 9 B. 8 C. 6 D. 5
3 已知向量 a= k,3 ,b= 1,4 ,c= 2,1 ,且 2a-3b ⊥ c ,则实数 k= ( )
- 9 0 3 15A. B. C. D.
2 2
4 设 m、n是空间两条不同直线, α、β是空间两个不同平面,则下列选项中错误的是 ( )
A. 当 n⊥ α时,“ n⊥ β”是“ α β”的充要条件
B. 当 m α时,“ m⊥ β”是“ α⊥ β”的充分不必要条件
C. 当 m α时,“ n α”是“ m n”的必要不充分条件
D. 当 m α时,“ n⊥ α”是“ m⊥n”的充分不必要条件
5 如图, 用 4种不同的颜色, 对四边形中的四个区域进行着色, 要求有公共边的两个区域不能用同
一种颜色, 则不同的着色方法有 ( )
A. 72 B. 56 C. 48 D. 36
70
梅花香自苦寒来
名校真题
6 若 sinα= 2sinβ,sin α+β tan α-β = 1 ,则 tanαtanβ= ( )
A. 2 3 1B. C. 1 D.
2 2
x
7 若函数 f x = e - a
x3
3 +lnx 只有一个极值点,则 a的取值范围是 ( )x
2 3 2 3
A. -∞, e B. (-∞,0] C. (-∞,0]∪ e e e4 9 D. -∞, ∪ 4 9
8 2021年 3月 30日,小米正式开始启用具备“超椭圆”数学之美的新 logo (如图所示),设计师的灵
n y n
感来源于曲线 C: x + = 1 n>0,n∈R . 当 n= 4,a= 2,b= 1时,下列关于曲线 C 的判断错误的a b
是 ( )
A. 曲线 C 关于 x轴和 y轴对称
B. 曲线 C 所围成的封闭图形的面积小于 8
C. 设 M 3,0 ,直线 x- y+ 3= 0交曲线 C 于 P、Q两点,则 △PQM 的周长小于 8
1
D. 曲线 C 上的点到原点 O的距离的最大值为 17 4
二、多项选择题 (本题共 3小题, 每小题 6分, 共 18分. 在每小题给出的选 项中, 有多项符合
题目要求. 全部选对的得 6分, 部分选对的得部分分, 有选错的得 0分.)
9 下列命题中, 真命题有 ( )
A. 数据 6,2,3,4,5,7,8,9,1,10的 70%分位数是 8.5
B. 若随机变量 X B 6, 1 ,则 D X 4 =3 9
C. 若事件 A,B 满足 0
D. 若随机变量 X N 2,σ2 ,P X>1 = 0.68 ,则 P 2≤x<3 = 0.18
10 若 a,b,c都是正数,且 2a= 3b= 6c 则 ( )
1 1
A. + = 2 1 1 1B. + = C. a+ b> 4c D. ab> 4c2
a b c a b c
71
宝剑锋从磨砺出
名校真题
11 对于定义在区间 D上的函数 f x ,若满足: x1,x2∈D且 x1< x2 ,都有 f x1 ≤ f x2 ,则称
函数 f x 为区间 D上的“非减函数”,若 f x 为区间 0,2 上的“非减函数”,且 f 2 = 2,f x +
f 3 2-x = 2 ,又当 x∈ ,2
时, f x ≤ 2 x-1 恒成立,下列命题中正确的有 ( )2
A. f 1 = 1 B. x ∈ 3 0 ,2 ,f x0 < 12
f 1 + f 2 + f 25C. + f 7 = 4 1D. x∈ 0, ,f f x ≤-f x + 24 3 18 4 2
三、填空题 (本题共 3小题, 每小题 5分, 共 15分. )
12 已知点 P为抛物线 C:y2= 4x上的一个动点,直线 l:x=-1 ,点 Q为圆 M : x+3 2 + y-3 2 = 1
上的动点,则点 P到直线 l的距离与 PQ 之和的最小值为 .
13 已知三棱锥 P-ABC 满足 PA= 1,PA⊥平面 ABC,AC⊥BC ,若 V 2P-ABC= ,则其外接球3
体积的最小值为 .
14 已知 f x = ex ( e为自然对数的底数), g x = lnx+ 2 ,直线 l是 f x . 与 g x 的公切线,则
直线 l的方程为 .
四、解答题 (本题共 5小题, 共 77分. 解答应写出文字说明、证明过程或演 算步骤.)
15 (本小题满分 13分)
已知数列 an 的首项为正数,其前 n 项和 Sn 满足 2Sn= 3an- 8- . (1)求实数 λ 的值,使得4Sn 3an
S2n+λ 是等比数列;
n
(2)设 bn= 3 ,求数列 b2n 的前 n项和.SnSn+1
72
梅花香自苦寒来
名校真题
16 (本小题满分 15分)
如图,四棱锥 P-ABCD的底面 ABCD是边长为 2的正方形, PA= PB= 2 .
(1)证明: ∠PAD=∠PBC ;
(2)当直线 PA与平面 PCD所成角的正弦值最大时,求此时二面角 P-AB-C 的大小.
17 (本小题满分 15分)
某数学兴趣小组为研究本校学生数学成绩与语文成绩的关系, 采取有放回的简单随机抽样, 从学校抽取
样本容量为 200的样本, 将所得数学成绩与语文成绩的样本观测数据整理如下:
数学成绩 语文成绩 合计
优秀 不优秀
优秀 50 30 80
不优秀 40 80 120
合计 90 110 200
(1)根据 α= 0.010的独立性检验,能否认为数学成绩与语文成绩有关联
P B∣A
(2)在人工智能中常用 L B∣
A = 表示在事件 A发生的条件下事件 B 发生的优势,在统计中
P B∣A
称为似然比. 现从该校学生中任选一人, A表示“选到的学生语文成绩不优秀”, B 表示“选到的学生数学
成绩不优秀”,请利用样本数据,估计 L B∣A 的值;
(3)现从数学成绩优秀的样本中,按分层抽样的方法选出 8 人组成一个小组, 从抽取的 8 人里再随机抽
取 3人参加数学竞赛, 求这 3人中, 语文成绩优秀的人数 X 的概率分布列及数学期望.
73
宝剑锋从磨砺出
名校真题
附: χ2= α 0.050 0.010 0.001
n ad-bc 2
x 3.841 6.635 10.828
a+b c+d a+c α b+d
18 (本小题满分 17分)
已知双曲线 E 的顶点为 A -1,0 ,B 1,0 ,过右焦点 F 作其中一条渐近线的平行线,与另一条渐近线交
于点 G ,且 S 3 2△OFG= (O 为坐标原点). 点 P 为 x 轴正半轴上异于点 B 的任意点,过点 P 的直线 l4
交双曲线于 C,D两点,直线 AC 与直线 BD交于点 H .
(1)求双曲线 E 的标准方程;
(2)求证: OP OH 为定值.
19 (本小题满分 17分)
已知函数 f x = ln x+1 + sinx+ cosx .
(1)当 x∈ 0,π 时,求证: f x > 0;
(2)若 f x ≤ ax+ 1对 x>-1恒成立,求 a .
74
梅花香自苦寒来
名校真题
2025届新高考数学名校真题经典必刷卷
数学参考答案 (-)
一、单项选择题
题号 1 2 3 4 5 6 7 8
答案 C B C A B C C A
1. C【解析】由已知集合M={x ∣ 2x+ 1< 3}= {x ∣ x< 1} ,因为M∩N=N ,所以 N M ,所以 a≤ 1 .
故选 C .
2. B【解析】因为 x+ i 3+yi = 3x-y + 3+xy i= 2+ 4i . 所以 3x- y= 2,3+ xy= 4 ,故 xy= 1 ,故
选 B.
3. 2 2C【解析】点 A,B,C 不共线,若 “ AB与 AC 的夹角为锐角”,则 AB AC> 0, AB+AC = AB-AC
+ 4AB 2 2AC = BC + 4AB AC> BC , ∴ " AB与 AC 的夹角为锐角 " " AB+AC > BC ";若
2
AB+AC > BC ,则 |AB+ AC 2> AC-AB ,化简得 AB AC> 0 ,而点 A,B,C 不共线,故 AB
与 AC 的夹角为锐角, ∴ “ AB+AC > BC ” " AB与 AC 的夹角为锐角 ",故选 C .
x
4. A【解析】∵ f x = 2 -1 sinx ,定义域为 R, ∴ f 2 2e -x = -1 sin -x =- -11+ex 1+e-x 1+ex
sinx= 2 -1 sinx= f x , ∴函数 f x 为偶函数,故排除 C,D ,当 x= 2时, f 2 = 2 -11+ex 1+e2
sin2< 0 ,故排除 B, 故选 A.
5. B【解析】如图所示,由题知 ∠BAD=∠BCD= 90°,AD= 2,CD= 4 ,
∴AC BD= AD+DC BD
=AD BD+DC BD
= AD BD cos∠BDA- DC BD cos∠BDC
2 = 2 AD - DC = 4- 16=-12 .
故选 B.
6. C【解析】因为底面 ABC 是边长为 2 3 的正三角形,M 为 AC 的中点,所以 BM⊥AM ,BM= 3 . 以
BM ,AM ,AP为长方体的长,宽,高构造长方体 AMBE-PNGF ,如下图所示,
1
宝剑锋从磨砺出
名校真题
所以长方体 AMBE-PNGF 的外接球即为三棱锥 P-ABM 的外接球,
因为 PB为长方体 AMBE-PNGF 的体对角线,所以球心 O为 PB中点,外接球半径 R= 1 PB .
2
因为正三角形 ABC 边长为 2 3 ,PA= 2,PA⊥底面 ABC,AB 平面 ABC ,
所以 PA⊥AB,PB= 2 3 2 +22= 4 ,所以 R= 2 ,
因为 D是球 O上一点,要使三棱锥 D-PAC 的体积最大,
则点 D到平面 PAC 的距离最大为球的半径 R与球心 O到平面 PAC 距离 d之和,
因为由题可知,球 O与平面 PAC 的截面为长方体 AMBE-PNGF 的一侧面 AMNP ,
设矩形 AMNP的中心即 PM 中点为 O ,所以 d= OO = 1 BM = 3 ,
2 2
所以点 D到平面 PAC 的距离的最大值为 R+ d= 2+ 3 = 7 ,
2 2
故三棱锥 D-PAC 的体积的最大值是V = 1 × 1D-PAC × 2× 2 3 ×
7 = 7 3 .
3 2 2 3
故选 C .
7. C【解析】方程m x2+y2+2y+1 = x-2y+3 2 ,m> 0 , 即为m x2+ y+1 2 = x-2y+3 2 ,可得
x2+ y+1 2
m x2+ y+1 2 = x-2y+3 , 则 = 5 ,可得动点 P x,y 到定点 (0, - 1)和定直线
x-2y+1 m
x- 2y+ 3= 0的距离的比为常数 5 ,由双曲线的定义,可得 5 > 1 ,解得 0
C .
8. A【解析】由题意知: 13π + π = T + kT 或 13π + π = 3T + kT,k∈ Z ,
12 6 4 12 6 4
∴ 5π = 1 +k 2π 或 5π = 3 +k 2π ,4 4 ω 4 4 ω
∴ω= 2 1+4k 或 ω= 2 3+4k ,k∈ Z ,
5 5
∵ f x 13π 19π 在 , 上单调递减, ∴
19π - 13π ≤ T , ∴ π ≤ 1 2π ω≤ 2 ,
12 12 12 12 2 2 2 ω
① 当 ω= 2 1+4k ,k∈ Z 时. 取 k= 0时, ω= 2 ,此时 f x = sin 2 x+ π ,5 5 5 15
当 x∈ 13π , 19π
2
时, x+
π ∈ π , 7π ,满足 f x 在 13π 19π 2
12 12 5 15 2 10
, 上单调递减, ∴ω= 符合;12 12 5
取 k= 1时, ω= 2 ,此时 f x = sin 2x+ π ,3
当 x∈ 13π , 19π π 5π 7π 时, 2x+ ∈ , ,满足 f x 在
13π
,
