《培优卷》——第二单元多边形的面积(含解析)-2025-2026学年五年级上册数学(苏教版)
文档属性
| 名称 | 《培优卷》——第二单元多边形的面积(含解析)-2025-2026学年五年级上册数学(苏教版) |  | |
| 格式 | docx | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 14:49:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《培优卷》——第二单元多边形的面积(单元测试)-2025-2026学年五年级上册数学(苏教版)
一、单选题
1. 用木条钉成的长方形拉成一个平行四边形,它的高和面积( )。
A.不变 B.都比原来大 C.都比原来小
2.平行四边形和三角形的面积相等,已知三角形的高是平行四边形高的3倍,三角形的底是28cm,平行四边形的底是( )cm。
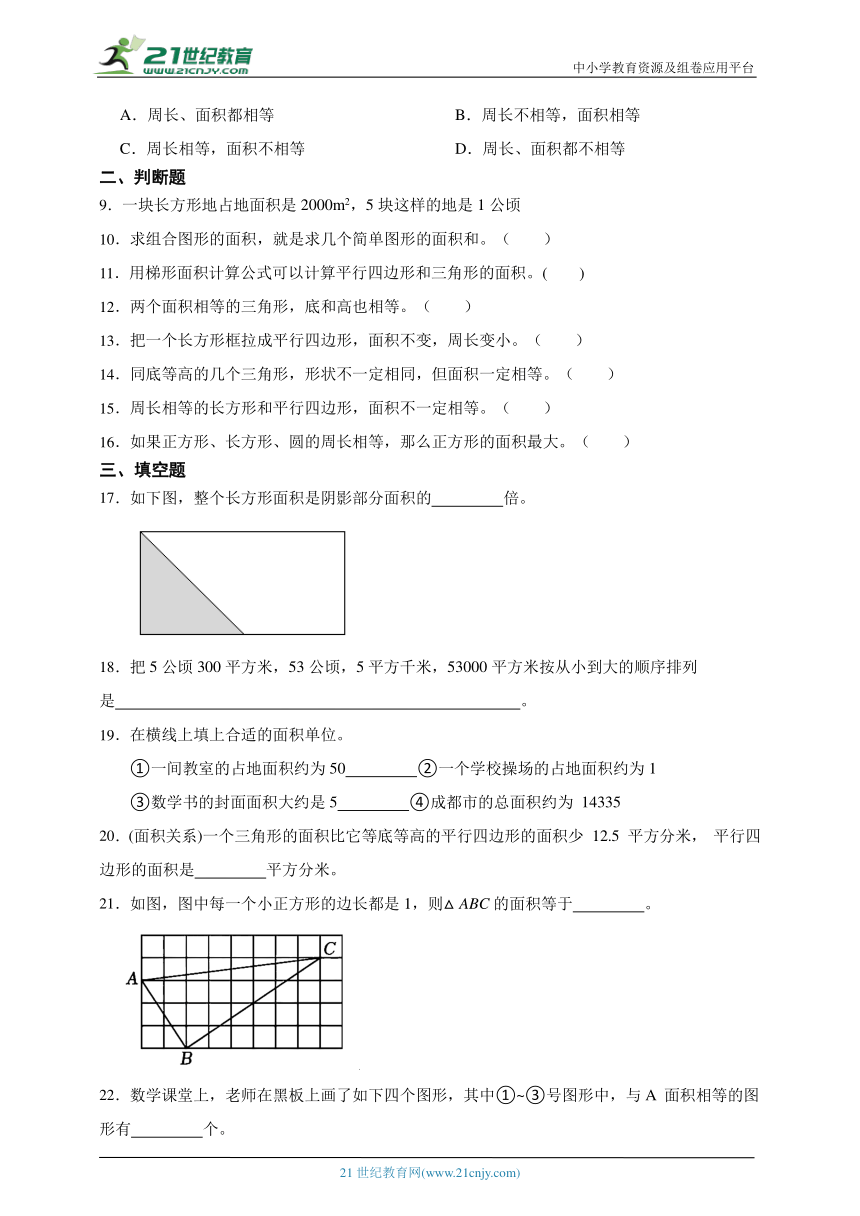
A.42 B.56 C.84
3.一个三角形和一个平行四边形底相等,面积也相等。平行四边形的高是16cm,三角形的高是( )cm。
A.8 B.16 C.32 D.64
4.如果一块草地的面积是1公顷,那么1平方千米的土地相当于( )块这样的草地。
A.100 B.1000 C.10000 D.100000
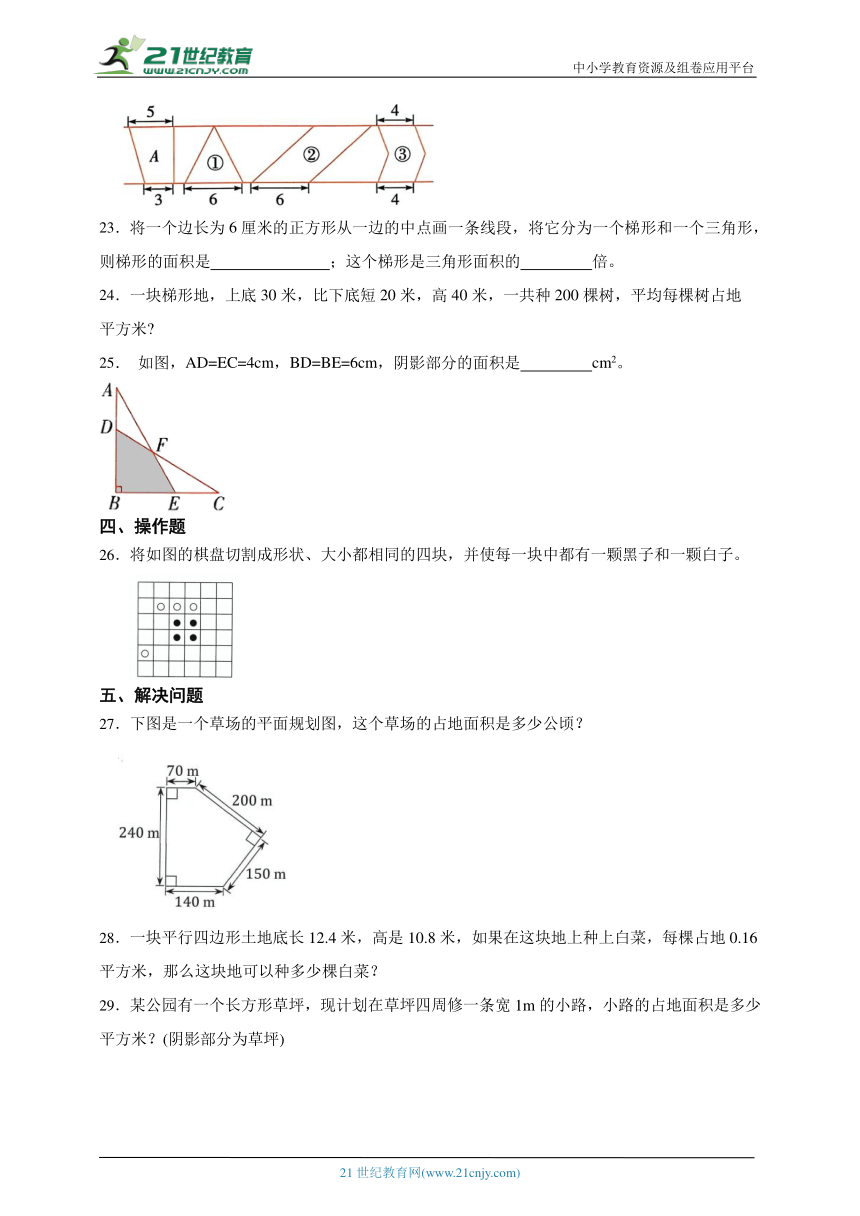
5.一个果园种了5000棵果树,平均每棵果树占地4平方米,这个果园占地( )公顷。
A.200 B.20 C.2
6.王大伯用46米篱笆在河边围了一块梯形的地种菜(如图,河岸不要篱笆)。这块地的面积是( )平方米。
A.520 B.260 C.无法确定
7.有个平行四边形,它的两条邻边分别长5分米和7分米,如果其中一条边上的高是6分米,那么这个平行四边形的面积是( )平方分米.
A.30 B.25 C.42 D.无法判断
8.图中,长方形被分成了甲、乙两部分,这两部分( )。
A.周长、面积都相等 B.周长不相等,面积相等
C.周长相等,面积不相等 D.周长、面积都不相等
二、判断题
9.一块长方形地占地面积是2000m2,5块这样的地是1公顷
10.求组合图形的面积,就是求几个简单图形的面积和。( )
11.用梯形面积计算公式可以计算平行四边形和三角形的面积。( )
12.两个面积相等的三角形,底和高也相等。( )
13.把一个长方形框拉成平行四边形,面积不变,周长变小。( )
14.同底等高的几个三角形,形状不一定相同,但面积一定相等。( )
15.周长相等的长方形和平行四边形,面积不一定相等。( )
16.如果正方形、长方形、圆的周长相等,那么正方形的面积最大。( )
三、填空题
17.如下图,整个长方形面积是阴影部分面积的 倍。
18.把5公顷300平方米,53公顷,5平方千米,53000平方米按从小到大的顺序排列是 。
19.在横线上填上合适的面积单位。
①一间教室的占地面积约为50 ②一个学校操场的占地面积约为1
③数学书的封面面积大约是5 ④成都市的总面积约为 14335
20.(面积关系)一个三角形的面积比它等底等高的平行四边形的面积少 12.5 平方分米, 平行四边形的面积是 平方分米。
21.如图,图中每一个小正方形的边长都是1,则△ABC的面积等于 。
22.数学课堂上,老师在黑板上画了如下四个图形,其中①~③号图形中,与A 面积相等的图形有 个。
23.将一个边长为6厘米的正方形从一边的中点画一条线段,将它分为一个梯形和一个三角形,则梯形的面积是 ;这个梯形是三角形面积的 倍。
24.一块梯形地,上底30米,比下底短20米,高40米,一共种200棵树,平均每棵树占地 平方米
25. 如图,AD=EC=4cm,BD=BE=6cm,阴影部分的面积是 cm2。
四、操作题
26.将如图的棋盘切割成形状、大小都相同的四块,并使每一块中都有一颗黑子和一颗白子。
五、解决问题
27.下图是一个草场的平面规划图,这个草场的占地面积是多少公顷?
28.一块平行四边形土地底长12.4米,高是10.8米,如果在这块地上种上白菜,每棵占地0.16平方米,那么这块地可以种多少棵白菜?
29.某公园有一个长方形草坪,现计划在草坪四周修一条宽1m的小路,小路的占地面积是多少平方米?(阴影部分为草坪)
30.如图,小正方形的边长为8厘米,大正方形的边长为12厘米,阴影部分的面积是多少平方厘米?
31.小红锻炼身体,每天绕一个正方形广场走5圈,共走了20000米,这个广场的面积是多少平方千米?
32.塔克拉玛干沙漠是我国面积最大的沙漠,也是世界第二大流动沙漠。为了防风固沙,某志愿队要开垦3公顷的沙地植树造林。该志愿队现已经开垦出一块长250米、宽80米的长方形沙地,还要开垦多少公顷?
33.一个平行四边形, 它的底边减少6分米后还剩余18分米, 面积因此而减少72平方分米,这个平行四边形原来的面积是多少平方分米
34.李叔叔利用一面墙,如下图,用20米长的绳子,围成了一个直角梯形,这个梯形的高是6米,这个梯形的面积是多少平方米?
答案解析部分
1.【答案】C
【解析】【解答】解:用木条钉成的长方形拉成一个平行四边形,它的高和面积都比原来小。
故答案为:C。
【分析】把长方形木框拉成平行四边形后,周长不变;长方形的长和平行四边形的底相等,长方形的宽大于平行四边形的高,所以它的面积变小了。
2.【答案】A
【解析】【解答】解:平行四边形的高看做单位1,则三角形的高是3;
28×3÷2=42(平方厘米)
42÷1=42(厘米)
故答案为:A。
【分析】三角形面积=底×高÷2,三角形面积÷平行四边形的高=平行四边形的底。
3.【答案】C
【解析】【解答】解:16×2=32(cm)
故答案为:C。
【分析】因为 一个三角形和一个平行四边形底相等,面积也相等,平行四边形的高是16cm, 那么三角形的高必须是平行四边形高的2倍,所以三角形的高=平行四边形的高×2。
4.【答案】A
【解析】【解答】解:1平方千米=100公顷,
100÷1=100(块)。
故答案为:A。
【分析】1平方千米的土地相当于这样草地的块数=1平方千米÷平均每块这样草地的面积。
5.【答案】C
【解析】【解答】解:5000×4=20000(平方米)=2(公顷)。
故答案为:C。
【分析】果园种果树棵数×平均每棵果树占地平方数=这个果园占地面积;平方米÷10000=公顷,据此解答。
6.【答案】B
【解析】【解答】46-20=26(米)
26×20÷2
=520÷2
=260(平方米)
故答案为:B。
【分析】观察图可知,篱笆的长度-梯形的高=梯形的上底+下底;要求梯形的面积,应用公式:梯形的面积=(上底+下底)×高÷2,据此列式解答。
7.【答案】A
【解析】【解答】5×6=30(平方分米)。
故答案为:A。
【分析】一条边上的高是6分米,说明6分米只能是边为5分米上的高,平行四边形面积=底×高。
8.【答案】C
【解析】【解答】解:甲、乙两部分周长相等,面积不相等。
故答案为:C。
【分析】甲的周长=乙的周长=长方形的长+长方形的宽+中间曲线的长度;甲的面积<乙的面积。
9.【答案】正确
【解析】【解答】2000×5=10000(平方米)=1(公顷),原题说法正确.
故答案为:正确.
【分析】根据题意可知,用每块长方形地的面积×块数=总面积,依据1公顷=10000平方米,据此换算单位即可.
10.【答案】正确
【解析】【解答】解:求组合图形的面积,就是求几个简单图形的面积和,原题干说法正确。
故答案为:正确。
【分析】由几个简单的图形组合在一起就是组合图形,求组合图形的面积,就是求几个简单图形的面积和。
11.【答案】正确
【解析】【解答】解:用两个完全一样的梯形可以拼成平行四边形,这个平行四边形的面积=梯形的面积×2;
平行四边形又可以切成两个完全一样的三角形,所以用梯形面积计算公式可以计算平行四边形和三角形的面积。
故答案为:正确。
【分析】用两个完全一样的梯形可以拼成平行四边形,用两个完全一样的三角形可以拼成平行四边形,据此计算。
12.【答案】错误
【解析】【解答】解:两个面积相等的三角形,底和高不一定相等。
故答案为:错误。
【分析】三角形的面积=底×高÷2,三角形面积相等,底和高不一定相等。
13.【答案】错误
【解析】【解答】解:把一个长方形框拉成平行四边形,面积变小,周长不变。原题说法错误。
故答案为:错误。
【分析】把一个长方形框拉成平行四边形,四条边的长度是不变的,所以周长不变。长方形的宽比平行四边形的高长,所以平行四边形的面积就小于长方形的面积,面积是变小的。
14.【答案】正确
【解析】【解答】解:三角形的面积=底×高÷2,只要三角形的底与高相等,面积就相等。
故答案为:正确。
【分析】同底等高的三角形,面积相等。
15.【答案】正确
【解析】【解答】解:周长相等的长方形和平行四边形,面积不一定相等,说法正确。
故答案为:正确。
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,周长相等的长方形和平行四边形,可将长方形拉成一个平行四边形,即这个过程中高减小,长方形的面积大于平行四边形的面积,本题据此解答。
16.【答案】错误
【解析】【解答】解:假设长方形、正方形、圆,它们的周长为12.56厘米;
①长方形的长可以为3.13厘米,宽为3.15厘米,面积是:
3.13×3.15=9.8595(平方厘米);
②正方形的边长为3.14厘米,面积是:
3.14×3.14=9.8596(平方厘米);
③圆的面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
④三角形的底约4.19厘米,高约是3.62厘米
4.19×3.62÷2
=15.1678÷2
=7.5839(平方厘米)
12.56平方厘米>9.8596平方厘米>9.8595平方厘米>7.5839平方厘米。
故答案为:错误。
【分析】周长相等的长方形、正方形、圆、三角形,其中圆的面积最大。
17.【答案】4
【解析】【解答】解:4÷1=4。
故答案为:4。
【分析】把整个长方形平均分成了4份,阴影部分占1份,所以整个长方形面积是阴影部分面积的4倍。
18.【答案】5公顷300平方米<53000平方米<53公顷<5平方千米
【解析】【解答】解:5公顷300平方米=50000平方米+300平方米=50300平方米,
53公顷=530000平方米,
5平方千米=5000000平方米,
50300平方米<53000平方米<53公顷<5平方千米
即:5公顷300平方米<53000平方米<53公顷<5平方千米
故答案为:5公顷300平方米<53000平方米<53公顷<5平方千米。
【分析】1平方千米=1000000平方米;1平方千米=100公顷;1公顷=10000平方米;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
19.【答案】m2;公顷;dm2;km2
【解析】【解答】解:①一间教室的占地面积约为501平方米 ②一个学校操场的占地面积约为12公顷
③数学书的封面面积大约是53平方分米 ④成都市的总面积约为 14335平方千米
故答案为:平方米;公顷;平方分米;平方千米。
【分析】根据生活经验以及对面积单位和数据大小的认识,结合实际情况选择合适的单位即可。
20.【答案】25
【解析】【解答】解:
12.5×2=25(平方分米)
故答案为:25
【分析】根据三角形的面积=底×高÷2,平行四边形的面积=底×高,因为三角形和平行四边形等底等高,则三角形的面积是平行四边形的面积的一半,由此即可求出平行四边形的面积。
21.【答案】13
【解析】【解答】解:8×4-1×8÷2-2×3÷2-6×4÷2
=32-4-3-12
=13;
故答案为:13。
【分析】三角形ABC的面积等于长方形的面积减去三个直角三角形的面积,据此求解。
22.【答案】1
【解析】【解答】解:设A图形的高为h,根据图形所示,可得
A面积为:(3+5)×h÷2=4h
图①面积为:6×h÷2=3h
图②面积为:6×h=6h
图③面积为:4×h=4h
所以与图形A 面积相等的图形有1个。
故答案为:1
【分析】由图可知,这些图形的高相同,假设高为h,根据梯形、三角形、平行四边形面积公式,分别求出其面积,即可判断
23.【答案】27平方厘米;3
【解析】【解答】解:6÷2=3(厘米)
(3+6)×6÷2
=9×6÷2
=54÷2
=27(平方厘米)
3×6÷2
=18÷2
=9(平方厘米)
27÷9=3
故答案为:27平方厘米;3。
【分析】梯形的面积=(上底+下底)×高÷2;其中,上底=正方形的边长÷2,下底、高=正方形的边长;三角形的面积=底×高÷2;梯形是三角形面积的倍数=梯形的面积÷三角形的面积。
24.【答案】8
【解析】【解答】[30+(30+20)]×40÷2÷200=8(棵)
故答案为:8.
【分析】根据梯形面积计算公式求出梯形地的面积,再用梯形地的面积除以种树的棵数即可.
25.【答案】22.5
【解析】【解答】解:BD=(6÷4)×AD=1.5×AD,
6×(4+6)÷2=30(cm2),
①的面积=7.5 cm2,
阴影部分的面积=30-7.5=22.5(cm2)。
故答案为:22.5。
【分析】如图,连接BF、BF:
根据题意可知,图形关于直线BF对称,所以②的面积=③的面积,①的面积=④的面积,因为图①和图②等高,可以求出BD与AD的关系,可以得到②的面积=③的面积=1.5×①的面积, ②的面积+①的面积+③的面积=(1.5×2+1)×①的面积,据此先求出①的面积,再求出阴影部分的面积。
26.【答案】解:如图:
首先在相同颜色的棋子之间划出切分线,以中心点为旋转中心,旋转90°、180°、270°之后,得到一些新的切分线,同时考虑到每块包含一颗黑子和一颗白子的要求,以及每一块的面积应该是36÷4=9,即含有9个小正方格,先找到符合要求的一块后,让它绕中心旋转90°、180°、270°,便得到其他三块。
【解析】【分析】因为每一块中都要带有白子、黑子各一个.根据黑子的位置特点,先把四个黑子划分出四个部分,再根据白子的位置特点将中图形划分出四个完全相同的四个图形即可.
27.【答案】解:(70+140)×240÷2 =25200(m2)
150×200÷2=15000(m2)
25200+15000=40200(m2)
40200m2=4.02公顷
答:这个草场的占地面积是4.02公顷。
【解析】【分析】如图,,草场的占地面积=梯形面积+三角形面积,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,据此解答。
28.【答案】解:12.4×10.8÷0.16=133.92÷0.16=837(棵)答:这块地可以种白菜837棵.
【解析】【分析】根据“平行四边形面积=底×高”列式求出土地的面积,然后用土地面积除以每棵的占地面积即可求出种菜的棵数.
29.【答案】解:23×18-(23-1-1)×(18-1-1)
=414-336
=78(m2)
答:小路的占地面积是78平方米。
【解析】【分析】小路的面积=大长方形面积-小长方形面积,长方形的面积=长×宽,据此解答。
30.【答案】解:
如图,设AB的长为x厘米
8x÷2+(x+12)×12÷2=12×(8+12)÷2
4x+6x+72=12×20÷2
10x=120-72
10x=48
x=4.8
4.8×12÷2
=4.8×6
=28.8(平方厘米)
答:阴影部分的面积是28.8平方厘米。
【解析】【分析】如图:阴影部分的面积是底为AB,高为12cm的三角形的面积;设AB的长为厘米;根据三角形ABC面积+梯形ABED面积=三角形CDE的面积,列出方程,求出AB的长,然后再根据三角形的面积公式进行解答。
31.【答案】解:20000÷5÷4=1000(米)
1000米=1千米
1×1=1(平方千米)
答:这个广场的面积是1平方千米。
【解析】【分析】用共走的长度除以5求出每圈的长度,用每圈的长度除以4求出边长,把边长换算成千米,再用边长乘边长求出面积即可。
32.【答案】1公顷
33.【答案】解:18+6=24(分米)
72÷6=12(分米)
24×12=288(平方分米)
答:这个平行四边形原来的面积是288平方分米。
【解析】【分析】平行四边形的底=底边减少的长度+底边还剩的长度,平行四边形的底边减少了,高不变,面积也减少了,那么平行四边形的高=平行四边形减少了的面积÷平行四边形的底边减少的长度;平行四边形的面积=底×高。
34.【答案】解:20-6=14(米)
14×6÷2
=84÷2
=42(平方米)
答:这个梯形的面积是42平方米。
【解析】【分析】这个梯形的面积=上、下底的和×高÷2;其中,上、下底的和=绳子的长-梯形的高。
试题分析部分
1、试卷总体分布分析
总分:103分
分值分布 客观题(占比) 48.0(46.6%)
主观题(占比) 55.0(53.4%)
题量分布 客观题(占比) 23(67.6%)
主观题(占比) 11(32.4%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 9(26.5%) 26.0(25.2%)
解决问题 8(23.5%) 40.0(38.8%)
操作题 1(2.9%) 5.0(4.9%)
单选题 8(23.5%) 16.0(15.5%)
判断题 8(23.5%) 16.0(15.5%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (47.1%)
2 容易 (26.5%)
3 困难 (26.5%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 公顷、平方千米与平方米之间的换算与比较 13.0(12.6%) 4,5,9,18,32
2 三角形的面积 30.0(29.1%) 2,3,8,11,12,14,17,20,21,22,27,30
3 三位数乘两位数的笔算乘法 5.0(4.9%) 32
4 平面图形的切拼 5.0(4.9%) 26
5 长方形的面积 20.0(19.4%) 9,13,15,16,17,29,32
6 平方厘米、平方分米、平方米的认识与使用 8.0(7.8%) 19
7 梯形的面积 24.0(23.3%) 6,11,16,22,23,24,27,34
8 长方形的周长 4.0(3.9%) 13,15
9 公顷和平方千米的认识与使用 13.0(12.6%) 19,31
10 组合图形面积的巧算 23.0(22.3%) 10,21,22,25,26,27,29
11 平行四边形的面积 26.0(25.2%) 1,2,7,11,13,15,20,22,28,33
12 正方形的面积 12.0(11.7%) 16,26,31
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《培优卷》——第二单元多边形的面积(单元测试)-2025-2026学年五年级上册数学(苏教版)
一、单选题
1. 用木条钉成的长方形拉成一个平行四边形,它的高和面积( )。
A.不变 B.都比原来大 C.都比原来小
2.平行四边形和三角形的面积相等,已知三角形的高是平行四边形高的3倍,三角形的底是28cm,平行四边形的底是( )cm。
A.42 B.56 C.84
3.一个三角形和一个平行四边形底相等,面积也相等。平行四边形的高是16cm,三角形的高是( )cm。
A.8 B.16 C.32 D.64
4.如果一块草地的面积是1公顷,那么1平方千米的土地相当于( )块这样的草地。
A.100 B.1000 C.10000 D.100000
5.一个果园种了5000棵果树,平均每棵果树占地4平方米,这个果园占地( )公顷。
A.200 B.20 C.2
6.王大伯用46米篱笆在河边围了一块梯形的地种菜(如图,河岸不要篱笆)。这块地的面积是( )平方米。
A.520 B.260 C.无法确定
7.有个平行四边形,它的两条邻边分别长5分米和7分米,如果其中一条边上的高是6分米,那么这个平行四边形的面积是( )平方分米.
A.30 B.25 C.42 D.无法判断
8.图中,长方形被分成了甲、乙两部分,这两部分( )。
A.周长、面积都相等 B.周长不相等,面积相等
C.周长相等,面积不相等 D.周长、面积都不相等
二、判断题
9.一块长方形地占地面积是2000m2,5块这样的地是1公顷
10.求组合图形的面积,就是求几个简单图形的面积和。( )
11.用梯形面积计算公式可以计算平行四边形和三角形的面积。( )
12.两个面积相等的三角形,底和高也相等。( )
13.把一个长方形框拉成平行四边形,面积不变,周长变小。( )
14.同底等高的几个三角形,形状不一定相同,但面积一定相等。( )
15.周长相等的长方形和平行四边形,面积不一定相等。( )
16.如果正方形、长方形、圆的周长相等,那么正方形的面积最大。( )
三、填空题
17.如下图,整个长方形面积是阴影部分面积的 倍。
18.把5公顷300平方米,53公顷,5平方千米,53000平方米按从小到大的顺序排列是 。
19.在横线上填上合适的面积单位。
①一间教室的占地面积约为50 ②一个学校操场的占地面积约为1
③数学书的封面面积大约是5 ④成都市的总面积约为 14335
20.(面积关系)一个三角形的面积比它等底等高的平行四边形的面积少 12.5 平方分米, 平行四边形的面积是 平方分米。
21.如图,图中每一个小正方形的边长都是1,则△ABC的面积等于 。
22.数学课堂上,老师在黑板上画了如下四个图形,其中①~③号图形中,与A 面积相等的图形有 个。
23.将一个边长为6厘米的正方形从一边的中点画一条线段,将它分为一个梯形和一个三角形,则梯形的面积是 ;这个梯形是三角形面积的 倍。
24.一块梯形地,上底30米,比下底短20米,高40米,一共种200棵树,平均每棵树占地 平方米
25. 如图,AD=EC=4cm,BD=BE=6cm,阴影部分的面积是 cm2。
四、操作题
26.将如图的棋盘切割成形状、大小都相同的四块,并使每一块中都有一颗黑子和一颗白子。
五、解决问题
27.下图是一个草场的平面规划图,这个草场的占地面积是多少公顷?
28.一块平行四边形土地底长12.4米,高是10.8米,如果在这块地上种上白菜,每棵占地0.16平方米,那么这块地可以种多少棵白菜?
29.某公园有一个长方形草坪,现计划在草坪四周修一条宽1m的小路,小路的占地面积是多少平方米?(阴影部分为草坪)
30.如图,小正方形的边长为8厘米,大正方形的边长为12厘米,阴影部分的面积是多少平方厘米?
31.小红锻炼身体,每天绕一个正方形广场走5圈,共走了20000米,这个广场的面积是多少平方千米?
32.塔克拉玛干沙漠是我国面积最大的沙漠,也是世界第二大流动沙漠。为了防风固沙,某志愿队要开垦3公顷的沙地植树造林。该志愿队现已经开垦出一块长250米、宽80米的长方形沙地,还要开垦多少公顷?
33.一个平行四边形, 它的底边减少6分米后还剩余18分米, 面积因此而减少72平方分米,这个平行四边形原来的面积是多少平方分米
34.李叔叔利用一面墙,如下图,用20米长的绳子,围成了一个直角梯形,这个梯形的高是6米,这个梯形的面积是多少平方米?
答案解析部分
1.【答案】C
【解析】【解答】解:用木条钉成的长方形拉成一个平行四边形,它的高和面积都比原来小。
故答案为:C。
【分析】把长方形木框拉成平行四边形后,周长不变;长方形的长和平行四边形的底相等,长方形的宽大于平行四边形的高,所以它的面积变小了。
2.【答案】A
【解析】【解答】解:平行四边形的高看做单位1,则三角形的高是3;
28×3÷2=42(平方厘米)
42÷1=42(厘米)
故答案为:A。
【分析】三角形面积=底×高÷2,三角形面积÷平行四边形的高=平行四边形的底。
3.【答案】C
【解析】【解答】解:16×2=32(cm)
故答案为:C。
【分析】因为 一个三角形和一个平行四边形底相等,面积也相等,平行四边形的高是16cm, 那么三角形的高必须是平行四边形高的2倍,所以三角形的高=平行四边形的高×2。
4.【答案】A
【解析】【解答】解:1平方千米=100公顷,
100÷1=100(块)。
故答案为:A。
【分析】1平方千米的土地相当于这样草地的块数=1平方千米÷平均每块这样草地的面积。
5.【答案】C
【解析】【解答】解:5000×4=20000(平方米)=2(公顷)。
故答案为:C。
【分析】果园种果树棵数×平均每棵果树占地平方数=这个果园占地面积;平方米÷10000=公顷,据此解答。
6.【答案】B
【解析】【解答】46-20=26(米)
26×20÷2
=520÷2
=260(平方米)
故答案为:B。
【分析】观察图可知,篱笆的长度-梯形的高=梯形的上底+下底;要求梯形的面积,应用公式:梯形的面积=(上底+下底)×高÷2,据此列式解答。
7.【答案】A
【解析】【解答】5×6=30(平方分米)。
故答案为:A。
【分析】一条边上的高是6分米,说明6分米只能是边为5分米上的高,平行四边形面积=底×高。
8.【答案】C
【解析】【解答】解:甲、乙两部分周长相等,面积不相等。
故答案为:C。
【分析】甲的周长=乙的周长=长方形的长+长方形的宽+中间曲线的长度;甲的面积<乙的面积。
9.【答案】正确
【解析】【解答】2000×5=10000(平方米)=1(公顷),原题说法正确.
故答案为:正确.
【分析】根据题意可知,用每块长方形地的面积×块数=总面积,依据1公顷=10000平方米,据此换算单位即可.
10.【答案】正确
【解析】【解答】解:求组合图形的面积,就是求几个简单图形的面积和,原题干说法正确。
故答案为:正确。
【分析】由几个简单的图形组合在一起就是组合图形,求组合图形的面积,就是求几个简单图形的面积和。
11.【答案】正确
【解析】【解答】解:用两个完全一样的梯形可以拼成平行四边形,这个平行四边形的面积=梯形的面积×2;
平行四边形又可以切成两个完全一样的三角形,所以用梯形面积计算公式可以计算平行四边形和三角形的面积。
故答案为:正确。
【分析】用两个完全一样的梯形可以拼成平行四边形,用两个完全一样的三角形可以拼成平行四边形,据此计算。
12.【答案】错误
【解析】【解答】解:两个面积相等的三角形,底和高不一定相等。
故答案为:错误。
【分析】三角形的面积=底×高÷2,三角形面积相等,底和高不一定相等。
13.【答案】错误
【解析】【解答】解:把一个长方形框拉成平行四边形,面积变小,周长不变。原题说法错误。
故答案为:错误。
【分析】把一个长方形框拉成平行四边形,四条边的长度是不变的,所以周长不变。长方形的宽比平行四边形的高长,所以平行四边形的面积就小于长方形的面积,面积是变小的。
14.【答案】正确
【解析】【解答】解:三角形的面积=底×高÷2,只要三角形的底与高相等,面积就相等。
故答案为:正确。
【分析】同底等高的三角形,面积相等。
15.【答案】正确
【解析】【解答】解:周长相等的长方形和平行四边形,面积不一定相等,说法正确。
故答案为:正确。
【分析】长方形的面积=长×宽,平行四边形的面积=底×高,周长相等的长方形和平行四边形,可将长方形拉成一个平行四边形,即这个过程中高减小,长方形的面积大于平行四边形的面积,本题据此解答。
16.【答案】错误
【解析】【解答】解:假设长方形、正方形、圆,它们的周长为12.56厘米;
①长方形的长可以为3.13厘米,宽为3.15厘米,面积是:
3.13×3.15=9.8595(平方厘米);
②正方形的边长为3.14厘米,面积是:
3.14×3.14=9.8596(平方厘米);
③圆的面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
④三角形的底约4.19厘米,高约是3.62厘米
4.19×3.62÷2
=15.1678÷2
=7.5839(平方厘米)
12.56平方厘米>9.8596平方厘米>9.8595平方厘米>7.5839平方厘米。
故答案为:错误。
【分析】周长相等的长方形、正方形、圆、三角形,其中圆的面积最大。
17.【答案】4
【解析】【解答】解:4÷1=4。
故答案为:4。
【分析】把整个长方形平均分成了4份,阴影部分占1份,所以整个长方形面积是阴影部分面积的4倍。
18.【答案】5公顷300平方米<53000平方米<53公顷<5平方千米
【解析】【解答】解:5公顷300平方米=50000平方米+300平方米=50300平方米,
53公顷=530000平方米,
5平方千米=5000000平方米,
50300平方米<53000平方米<53公顷<5平方千米
即:5公顷300平方米<53000平方米<53公顷<5平方千米
故答案为:5公顷300平方米<53000平方米<53公顷<5平方千米。
【分析】1平方千米=1000000平方米;1平方千米=100公顷;1公顷=10000平方米;把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
19.【答案】m2;公顷;dm2;km2
【解析】【解答】解:①一间教室的占地面积约为501平方米 ②一个学校操场的占地面积约为12公顷
③数学书的封面面积大约是53平方分米 ④成都市的总面积约为 14335平方千米
故答案为:平方米;公顷;平方分米;平方千米。
【分析】根据生活经验以及对面积单位和数据大小的认识,结合实际情况选择合适的单位即可。
20.【答案】25
【解析】【解答】解:
12.5×2=25(平方分米)
故答案为:25
【分析】根据三角形的面积=底×高÷2,平行四边形的面积=底×高,因为三角形和平行四边形等底等高,则三角形的面积是平行四边形的面积的一半,由此即可求出平行四边形的面积。
21.【答案】13
【解析】【解答】解:8×4-1×8÷2-2×3÷2-6×4÷2
=32-4-3-12
=13;
故答案为:13。
【分析】三角形ABC的面积等于长方形的面积减去三个直角三角形的面积,据此求解。
22.【答案】1
【解析】【解答】解:设A图形的高为h,根据图形所示,可得
A面积为:(3+5)×h÷2=4h
图①面积为:6×h÷2=3h
图②面积为:6×h=6h
图③面积为:4×h=4h
所以与图形A 面积相等的图形有1个。
故答案为:1
【分析】由图可知,这些图形的高相同,假设高为h,根据梯形、三角形、平行四边形面积公式,分别求出其面积,即可判断
23.【答案】27平方厘米;3
【解析】【解答】解:6÷2=3(厘米)
(3+6)×6÷2
=9×6÷2
=54÷2
=27(平方厘米)
3×6÷2
=18÷2
=9(平方厘米)
27÷9=3
故答案为:27平方厘米;3。
【分析】梯形的面积=(上底+下底)×高÷2;其中,上底=正方形的边长÷2,下底、高=正方形的边长;三角形的面积=底×高÷2;梯形是三角形面积的倍数=梯形的面积÷三角形的面积。
24.【答案】8
【解析】【解答】[30+(30+20)]×40÷2÷200=8(棵)
故答案为:8.
【分析】根据梯形面积计算公式求出梯形地的面积,再用梯形地的面积除以种树的棵数即可.
25.【答案】22.5
【解析】【解答】解:BD=(6÷4)×AD=1.5×AD,
6×(4+6)÷2=30(cm2),
①的面积=7.5 cm2,
阴影部分的面积=30-7.5=22.5(cm2)。
故答案为:22.5。
【分析】如图,连接BF、BF:
根据题意可知,图形关于直线BF对称,所以②的面积=③的面积,①的面积=④的面积,因为图①和图②等高,可以求出BD与AD的关系,可以得到②的面积=③的面积=1.5×①的面积, ②的面积+①的面积+③的面积=(1.5×2+1)×①的面积,据此先求出①的面积,再求出阴影部分的面积。
26.【答案】解:如图:
首先在相同颜色的棋子之间划出切分线,以中心点为旋转中心,旋转90°、180°、270°之后,得到一些新的切分线,同时考虑到每块包含一颗黑子和一颗白子的要求,以及每一块的面积应该是36÷4=9,即含有9个小正方格,先找到符合要求的一块后,让它绕中心旋转90°、180°、270°,便得到其他三块。
【解析】【分析】因为每一块中都要带有白子、黑子各一个.根据黑子的位置特点,先把四个黑子划分出四个部分,再根据白子的位置特点将中图形划分出四个完全相同的四个图形即可.
27.【答案】解:(70+140)×240÷2 =25200(m2)
150×200÷2=15000(m2)
25200+15000=40200(m2)
40200m2=4.02公顷
答:这个草场的占地面积是4.02公顷。
【解析】【分析】如图,,草场的占地面积=梯形面积+三角形面积,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,据此解答。
28.【答案】解:12.4×10.8÷0.16=133.92÷0.16=837(棵)答:这块地可以种白菜837棵.
【解析】【分析】根据“平行四边形面积=底×高”列式求出土地的面积,然后用土地面积除以每棵的占地面积即可求出种菜的棵数.
29.【答案】解:23×18-(23-1-1)×(18-1-1)
=414-336
=78(m2)
答:小路的占地面积是78平方米。
【解析】【分析】小路的面积=大长方形面积-小长方形面积,长方形的面积=长×宽,据此解答。
30.【答案】解:
如图,设AB的长为x厘米
8x÷2+(x+12)×12÷2=12×(8+12)÷2
4x+6x+72=12×20÷2
10x=120-72
10x=48
x=4.8
4.8×12÷2
=4.8×6
=28.8(平方厘米)
答:阴影部分的面积是28.8平方厘米。
【解析】【分析】如图:阴影部分的面积是底为AB,高为12cm的三角形的面积;设AB的长为厘米;根据三角形ABC面积+梯形ABED面积=三角形CDE的面积,列出方程,求出AB的长,然后再根据三角形的面积公式进行解答。
31.【答案】解:20000÷5÷4=1000(米)
1000米=1千米
1×1=1(平方千米)
答:这个广场的面积是1平方千米。
【解析】【分析】用共走的长度除以5求出每圈的长度,用每圈的长度除以4求出边长,把边长换算成千米,再用边长乘边长求出面积即可。
32.【答案】1公顷
33.【答案】解:18+6=24(分米)
72÷6=12(分米)
24×12=288(平方分米)
答:这个平行四边形原来的面积是288平方分米。
【解析】【分析】平行四边形的底=底边减少的长度+底边还剩的长度,平行四边形的底边减少了,高不变,面积也减少了,那么平行四边形的高=平行四边形减少了的面积÷平行四边形的底边减少的长度;平行四边形的面积=底×高。
34.【答案】解:20-6=14(米)
14×6÷2
=84÷2
=42(平方米)
答:这个梯形的面积是42平方米。
【解析】【分析】这个梯形的面积=上、下底的和×高÷2;其中,上、下底的和=绳子的长-梯形的高。
试题分析部分
1、试卷总体分布分析
总分:103分
分值分布 客观题(占比) 48.0(46.6%)
主观题(占比) 55.0(53.4%)
题量分布 客观题(占比) 23(67.6%)
主观题(占比) 11(32.4%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 9(26.5%) 26.0(25.2%)
解决问题 8(23.5%) 40.0(38.8%)
操作题 1(2.9%) 5.0(4.9%)
单选题 8(23.5%) 16.0(15.5%)
判断题 8(23.5%) 16.0(15.5%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (47.1%)
2 容易 (26.5%)
3 困难 (26.5%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 公顷、平方千米与平方米之间的换算与比较 13.0(12.6%) 4,5,9,18,32
2 三角形的面积 30.0(29.1%) 2,3,8,11,12,14,17,20,21,22,27,30
3 三位数乘两位数的笔算乘法 5.0(4.9%) 32
4 平面图形的切拼 5.0(4.9%) 26
5 长方形的面积 20.0(19.4%) 9,13,15,16,17,29,32
6 平方厘米、平方分米、平方米的认识与使用 8.0(7.8%) 19
7 梯形的面积 24.0(23.3%) 6,11,16,22,23,24,27,34
8 长方形的周长 4.0(3.9%) 13,15
9 公顷和平方千米的认识与使用 13.0(12.6%) 19,31
10 组合图形面积的巧算 23.0(22.3%) 10,21,22,25,26,27,29
11 平行四边形的面积 26.0(25.2%) 1,2,7,11,13,15,20,22,28,33
12 正方形的面积 12.0(11.7%) 16,26,31
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
