【中考专项特训】2026年中考数学专项提优练习:二次函数(含答案)
文档属性
| 名称 | 【中考专项特训】2026年中考数学专项提优练习:二次函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 795.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 14:06:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【中考专项特训】2026年中考数学专项提优练习:二次函数
一、选择题
1. 开口向下的抛物线经过点,则下列关系式可能成立的是( )
A. B. C. D.
2. 已知二次函数和(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )
A.2 B. C.4 D.
3.抛物线经过,,三点,且该抛物线与轴的交点位于轴两侧,则,,的大小关系是( )
A. B.
C. D.
4.如图,在中,,,为直线左侧一点.若,则的最大值为( )
A. B. C. D.
5.已知反比例函数的图象如图所示,则一次函数和二次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.已知正比例函数与二次函数的图象相交于两点.若两点的横坐标分别为,则的值为( )
A. B. C. D.
7.二次函数,当时,随的增大而减小.点,都在这个函数图象上.下列结论:①;②;③;④;⑤.正确的有( )
A.1个 B.2个 C.3个 D.4个
8.二次函数的部分图象如图所示,函数值y大于3的自变量x的取值可以是( )
A. B. C.0 D.2
9.记实数,,,中的最大数为,例如,则当函数时,x的取值范围为( )
A.01 B.0或
C.0或 D.
10.如图所示,抛物线y=ax2+bx+c的对称轴为x=,与x轴的一个交点A(,0),抛物线的顶点B纵坐标10;③3a-b=0;④4a+c<0;⑤A.2 B.3 C.4 D.5
二、填空题
11.抛物线与轴两个公共点的横坐标分别为,,且.若b,c为整数,则的可能取值为 .
12.在同一直角坐标系中,已知函数,(k为不等于零的常数).若函数的图象经过的图象的顶点,则k,c之间的数量关系为 .
13.如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下面五个结论正确的序号为 .
①; ②; ③;④;⑤时,
14.经过,两点的抛物线(为自变量)与轴有交点,则线段的长为 .
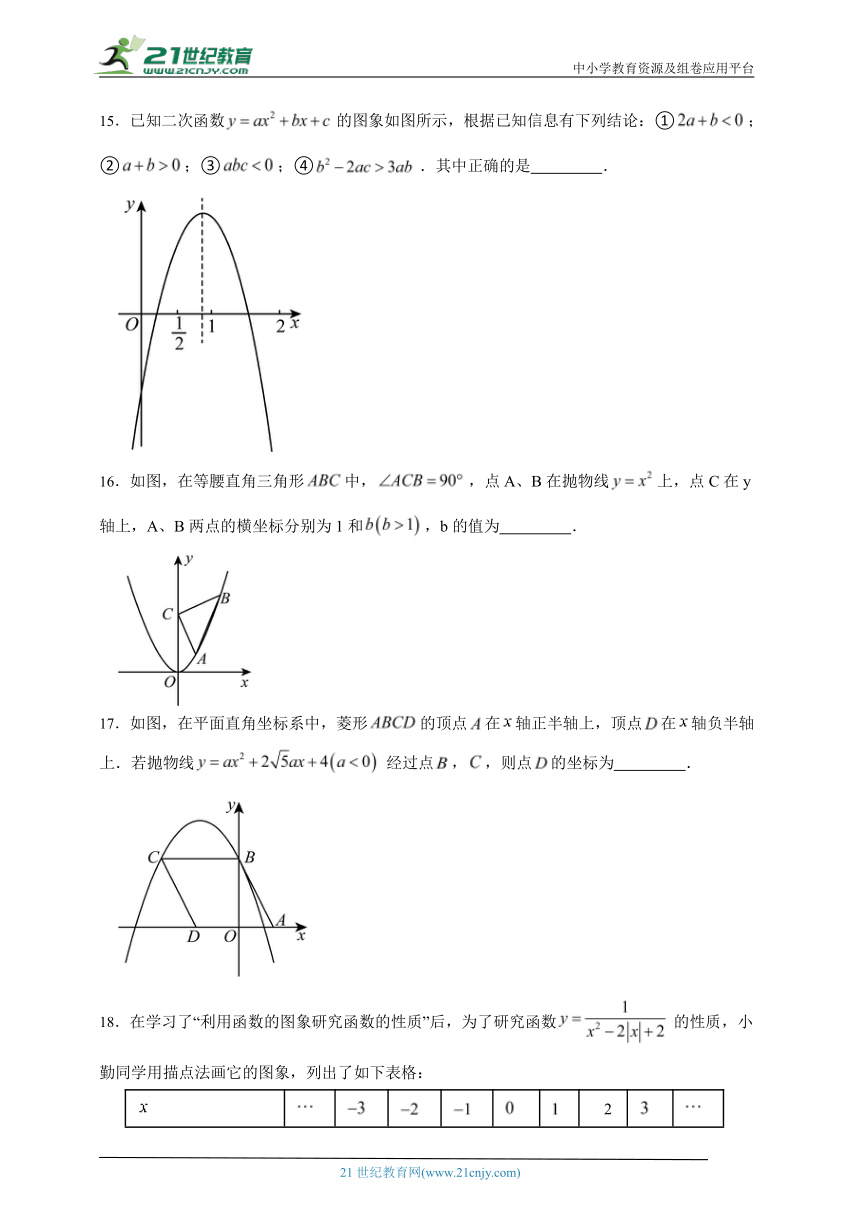
15.已知二次函数的图象如图所示,根据已知信息有下列结论:①;②;③;④.其中正确的是 .
16.如图,在等腰直角三角形中,,点A、B在抛物线上,点C在y轴上,A、B两点的横坐标分别为1和,b的值为 .
17.如图,在平面直角坐标系中,菱形的顶点在轴正半轴上,顶点在轴负半轴上.若抛物线经过点,,则点的坐标为 .
18.在学习了“利用函数的图象研究函数的性质”后,为了研究函数的性质,小勤同学用描点法画它的图象,列出了如下表格:
2
以下五个结论:①点在函数的图象上;②函数的图象一定不经过第四象限;③函数的图象关于直线对称;④点,,若,则;⑤若直线与函数的图象有个公共点,则.其中正确的结论是 .(填写序号)
三、解答题
19.在平面直角坐标系中,二次函数的表达式为 ,其中 .
(1)若此函数图象过点 (2, 5),求这个二次函数的表达式;
(2)若 , 为此二次函数图象上不同的两个点,当 时,,求 m 的值;
(3)若点 (-1, t) 在此二次函数图象上,当 时,y 随 x 的增大而增大,求 t 的取值范围.
20.如图,二次函数的图象与轴交于两点,与轴交于点.
(1)求二次函数解析式和顶点坐标.
(2)坐标平面内存在点,满足向左、向右或向下平移个单位后均落在二次函数图象上,求平移的距离.
(3)在二次函数图象上取点(不与点重合),使得在之间的图象上(含两点),该二次函数最大值与最小值的和等于1,请直接写出点的坐标.
21.已知二次函数y=x2-3x-m2+3m(m≠0的实数).
(1)二次函数图象的对称轴是 .
(2)当m=2时,
①若将平面内一点A(1,n)向右平移3a个单位,则与抛物线上的点B重合;向左平移2a个单位,则与抛物线上的点C重合,求n的值.
②如果点p(x,y)在抛物线上,且到y轴的距离小于等于2,那么我们称点p是y轴的“亲密点”,求所有“亲密点”的y的取值范围.
(3)对于二次函数图象上的两点,,当,时,均满足,直接写出t的取值范围.
22.我市某企业安排20名工人生产甲、乙两种产品,根据生产经验,每人每天生产2件甲产品或1件乙产品(每人每天只能生产一种产品).甲产品生产成本为每件10元;若安排1人生产一件乙产品,则成本为38元,以后每增加1人,平均每件乙产品成本降低2元.规定甲产品每天至少生产20件.设每天安排人生产乙产品.
(1)为了增加利润,企业须降低成本,该企业如何安排工人生产才能使得每天的生产总成本最低?最低成本是多少?
(2)该企业准备通过对外招工,增加工人数量的方式降低每天的生产总成本,那么至少招多少名工人才能实现每天的生产总成本不高于350元?
23.已知抛物线(为常数)经过点.
(1)用含的代数式表示,并求该抛物线的对称轴.
(2)当时,,求抛物线的函数表达式.
(3)在(2)的条件下,已知点在抛物线上,,求的取值范围.
24. 体育课上小林同学(抽象为一点)进行蛙跳训练,每一个完整的动作路线都可以近似地看作是抛物线的一部分.如图①是小林连续两次蛙跳的运动示意图,规定小林距离地面的竖直高度为y(m),距离起跳点的水平距离为x(m),建立如图所示的平面直角坐标系.第一个蛙跳的起跳点为原点,并在点处达到最高点,在点A处落地,落地后立即起跳进行下一个蛙跳,路线为抛物线,其开口大小和方向均与第一个蛙跳的路线抛物线相同.
(1)求小林第一个蛙跳的路线抛物线的函数解析式;
(2)若小林第二个蛙跳从时开始总处于下降状态;
①求k的值;
②在处,有一根长0.12m的海绵条垂直放置在地面,则小林在第二跳中是否会触碰到海绵条?说明理由.
(3)如图②,为提高训练效果,老师指导小林在可调节坡度的斜坡(近似看作直线)上进行训练,P为斜坡与的交点,在点Q处设置可调节支撑杆,且轴.当,且抛物线与抛物线的顶点的纵坐标恰好相等时,直接写出h的取值范围.
25.已知,是抛物线上的两点.
(1)当A为时,求抛物线的对称轴(用含a的式子表示).
(2)当时,对于,,都有,求a的取值范围.
(3)如图,若A为,B为,C为抛物线与y轴交点,点D在y轴负半轴,且,点Q在抛物线上,,E,F分别为边,上的动点,且,记的最小值为m,点P为第二象限抛物线上的一动点,,求k的取值范围.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】
13.【答案】②③④⑤
14.【答案】
15.【答案】①②④
16.【答案】2
17.【答案】
18.【答案】①②④
19.【答案】(1)解: 把点 (2,5) 代入到二次函数的表达式 中,得: .
化简得: ,联立方程组:
,
解得:
所以二次函数的表达式为 ;
(2)解:∵,∴,∴.
∵,∴,解得:
(3)解:由题意得: 且 ,解得: .
由 ,把 (-1,t) 代入整理得 ,∴.
20.【答案】(1)解:∵ 二次函数的图象与轴交于两点,
∴将点A和点B的坐标代入可得:,
解得:,
∴二次函数的解析式为:,
∵,
∴顶点坐标为(1,-4).
(2)解:∵ 点P满足向左、向右或向下平移个单位后均落在二次函数图象上,
∴点P在对称轴上,
设P(1,m-4),
∴点P向右平移m个单位后的坐标为(m+1,m-4),
∴,
解得:m=0(舍去)或m=1,
即平移的距离m=1.
(3)解:点D的坐标为或.
21.【答案】(1)直线x=
(2)解: 当 时,二次函数的解析式为 ,
①∵将平面内一点A(1,n)向右平移3a个单位,则与抛物线上的点B重合,向左平移2a个单位,则与抛物线上的点C重合,
∴点 ,
由(1)可知:二次函数图象的对称轴是直线 ,
∵点. )都在二次函数
的图象上,
解得:,
∴点( ,
当 时,;
②∵二次函数的解析式为
,
当 时,y取得最小值 当 时, ,
当 时, ,
,
∴抛物线的开口向上,
∴所有“亲密点”的y的取值范围是
(3)解:由(1)可知:二次函数图象的对称轴是直线 ,
∴当 时,y随x增大而减小;当 时, y随x增大而增大,
设点 在二次函数 的图象上,且满足 ,
当 时,
3m,
∴当 时,
,
∵对于二次函数图象上的两点.
当 时,均满足 ,
∴当点 在点 下方时,满足条件 ,
整理, 得: ,
解得: ,
,
∴抛物线的开口向上,
,
解得:,
∴t的取值范围是
22.【答案】(1)当安排10名工人生产甲产品,10名工人生产乙产品时才能使得每天的生产总成本最低,最低成本是400元
(2)至少招5名工人才能实现每天的生产总成本不高于350元
23.【答案】(1)解:∵抛物线经过点,
∴,
解得,,
∴抛物线解析式为(为常数),
∴对称轴直线为;
(2)解:当时,图象开口向上,
∵抛物线对称轴直线为,
∴当时,随的增大而减小,
∴当时,,
∴,
解得:(舍去);
当时,图象开口向下,当时,随的增大而增大,
∴当时,,
∴,
解得:,
∴,
∴抛物线解析式为:;
(3)解:∵抛物线解析式为,
∴对称轴直线为,图象开口向下,
∴当时,随的增大而增大,
当时,随的增大而减小,
∴点关于对称轴直线对称的点为,
∵,
∴,
解得:,
∴,
∴当时,,
当时,,
当时,,
∴.
24.【答案】(1)解:(1)由题意知抛物线的顶点为(1,0.4),且过原点(0,0)
设解析式为,将(0,0)代入得
a+0.4=0,得a=-0.4
故抛物线的解析式为
(2)解:①由(1),令y=0,则x=0或x=2,即知A(2,0)
由题意知中a=-0.4且过点(2,0)
得,将(2,0)代入得
同时x>2.6时总处于下降状态,故h=2.6,代入上式得
解得;
②L2:,令x=3,则y==0.08<0.12
故小林会碰到海绵条
(3)解:由题意知L2的顶点坐标为(h,0.4),故
当m=时,联立解得或(舍去),故点P()
将点P代入L2解析式得解得h=1(舍)或h=
当m=时,联立解得或(舍去),故点P()
将点P代入L2解析式得解得h=1(舍)或h=2
故
25.【答案】(1)直线
(2)或
(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考专项特训】2026年中考数学专项提优练习:二次函数
一、选择题
1. 开口向下的抛物线经过点,则下列关系式可能成立的是( )
A. B. C. D.
2. 已知二次函数和(m是常数)的图象与x轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )
A.2 B. C.4 D.
3.抛物线经过,,三点,且该抛物线与轴的交点位于轴两侧,则,,的大小关系是( )
A. B.
C. D.
4.如图,在中,,,为直线左侧一点.若,则的最大值为( )
A. B. C. D.
5.已知反比例函数的图象如图所示,则一次函数和二次函数在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
6.已知正比例函数与二次函数的图象相交于两点.若两点的横坐标分别为,则的值为( )
A. B. C. D.
7.二次函数,当时,随的增大而减小.点,都在这个函数图象上.下列结论:①;②;③;④;⑤.正确的有( )
A.1个 B.2个 C.3个 D.4个
8.二次函数的部分图象如图所示,函数值y大于3的自变量x的取值可以是( )
A. B. C.0 D.2
9.记实数,,,中的最大数为,例如,则当函数时,x的取值范围为( )
A.01 B.0或
C.0或 D.
10.如图所示,抛物线y=ax2+bx+c的对称轴为x=,与x轴的一个交点A(,0),抛物线的顶点B纵坐标1
二、填空题
11.抛物线与轴两个公共点的横坐标分别为,,且.若b,c为整数,则的可能取值为 .
12.在同一直角坐标系中,已知函数,(k为不等于零的常数).若函数的图象经过的图象的顶点,则k,c之间的数量关系为 .
13.如图,二次函数的图象与轴交于点,与轴交于点,对称轴为直线,下面五个结论正确的序号为 .
①; ②; ③;④;⑤时,
14.经过,两点的抛物线(为自变量)与轴有交点,则线段的长为 .
15.已知二次函数的图象如图所示,根据已知信息有下列结论:①;②;③;④.其中正确的是 .
16.如图,在等腰直角三角形中,,点A、B在抛物线上,点C在y轴上,A、B两点的横坐标分别为1和,b的值为 .
17.如图,在平面直角坐标系中,菱形的顶点在轴正半轴上,顶点在轴负半轴上.若抛物线经过点,,则点的坐标为 .
18.在学习了“利用函数的图象研究函数的性质”后,为了研究函数的性质,小勤同学用描点法画它的图象,列出了如下表格:
2
以下五个结论:①点在函数的图象上;②函数的图象一定不经过第四象限;③函数的图象关于直线对称;④点,,若,则;⑤若直线与函数的图象有个公共点,则.其中正确的结论是 .(填写序号)
三、解答题
19.在平面直角坐标系中,二次函数的表达式为 ,其中 .
(1)若此函数图象过点 (2, 5),求这个二次函数的表达式;
(2)若 , 为此二次函数图象上不同的两个点,当 时,,求 m 的值;
(3)若点 (-1, t) 在此二次函数图象上,当 时,y 随 x 的增大而增大,求 t 的取值范围.
20.如图,二次函数的图象与轴交于两点,与轴交于点.
(1)求二次函数解析式和顶点坐标.
(2)坐标平面内存在点,满足向左、向右或向下平移个单位后均落在二次函数图象上,求平移的距离.
(3)在二次函数图象上取点(不与点重合),使得在之间的图象上(含两点),该二次函数最大值与最小值的和等于1,请直接写出点的坐标.
21.已知二次函数y=x2-3x-m2+3m(m≠0的实数).
(1)二次函数图象的对称轴是 .
(2)当m=2时,
①若将平面内一点A(1,n)向右平移3a个单位,则与抛物线上的点B重合;向左平移2a个单位,则与抛物线上的点C重合,求n的值.
②如果点p(x,y)在抛物线上,且到y轴的距离小于等于2,那么我们称点p是y轴的“亲密点”,求所有“亲密点”的y的取值范围.
(3)对于二次函数图象上的两点,,当,时,均满足,直接写出t的取值范围.
22.我市某企业安排20名工人生产甲、乙两种产品,根据生产经验,每人每天生产2件甲产品或1件乙产品(每人每天只能生产一种产品).甲产品生产成本为每件10元;若安排1人生产一件乙产品,则成本为38元,以后每增加1人,平均每件乙产品成本降低2元.规定甲产品每天至少生产20件.设每天安排人生产乙产品.
(1)为了增加利润,企业须降低成本,该企业如何安排工人生产才能使得每天的生产总成本最低?最低成本是多少?
(2)该企业准备通过对外招工,增加工人数量的方式降低每天的生产总成本,那么至少招多少名工人才能实现每天的生产总成本不高于350元?
23.已知抛物线(为常数)经过点.
(1)用含的代数式表示,并求该抛物线的对称轴.
(2)当时,,求抛物线的函数表达式.
(3)在(2)的条件下,已知点在抛物线上,,求的取值范围.
24. 体育课上小林同学(抽象为一点)进行蛙跳训练,每一个完整的动作路线都可以近似地看作是抛物线的一部分.如图①是小林连续两次蛙跳的运动示意图,规定小林距离地面的竖直高度为y(m),距离起跳点的水平距离为x(m),建立如图所示的平面直角坐标系.第一个蛙跳的起跳点为原点,并在点处达到最高点,在点A处落地,落地后立即起跳进行下一个蛙跳,路线为抛物线,其开口大小和方向均与第一个蛙跳的路线抛物线相同.
(1)求小林第一个蛙跳的路线抛物线的函数解析式;
(2)若小林第二个蛙跳从时开始总处于下降状态;
①求k的值;
②在处,有一根长0.12m的海绵条垂直放置在地面,则小林在第二跳中是否会触碰到海绵条?说明理由.
(3)如图②,为提高训练效果,老师指导小林在可调节坡度的斜坡(近似看作直线)上进行训练,P为斜坡与的交点,在点Q处设置可调节支撑杆,且轴.当,且抛物线与抛物线的顶点的纵坐标恰好相等时,直接写出h的取值范围.
25.已知,是抛物线上的两点.
(1)当A为时,求抛物线的对称轴(用含a的式子表示).
(2)当时,对于,,都有,求a的取值范围.
(3)如图,若A为,B为,C为抛物线与y轴交点,点D在y轴负半轴,且,点Q在抛物线上,,E,F分别为边,上的动点,且,记的最小值为m,点P为第二象限抛物线上的一动点,,求k的取值范围.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】A
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】
13.【答案】②③④⑤
14.【答案】
15.【答案】①②④
16.【答案】2
17.【答案】
18.【答案】①②④
19.【答案】(1)解: 把点 (2,5) 代入到二次函数的表达式 中,得: .
化简得: ,联立方程组:
,
解得:
所以二次函数的表达式为 ;
(2)解:∵,∴,∴.
∵,∴,解得:
(3)解:由题意得: 且 ,解得: .
由 ,把 (-1,t) 代入整理得 ,∴.
20.【答案】(1)解:∵ 二次函数的图象与轴交于两点,
∴将点A和点B的坐标代入可得:,
解得:,
∴二次函数的解析式为:,
∵,
∴顶点坐标为(1,-4).
(2)解:∵ 点P满足向左、向右或向下平移个单位后均落在二次函数图象上,
∴点P在对称轴上,
设P(1,m-4),
∴点P向右平移m个单位后的坐标为(m+1,m-4),
∴,
解得:m=0(舍去)或m=1,
即平移的距离m=1.
(3)解:点D的坐标为或.
21.【答案】(1)直线x=
(2)解: 当 时,二次函数的解析式为 ,
①∵将平面内一点A(1,n)向右平移3a个单位,则与抛物线上的点B重合,向左平移2a个单位,则与抛物线上的点C重合,
∴点 ,
由(1)可知:二次函数图象的对称轴是直线 ,
∵点. )都在二次函数
的图象上,
解得:,
∴点( ,
当 时,;
②∵二次函数的解析式为
,
当 时,y取得最小值 当 时, ,
当 时, ,
,
∴抛物线的开口向上,
∴所有“亲密点”的y的取值范围是
(3)解:由(1)可知:二次函数图象的对称轴是直线 ,
∴当 时,y随x增大而减小;当 时, y随x增大而增大,
设点 在二次函数 的图象上,且满足 ,
当 时,
3m,
∴当 时,
,
∵对于二次函数图象上的两点.
当 时,均满足 ,
∴当点 在点 下方时,满足条件 ,
整理, 得: ,
解得: ,
,
∴抛物线的开口向上,
,
解得:,
∴t的取值范围是
22.【答案】(1)当安排10名工人生产甲产品,10名工人生产乙产品时才能使得每天的生产总成本最低,最低成本是400元
(2)至少招5名工人才能实现每天的生产总成本不高于350元
23.【答案】(1)解:∵抛物线经过点,
∴,
解得,,
∴抛物线解析式为(为常数),
∴对称轴直线为;
(2)解:当时,图象开口向上,
∵抛物线对称轴直线为,
∴当时,随的增大而减小,
∴当时,,
∴,
解得:(舍去);
当时,图象开口向下,当时,随的增大而增大,
∴当时,,
∴,
解得:,
∴,
∴抛物线解析式为:;
(3)解:∵抛物线解析式为,
∴对称轴直线为,图象开口向下,
∴当时,随的增大而增大,
当时,随的增大而减小,
∴点关于对称轴直线对称的点为,
∵,
∴,
解得:,
∴,
∴当时,,
当时,,
当时,,
∴.
24.【答案】(1)解:(1)由题意知抛物线的顶点为(1,0.4),且过原点(0,0)
设解析式为,将(0,0)代入得
a+0.4=0,得a=-0.4
故抛物线的解析式为
(2)解:①由(1),令y=0,则x=0或x=2,即知A(2,0)
由题意知中a=-0.4且过点(2,0)
得,将(2,0)代入得
同时x>2.6时总处于下降状态,故h=2.6,代入上式得
解得;
②L2:,令x=3,则y==0.08<0.12
故小林会碰到海绵条
(3)解:由题意知L2的顶点坐标为(h,0.4),故
当m=时,联立解得或(舍去),故点P()
将点P代入L2解析式得解得h=1(舍)或h=
当m=时,联立解得或(舍去),故点P()
将点P代入L2解析式得解得h=1(舍)或h=2
故
25.【答案】(1)直线
(2)或
(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
