【中考专项特训】2026年中考数学专项提优练习:四边形(含答案)
文档属性
| 名称 | 【中考专项特训】2026年中考数学专项提优练习:四边形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 14:04:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【中考专项特训】2026年中考数学专项提优练习:四边形
一、选择题
1.在中,,平分且交于点E,点F在边上,.则的度数为( )
A. B. C. D.
2.如图,在菱形中,点是的中点,对角线,相交于点,连接,若菱形的周长是,则长为( )
A. B. C. D.
3.如图,在中,对角线,相交于点,若,则的长为( )
A. B. C. D.
4.如图,取两根长度不等的细木棒,,将它们的中点重合固定(记为点).转动木棒,在由锐角变成钝角的过程中,分析以木棒四个端点为顶点的四边形,下列结论一定成立的是( )
A. B.
C. D.
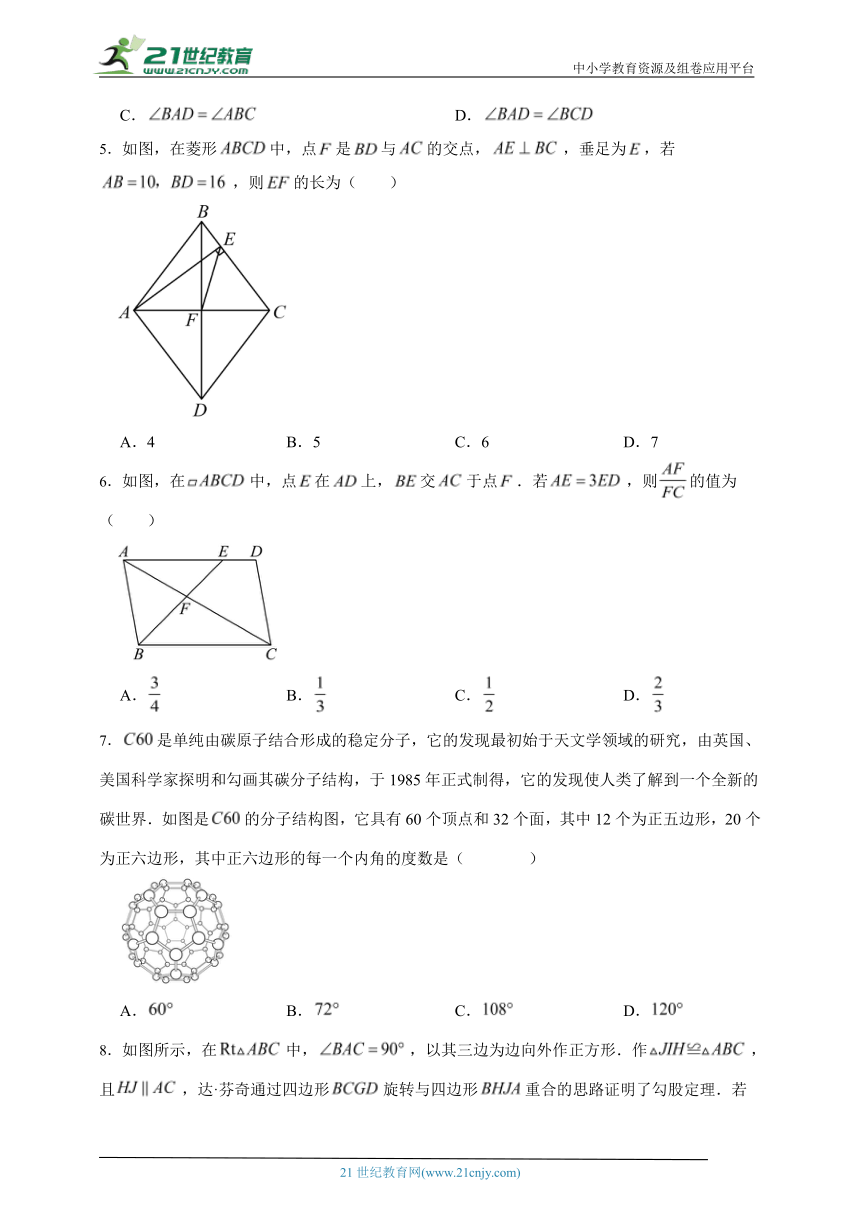
5.如图,在菱形中,点是与的交点,,垂足为,若,则的长为( )
A.4 B.5 C.6 D.7
6.如图,在中,点在上,交于点.若,则的值为( )
A. B. C. D.
7.是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A. B. C. D.
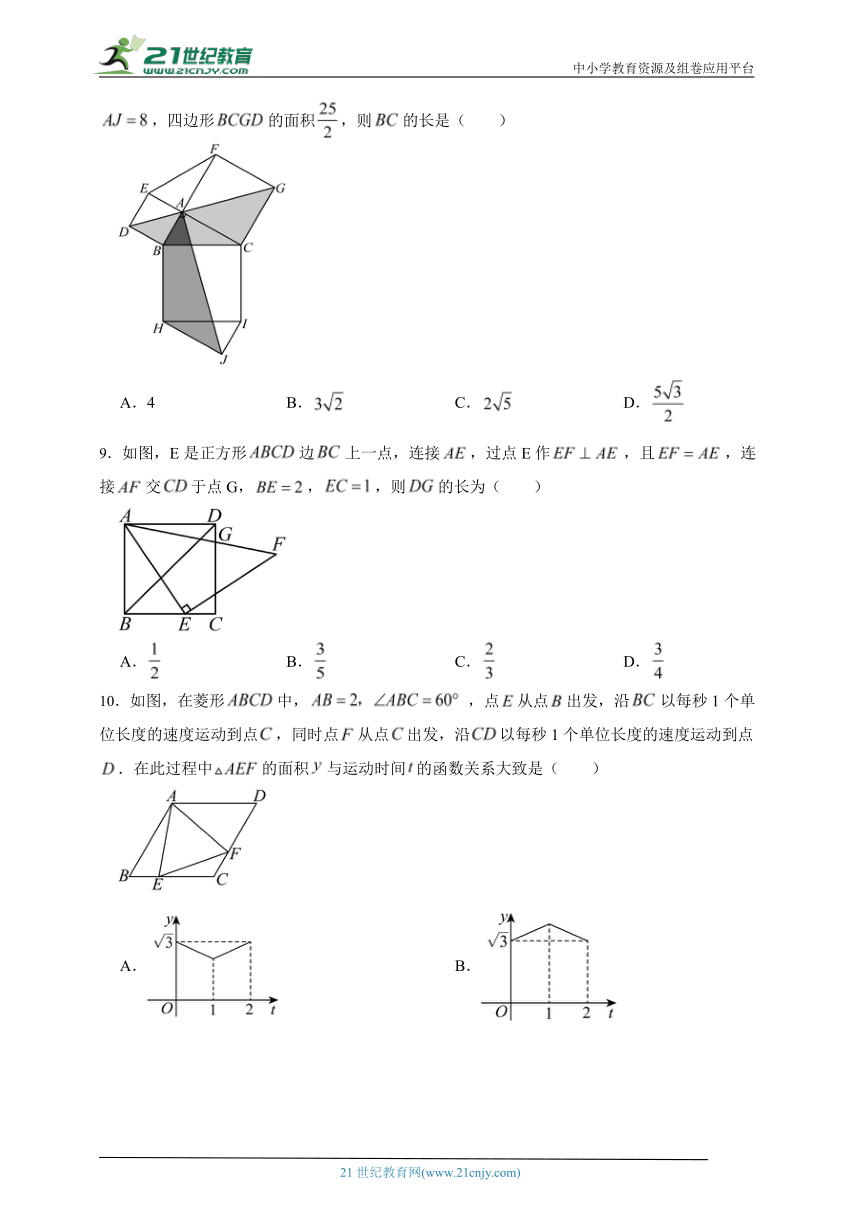
8.如图所示,在中,,以其三边为边向外作正方形.作,且,达·芬奇通过四边形旋转与四边形重合的思路证明了勾股定理.若,四边形的面积,则的长是( )
A.4 B. C. D.
9.如图,E是正方形边上一点,连接,过点E作,且,连接交于点G,,,则的长为( )
A. B. C. D.
10.如图,在菱形中,,点从点出发,沿以每秒1个单位长度的速度运动到点,同时点从点出发,沿以每秒1个单位长度的速度运动到点.在此过程中的面积与运动时间的函数关系大致是( )
A. B.
C. D.
二、填空题
11.在平面直角坐标系中,点在抛物线上运动,过点作轴于点,以为对角线作矩形,连接,则对角线的最小值为 .
12.如图,正方形的边长为2,点E在边上运动,连接并绕点D逆时针旋转得到,点E运动过程中,的最小值为 .
13.如图,在正方形中,为对角线上一点,,过点作,交于点,的延长线交于点,则 ;若,则的长等于 .
14.如图,在边长为4的菱形中,,是上的一点,将沿翻折得到,交于点.若,则的值为 .
15.如图,将平行四边形绕点A旋转得到平行四边形,点落在边上,若,当B、、三点共线时,等于 .
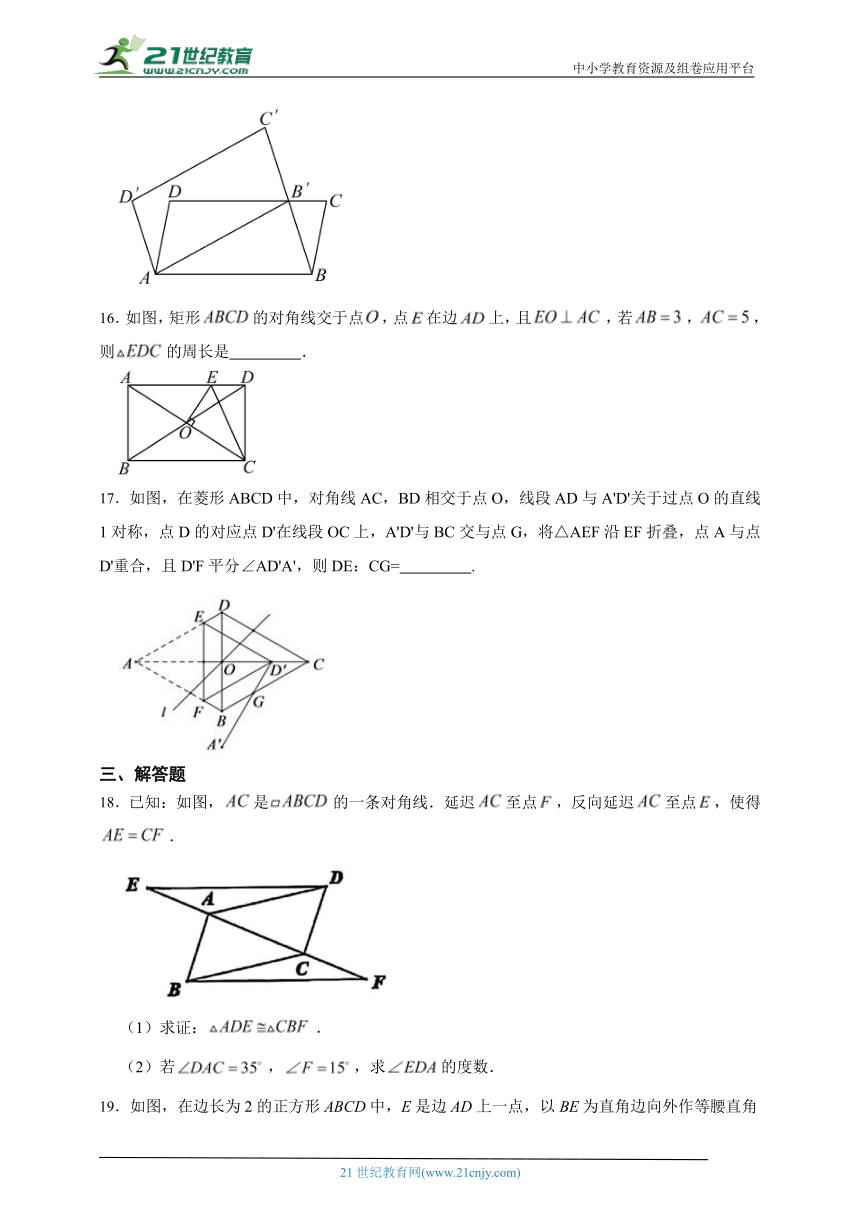
16.如图,矩形的对角线交于点,点在边上,且,若,,则的周长是 .
17.如图,在菱形ABCD中,对角线AC,BD相交于点O,线段AD与A'D'关于过点O的直线1对称,点D的对应点D'在线段OC上,A'D'与BC交与点G,将△AEF沿EF折叠,点A与点D'重合,且D'F平分∠AD'A',则DE:CG= .
三、解答题
18.已知:如图,是的一条对角线.延迟至点,反向延迟至点,使得.
(1)求证:.
(2)若,,求的度数.
19.如图,在边长为2的正方形ABCD中,E是边AD上一点,以BE为直角边向外作等腰直角三角形BEF,且∠BEF=90°,BF和EF分别交CD于点M,N.解答下列问题:
(1)当E为AD中点时,求DN,CM的长;
(2)当CM=DN时,求AE的长.
20.如图1是某路政部门正在维修路灯的实物图片,可抽象为如图2是其平面示意图.路灯和汽车折臂升降机的折臂底座都垂直于地面,且它们之间的水平距离,折臂底座高.上折臂与下折臂的夹角,下折臂与折臂底座的夹角,下折臂端点到地面距离是.(结果精确到,参考数据:,,,)
(1)求下折臂的长;
(2)求路灯的高.
21.为保护青少年视力,某企业研发了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意(如图2),测得底座高为,,支架为,面板长为,为厚度忽略不计)
(1)求支点C离桌面l的高度为多少?(结果保留根号)
(2)当面板绕点C转动时,面板与桌面的夹角满足时,保护视力的效果较好.当从变化到的过程中,面板上端E离桌面l的高度增加了多少?结果精确到,参考数据:,,)
22.定义:两组邻边分别相等的四边形叫做“筝形”.
(1)如图1,在菱形中,E是的中点,连接,将沿翻折到,延长交于点P,请写出图中的所有“筝形”;
(2)如图2,将(1)中的“菱形”改为“正方形”其他条件不变,求的值;
(3)如图3,在矩形中,是边的中点,连接,将沿翻折到,点P是线段上一点,若四边形是“筝形”,请直接写出的长.
23.综合与探究
【定义】若四边形的一条对角线将这个四边形分成等腰三角形和直角三角形,且此对角线为直角三角形的斜边,则这个四边形叫做“等腰直角四边形”,这条对角线为“分割对角线”.
【示例】如图1,是四边形的对角线,是等腰三角形,,则四边形是等腰直角四边形,是分割对角线.
【简单应用】
(1)如图2,在“等腰直角四边形”中,,.若,,,则___________;
(2)如图3,在中,点在对角线上.若四边形是“等腰直角四边形”,,求的值;
【拓展提升】
(3)如图4,在“等腰直角四边形”中,对角线与相关于点,,,求的值;
(4)如图5,在中,,,.点是平面内一点且满足四边形是以为分割对角线的“等腰直角四边形”,与交于点,直接写出的值.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】5
12.【答案】
13.【答案】;
14.【答案】
15.【答案】
16.【答案】7
17.【答案】1:3
18.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∴∠ACB=∠CAD,
∵∠BCF=180°-ACB,∠DAE=180°-∠CAD,
∴∠DAE=∠BCF,
∵在△ADE和△CBF中,AD=BC,∠DAE=∠BCF,AE=CF,
∴△ADE≌△CBF(SAS).
(2)解:∵△ADE≌△CBF,
∴∠E=∠F=15°,
∵∠DAC=35°,
∴∠EDA=∠DAC-∠E=20°.
19.【答案】(1)解:∵四边形ABCD是边长为2的正方形,E为AD中点,
∴AE=ED=1,
∵△BEF是等腰直角三角形,∠BEF=90°,
∴∠AEB+∠DEF=90°,
又∵正方形ABCD中,∠A=∠D=90°,∠AEB+∠ABE=90°,
∴∠ABE=∠DEF
∴△ABE~△DEN
∴
∴DN=,
∵∠A=∠C=90°,∠ABE+∠CBM=45°,∠AEB+∠ABE=90°,∠BEC+∠AEB=180°,∠BEC=135°,∠EBC+∠ECB=45°,
∴∠ABE=∠MBC,
∴△BCM~△BAE
∴
∴CM=
(2)解:设AE=x,则ED=2-x,CM=DN=y,则DM=2-y,
由(1)可知,△ABE~△DEN,△BCM~△BAE,
∴,,
即,,
将代入中,
得到
解得(舍去不合理的根)
∴AE=
20.【答案】(1)
(2)
21.【答案】(1)解:过点C作于点F,过点B作于点M,
∴.
由题意得:,
∴四边形为矩形,
∴.
∵,
∴.
∵,
∴.
∴,
答:支点C离桌面l的高度为;
(2)解:过点C作过点E作于点H,
∴.
∵,
∴,
当时,;
当时,;
∴,
∴当α从变化到的过程中,面板上端E离桌面l的高度增加了约.
22.【答案】(1)
(2)
(3)
23.【答案】(1);(2);(3);(4)或或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考专项特训】2026年中考数学专项提优练习:四边形
一、选择题
1.在中,,平分且交于点E,点F在边上,.则的度数为( )
A. B. C. D.
2.如图,在菱形中,点是的中点,对角线,相交于点,连接,若菱形的周长是,则长为( )
A. B. C. D.
3.如图,在中,对角线,相交于点,若,则的长为( )
A. B. C. D.
4.如图,取两根长度不等的细木棒,,将它们的中点重合固定(记为点).转动木棒,在由锐角变成钝角的过程中,分析以木棒四个端点为顶点的四边形,下列结论一定成立的是( )
A. B.
C. D.
5.如图,在菱形中,点是与的交点,,垂足为,若,则的长为( )
A.4 B.5 C.6 D.7
6.如图,在中,点在上,交于点.若,则的值为( )
A. B. C. D.
7.是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A. B. C. D.
8.如图所示,在中,,以其三边为边向外作正方形.作,且,达·芬奇通过四边形旋转与四边形重合的思路证明了勾股定理.若,四边形的面积,则的长是( )
A.4 B. C. D.
9.如图,E是正方形边上一点,连接,过点E作,且,连接交于点G,,,则的长为( )
A. B. C. D.
10.如图,在菱形中,,点从点出发,沿以每秒1个单位长度的速度运动到点,同时点从点出发,沿以每秒1个单位长度的速度运动到点.在此过程中的面积与运动时间的函数关系大致是( )
A. B.
C. D.
二、填空题
11.在平面直角坐标系中,点在抛物线上运动,过点作轴于点,以为对角线作矩形,连接,则对角线的最小值为 .
12.如图,正方形的边长为2,点E在边上运动,连接并绕点D逆时针旋转得到,点E运动过程中,的最小值为 .
13.如图,在正方形中,为对角线上一点,,过点作,交于点,的延长线交于点,则 ;若,则的长等于 .
14.如图,在边长为4的菱形中,,是上的一点,将沿翻折得到,交于点.若,则的值为 .
15.如图,将平行四边形绕点A旋转得到平行四边形,点落在边上,若,当B、、三点共线时,等于 .
16.如图,矩形的对角线交于点,点在边上,且,若,,则的周长是 .
17.如图,在菱形ABCD中,对角线AC,BD相交于点O,线段AD与A'D'关于过点O的直线1对称,点D的对应点D'在线段OC上,A'D'与BC交与点G,将△AEF沿EF折叠,点A与点D'重合,且D'F平分∠AD'A',则DE:CG= .
三、解答题
18.已知:如图,是的一条对角线.延迟至点,反向延迟至点,使得.
(1)求证:.
(2)若,,求的度数.
19.如图,在边长为2的正方形ABCD中,E是边AD上一点,以BE为直角边向外作等腰直角三角形BEF,且∠BEF=90°,BF和EF分别交CD于点M,N.解答下列问题:
(1)当E为AD中点时,求DN,CM的长;
(2)当CM=DN时,求AE的长.
20.如图1是某路政部门正在维修路灯的实物图片,可抽象为如图2是其平面示意图.路灯和汽车折臂升降机的折臂底座都垂直于地面,且它们之间的水平距离,折臂底座高.上折臂与下折臂的夹角,下折臂与折臂底座的夹角,下折臂端点到地面距离是.(结果精确到,参考数据:,,,)
(1)求下折臂的长;
(2)求路灯的高.
21.为保护青少年视力,某企业研发了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意(如图2),测得底座高为,,支架为,面板长为,为厚度忽略不计)
(1)求支点C离桌面l的高度为多少?(结果保留根号)
(2)当面板绕点C转动时,面板与桌面的夹角满足时,保护视力的效果较好.当从变化到的过程中,面板上端E离桌面l的高度增加了多少?结果精确到,参考数据:,,)
22.定义:两组邻边分别相等的四边形叫做“筝形”.
(1)如图1,在菱形中,E是的中点,连接,将沿翻折到,延长交于点P,请写出图中的所有“筝形”;
(2)如图2,将(1)中的“菱形”改为“正方形”其他条件不变,求的值;
(3)如图3,在矩形中,是边的中点,连接,将沿翻折到,点P是线段上一点,若四边形是“筝形”,请直接写出的长.
23.综合与探究
【定义】若四边形的一条对角线将这个四边形分成等腰三角形和直角三角形,且此对角线为直角三角形的斜边,则这个四边形叫做“等腰直角四边形”,这条对角线为“分割对角线”.
【示例】如图1,是四边形的对角线,是等腰三角形,,则四边形是等腰直角四边形,是分割对角线.
【简单应用】
(1)如图2,在“等腰直角四边形”中,,.若,,,则___________;
(2)如图3,在中,点在对角线上.若四边形是“等腰直角四边形”,,求的值;
【拓展提升】
(3)如图4,在“等腰直角四边形”中,对角线与相关于点,,,求的值;
(4)如图5,在中,,,.点是平面内一点且满足四边形是以为分割对角线的“等腰直角四边形”,与交于点,直接写出的值.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】A
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】5
12.【答案】
13.【答案】;
14.【答案】
15.【答案】
16.【答案】7
17.【答案】1:3
18.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∴∠ACB=∠CAD,
∵∠BCF=180°-ACB,∠DAE=180°-∠CAD,
∴∠DAE=∠BCF,
∵在△ADE和△CBF中,AD=BC,∠DAE=∠BCF,AE=CF,
∴△ADE≌△CBF(SAS).
(2)解:∵△ADE≌△CBF,
∴∠E=∠F=15°,
∵∠DAC=35°,
∴∠EDA=∠DAC-∠E=20°.
19.【答案】(1)解:∵四边形ABCD是边长为2的正方形,E为AD中点,
∴AE=ED=1,
∵△BEF是等腰直角三角形,∠BEF=90°,
∴∠AEB+∠DEF=90°,
又∵正方形ABCD中,∠A=∠D=90°,∠AEB+∠ABE=90°,
∴∠ABE=∠DEF
∴△ABE~△DEN
∴
∴DN=,
∵∠A=∠C=90°,∠ABE+∠CBM=45°,∠AEB+∠ABE=90°,∠BEC+∠AEB=180°,∠BEC=135°,∠EBC+∠ECB=45°,
∴∠ABE=∠MBC,
∴△BCM~△BAE
∴
∴CM=
(2)解:设AE=x,则ED=2-x,CM=DN=y,则DM=2-y,
由(1)可知,△ABE~△DEN,△BCM~△BAE,
∴,,
即,,
将代入中,
得到
解得(舍去不合理的根)
∴AE=
20.【答案】(1)
(2)
21.【答案】(1)解:过点C作于点F,过点B作于点M,
∴.
由题意得:,
∴四边形为矩形,
∴.
∵,
∴.
∵,
∴.
∴,
答:支点C离桌面l的高度为;
(2)解:过点C作过点E作于点H,
∴.
∵,
∴,
当时,;
当时,;
∴,
∴当α从变化到的过程中,面板上端E离桌面l的高度增加了约.
22.【答案】(1)
(2)
(3)
23.【答案】(1);(2);(3);(4)或或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
