【中考专项特训】2026年中考数学专项提优练习:圆(含答案)
文档属性
| 名称 | 【中考专项特训】2026年中考数学专项提优练习:圆(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 14:11:25 | ||
图片预览


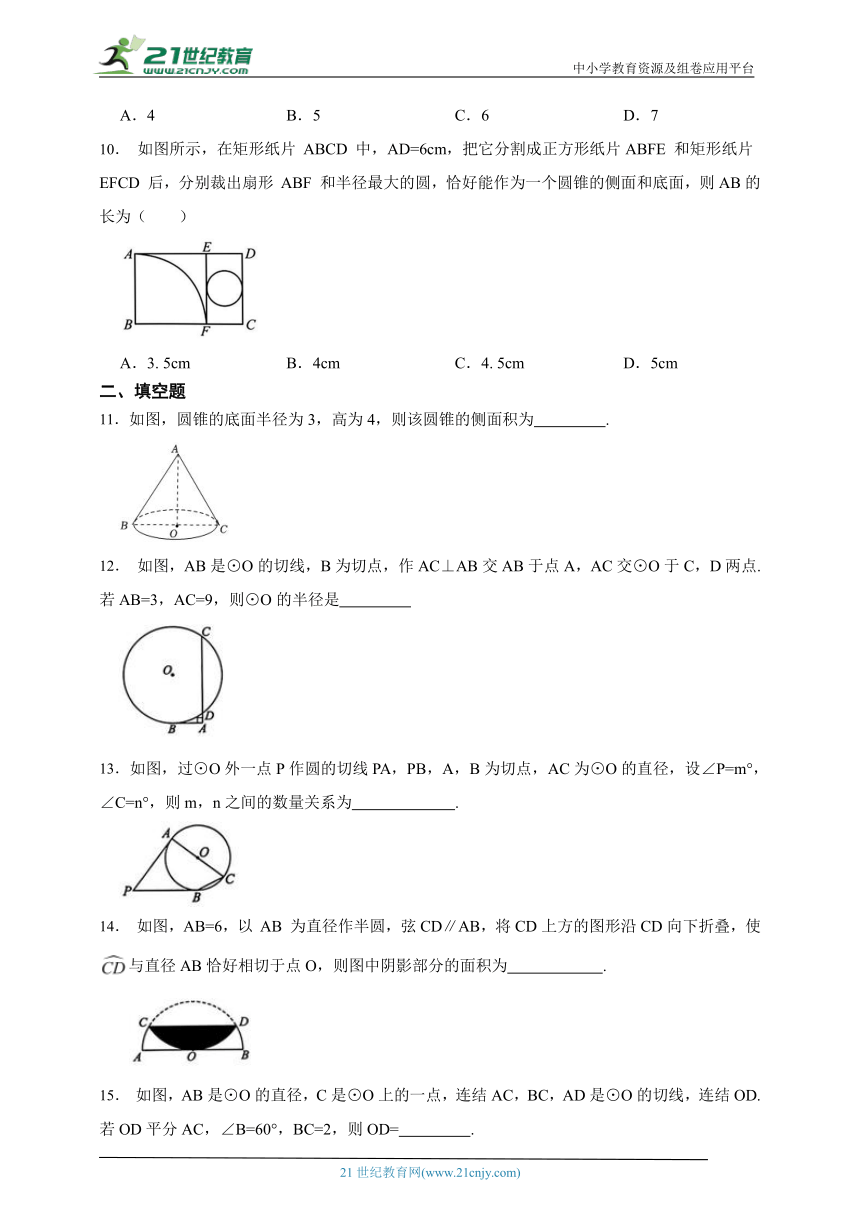
文档简介
中小学教育资源及组卷应用平台
【中考专项特训】2026年中考数学专项提优练习:圆
一、选择题
1.下列命题正确的是( )
A.三个点确定一个圆
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.同弧或等弧所对的圆周角相等
D.圆内接平行四边形一定是正方形
2. 图1是通过平面图形的镶嵌所呈现的图案,图2是其局部放大示意图,由正六边形、正方形和正三角形构成,它的轮廓为正十二边形,则图2中∠ABC的大小是( )
A.90° B.120° C.135° D.150°
3.如图,某款扫地机器人的俯视图是一个等宽曲边三角形ABC(分别以正△ABC的三个顶点 A,B,C为圆心,AB长为半径画弧得到的图形).若AB=6,则曲边AB的长为( )
A.π B.2π C.6π D.12π
4.如图,点A,B,C在⊙O上,连结OA,OC,AB,AC,BC.若∠B=135°,AC=4,则AC的长为( )
A.π B. C. D.
5. 如图,⊙O是△ABC的外接圆,AB是直径,CD平分∠ACB,AD=2,则⊙O的半径为( )
A.2 B.1 C. D.
6. 如图, AB是⊙O的直径, ∠CAB=40°, 则∠ADC的度数是( )
A.80° B.50° C.40° D.25°
7.《九章算术》是中国古代第一部数学专著,第一章“方田”中已讲述了平面几何图形面积的计算方法,比如扇形面积的计算,“今有宛田,下周三十步,径十六步,问为田几何.”大致意思为:现有一块扇形的田,弧长30步,其所在圆的直径是 16步,则这块田的面积为( )
A.120平方步 B.240平方步
C.平方步 D.π平方步
8.如图,半径为 5 的 扇 形 AOB 中,∠AOB=90°,C 是 上一点,CD⊥OA,CE⊥OB,垂足分别为 D,E.若CD=CE,则图中阴影部分的面积为( )
A. B. C. D.
9.如图所示,将半径为4的圆形纸片折叠使弧AB 经过圆心O,过点O 作直径 于点E,P是半径OD上一动点,连结AP,则AP 的长度不可能是( )
A.4 B.5 C.6 D.7
10. 如图所示,在矩形纸片 ABCD 中,AD=6cm,把它分割成正方形纸片ABFE 和矩形纸片EFCD 后,分别裁出扇形 ABF 和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A.3. 5cm B.4cm C.4. 5cm D.5cm
二、填空题
11.如图,圆锥的底面半径为3,高为4,则该圆锥的侧面积为 .
12. 如图,AB是⊙O的切线,B为切点,作AC⊥AB交AB于点A,AC交⊙O于C,D两点.若AB=3,AC=9,则⊙O的半径是
13.如图,过⊙O外一点P作圆的切线PA,PB,A,B为切点,AC为⊙O的直径,设∠P=m°,∠C=n°,则m,n之间的数量关系为 .
14. 如图,AB=6,以 AB 为直径作半圆,弦CD∥AB,将CD上方的图形沿CD向下折叠,使与直径AB恰好相切于点O,则图中阴影部分的面积为 .
15. 如图,AB是⊙O的直径,C是⊙O上的一点,连结AC,BC,AD是⊙O的切线,连结OD.若OD平分AC,∠B=60°,BC=2,则OD= .
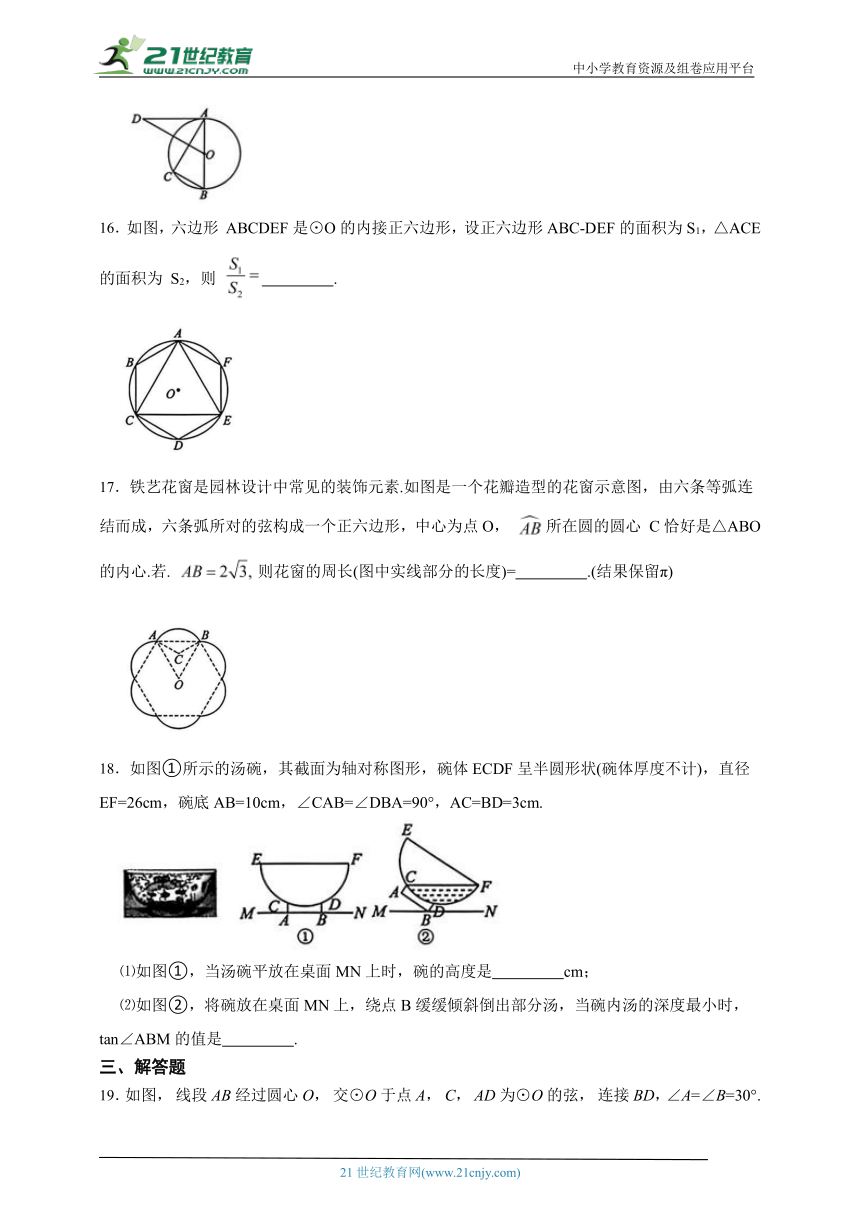
16.如图,六边形 ABCDEF是⊙O的内接正六边形,设正六边形ABC-DEF的面积为S1,△ACE 的面积为 S2,则 .
17.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连结而成,六条弧所对的弦构成一个正六边形,中心为点O, 所在圆的圆心 C恰好是△ABO的内心.若. 则花窗的周长(图中实线部分的长度)= .(结果保留π)
18.如图①所示的汤碗,其截面为轴对称图形,碗体ECDF呈半圆形状(碗体厚度不计),直径EF=26cm,碗底AB=10cm,∠CAB=∠DBA=90°,AC=BD=3cm.
⑴如图①,当汤碗平放在桌面MN上时,碗的高度是 cm;
⑵如图②,将碗放在桌面MN上,绕点B缓缓倾斜倒出部分汤,当碗内汤的深度最小时,tan∠ABM的值是 .
三、解答题
19.如图, 线段AB经过圆心O, 交⊙O于点A, C, AD为⊙O的弦, 连接BD,∠A=∠B=30°.
(1) 求证: 直线 BD是⊙O的切线;
(2) 已知BC=2, 求 的长(结果保留π).
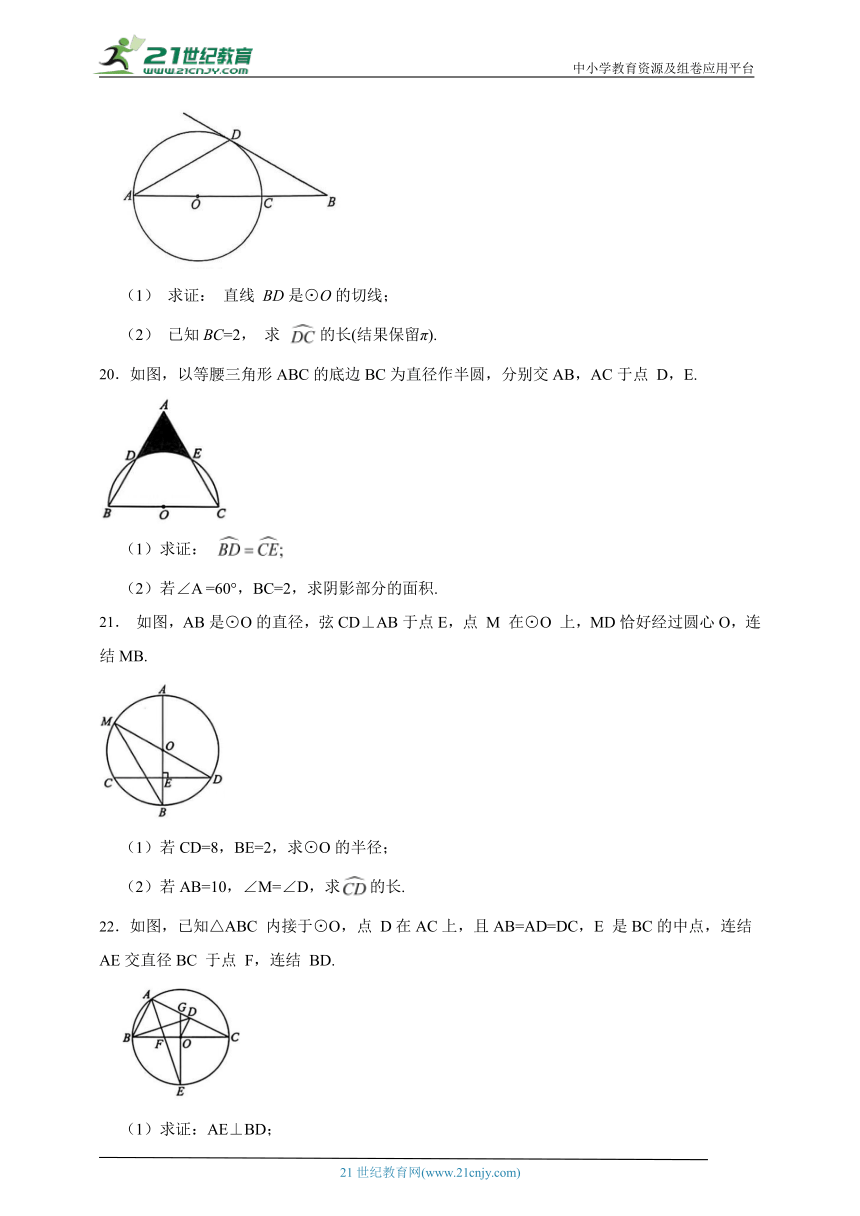
20.如图,以等腰三角形ABC的底边BC为直径作半圆,分别交AB,AC于点 D,E.
(1)求证:
(2)若∠A =60°,BC=2,求阴影部分的面积.
21. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点 M 在⊙O 上,MD恰好经过圆心O,连结MB.
(1)若CD=8,BE=2,求⊙O的半径;
(2)若AB=10,∠M=∠D,求的长.
22.如图,已知△ABC 内接于⊙O,点 D在AC上,且AB=AD=DC,E 是BC的中点,连结AE交直径BC 于点 F,连结 BD.
(1)求证:AE⊥BD;
(2)若 BC=10,求AE的长;
(3)连结 EO 并延长,交 AC 于点 G,连结OD,求 的值.
23. 如图所示,AB 是⊙O的直径,BC,BD 是⊙O的两条弦,点 C 与点 D 在AB的两侧,E 是OB 上一点( 连结 OC,CE,且
(1)如图甲,若 求⊙O的半径;
(2)如图乙,若 求证:
24.在平面直角坐标系xOy中,对于点A和⊙C 给出如下定义:若⊙C上存在两个不同的点M,N,对于⊙C上任意满足AP=AQ的两个不同的点P,Q,都有 则称点A是⊙C的关联点,称∠MAN的大小为点A与⊙C的关联角度.(本定义中的角均指锐角、直角、钝角或平角)
(1)如图,⊙O 的半径为1.
①在点中,点 是⊙O的关联点且其与⊙O的关联角度小于 该点与⊙O 的关联角度为 °;
②点B(1,m)在第一象限,若对于任意长度小于1的线段BD,BD 上所有的点都是⊙O的关联点,则m的最小值为 ;
(2)已知点E(1,3),F(4,3),T(t,0),⊙T经过原点,线段EF上所有的点都是⊙T的关联点,记这些点与⊙T的关联角度的最大值为α.若 直接写出t的取值范围.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】5
13.【答案】m+2n=180
14.【答案】
15.【答案】4
16.【答案】2
17.【答案】8π
18.【答案】15;
19.【答案】(1)证明: 连接OD
∴∠ADB=180°-∠A-∠B=120°
∵OA=OD
∴∠A=∠ODA=30°
∴OD⊥BD
且 OD是⊙O的半径
∴直线BD是⊙O 的切线
(2)在Rt△DOB中, ∠ODB=90°,∠B=30°
设OD=OC=r
解得r=2·
∵∠DOB=∠A+∠ODA=30°+30°=60°或
∵∠DOB=180°-∠ODB-∠B=60°
20.【答案】(1)证明:连结 BE,CD.
∵BC为半圆O的直径,
∴∠BDC=∠CEB=90°.
∵△ABC是等腰三角形,
∴∠DBC=∠ECB.
又∵BC=CB,
∴△DBC≌△ECB(AAS).
∴BD=CE.
(2)解:如图,连接 DO,EO.
∴等腰 为等边三角形,
且
和 为等边三角形,
21.【答案】(1)解:设⊙O的半径为r,
在 中, D
解得
∴⊙O的半径为5;
(2)解:如图, 连接OC,
∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M =2∠B,
∵∠DOE+∠D=90°,
∴2∠B+∠D=90°,
∵∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°,
∴∠DOE=60°,
∴∠COD =120°,
的长为
22.【答案】(1)证明:∵BC是⊙O的直径,
∵E是 的中点,
(2)解:令AE交BD于点P, 连接BE, EC,
∵ BC是⊙O的直径,
∵ E是 的中点,
C,
∵AB= AD, AE⊥BD,
由勾股定理得:
(3)解:∵∠BAC = 90°, AB= AD,
∴△ABD是等腰直角三角形.
∴∠ABD=∠ADB =45°,
∴∠BAE=∠EAC =45°,
∵AD = DC, OD经过圆心,
∴OD⊥AC,
∴∠BDO=∠EAG =45°,
∵AE⊥BD, ∠AFB=∠OFE,
∴∠DBO=∠AEG,
∵∠BDO =∠EAG =45°,
∴△BDO∽△EAG,
设AB=a, 则AC=2a,
在Rt△ABC中,根据勾股定理可得:
在 中,
23.【答案】(1)解:∵OC=OB,∴∠OBC=∠OCB=(180°-∠BOC),
,即
∠OBC+∠BCE=90°,∴∠OEC=90°,∴OC2=OE2+CE2,
解得(OC=3,即⊙O的半径为3.
(2)证明:过O作OF⊥BD于F,
∴BF=BD,∵BD=2OE,
∴BF=OE,又∵OC=OB,BD=2OE,∠OEC=∠BFO=90°,
∴Rt△CEO≌Rt△OFB,∴∠COE=∠OBF,∴BD∥OC
24.【答案】(1)A3;60;
(2)或t>5或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考专项特训】2026年中考数学专项提优练习:圆
一、选择题
1.下列命题正确的是( )
A.三个点确定一个圆
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.同弧或等弧所对的圆周角相等
D.圆内接平行四边形一定是正方形
2. 图1是通过平面图形的镶嵌所呈现的图案,图2是其局部放大示意图,由正六边形、正方形和正三角形构成,它的轮廓为正十二边形,则图2中∠ABC的大小是( )
A.90° B.120° C.135° D.150°
3.如图,某款扫地机器人的俯视图是一个等宽曲边三角形ABC(分别以正△ABC的三个顶点 A,B,C为圆心,AB长为半径画弧得到的图形).若AB=6,则曲边AB的长为( )
A.π B.2π C.6π D.12π
4.如图,点A,B,C在⊙O上,连结OA,OC,AB,AC,BC.若∠B=135°,AC=4,则AC的长为( )
A.π B. C. D.
5. 如图,⊙O是△ABC的外接圆,AB是直径,CD平分∠ACB,AD=2,则⊙O的半径为( )
A.2 B.1 C. D.
6. 如图, AB是⊙O的直径, ∠CAB=40°, 则∠ADC的度数是( )
A.80° B.50° C.40° D.25°
7.《九章算术》是中国古代第一部数学专著,第一章“方田”中已讲述了平面几何图形面积的计算方法,比如扇形面积的计算,“今有宛田,下周三十步,径十六步,问为田几何.”大致意思为:现有一块扇形的田,弧长30步,其所在圆的直径是 16步,则这块田的面积为( )
A.120平方步 B.240平方步
C.平方步 D.π平方步
8.如图,半径为 5 的 扇 形 AOB 中,∠AOB=90°,C 是 上一点,CD⊥OA,CE⊥OB,垂足分别为 D,E.若CD=CE,则图中阴影部分的面积为( )
A. B. C. D.
9.如图所示,将半径为4的圆形纸片折叠使弧AB 经过圆心O,过点O 作直径 于点E,P是半径OD上一动点,连结AP,则AP 的长度不可能是( )
A.4 B.5 C.6 D.7
10. 如图所示,在矩形纸片 ABCD 中,AD=6cm,把它分割成正方形纸片ABFE 和矩形纸片EFCD 后,分别裁出扇形 ABF 和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为( )
A.3. 5cm B.4cm C.4. 5cm D.5cm
二、填空题
11.如图,圆锥的底面半径为3,高为4,则该圆锥的侧面积为 .
12. 如图,AB是⊙O的切线,B为切点,作AC⊥AB交AB于点A,AC交⊙O于C,D两点.若AB=3,AC=9,则⊙O的半径是
13.如图,过⊙O外一点P作圆的切线PA,PB,A,B为切点,AC为⊙O的直径,设∠P=m°,∠C=n°,则m,n之间的数量关系为 .
14. 如图,AB=6,以 AB 为直径作半圆,弦CD∥AB,将CD上方的图形沿CD向下折叠,使与直径AB恰好相切于点O,则图中阴影部分的面积为 .
15. 如图,AB是⊙O的直径,C是⊙O上的一点,连结AC,BC,AD是⊙O的切线,连结OD.若OD平分AC,∠B=60°,BC=2,则OD= .
16.如图,六边形 ABCDEF是⊙O的内接正六边形,设正六边形ABC-DEF的面积为S1,△ACE 的面积为 S2,则 .
17.铁艺花窗是园林设计中常见的装饰元素.如图是一个花瓣造型的花窗示意图,由六条等弧连结而成,六条弧所对的弦构成一个正六边形,中心为点O, 所在圆的圆心 C恰好是△ABO的内心.若. 则花窗的周长(图中实线部分的长度)= .(结果保留π)
18.如图①所示的汤碗,其截面为轴对称图形,碗体ECDF呈半圆形状(碗体厚度不计),直径EF=26cm,碗底AB=10cm,∠CAB=∠DBA=90°,AC=BD=3cm.
⑴如图①,当汤碗平放在桌面MN上时,碗的高度是 cm;
⑵如图②,将碗放在桌面MN上,绕点B缓缓倾斜倒出部分汤,当碗内汤的深度最小时,tan∠ABM的值是 .
三、解答题
19.如图, 线段AB经过圆心O, 交⊙O于点A, C, AD为⊙O的弦, 连接BD,∠A=∠B=30°.
(1) 求证: 直线 BD是⊙O的切线;
(2) 已知BC=2, 求 的长(结果保留π).
20.如图,以等腰三角形ABC的底边BC为直径作半圆,分别交AB,AC于点 D,E.
(1)求证:
(2)若∠A =60°,BC=2,求阴影部分的面积.
21. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点 M 在⊙O 上,MD恰好经过圆心O,连结MB.
(1)若CD=8,BE=2,求⊙O的半径;
(2)若AB=10,∠M=∠D,求的长.
22.如图,已知△ABC 内接于⊙O,点 D在AC上,且AB=AD=DC,E 是BC的中点,连结AE交直径BC 于点 F,连结 BD.
(1)求证:AE⊥BD;
(2)若 BC=10,求AE的长;
(3)连结 EO 并延长,交 AC 于点 G,连结OD,求 的值.
23. 如图所示,AB 是⊙O的直径,BC,BD 是⊙O的两条弦,点 C 与点 D 在AB的两侧,E 是OB 上一点( 连结 OC,CE,且
(1)如图甲,若 求⊙O的半径;
(2)如图乙,若 求证:
24.在平面直角坐标系xOy中,对于点A和⊙C 给出如下定义:若⊙C上存在两个不同的点M,N,对于⊙C上任意满足AP=AQ的两个不同的点P,Q,都有 则称点A是⊙C的关联点,称∠MAN的大小为点A与⊙C的关联角度.(本定义中的角均指锐角、直角、钝角或平角)
(1)如图,⊙O 的半径为1.
①在点中,点 是⊙O的关联点且其与⊙O的关联角度小于 该点与⊙O 的关联角度为 °;
②点B(1,m)在第一象限,若对于任意长度小于1的线段BD,BD 上所有的点都是⊙O的关联点,则m的最小值为 ;
(2)已知点E(1,3),F(4,3),T(t,0),⊙T经过原点,线段EF上所有的点都是⊙T的关联点,记这些点与⊙T的关联角度的最大值为α.若 直接写出t的取值范围.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】B
11.【答案】
12.【答案】5
13.【答案】m+2n=180
14.【答案】
15.【答案】4
16.【答案】2
17.【答案】8π
18.【答案】15;
19.【答案】(1)证明: 连接OD
∴∠ADB=180°-∠A-∠B=120°
∵OA=OD
∴∠A=∠ODA=30°
∴OD⊥BD
且 OD是⊙O的半径
∴直线BD是⊙O 的切线
(2)在Rt△DOB中, ∠ODB=90°,∠B=30°
设OD=OC=r
解得r=2·
∵∠DOB=∠A+∠ODA=30°+30°=60°或
∵∠DOB=180°-∠ODB-∠B=60°
20.【答案】(1)证明:连结 BE,CD.
∵BC为半圆O的直径,
∴∠BDC=∠CEB=90°.
∵△ABC是等腰三角形,
∴∠DBC=∠ECB.
又∵BC=CB,
∴△DBC≌△ECB(AAS).
∴BD=CE.
(2)解:如图,连接 DO,EO.
∴等腰 为等边三角形,
且
和 为等边三角形,
21.【答案】(1)解:设⊙O的半径为r,
在 中, D
解得
∴⊙O的半径为5;
(2)解:如图, 连接OC,
∵OM=OB,
∴∠B=∠M,
∴∠DOB=∠B+∠M =2∠B,
∵∠DOE+∠D=90°,
∴2∠B+∠D=90°,
∵∠B=∠D,
∴2∠D+∠D=90°,
∴∠D=30°,
∴∠DOE=60°,
∴∠COD =120°,
的长为
22.【答案】(1)证明:∵BC是⊙O的直径,
∵E是 的中点,
(2)解:令AE交BD于点P, 连接BE, EC,
∵ BC是⊙O的直径,
∵ E是 的中点,
C,
∵AB= AD, AE⊥BD,
由勾股定理得:
(3)解:∵∠BAC = 90°, AB= AD,
∴△ABD是等腰直角三角形.
∴∠ABD=∠ADB =45°,
∴∠BAE=∠EAC =45°,
∵AD = DC, OD经过圆心,
∴OD⊥AC,
∴∠BDO=∠EAG =45°,
∵AE⊥BD, ∠AFB=∠OFE,
∴∠DBO=∠AEG,
∵∠BDO =∠EAG =45°,
∴△BDO∽△EAG,
设AB=a, 则AC=2a,
在Rt△ABC中,根据勾股定理可得:
在 中,
23.【答案】(1)解:∵OC=OB,∴∠OBC=∠OCB=(180°-∠BOC),
,即
∠OBC+∠BCE=90°,∴∠OEC=90°,∴OC2=OE2+CE2,
解得(OC=3,即⊙O的半径为3.
(2)证明:过O作OF⊥BD于F,
∴BF=BD,∵BD=2OE,
∴BF=OE,又∵OC=OB,BD=2OE,∠OEC=∠BFO=90°,
∴Rt△CEO≌Rt△OFB,∴∠COE=∠OBF,∴BD∥OC
24.【答案】(1)A3;60;
(2)或t>5或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
