【中考专项特训】2026年中考数学专项提优练习:一次函数(含答案)
文档属性
| 名称 | 【中考专项特训】2026年中考数学专项提优练习:一次函数(含答案) | 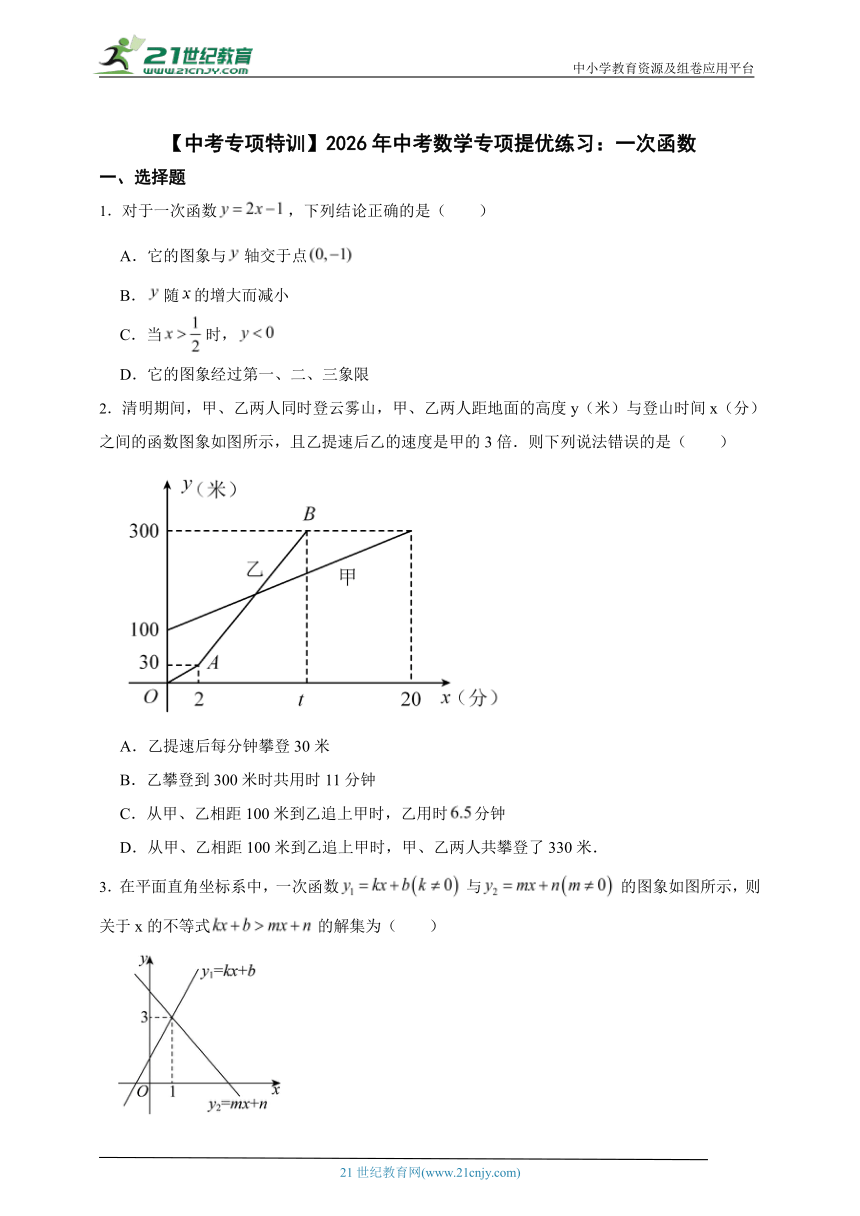 | |
| 格式 | docx | ||
| 文件大小 | 734.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 14:10:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【中考专项特训】2026年中考数学专项提优练习:一次函数
一、选择题
1.对于一次函数,下列结论正确的是( )
A.它的图象与轴交于点
B.随的增大而减小
C.当时,
D.它的图象经过第一、二、三象限
2.清明期间,甲、乙两人同时登云雾山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,且乙提速后乙的速度是甲的3倍.则下列说法错误的是( )
A.乙提速后每分钟攀登30米
B.乙攀登到300米时共用时11分钟
C.从甲、乙相距100米到乙追上甲时,乙用时分钟
D.从甲、乙相距100米到乙追上甲时,甲、乙两人共攀登了330米.
3.在平面直角坐标系中,一次函数与的图象如图所示,则关于x的不等式的解集为( )
A. B. C. D.
4.一次函数的图象如图所示,则点在第( )象限
A.一 B.二 C.三 D.四
5.若反比例函数经过点,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在“探索一次函数的系数k,b与图象的关系”活动中,老师给出了坐标系中的三个点:,如图所示,同学们画出了经过这三个点中每两个点的一次函数图象,并得到对应的函数表达式为:.分别计算的值,其中最大的值是( ).
A. B. C.5 D.3
7.某吊绳最大承受拉力对应的重物质量不超过8 吨.当没有吊起任何重物时,吊绳的自然长度是5米,通过实验测定,每吊起1 吨重物,吊绳会伸长0.3米.在吊绳的弹性限度内,吊起重物后吊绳的长度y(单位:米)与所吊重物的质量x(单位:吨)之间的函数关系式为( )
A. B.
C. D.
8.定义:若x,y满足,(m为常数),则称为“和谐点”.下列说法正确的是( )
①是“和谐点”;②直线上有且只有一个“和谐点”;③当时,反比例函数的图象上最多只有两个“和谐点”;④若二次函数的图象上有3个“和谐点”,则或.
A.①③ B.①④ C.②③ D.②④
9.如图,正比函数的图象与一次函数的图象相交于点,则方程组的解是( )
A. B. C. D.
10.如图,入射光线遇到平面镜(轴)上的点后,反射光线交轴于点,若光线满足的一次函数关系式为,则的值是( )
A. B. C. D.
二、填空题
11.若一次函数 的图像与 轴交于点 ,则 .
12.若点和是一次函数的图象上两点,则与的大小关系为: (填“”,“”或“”).
13.如图,在平面直角坐标系中,点A是x轴上一动点,点B是直线上一动点,,,则的最大值是 .
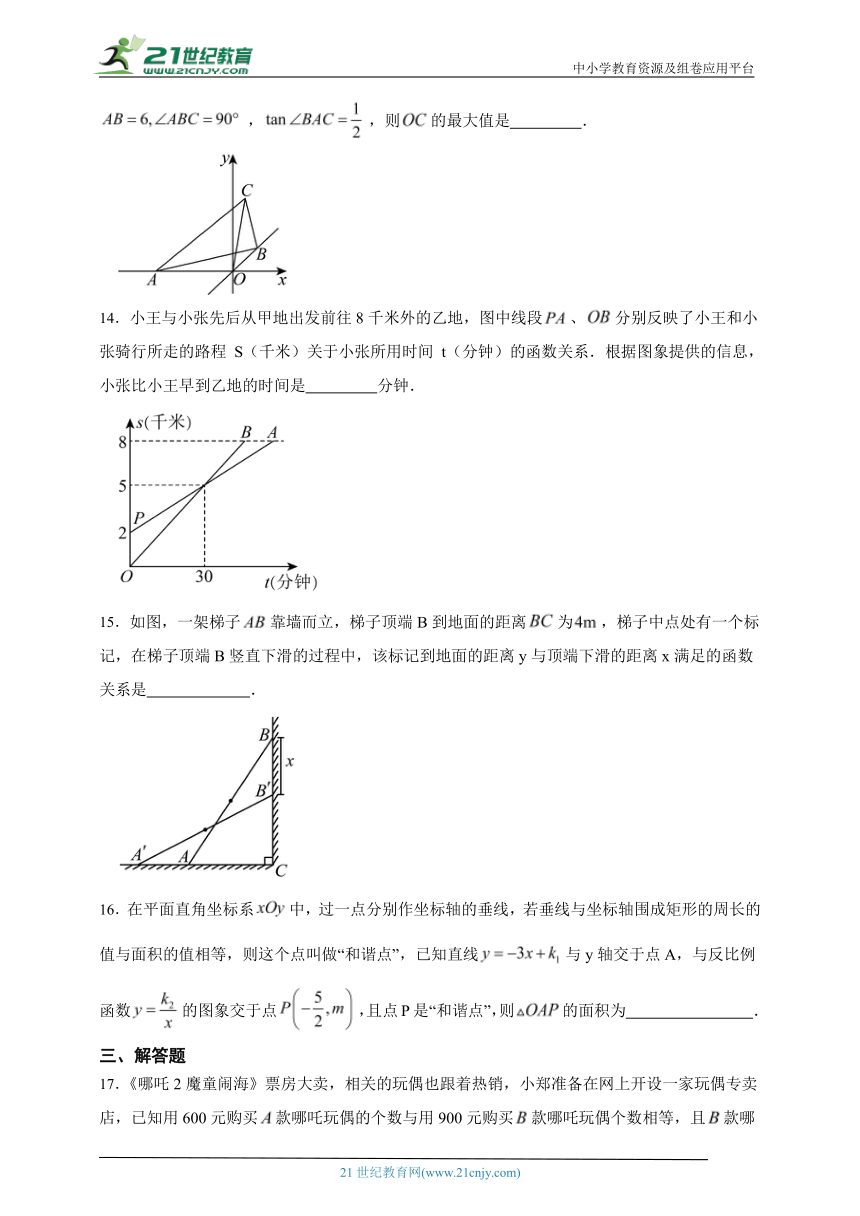
14.小王与小张先后从甲地出发前往8千米外的乙地,图中线段、分别反映了小王和小张骑行所走的路程 S(千米)关于小张所用时间 t(分钟)的函数关系.根据图象提供的信息,小张比小王早到乙地的时间是 分钟.
15.如图,一架梯子靠墙而立,梯子顶端B到地面的距离为,梯子中点处有一个标记,在梯子顶端B竖直下滑的过程中,该标记到地面的距离y与顶端下滑的距离x满足的函数关系是 .
16.在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的值与面积的值相等,则这个点叫做“和谐点”,已知直线与y轴交于点A,与反比例函数的图象交于点,且点P是“和谐点”,则的面积为 .
三、解答题
17.《哪吒2魔童闹海》票房大卖,相关的玩偶也跟着热销,小郑准备在网上开设一家玩偶专卖店,已知用600元购买款哪吒玩偶的个数与用900元购买款哪吒玩偶个数相等,且款哪吒玩偶单价比款哪吒玩偶单价多3元.
(1),款哪吒玩偶每个各多少元?
(2)试营业时计划购买款哪吒玩偶共200个,其中款哪吒玩偶的数量不超过款哪吒玩偶数量的,求购买款哪吒玩偶多少个时,购买这批玩偶总费用最低,最低费用是多少元?
18.如图,在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处保持的速度匀速运动小聪测量黑球减速后运动距离单位:随运动时间单位:变化的数据,整理得下表.
运动时间
运动距离
探究发现,与之间的数量关系可以用二次函数来描述.
(1)求关于的函数关系式.
(2)当时,求两球之间的距离.
(3)黑球能否追上白球?若能,求出追上时的值;若不能,求出它们之间的最短距离.
19.2025年是全面落实全国科技大会精神、加快建设科技强国的关键之年,人工智能的崛起无疑成为了全球科技界的焦点.某公司尝试利用智能技术优化生产流程,提高生产效率.在生产一种产品时,发现生产成本y(单位:元)与产品数量x(单位:件)之间存在一次函数关系,其几组对应值如下表所示.
产品数量x/件 … 10 12 16 20 …
生产成本y/元 … 400 420 460 500 …
请你根据表中信息,解答下列问题.
(1)求y与x之间的函数关系式.
(2)若这种产品每件的售价为20元,则当生产成本为1000元时,所生产产品的总售价为多少元?
20.小明和小白两人从同一地方出发,分别自驾前往外的景点游玩,小明与小白在服务区均休息了一次,每人每次休息30分钟.行驶过程中,两人的速度始终保持不变,具体时间与路程信息如图所示.
(1)求两人的行驶速度.
(2)求小白休息后的(段)行驶路程关于时间的函数.
(3)求小明追上小白时的时间.
21.如图,在平面直角坐标系中,点在直线上,矩形的顶点,在坐标轴上,,点在上运动.
(1)如图(1),当时,求点的坐标;
(2)如图(2),连接,将绕点顺时针旋转得到,若,求点坐标;
(3)如图(3),点在上,垂直平分交于点,当时,求的值.
22.某数学兴趣小组进行项目式学习成果的展示,他们利用“杠杆原理”制作出一种投石机,如图,为检验投石机的性能,进行如下操作:将石头用投石机从处投出,石头的运动轨迹是抛物线的一部分,最终石头落在斜坡上的点C处,以水平地面为轴,为轴建立平面直角坐标系如图.已知抛物线的函数表达式为,直线的函数表达式为,米,点为抛物线的顶点,过点作轴于点,点到轴的水平距离米.
(1)请求出抛物线的函数表达式;
(2)求点的坐标.
(3)点是点左侧抛物线上一点,过点作轴交坡面于点,若石头运动到点时到坡面的铅直高度为米,求此时石头(点)到轴的距离.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】2
12.【答案】
13.【答案】
14.【答案】12
15.【答案】
16.【答案】或
17.【答案】(1)、款哪吒玩偶每个各6元和9元
(2)购买款哪吒玩偶50个时,购买这批哪吒玩偶总费用最低,最低费用是1650元
18.【答案】(1)解:设关于的函数解析式为将点,,得:
,
解得,
关于的函数解析式为;
(2)解:令表示两球之间的距离由题意可得,
,
当时,,
答:两球之间的距离为;
(3)解:,
,
当时,有最短距离为.
两球不能相遇,它们之间的最短距离为.
19.【答案】(1)
(2)当生产成本为1000元时,所生产的产品总售价为1400元
20.【答案】(1)解:30分钟=0.5小时,
小明的行驶速度为:,
小白的行驶速度为:.
(2)解:由题意可得:1+0.5=1.5,
∴点A的坐标为(1.5,80),
设小白休息后的(段)行驶路程关于时间x的函数解析式为y=80x+b,
∴80=80×1.5+b,
解得:b=-40,
∴小白休息后的(段)行驶路程关于时间x的函数解析式为y=80x-40.
(3)解:设小白休息后的行驶路程关于时间x的函数解析式为y=100x+m,
将(2.2,120)代入y=100x+m,得:120=100×2.2+m,
解得:m=-100,
∴y=100x-100,
由题意可得:80x-40=100x-100,
解得:x=3,
∴ 小明追上小白时的时间a=3.
21.【答案】(1)
(2)
(3)
22.【答案】(1);
(2);
(3)石头到轴的距离为米
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考专项特训】2026年中考数学专项提优练习:一次函数
一、选择题
1.对于一次函数,下列结论正确的是( )
A.它的图象与轴交于点
B.随的增大而减小
C.当时,
D.它的图象经过第一、二、三象限
2.清明期间,甲、乙两人同时登云雾山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,且乙提速后乙的速度是甲的3倍.则下列说法错误的是( )
A.乙提速后每分钟攀登30米
B.乙攀登到300米时共用时11分钟
C.从甲、乙相距100米到乙追上甲时,乙用时分钟
D.从甲、乙相距100米到乙追上甲时,甲、乙两人共攀登了330米.
3.在平面直角坐标系中,一次函数与的图象如图所示,则关于x的不等式的解集为( )
A. B. C. D.
4.一次函数的图象如图所示,则点在第( )象限
A.一 B.二 C.三 D.四
5.若反比例函数经过点,则一次函数的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.在“探索一次函数的系数k,b与图象的关系”活动中,老师给出了坐标系中的三个点:,如图所示,同学们画出了经过这三个点中每两个点的一次函数图象,并得到对应的函数表达式为:.分别计算的值,其中最大的值是( ).
A. B. C.5 D.3
7.某吊绳最大承受拉力对应的重物质量不超过8 吨.当没有吊起任何重物时,吊绳的自然长度是5米,通过实验测定,每吊起1 吨重物,吊绳会伸长0.3米.在吊绳的弹性限度内,吊起重物后吊绳的长度y(单位:米)与所吊重物的质量x(单位:吨)之间的函数关系式为( )
A. B.
C. D.
8.定义:若x,y满足,(m为常数),则称为“和谐点”.下列说法正确的是( )
①是“和谐点”;②直线上有且只有一个“和谐点”;③当时,反比例函数的图象上最多只有两个“和谐点”;④若二次函数的图象上有3个“和谐点”,则或.
A.①③ B.①④ C.②③ D.②④
9.如图,正比函数的图象与一次函数的图象相交于点,则方程组的解是( )
A. B. C. D.
10.如图,入射光线遇到平面镜(轴)上的点后,反射光线交轴于点,若光线满足的一次函数关系式为,则的值是( )
A. B. C. D.
二、填空题
11.若一次函数 的图像与 轴交于点 ,则 .
12.若点和是一次函数的图象上两点,则与的大小关系为: (填“”,“”或“”).
13.如图,在平面直角坐标系中,点A是x轴上一动点,点B是直线上一动点,,,则的最大值是 .
14.小王与小张先后从甲地出发前往8千米外的乙地,图中线段、分别反映了小王和小张骑行所走的路程 S(千米)关于小张所用时间 t(分钟)的函数关系.根据图象提供的信息,小张比小王早到乙地的时间是 分钟.
15.如图,一架梯子靠墙而立,梯子顶端B到地面的距离为,梯子中点处有一个标记,在梯子顶端B竖直下滑的过程中,该标记到地面的距离y与顶端下滑的距离x满足的函数关系是 .
16.在平面直角坐标系中,过一点分别作坐标轴的垂线,若垂线与坐标轴围成矩形的周长的值与面积的值相等,则这个点叫做“和谐点”,已知直线与y轴交于点A,与反比例函数的图象交于点,且点P是“和谐点”,则的面积为 .
三、解答题
17.《哪吒2魔童闹海》票房大卖,相关的玩偶也跟着热销,小郑准备在网上开设一家玩偶专卖店,已知用600元购买款哪吒玩偶的个数与用900元购买款哪吒玩偶个数相等,且款哪吒玩偶单价比款哪吒玩偶单价多3元.
(1),款哪吒玩偶每个各多少元?
(2)试营业时计划购买款哪吒玩偶共200个,其中款哪吒玩偶的数量不超过款哪吒玩偶数量的,求购买款哪吒玩偶多少个时,购买这批玩偶总费用最低,最低费用是多少元?
18.如图,在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处保持的速度匀速运动小聪测量黑球减速后运动距离单位:随运动时间单位:变化的数据,整理得下表.
运动时间
运动距离
探究发现,与之间的数量关系可以用二次函数来描述.
(1)求关于的函数关系式.
(2)当时,求两球之间的距离.
(3)黑球能否追上白球?若能,求出追上时的值;若不能,求出它们之间的最短距离.
19.2025年是全面落实全国科技大会精神、加快建设科技强国的关键之年,人工智能的崛起无疑成为了全球科技界的焦点.某公司尝试利用智能技术优化生产流程,提高生产效率.在生产一种产品时,发现生产成本y(单位:元)与产品数量x(单位:件)之间存在一次函数关系,其几组对应值如下表所示.
产品数量x/件 … 10 12 16 20 …
生产成本y/元 … 400 420 460 500 …
请你根据表中信息,解答下列问题.
(1)求y与x之间的函数关系式.
(2)若这种产品每件的售价为20元,则当生产成本为1000元时,所生产产品的总售价为多少元?
20.小明和小白两人从同一地方出发,分别自驾前往外的景点游玩,小明与小白在服务区均休息了一次,每人每次休息30分钟.行驶过程中,两人的速度始终保持不变,具体时间与路程信息如图所示.
(1)求两人的行驶速度.
(2)求小白休息后的(段)行驶路程关于时间的函数.
(3)求小明追上小白时的时间.
21.如图,在平面直角坐标系中,点在直线上,矩形的顶点,在坐标轴上,,点在上运动.
(1)如图(1),当时,求点的坐标;
(2)如图(2),连接,将绕点顺时针旋转得到,若,求点坐标;
(3)如图(3),点在上,垂直平分交于点,当时,求的值.
22.某数学兴趣小组进行项目式学习成果的展示,他们利用“杠杆原理”制作出一种投石机,如图,为检验投石机的性能,进行如下操作:将石头用投石机从处投出,石头的运动轨迹是抛物线的一部分,最终石头落在斜坡上的点C处,以水平地面为轴,为轴建立平面直角坐标系如图.已知抛物线的函数表达式为,直线的函数表达式为,米,点为抛物线的顶点,过点作轴于点,点到轴的水平距离米.
(1)请求出抛物线的函数表达式;
(2)求点的坐标.
(3)点是点左侧抛物线上一点,过点作轴交坡面于点,若石头运动到点时到坡面的铅直高度为米,求此时石头(点)到轴的距离.
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】2
12.【答案】
13.【答案】
14.【答案】12
15.【答案】
16.【答案】或
17.【答案】(1)、款哪吒玩偶每个各6元和9元
(2)购买款哪吒玩偶50个时,购买这批哪吒玩偶总费用最低,最低费用是1650元
18.【答案】(1)解:设关于的函数解析式为将点,,得:
,
解得,
关于的函数解析式为;
(2)解:令表示两球之间的距离由题意可得,
,
当时,,
答:两球之间的距离为;
(3)解:,
,
当时,有最短距离为.
两球不能相遇,它们之间的最短距离为.
19.【答案】(1)
(2)当生产成本为1000元时,所生产的产品总售价为1400元
20.【答案】(1)解:30分钟=0.5小时,
小明的行驶速度为:,
小白的行驶速度为:.
(2)解:由题意可得:1+0.5=1.5,
∴点A的坐标为(1.5,80),
设小白休息后的(段)行驶路程关于时间x的函数解析式为y=80x+b,
∴80=80×1.5+b,
解得:b=-40,
∴小白休息后的(段)行驶路程关于时间x的函数解析式为y=80x-40.
(3)解:设小白休息后的行驶路程关于时间x的函数解析式为y=100x+m,
将(2.2,120)代入y=100x+m,得:120=100×2.2+m,
解得:m=-100,
∴y=100x-100,
由题意可得:80x-40=100x-100,
解得:x=3,
∴ 小明追上小白时的时间a=3.
21.【答案】(1)
(2)
(3)
22.【答案】(1);
(2);
(3)石头到轴的距离为米
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
