【中考专项特训】2026年中考数学专项提优练习:三角形(含答案)
文档属性
| 名称 | 【中考专项特训】2026年中考数学专项提优练习:三角形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 934.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 14:09:46 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【中考专项特训】2026年中考数学专项提优练习:三角形
一、选择题
1.如图,在的正方形网格中,线段AB,CD的端点均在格点上,则和的数量关系是( )
A. B.
C. D.
2.尺规作图:过直线AB外一点P作直线AB的平行线,下列作法错误的是( ).
A. B.
C. D.
3.如图,某仓库正门的截面是一个半径为的半圆,一辆高为的矩形货车恰好能通过该仓库正门.则车宽为( )
A. B. C. D.
4.如图,在矩形中,为边上一点,,将沿折叠得,连接,若平分,,则的长为( )
A. B. C. D.
5.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,,若以点A为圆心,的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为( )
A. B. C. D.
6.如图所示,在中,,以其三边为边向外作正方形作≌,且,达芬奇通过四边形旋转与四边形重合的思路证明了勾股定理若,四边形的面积则的长是( )
A. B. C. D.
7.如图,正方形的对角线上有一点E,且,点F在的延长线上,连接,过点E作,交的延长线于点G,连接并延长,交的延长线于点P,若,,求线段的长( ).
A. B. C. D.
8.如图,在的正方形方格中,的顶点,都在边长为的小正方形的顶点上,边上的点也在小正方形的顶点上,则的面积等于( )
A. B. C. D.
9.赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形ABCD,中间是一个小正方形EFGH,连接DE与FG相交于点M,延长DE交BC于点N,若M是DE的中点,,则EN的长( )
A. B. C.2 D.
二、填空题
10.如图,在中,,,,用图示的尺规作图方法在边上确定一点.则的周长为 .
11.如图,,,,则 .
12.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= 。
13.如图,一把直尺的边缘经过一块三角板的直角顶点,交斜边于点,直尺的边缘分别交,于点,,若,,则的度数为 度.
14.如图,在中,是上一点,连接,,过作于点,交于点,且,若,,则的长为 .
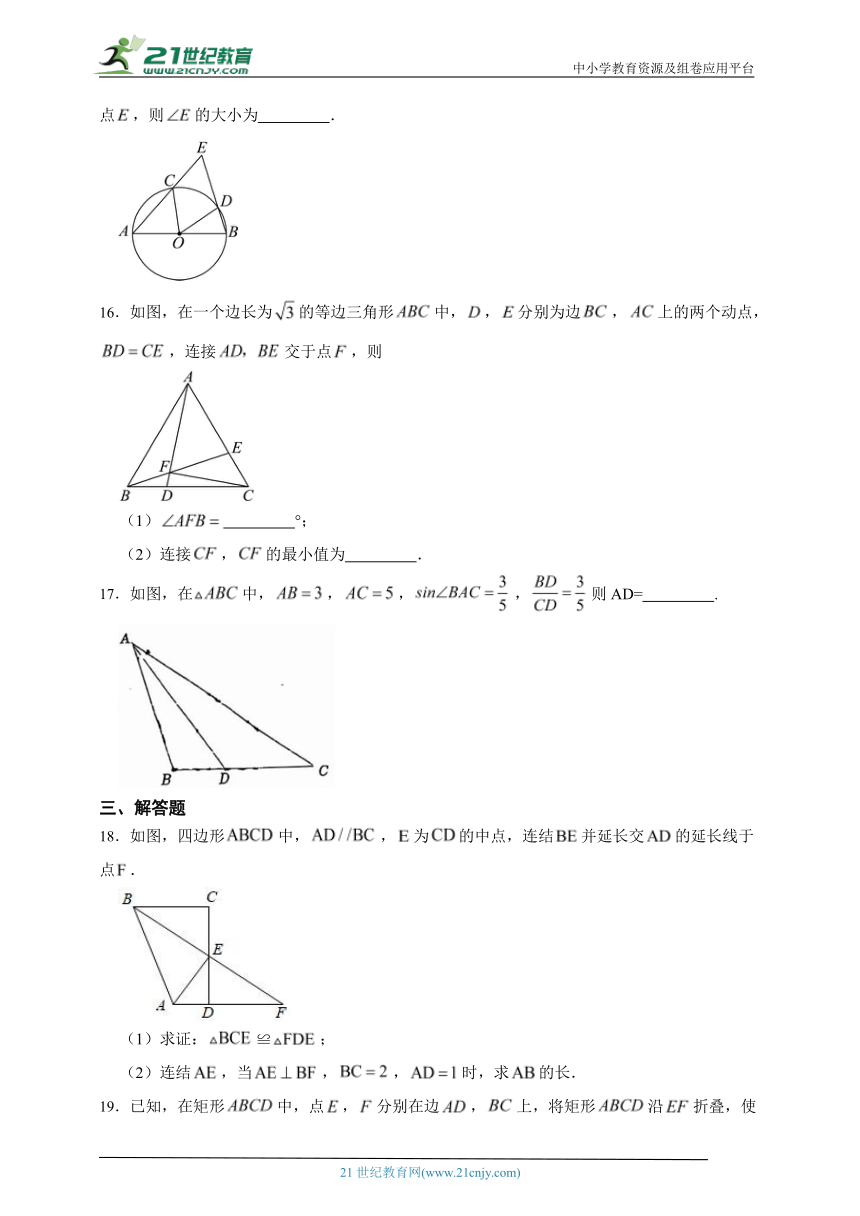
15.如图,为的直径,、为圆上两点且,连接、并延长交于点,则的大小为 .
16.如图,在一个边长为的等边三角形中,,分别为边,上的两个动点,,连接交于点,则
(1) °;
(2)连接,的最小值为 .
17.如图,在中,,,,则AD= .
三、解答题
18.如图,四边形中,,为的中点,连结并延长交的延长线于点.
(1)求证:≌;
(2)连结,当,,时,求的长.
19.已知,在矩形中,点,分别在边,上,将矩形沿折叠,使点的对应点落在边的中点上,交于点,连接.
(1)如图,若,时
①_____
②求的长;
(2)若为的三等分点,求的值.
20.如图,四边形为矩形,点在轴正半轴上,点在轴正半轴上,点的坐标为,反比例函数的图像与边,分别交于点,(不与边的端点重合),连接,,.
(1)若为边的中点,求的值及点的坐标;
(2)若,求的面积.
21.如图,点在同一条直线上,分别是与的平分线,.
(1)求证:四边形是矩形;
(2)若,矩形的面积为,求内切圆的半径.
22.【问题情境】
如图1,在中,,,,是斜边的中线.
【操作判断】
(1)如图,将沿方向平移,当点落在点的位置时,点,的对应点分别是点,,连接,.则线段与的数量关系是:__________.
【深入思考】
将绕点顺时针旋转得到,,的对应点分别是,.
(2)如图,当时,垂足为,与交于点,与交于点,求线段的长.
(3)在旋转的过程中,线段与交于点,当点在线段上时,试求线段的长.
23.综合与实践
图1是某高铁二等座小桌板,它的设计需兼顾空间利用、结构稳定与乘客安全.图2是小桌板展开后的侧面示意图,其中为支架,为桌面的宽,调节椅背不会改变与的位置,与地面保持平行且.当椅背垂直于地面时,与的夹角为.
(,,,,,)
(1)求的度数;
(2)为保证小桌板结构稳定,支架能承受的最大力F为,F与满足,其中m是物体的质量,.求小桌板能放置物体的最大质量;
(3)图3是一圆柱形水杯放置于小桌板上的俯视图,底面圆心为点Q,点Q到的距离为;图4是此时小桌板的侧面示意图,水杯半径,支架,当椅背向后调节至处时,在水杯不被碰倒的情况下,其最大高度是多少?
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】A
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】A
9.【答案】C
10.【答案】15
11.【答案】72
12.【答案】180°
13.【答案】
14.【答案】
15.【答案】
16.【答案】;1
17.【答案】
18.【答案】(1)证明:,
,,
点为的中点,
,
在和中,
,
≌;
(2)解:≌,
,,
,
,
,
的长为.
19.【答案】(1)①,②
(2)或1
20.【答案】(1), 点E坐标为
(2)15
21.【答案】(1)证明:分别是与的平分线,
,,
,
,即,
,
,
四边形是矩形;
(2)解:如图,设的内切圆半径为,,
圆为的内切圆,切点分别为、、,连接,连接,
则,,.
,
,即,
,,
矩形的面积为,
的面积为,
,,
即,,
负值已舍,,
内切圆的半径为.
22.【答案】(1);(2);(3)或
23.【答案】(1)
(2)
(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【中考专项特训】2026年中考数学专项提优练习:三角形
一、选择题
1.如图,在的正方形网格中,线段AB,CD的端点均在格点上,则和的数量关系是( )
A. B.
C. D.
2.尺规作图:过直线AB外一点P作直线AB的平行线,下列作法错误的是( ).
A. B.
C. D.
3.如图,某仓库正门的截面是一个半径为的半圆,一辆高为的矩形货车恰好能通过该仓库正门.则车宽为( )
A. B. C. D.
4.如图,在矩形中,为边上一点,,将沿折叠得,连接,若平分,,则的长为( )
A. B. C. D.
5.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,,若以点A为圆心,的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为( )
A. B. C. D.
6.如图所示,在中,,以其三边为边向外作正方形作≌,且,达芬奇通过四边形旋转与四边形重合的思路证明了勾股定理若,四边形的面积则的长是( )
A. B. C. D.
7.如图,正方形的对角线上有一点E,且,点F在的延长线上,连接,过点E作,交的延长线于点G,连接并延长,交的延长线于点P,若,,求线段的长( ).
A. B. C. D.
8.如图,在的正方形方格中,的顶点,都在边长为的小正方形的顶点上,边上的点也在小正方形的顶点上,则的面积等于( )
A. B. C. D.
9.赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形ABCD,中间是一个小正方形EFGH,连接DE与FG相交于点M,延长DE交BC于点N,若M是DE的中点,,则EN的长( )
A. B. C.2 D.
二、填空题
10.如图,在中,,,,用图示的尺规作图方法在边上确定一点.则的周长为 .
11.如图,,,,则 .
12.如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4= 。
13.如图,一把直尺的边缘经过一块三角板的直角顶点,交斜边于点,直尺的边缘分别交,于点,,若,,则的度数为 度.
14.如图,在中,是上一点,连接,,过作于点,交于点,且,若,,则的长为 .
15.如图,为的直径,、为圆上两点且,连接、并延长交于点,则的大小为 .
16.如图,在一个边长为的等边三角形中,,分别为边,上的两个动点,,连接交于点,则
(1) °;
(2)连接,的最小值为 .
17.如图,在中,,,,则AD= .
三、解答题
18.如图,四边形中,,为的中点,连结并延长交的延长线于点.
(1)求证:≌;
(2)连结,当,,时,求的长.
19.已知,在矩形中,点,分别在边,上,将矩形沿折叠,使点的对应点落在边的中点上,交于点,连接.
(1)如图,若,时
①_____
②求的长;
(2)若为的三等分点,求的值.
20.如图,四边形为矩形,点在轴正半轴上,点在轴正半轴上,点的坐标为,反比例函数的图像与边,分别交于点,(不与边的端点重合),连接,,.
(1)若为边的中点,求的值及点的坐标;
(2)若,求的面积.
21.如图,点在同一条直线上,分别是与的平分线,.
(1)求证:四边形是矩形;
(2)若,矩形的面积为,求内切圆的半径.
22.【问题情境】
如图1,在中,,,,是斜边的中线.
【操作判断】
(1)如图,将沿方向平移,当点落在点的位置时,点,的对应点分别是点,,连接,.则线段与的数量关系是:__________.
【深入思考】
将绕点顺时针旋转得到,,的对应点分别是,.
(2)如图,当时,垂足为,与交于点,与交于点,求线段的长.
(3)在旋转的过程中,线段与交于点,当点在线段上时,试求线段的长.
23.综合与实践
图1是某高铁二等座小桌板,它的设计需兼顾空间利用、结构稳定与乘客安全.图2是小桌板展开后的侧面示意图,其中为支架,为桌面的宽,调节椅背不会改变与的位置,与地面保持平行且.当椅背垂直于地面时,与的夹角为.
(,,,,,)
(1)求的度数;
(2)为保证小桌板结构稳定,支架能承受的最大力F为,F与满足,其中m是物体的质量,.求小桌板能放置物体的最大质量;
(3)图3是一圆柱形水杯放置于小桌板上的俯视图,底面圆心为点Q,点Q到的距离为;图4是此时小桌板的侧面示意图,水杯半径,支架,当椅背向后调节至处时,在水杯不被碰倒的情况下,其最大高度是多少?
答案解析部分
1.【答案】A
2.【答案】D
3.【答案】A
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】A
9.【答案】C
10.【答案】15
11.【答案】72
12.【答案】180°
13.【答案】
14.【答案】
15.【答案】
16.【答案】;1
17.【答案】
18.【答案】(1)证明:,
,,
点为的中点,
,
在和中,
,
≌;
(2)解:≌,
,,
,
,
,
的长为.
19.【答案】(1)①,②
(2)或1
20.【答案】(1), 点E坐标为
(2)15
21.【答案】(1)证明:分别是与的平分线,
,,
,
,即,
,
,
四边形是矩形;
(2)解:如图,设的内切圆半径为,,
圆为的内切圆,切点分别为、、,连接,连接,
则,,.
,
,即,
,,
矩形的面积为,
的面积为,
,,
即,,
负值已舍,,
内切圆的半径为.
22.【答案】(1);(2);(3)或
23.【答案】(1)
(2)
(3)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
