24.2.2 垂直于弦的直径 课件(共22张PPT) 沪科版数学九年级下册
文档属性
| 名称 | 24.2.2 垂直于弦的直径 课件(共22张PPT) 沪科版数学九年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 931.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
11.2三角形全等的判定 (ASA)(AAS)
24.2.2垂径定理
垂径定理
定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所
对的两条弧。
课堂讨论
根据已知条件进行推导:
①过圆心
②垂直于弦
③平分弦
④平分弦所对优弧
⑤平分弦所对劣弧
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所
对的两条弧。
①
⑤
③④②
①
④
③②⑤
①③
②④⑤
①
④
⑤
②
③
(3)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分
弦所对的另一条弧。
①②
③④⑤
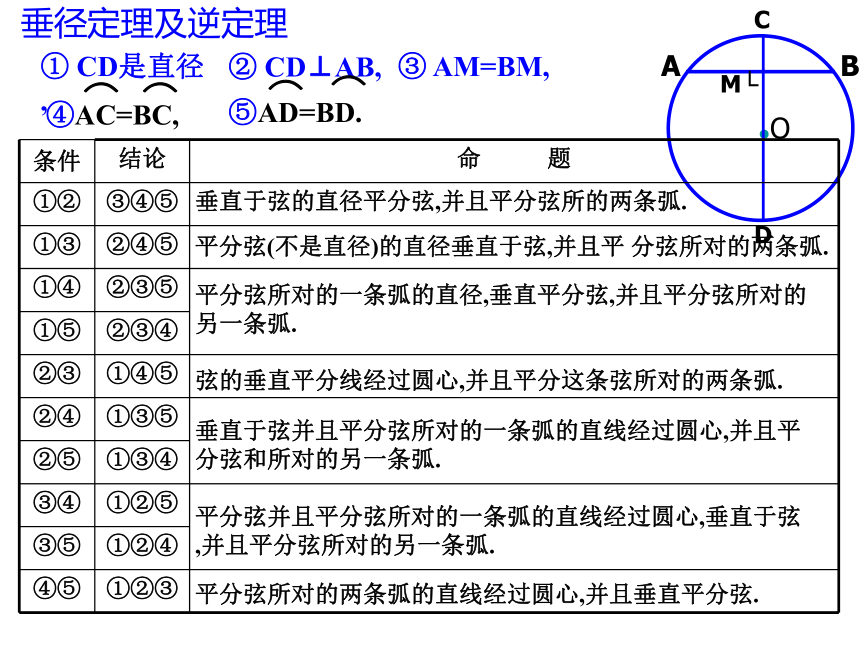
垂径定理及逆定理
●O
A
B
C
D
M└
条件 结论 命 题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④
②③ ①④⑤
②④ ①③⑤
②⑤ ①③④
③④ ①②⑤
③⑤ ①②④
④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
根据垂径定理与推论可知:对于一个圆和一条直线来说,如果具备:
那么,由五个条件中的任何两个条件都可以推出其他三个结论。
注意要点
① 经过圆心
② 垂直于弦
③ 平分弦
④ 平分弦所对的优弧
⑤ 平分弦所对的劣弧
(注意特殊例外)
1.判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
圆内两条非直径的弦不能互相平分
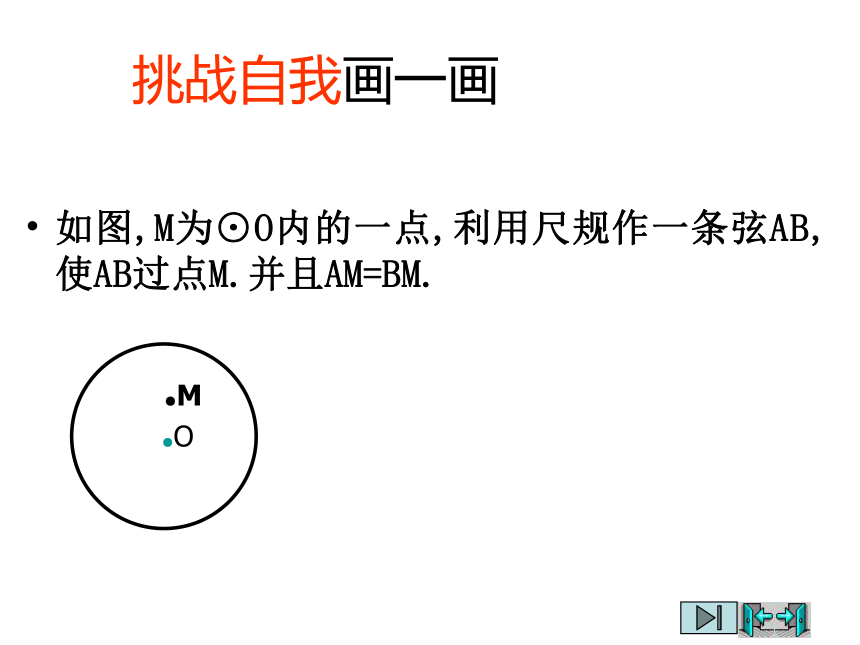
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
练习1.如图,⊙O的直径是10,弦 AB的长为8,P是AB上的一个动点,
①则OP的求值范围是 。
②使线段OP的长度为整数值的P点
位置有 个。
p1
p2
P
C
注意圆的轴对称性
3≤OP≤5
5
练习2.如上图,⊙O的直径是10,
线段OP的长为3,则过点P的所有弦中,①最大弦长为 ,
②最短弦长为 ,③弦长为整数
的有 条?
A
B
C
D
连半径,构造
直角三角形
平分已知弧 AB .
你会四等分弧AB吗
A
B
已知:⊙O中弦AB∥CD.
求证:AC=BD
⌒
⌒
证明:作直径MN⊥AB。∵AB∥CD,∴MN⊥CD。则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弦)
AM-CM = BM -DM
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
C
D
A
B
O
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?
圆的两条平行弦所夹的弧相等
⌒
M
N
如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD
求证:△OCD为等腰三角形。
E
如图,两个圆都以点O为圆心,小圆 的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系?为什么?
E
. 如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.
求证四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
(1).在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度.
E
D
┌
600
C
D
(2).在直径为650mm的圆柱形油槽内装入一些油后,截面的油面宽AB = 600mm,求油的最大深度.
B
A
O
600
650
D
C
E
D
┌
600
C
D
E
小结:
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8㎝,那么⊙o的半径是
2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD,那么C到AB的距离等于
3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1㎝,那么⊙O的半径为
4.如图,在⊙O中弦AB⊥AC,
OM⊥AB,ON⊥AC,垂足分别为M,
N,且OM=2,0N=3,则AB= ,
AC= ,OA=
B
A
M
C
O
N
5㎝
1㎝或9㎝
6
4
Cm
练习
1.已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF
.
A
O
B
E
C
D
F
3.如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝.
求AE-BF的长.
2. 如图,CD为圆O的直径,弦AB
交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长.
思考题:船能过拱桥吗
如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
在Rt△OAD中,由勾股定理,得
解得 R≈3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
11.2三角形全等的判定 (ASA)(AAS)
24.2.2垂径定理
垂径定理
定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所
对的两条弧。
课堂讨论
根据已知条件进行推导:
①过圆心
②垂直于弦
③平分弦
④平分弦所对优弧
⑤平分弦所对劣弧
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所
对的两条弧。
①
⑤
③④②
①
④
③②⑤
①③
②④⑤
①
④
⑤
②
③
(3)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分
弦所对的另一条弧。
①②
③④⑤
垂径定理及逆定理
●O
A
B
C
D
M└
条件 结论 命 题
①② ③④⑤
①③ ②④⑤
①④ ②③⑤
①⑤ ②③④
②③ ①④⑤
②④ ①③⑤
②⑤ ①③④
③④ ①②⑤
③⑤ ①②④
④⑤ ①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
根据垂径定理与推论可知:对于一个圆和一条直线来说,如果具备:
那么,由五个条件中的任何两个条件都可以推出其他三个结论。
注意要点
① 经过圆心
② 垂直于弦
③ 平分弦
④ 平分弦所对的优弧
⑤ 平分弦所对的劣弧
(注意特殊例外)
1.判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
圆内两条非直径的弦不能互相平分
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
练习1.如图,⊙O的直径是10,弦 AB的长为8,P是AB上的一个动点,
①则OP的求值范围是 。
②使线段OP的长度为整数值的P点
位置有 个。
p1
p2
P
C
注意圆的轴对称性
3≤OP≤5
5
练习2.如上图,⊙O的直径是10,
线段OP的长为3,则过点P的所有弦中,①最大弦长为 ,
②最短弦长为 ,③弦长为整数
的有 条?
A
B
C
D
连半径,构造
直角三角形
平分已知弧 AB .
你会四等分弧AB吗
A
B
已知:⊙O中弦AB∥CD.
求证:AC=BD
⌒
⌒
证明:作直径MN⊥AB。∵AB∥CD,∴MN⊥CD。则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弦)
AM-CM = BM -DM
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
C
D
A
B
O
如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?
圆的两条平行弦所夹的弧相等
⌒
M
N
如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD
求证:△OCD为等腰三角形。
E
如图,两个圆都以点O为圆心,小圆 的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系?为什么?
E
. 如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.
求证四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
(1).在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,求油的最大深度.
E
D
┌
600
C
D
(2).在直径为650mm的圆柱形油槽内装入一些油后,截面的油面宽AB = 600mm,求油的最大深度.
B
A
O
600
650
D
C
E
D
┌
600
C
D
E
小结:
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8㎝,那么⊙o的半径是
2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD,那么C到AB的距离等于
3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1㎝,那么⊙O的半径为
4.如图,在⊙O中弦AB⊥AC,
OM⊥AB,ON⊥AC,垂足分别为M,
N,且OM=2,0N=3,则AB= ,
AC= ,OA=
B
A
M
C
O
N
5㎝
1㎝或9㎝
6
4
Cm
练习
1.已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF
.
A
O
B
E
C
D
F
3.如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝.
求AE-BF的长.
2. 如图,CD为圆O的直径,弦AB
交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长.
思考题:船能过拱桥吗
如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
在Rt△OAD中,由勾股定理,得
解得 R≈3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
