图形的旋转
图片预览



文档简介
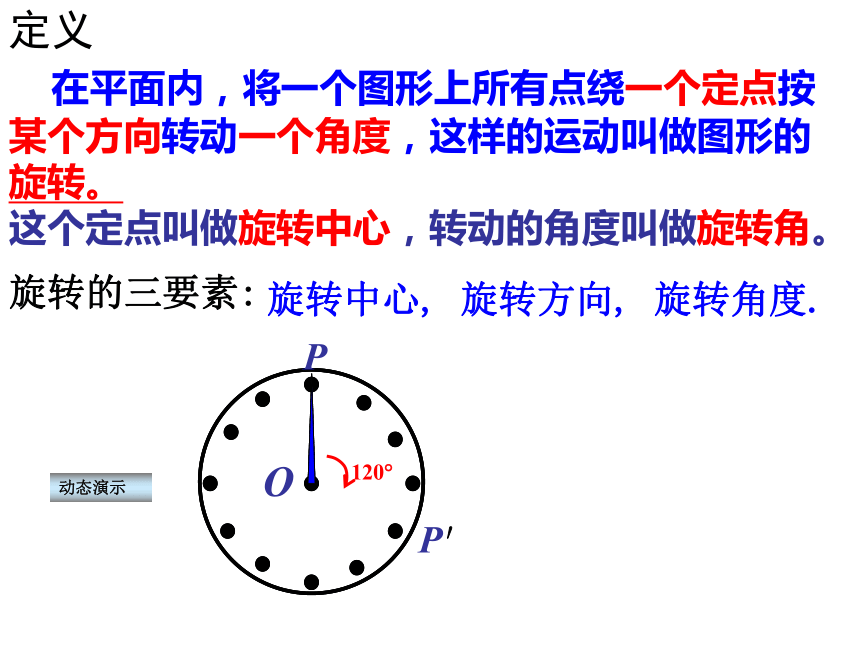
课件15张PPT。图形的图形的旋转定义动态演示OP′P 在平面内,将一个图形上所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转。
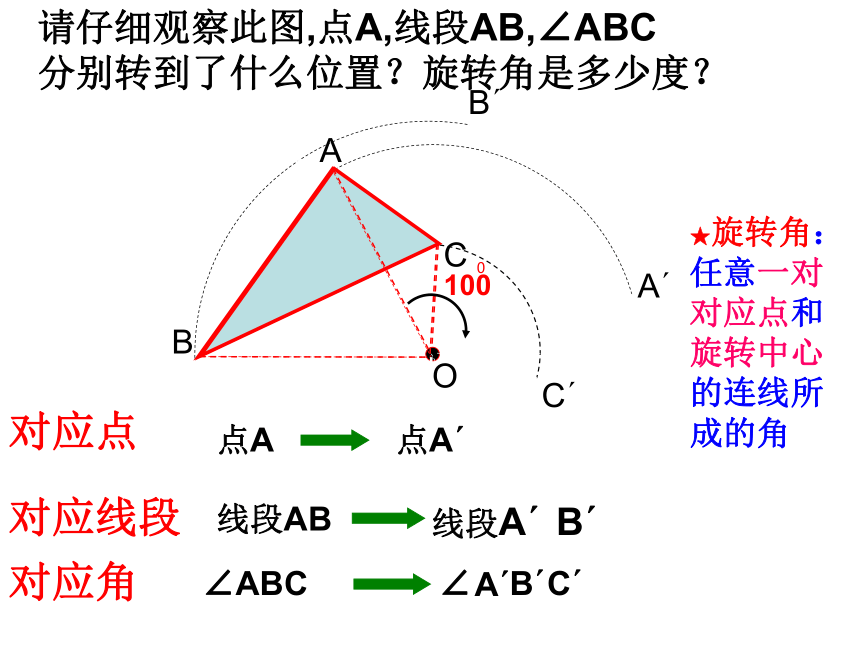
这个定点叫做旋转中心,转动的角度叫做旋转角。旋转的三要素:旋转中心,旋转方向,旋转角度.BAB′A′CC′O请仔细观察此图,点A,线段AB,∠ABC
分别转到了什么位置?旋转角是多少度?点A′点A对应点对应线段对应角★旋转角:
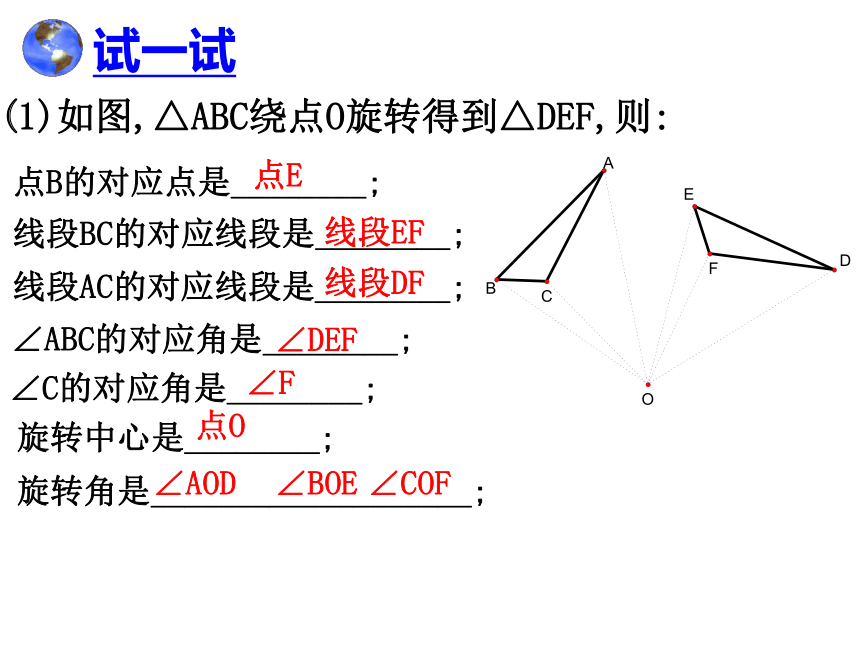
任意一对对应点和旋转中心的连线所成的角 试一试 (1)如图,△ABC绕点O旋转得到△DEF,则:点E线段EF线段DF∠DEF∠F点O∠AOD∠BOE∠COF1.线段AO与线段DO, 它们的长度相等吗?
2.线段AC与线段DF,∠A与∠D它们也相等吗?
3.你还能发现其它相等的线段或相等的角吗?量一量想一想(4)旋转不改变图形的大小和形状.旋转的基本性质
(2)对应点到旋转中心的距离相等.(3)对应线段的长度、对应角的大小相等(1)图形上的每一点都绕旋转中心 沿相同方向转动了相同的角度思考:如何作出点A绕点O顺时针旋转90°后的对应点A’呢?O⑴.连接OA⑵.作∠AOB=90°,
在OB上截取OA’=OAB(3) 点A’就是点A绕
点O旋转90°后的对应点90°做一做:1.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。BAO⑴.连接OA⑵.作∠AOC=100°,在OC上截取OA’=OA⑷.作∠BOD=100°,在OD上截取OB’=OB⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。CD⑶.连接OB注:作旋转后的图形可以转化为作旋转后的对应点O2.如图:画出△ABC绕点O按顺时针方向旋转60°后的对应的三角形。1.联结AO,BO,CO2.以OA为始边顺时针方向作∠AOM=60°,在OM截取线段OD,使OD=OA. 3.同样的方法分别可得B,C的对应点E,F。4.联结DE,EF,FD.
△DEF就是△ABC绕点O按顺时针方向旋转60°后的对应的三角形。做一做:课堂回顾:这节课,主要学习了什么?在平面内,将一个图形上所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转。旋转的概念:旋转的性质:(4)旋转不改变图形的大小和形状.(2)对应点到旋转中心的距离相等.(3)对应线段的长度、对应角的大小相等(1)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度旋转的三要素:旋转中心 旋转方向 旋转角度1.画出下图以O为旋转中心按逆时针方向旋转90°后的图形。画一画:2.请同桌设计一个图形旋转的题目,交换画出旋转后的图形。如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,动手试一下,你能写出几种方案?ABCDEF·O探究1.解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°. 本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 18002次 1200 , 2400 5次 600, 1200, 1800, 2400, 3000
3个 1次 600探究2.1.书 P100 1,2 (画在学案的反面)
2. 作图:
(1)以点B为旋转中心,顺时针旋转180°
(2)以线段AC中点为旋转中心,逆时针旋转240°
课后作业
这个定点叫做旋转中心,转动的角度叫做旋转角。旋转的三要素:旋转中心,旋转方向,旋转角度.BAB′A′CC′O请仔细观察此图,点A,线段AB,∠ABC
分别转到了什么位置?旋转角是多少度?点A′点A对应点对应线段对应角★旋转角:
任意一对对应点和旋转中心的连线所成的角 试一试 (1)如图,△ABC绕点O旋转得到△DEF,则:点E线段EF线段DF∠DEF∠F点O∠AOD∠BOE∠COF1.线段AO与线段DO, 它们的长度相等吗?
2.线段AC与线段DF,∠A与∠D它们也相等吗?
3.你还能发现其它相等的线段或相等的角吗?量一量想一想(4)旋转不改变图形的大小和形状.旋转的基本性质
(2)对应点到旋转中心的距离相等.(3)对应线段的长度、对应角的大小相等(1)图形上的每一点都绕旋转中心 沿相同方向转动了相同的角度思考:如何作出点A绕点O顺时针旋转90°后的对应点A’呢?O⑴.连接OA⑵.作∠AOB=90°,
在OB上截取OA’=OAB(3) 点A’就是点A绕
点O旋转90°后的对应点90°做一做:1.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。BAO⑴.连接OA⑵.作∠AOC=100°,在OC上截取OA’=OA⑷.作∠BOD=100°,在OD上截取OB’=OB⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。CD⑶.连接OB注:作旋转后的图形可以转化为作旋转后的对应点O2.如图:画出△ABC绕点O按顺时针方向旋转60°后的对应的三角形。1.联结AO,BO,CO2.以OA为始边顺时针方向作∠AOM=60°,在OM截取线段OD,使OD=OA. 3.同样的方法分别可得B,C的对应点E,F。4.联结DE,EF,FD.
△DEF就是△ABC绕点O按顺时针方向旋转60°后的对应的三角形。做一做:课堂回顾:这节课,主要学习了什么?在平面内,将一个图形上所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转。旋转的概念:旋转的性质:(4)旋转不改变图形的大小和形状.(2)对应点到旋转中心的距离相等.(3)对应线段的长度、对应角的大小相等(1)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度旋转的三要素:旋转中心 旋转方向 旋转角度1.画出下图以O为旋转中心按逆时针方向旋转90°后的图形。画一画:2.请同桌设计一个图形旋转的题目,交换画出旋转后的图形。如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,动手试一下,你能写出几种方案?ABCDEF·O探究1.解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°. 本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?
还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?
3个 1次 18002次 1200 , 2400 5次 600, 1200, 1800, 2400, 3000
3个 1次 600探究2.1.书 P100 1,2 (画在学案的反面)
2. 作图:
(1)以点B为旋转中心,顺时针旋转180°
(2)以线段AC中点为旋转中心,逆时针旋转240°
课后作业
