23.1 图形的旋转 第2课时 旋转性质的应用 同步练习(含答案)
文档属性
| 名称 | 23.1 图形的旋转 第2课时 旋转性质的应用 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 393.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 14:55:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
23.1 图形的旋转
第2课时 旋转性质的应用
基础提优题
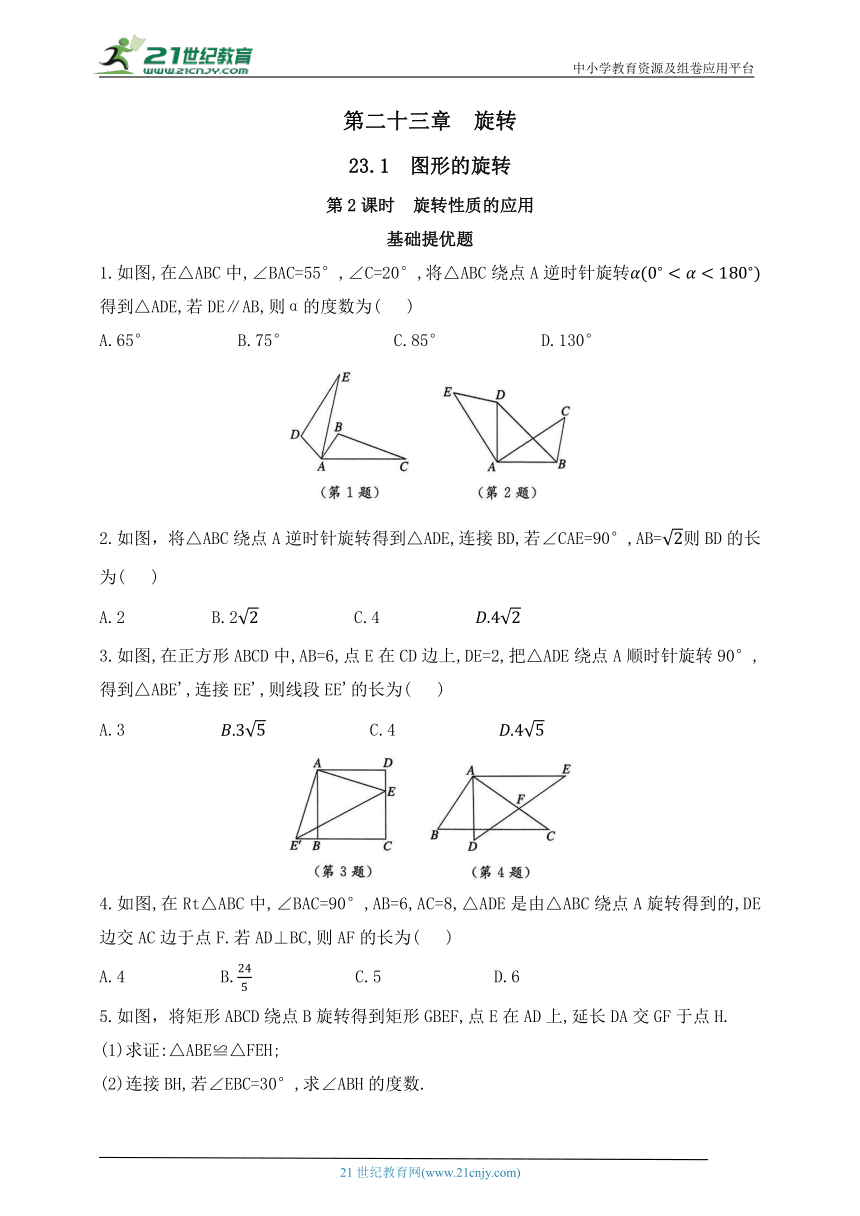
1.如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转得到△ADE,若DE∥AB,则α的度数为( )
A.65° B.75° C.85° D.130°
2.如图,将△ABC绕点A逆时针旋转得到△ADE,连接BD,若∠CAE=90°,AB=则BD的长为( )
A.2 B.2 C.4
3.如图,在正方形ABCD中,AB=6,点E在CD边上,DE=2,把△ADE绕点A顺时针旋转90°,得到△ABE',连接EE',则线段EE'的长为( )
A.3 C.4
4.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,△ADE是由△ABC绕点A旋转得到的,DE边交AC边于点F.若AD⊥BC,则AF的长为( )
A.4 B. C.5 D.6
5.如图,将矩形ABCD绕点B旋转得到矩形GBEF,点E在AD上,延长DA交GF于点H.
(1)求证:△ABE≌△FEH;
(2)连接BH,若∠EBC=30°,求∠ABH的度数.
综合应用题
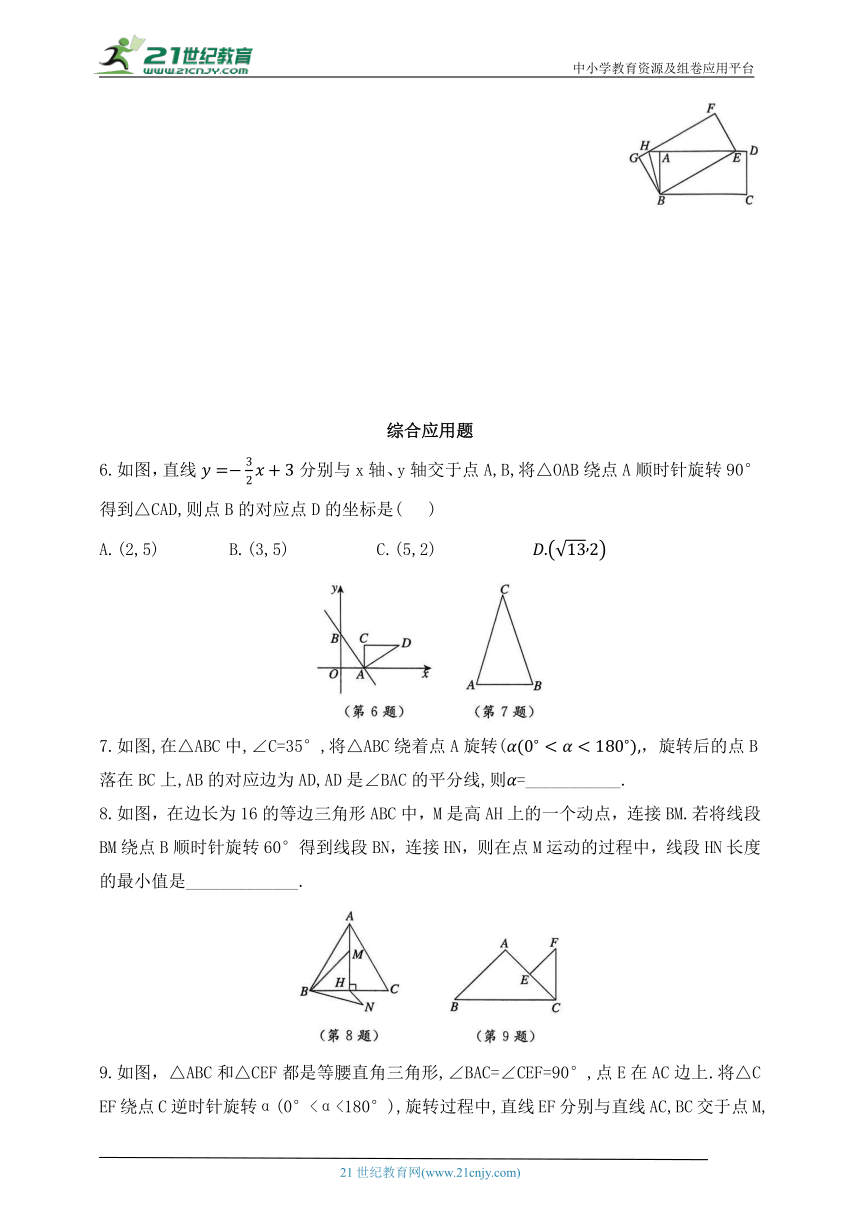
6.如图,直线分别与x轴、y轴交于点A,B,将△OAB绕点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是( )
A.(2,5) B.(3,5) C.(5,2)
7.如图,在△ABC中,∠C=35°,将△ABC绕着点A旋转(,旋转后的点B落在BC上,AB的对应边为AD,AD是∠BAC的平分线,则=___________.
8.如图,在边长为16的等边三角形ABC中,M是高AH上的一个动点,连接BM.若将线段BM绕点B顺时针旋转60°得到线段BN,连接HN,则在点M运动的过程中,线段HN长度的最小值是_____________.
9.如图,△ABC和△CEF都是等腰直角三角形,∠BAC=∠CEF=90°,点E在AC边上.将△CEF绕点C逆时针旋转α(0°<α<180°),旋转过程中,直线EF分别与直线AC,BC交于点M,N,若△CMN是等腰三角形,则的度数为____________.
10.如图,点E是矩形ABCD的边BC上一点,将△ABE绕点A逆时针旋转至△AB E 的位置,此时E,B ,E 三点恰好共线.点M,N分别是AE和AE 的中点,连接MN,NB .
(1)求证:四边形MEB N是平行四边形;
(2)延长EE 交AD于点F,若.S△AE F=S△CB E,判断△AE F与△CB E是否全等,并说明理由.
创新拓展题
11.(1)【问题发现】如图①,△ABC和△ECD都是等边三角形,点B,C,D在同一直线上,连接BE,AD相交于点F.
填空:
①线段BE与AD之间的数量关系为_____________;
②∠AFB的度数为_____________.
(2)【拓展探究】
当△ECD绕点C逆时针旋转到图②的位置时,(1)中的两个结论是否还成立 请根据图②的情形给出证明.
(3)【问题解决】
已知若△ECD绕点C逆时针旋转一周,当点E位于线段AC的垂直平分线上时,请直接写出△ACD的面积.
参考答案
1.B 2.A 3.D
4.C 【点拨】在△ABC中,∠BAC=90°,AB=6,AC=8,
由旋转的性质得∠E=∠C,∠DAE=∠BAC=90°,DE=BC=10,
∵AD⊥BC,∴易得AE∥BC.∴∠EAC=∠C.∴∠E=∠EAC.∴AF=EF.
∵∠E+∠D=∠DAF+∠EAF=90°,∴∠D=∠DAF.∴AF=DF.
∴易得AF为Rt△ADE的中线.
5.(1)【证明】∵四边形ABCD是矩形,∴AB=DC,∠BAE=∠D=90°.
由旋转得FE=DC,∠F=∠D=90°.∴AB=FE,∠BAE=∠F.
在矩形BEFG中,GF∥BE,∴∠AEB=∠FHE.∴△ABE≌△FEH(AAS).
(2)【解】∵四边形ABCD是矩形,∴AD∥BC,∠DAB=∠HAB=90°.
∴∠HEB=∠EBC=30°.
∵△ABE≌△FEH,∴BE=EH.
6.C
【点拨】如图,△ABC绕着点A旋转α后得到△ADE.
由旋转得∠BAD=α,AB=AD.
∵AD是∠BAC的平分线,∴∠CAD=∠BAD=α.∴∠ADB=∠C+∠CAD=35°+α.
∵AB=AD,∴∠B=∠ADB=35°+α.
在△ABC中,∠C+∠CAB+解得
8.4【点拨】如图,取AB的中点G,连接MG,则
∵线段BM绕点B顺时针旋转60°得到线段BN,∴∠MBH+∠HBN=60°,BM=BN.∵△ABC是等边三角形,∴∠ABC=∠BAC=60°,AB=BC.
∴∠MBH+∠MBG=60°.∴∠HBN=∠GBM.
∵AH是等边三角形ABC的高,∴BH=
△NBH.∴MG=NH.
根据垂线段最短可知,当GM⊥AH时,MG最短,即HN最短.
30°,∴当GM⊥AH时,
即线段HN长度的最小值是4.
9.22.5°或45°或112.5°【点拨】依题意可知∠ACB=45°.
如图①,当CM=CN且点E在∠ACB内部时,
∵CM=CN,
如图②,当NM=NC时,点N与点E重合,点M与点F重合,α=∠MCN=∠ACB=45°;如图③,当CN=CM且点E在∠ACB外部时,
∵CM=CN,EF⊥CE,∴∠NCE=
.
综上所述,满足条件的α的度数为22.5°或45°或112.5°.
10.(1)【证明】∵四边形ABCD是矩形,∴∠B=90°.
∵△AB E 是△ABE旋转所得的,∴AE=AE ,∠AB E =
∴B是EE 的中点,
∵M,N分别是AE和AE 的中点,∴MN∥EB ,MN=
∴四边形MEB N为平行四边形.
(2)【解】△AE F≌△CB E,理由:连接FC.
同理
∥∠FEC,△AEF底边AF上的高和△FEC底边EC上的高相等,∴AF=EC.
在△AE F和△CB E中,
11.【解】(1)①AD=BE②60°
(2)(1)中的两个结论仍成立.
证明:∵△ABC是等边三角形,∴AC=BC,∠ACB=60°.
∵△ECD是等边三角形,∴CE=CD,∠DCE=60°.∴∠ACB=∠DCE.
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD.∴BE=AD,∠CBE=∠CAD.
设BE交AC于点O,
∵180°-∠BOC=∠ACB+∠CBE,且∠ACB=60°,∴∠AFB=∠ACB=60°.
(3)△ACD的面积为2或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十三章 旋转
23.1 图形的旋转
第2课时 旋转性质的应用
基础提优题
1.如图,在△ABC中,∠BAC=55°,∠C=20°,将△ABC绕点A逆时针旋转得到△ADE,若DE∥AB,则α的度数为( )
A.65° B.75° C.85° D.130°
2.如图,将△ABC绕点A逆时针旋转得到△ADE,连接BD,若∠CAE=90°,AB=则BD的长为( )
A.2 B.2 C.4
3.如图,在正方形ABCD中,AB=6,点E在CD边上,DE=2,把△ADE绕点A顺时针旋转90°,得到△ABE',连接EE',则线段EE'的长为( )
A.3 C.4
4.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,△ADE是由△ABC绕点A旋转得到的,DE边交AC边于点F.若AD⊥BC,则AF的长为( )
A.4 B. C.5 D.6
5.如图,将矩形ABCD绕点B旋转得到矩形GBEF,点E在AD上,延长DA交GF于点H.
(1)求证:△ABE≌△FEH;
(2)连接BH,若∠EBC=30°,求∠ABH的度数.
综合应用题
6.如图,直线分别与x轴、y轴交于点A,B,将△OAB绕点A顺时针旋转90°得到△CAD,则点B的对应点D的坐标是( )
A.(2,5) B.(3,5) C.(5,2)
7.如图,在△ABC中,∠C=35°,将△ABC绕着点A旋转(,旋转后的点B落在BC上,AB的对应边为AD,AD是∠BAC的平分线,则=___________.
8.如图,在边长为16的等边三角形ABC中,M是高AH上的一个动点,连接BM.若将线段BM绕点B顺时针旋转60°得到线段BN,连接HN,则在点M运动的过程中,线段HN长度的最小值是_____________.
9.如图,△ABC和△CEF都是等腰直角三角形,∠BAC=∠CEF=90°,点E在AC边上.将△CEF绕点C逆时针旋转α(0°<α<180°),旋转过程中,直线EF分别与直线AC,BC交于点M,N,若△CMN是等腰三角形,则的度数为____________.
10.如图,点E是矩形ABCD的边BC上一点,将△ABE绕点A逆时针旋转至△AB E 的位置,此时E,B ,E 三点恰好共线.点M,N分别是AE和AE 的中点,连接MN,NB .
(1)求证:四边形MEB N是平行四边形;
(2)延长EE 交AD于点F,若.S△AE F=S△CB E,判断△AE F与△CB E是否全等,并说明理由.
创新拓展题
11.(1)【问题发现】如图①,△ABC和△ECD都是等边三角形,点B,C,D在同一直线上,连接BE,AD相交于点F.
填空:
①线段BE与AD之间的数量关系为_____________;
②∠AFB的度数为_____________.
(2)【拓展探究】
当△ECD绕点C逆时针旋转到图②的位置时,(1)中的两个结论是否还成立 请根据图②的情形给出证明.
(3)【问题解决】
已知若△ECD绕点C逆时针旋转一周,当点E位于线段AC的垂直平分线上时,请直接写出△ACD的面积.
参考答案
1.B 2.A 3.D
4.C 【点拨】在△ABC中,∠BAC=90°,AB=6,AC=8,
由旋转的性质得∠E=∠C,∠DAE=∠BAC=90°,DE=BC=10,
∵AD⊥BC,∴易得AE∥BC.∴∠EAC=∠C.∴∠E=∠EAC.∴AF=EF.
∵∠E+∠D=∠DAF+∠EAF=90°,∴∠D=∠DAF.∴AF=DF.
∴易得AF为Rt△ADE的中线.
5.(1)【证明】∵四边形ABCD是矩形,∴AB=DC,∠BAE=∠D=90°.
由旋转得FE=DC,∠F=∠D=90°.∴AB=FE,∠BAE=∠F.
在矩形BEFG中,GF∥BE,∴∠AEB=∠FHE.∴△ABE≌△FEH(AAS).
(2)【解】∵四边形ABCD是矩形,∴AD∥BC,∠DAB=∠HAB=90°.
∴∠HEB=∠EBC=30°.
∵△ABE≌△FEH,∴BE=EH.
6.C
【点拨】如图,△ABC绕着点A旋转α后得到△ADE.
由旋转得∠BAD=α,AB=AD.
∵AD是∠BAC的平分线,∴∠CAD=∠BAD=α.∴∠ADB=∠C+∠CAD=35°+α.
∵AB=AD,∴∠B=∠ADB=35°+α.
在△ABC中,∠C+∠CAB+解得
8.4【点拨】如图,取AB的中点G,连接MG,则
∵线段BM绕点B顺时针旋转60°得到线段BN,∴∠MBH+∠HBN=60°,BM=BN.∵△ABC是等边三角形,∴∠ABC=∠BAC=60°,AB=BC.
∴∠MBH+∠MBG=60°.∴∠HBN=∠GBM.
∵AH是等边三角形ABC的高,∴BH=
△NBH.∴MG=NH.
根据垂线段最短可知,当GM⊥AH时,MG最短,即HN最短.
30°,∴当GM⊥AH时,
即线段HN长度的最小值是4.
9.22.5°或45°或112.5°【点拨】依题意可知∠ACB=45°.
如图①,当CM=CN且点E在∠ACB内部时,
∵CM=CN,
如图②,当NM=NC时,点N与点E重合,点M与点F重合,α=∠MCN=∠ACB=45°;如图③,当CN=CM且点E在∠ACB外部时,
∵CM=CN,EF⊥CE,∴∠NCE=
.
综上所述,满足条件的α的度数为22.5°或45°或112.5°.
10.(1)【证明】∵四边形ABCD是矩形,∴∠B=90°.
∵△AB E 是△ABE旋转所得的,∴AE=AE ,∠AB E =
∴B是EE 的中点,
∵M,N分别是AE和AE 的中点,∴MN∥EB ,MN=
∴四边形MEB N为平行四边形.
(2)【解】△AE F≌△CB E,理由:连接FC.
同理
∥∠FEC,△AEF底边AF上的高和△FEC底边EC上的高相等,∴AF=EC.
在△AE F和△CB E中,
11.【解】(1)①AD=BE②60°
(2)(1)中的两个结论仍成立.
证明:∵△ABC是等边三角形,∴AC=BC,∠ACB=60°.
∵△ECD是等边三角形,∴CE=CD,∠DCE=60°.∴∠ACB=∠DCE.
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD.∴BE=AD,∠CBE=∠CAD.
设BE交AC于点O,
∵180°-∠BOC=∠ACB+∠CBE,且∠ACB=60°,∴∠AFB=∠ACB=60°.
(3)△ACD的面积为2或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
