23.2 中心对称 第1课时 中心对称 同步练习(含答案)
文档属性
| 名称 | 23.2 中心对称 第1课时 中心对称 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
23.2 中心对称
第1课时 中心对称
基础提优题
1.若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;
②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;
④将一个图形绕对称中心旋转180°后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,△ABC与△A B C 关于点O成中心对称,下列说法:
①∠BAC=∠B A C ;②AC=A C ;③OA=OA ;
④△ABC与△A B C 的面积相等.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在平面直角坐标系中,若△ABC与△A B C 关于点E成中心对称,则对称中心点E的坐标是( )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
4.如图,在7×6的正方形网格中,点A,B,C,D都在格点上,请你按要求画出图形.
(1)在图①中作出△A B C ,使△A B C 和△ABC关于点D成中心对称;
(2)在图②中分别找两个格点C ,D ,使得以A,B,C ,D 为顶点的四边形为平行四边形,并且平行四边形的面积为△ABC面积的4倍.
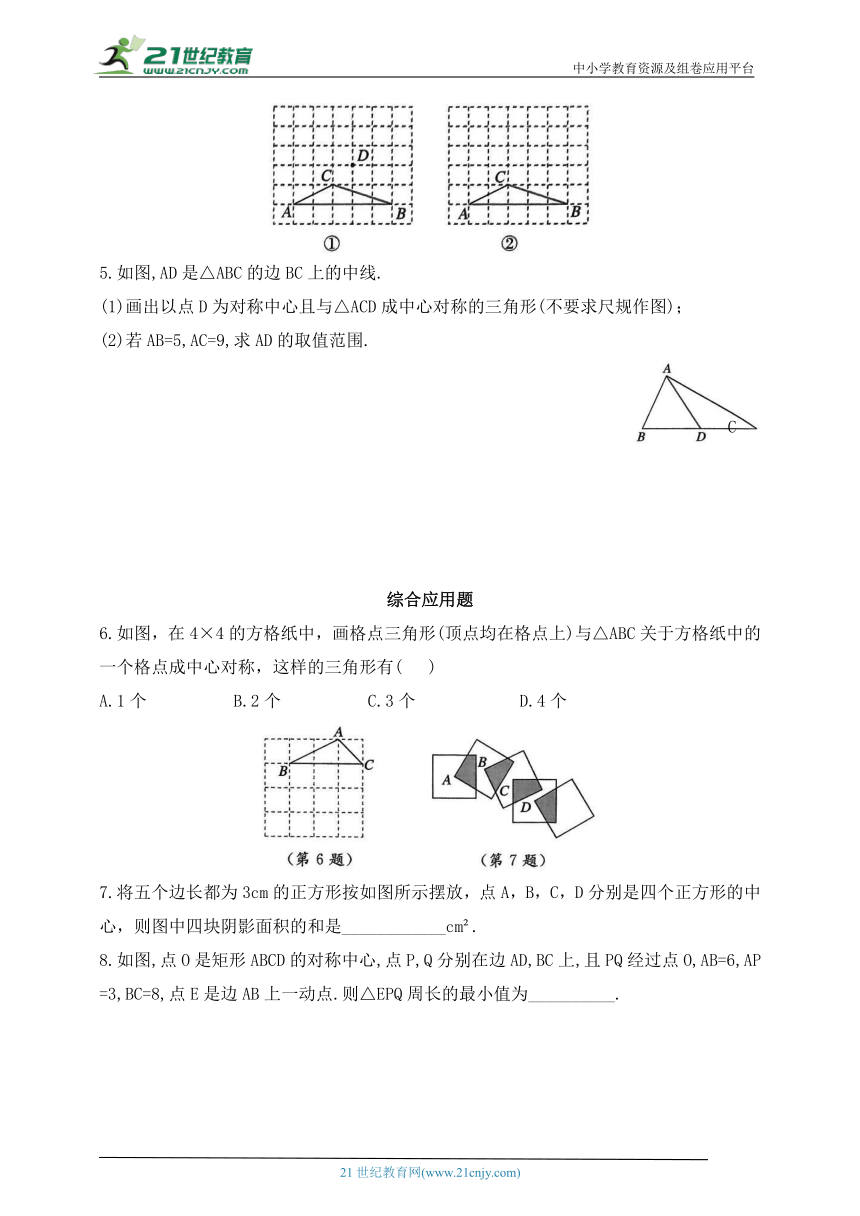
5.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心且与△ACD成中心对称的三角形(不要求尺规作图);
(2)若AB=5,AC=9,求AD的取值范围.
综合应用题
6.如图,在4×4的方格纸中,画格点三角形(顶点均在格点上)与△ABC关于方格纸中的一个格点成中心对称,这样的三角形有( )
A.1个 B.2个 C.3个 D.4个
7.将五个边长都为3cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影面积的和是____________cm .
8.如图,点O是矩形ABCD的对称中心,点P,Q分别在边AD,BC上,且PQ经过点O,AB=6,AP=3,BC=8,点E是边AB上一动点.则△EPQ周长的最小值为__________.
9.将边长为6的正方形的右上角剪去一个边长为2的小正方形,把它放在如图所示的平面直角坐标系xOy中.若直线经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线的函数解析式为____________________.
10.如图,△ABC和△DEF关于点O成中心对称.
(1)找出它们的对称中心;
(2)若AC=6,AB=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
创新拓展题
11.如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A,C的坐标分别为 ,现将矩形ABCD向右平移4个单位长度,再向上平移个单位长度得到矩形EFGH.
(1)若a=4,请求出点H的坐标;
(2)若矩形ABCD与矩形EFGH关于点P中心对称,且点P的坐标为(-3,m),求m的值(用含a的代数式表示).
参考答案
1.D 2.D 3.A
4.【解】(1)如图①,△A B C 即为所求.
(2)如图②,C ,D 为满足条件的格点.(答案不唯一)
5.【解】(1)如图所示的△A'BD即是符合条件的三角形.
(2)由(1)知,△ACD和△A'BD关于点D成中心对称,
∴由中心对称的性质可知△ACD≌△A'BD.
∴A'B=AC=9,A'D=AD.
在△ABA'中,
即
∴,即.
6.B【点拨】如图所示,△A B C 即为所求.
则这样的△A B C 有2个.
7.9
【点拨】如图,作点P关于AB的对称点P',连接P'Q,交AB于点E,
此时△EPQ的周长最小,∴P'E=PE.∴PE+QE的最小值为P'Q.
∴△EPQ周长的最小值为P'Q+PQ,
过点P'作P'F⊥CB交CB的延长线于点F,过点P作PH⊥BC于点H,
∵AP=3,∴P'A=3.∴易得FB=3.
∵点O是矩形ABCD的对称中心,PQ经过点O,∴AP=CQ=3.
又∵BC=8,∴BQ=5.∴FQ=8,HQ=2.
∵P'F=AB=6,∴P'Q=10.
∵PH=AB=6,周长的最小值为
【点拨】如图,延长BC交x轴于点F,连接OB,AF,CE,DF,且CE,DF相交于点N,
易得点M(2,3)是OB,AF的交点,点N的坐标为(5,2).
∴直线把长方形OABF分割成面积相等的两部分.
∵直线将多边形OABCDE分割成面积相等的两部分,
∴直线把长方形CDEF分割成面积相等的两部分.∴直线过点N(5,2).
设直线的函数解析式为y=kx+b,则解得
∴直线的函数解析式为
10.【解】(1)如图,点O即为所求.
(2)由题意得△ABC≌△DEF,∴△DEF的周长=△ABC的周长=6+5+4=15.
(3)四边形ACDF是平行四边形.
理由:由题意得OA=OD,OC=OF,∴四边形ACDF是平行四边形.
11.【解】(1)∵四边形ABCD为矩形,且A,C的坐标分别为(-8,0),(-2,4),
∴点D的坐标为(-8,4).
∵点D(-8,4)向右平移4个单位长度,再向上平移(个)单位长度得到点H,∴点H的坐标为(-4,6).
(2)连接AG,DF,它们的交点即为点P.易知点P为AG的中点,
由题意得A(-8,0),G(2,4+a/ ),∴点P的坐标为
又∵P点的坐标为(-3,m),
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十三章 旋转
23.2 中心对称
第1课时 中心对称
基础提优题
1.若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;
②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;
④将一个图形绕对称中心旋转180°后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,△ABC与△A B C 关于点O成中心对称,下列说法:
①∠BAC=∠B A C ;②AC=A C ;③OA=OA ;
④△ABC与△A B C 的面积相等.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在平面直角坐标系中,若△ABC与△A B C 关于点E成中心对称,则对称中心点E的坐标是( )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
4.如图,在7×6的正方形网格中,点A,B,C,D都在格点上,请你按要求画出图形.
(1)在图①中作出△A B C ,使△A B C 和△ABC关于点D成中心对称;
(2)在图②中分别找两个格点C ,D ,使得以A,B,C ,D 为顶点的四边形为平行四边形,并且平行四边形的面积为△ABC面积的4倍.
5.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心且与△ACD成中心对称的三角形(不要求尺规作图);
(2)若AB=5,AC=9,求AD的取值范围.
综合应用题
6.如图,在4×4的方格纸中,画格点三角形(顶点均在格点上)与△ABC关于方格纸中的一个格点成中心对称,这样的三角形有( )
A.1个 B.2个 C.3个 D.4个
7.将五个边长都为3cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心,则图中四块阴影面积的和是____________cm .
8.如图,点O是矩形ABCD的对称中心,点P,Q分别在边AD,BC上,且PQ经过点O,AB=6,AP=3,BC=8,点E是边AB上一动点.则△EPQ周长的最小值为__________.
9.将边长为6的正方形的右上角剪去一个边长为2的小正方形,把它放在如图所示的平面直角坐标系xOy中.若直线经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线的函数解析式为____________________.
10.如图,△ABC和△DEF关于点O成中心对称.
(1)找出它们的对称中心;
(2)若AC=6,AB=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
创新拓展题
11.如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A,C的坐标分别为 ,现将矩形ABCD向右平移4个单位长度,再向上平移个单位长度得到矩形EFGH.
(1)若a=4,请求出点H的坐标;
(2)若矩形ABCD与矩形EFGH关于点P中心对称,且点P的坐标为(-3,m),求m的值(用含a的代数式表示).
参考答案
1.D 2.D 3.A
4.【解】(1)如图①,△A B C 即为所求.
(2)如图②,C ,D 为满足条件的格点.(答案不唯一)
5.【解】(1)如图所示的△A'BD即是符合条件的三角形.
(2)由(1)知,△ACD和△A'BD关于点D成中心对称,
∴由中心对称的性质可知△ACD≌△A'BD.
∴A'B=AC=9,A'D=AD.
在△ABA'中,
即
∴,即.
6.B【点拨】如图所示,△A B C 即为所求.
则这样的△A B C 有2个.
7.9
【点拨】如图,作点P关于AB的对称点P',连接P'Q,交AB于点E,
此时△EPQ的周长最小,∴P'E=PE.∴PE+QE的最小值为P'Q.
∴△EPQ周长的最小值为P'Q+PQ,
过点P'作P'F⊥CB交CB的延长线于点F,过点P作PH⊥BC于点H,
∵AP=3,∴P'A=3.∴易得FB=3.
∵点O是矩形ABCD的对称中心,PQ经过点O,∴AP=CQ=3.
又∵BC=8,∴BQ=5.∴FQ=8,HQ=2.
∵P'F=AB=6,∴P'Q=10.
∵PH=AB=6,周长的最小值为
【点拨】如图,延长BC交x轴于点F,连接OB,AF,CE,DF,且CE,DF相交于点N,
易得点M(2,3)是OB,AF的交点,点N的坐标为(5,2).
∴直线把长方形OABF分割成面积相等的两部分.
∵直线将多边形OABCDE分割成面积相等的两部分,
∴直线把长方形CDEF分割成面积相等的两部分.∴直线过点N(5,2).
设直线的函数解析式为y=kx+b,则解得
∴直线的函数解析式为
10.【解】(1)如图,点O即为所求.
(2)由题意得△ABC≌△DEF,∴△DEF的周长=△ABC的周长=6+5+4=15.
(3)四边形ACDF是平行四边形.
理由:由题意得OA=OD,OC=OF,∴四边形ACDF是平行四边形.
11.【解】(1)∵四边形ABCD为矩形,且A,C的坐标分别为(-8,0),(-2,4),
∴点D的坐标为(-8,4).
∵点D(-8,4)向右平移4个单位长度,再向上平移(个)单位长度得到点H,∴点H的坐标为(-4,6).
(2)连接AG,DF,它们的交点即为点P.易知点P为AG的中点,
由题意得A(-8,0),G(2,4+a/ ),∴点P的坐标为
又∵P点的坐标为(-3,m),
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
