23.2 中心对称 第2课时 中心对称图形 同步练习(含答案)
文档属性
| 名称 | 23.2 中心对称 第2课时 中心对称图形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 449.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 15:00:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
23.2 中心对称
第2课时 中心对称图形
基础提优题
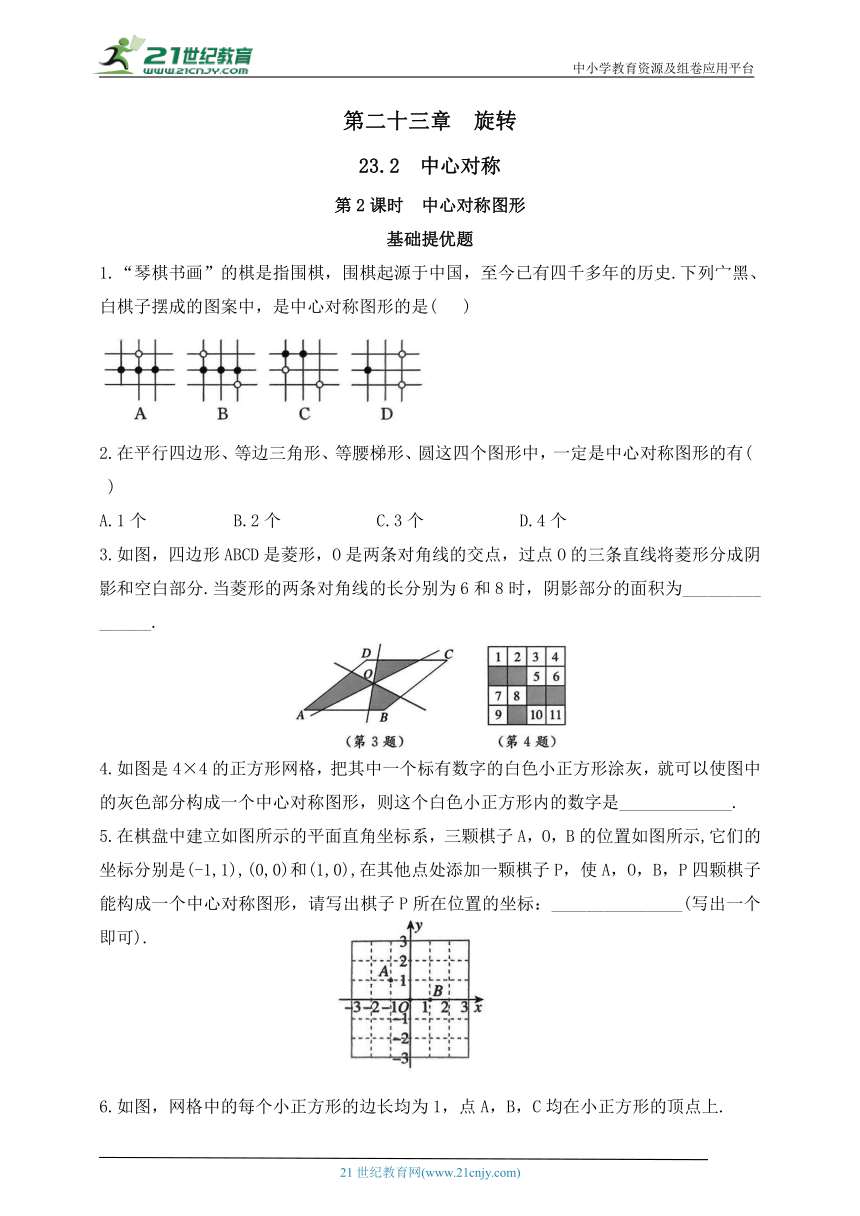
1.“琴棋书画”的棋是指围棋,围棋起源于中国,至今已有四千多年的历史.下列宀黑、白棋子摆成的图案中,是中心对称图形的是( )
2.在平行四边形、等边三角形、等腰梯形、圆这四个图形中,一定是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,阴影部分的面积为_______________.
4.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂灰,就可以使图中的灰色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____________.
5.在棋盘中建立如图所示的平面直角坐标系,三颗棋子A,O,B的位置如图所示,它们的坐标分别是(-1,1),(0,0)和(1,0),在其他点处添加一颗棋子P,使A,O,B,P四颗棋子能构成一个中心对称图形,请写出棋子P所在位置的坐标:_______________(写出一个即可).
6.如图,网格中的每个小正方形的边长均为1,点A,B,C均在小正方形的顶点上.
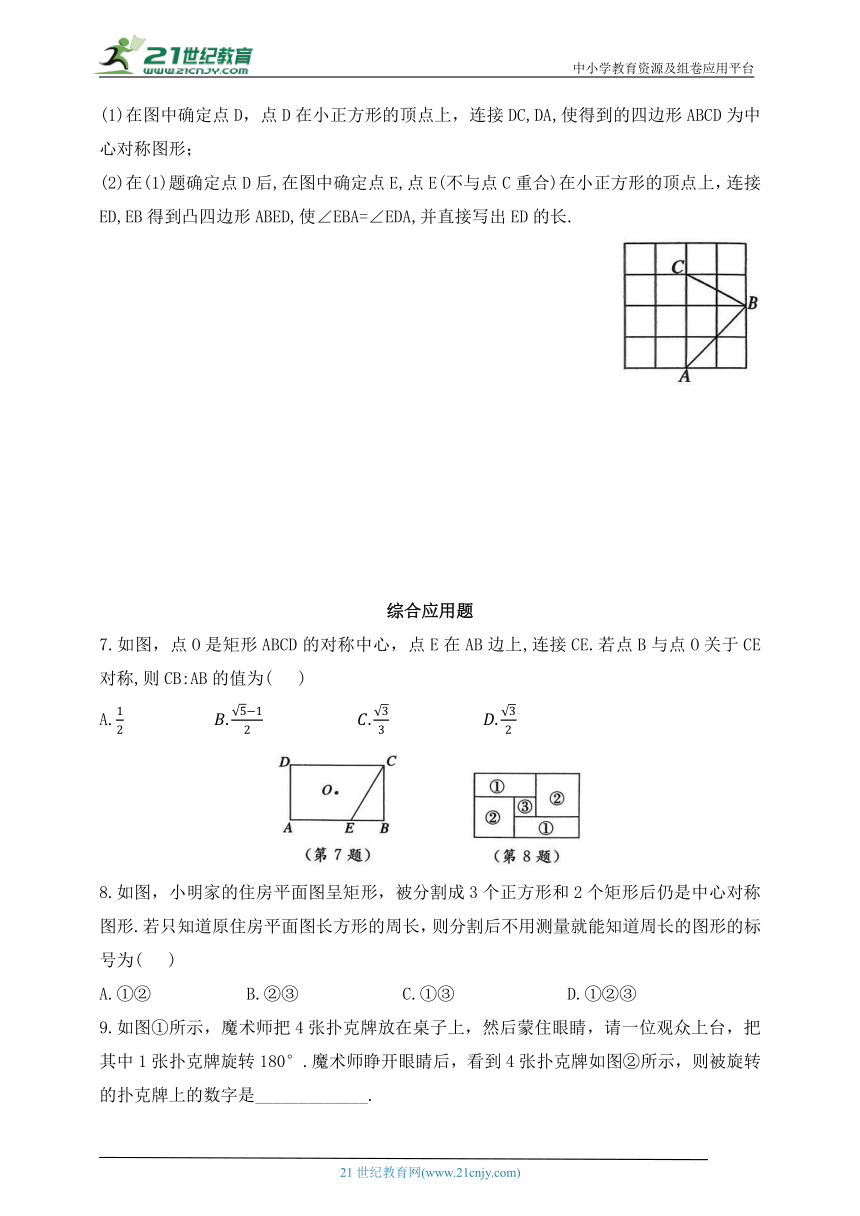
(1)在图中确定点D,点D在小正方形的顶点上,连接DC,DA,使得到的四边形ABCD为中心对称图形;
(2)在(1)题确定点D后,在图中确定点E,点E(不与点C重合)在小正方形的顶点上,连接ED,EB得到凸四边形ABED,使∠EBA=∠EDA,并直接写出ED的长.
综合应用题
7.如图,点O是矩形ABCD的对称中心,点E在AB边上,连接CE.若点B与点O关于CE对称,则CB:AB的值为( )
A.
8.如图,小明家的住房平面图呈矩形,被分割成3个正方形和2个矩形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③ C.①③ D.①②③
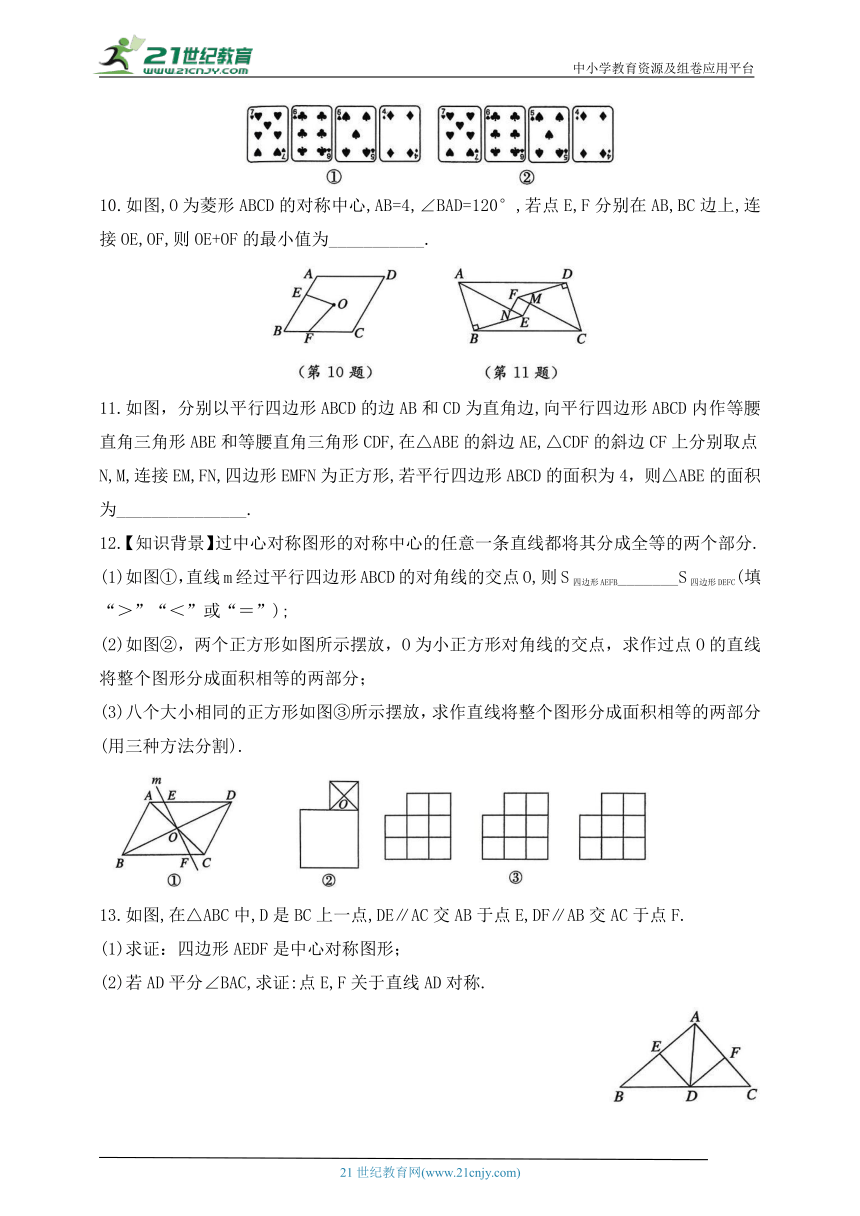
9.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把其中1张扑克牌旋转180°.魔术师睁开眼睛后,看到4张扑克牌如图②所示,则被旋转的扑克牌上的数字是_____________.
10.如图,O为菱形ABCD的对称中心,AB=4,∠BAD=120°,若点E,F分别在AB,BC边上,连接OE,OF,则OE+OF的最小值为___________.
11.如图,分别以平行四边形ABCD的边AB和CD为直角边,向平行四边形ABCD内作等腰直角三角形ABE和等腰直角三角形CDF,在△ABE的斜边AE,△CDF的斜边CF上分别取点N,M,连接EM,FN,四边形EMFN为正方形,若平行四边形ABCD的面积为4,则△ABE的面积为_______________.
12.【知识背景】过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD的对角线的交点O,则S四边形AEFB_______S四边形DEFC(填“>”“<”或“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
13.如图,在△ABC中,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E,F关于直线AD对称.
创新拓展题
14.如图,在平面直角坐标系中,□OABC的顶点A的坐标为(4,0),B的坐标为(6,2).
(1)□OABC的对称中心P的坐标为_____________;
(2)连接PA,求出直线PA的解析式;
(3)求证:不论k取何值,□OABC都被直线分成面积相等的两部分.
参考答案
1.B 2.B 3.12 4.3 5.(0,1)(答案不唯一)
6.【解】(1)如图,点D即为所求.
(2)如图,点E即为所求.
7.C【点拨】如图,连接DB,AC,OE.易知点O为AC,DB的交点.
∵四边形ABCD是矩形,∴∠ABC=90°,OC=OA=AC.
∵点B与点O关于CE对称,∴OE=EB,∠OEC=∠BEC.
在△COE和△CBE中∴△COE≌△CBE(SAS).
∴OC=CB.∴AC=2BC.
易得即
8.A【点拨】设图形①的长和宽分别是a,c,图形②的边长是b,图形③的边长是d,原矩形周长是l,则l=2(a+2b+c).
由题意可得
∴l=2(a+2b+c)=4(a+c)=8b.∴2(a+c)=,4b=
∵图形①的周长是2(a+c),图形②的周长是4b,
∴分割后不用测量就知道周长的图形的标号为①②.
9.4
10.2【点拨】连接AC.
∵四边形ABCD是菱形,∴AC过点O,BC=AB=4,∠BAD+∠B=180°.
∵∠BAD=120°,∴∠B=60°.∴△ABC是等边三角形.∴AC=4,∠BAC=∠ACB=60°.易得OA=OC=2.由垂线段最短可知,当OE⊥AB,OF⊥BC时,OE+OF的值最小,易得此时OE=的最小值为2
11.1【点拨】如图,连接EF,并延长分别交AD,BC于点G,H,连接MN与EF相交于点O.
由题意,得整个图形是以点O为对称中心的中心对称图形,
∠NEF=C∠MFE=∠BAE=∠DCF=45°,
∴,AB∥GH∥CD,
∴△ABE的面积
12.【解】(1)=(2)如图①所示.
(3)如图②所示.
13.【证明】(1)∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形.
∴四边形AEDF是中心对称图形.
(2)连接EF.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵DE∥AC,∴∠CAD=∠ADE.∴∠BAD=∠ADE.∴AE=DE.
又∵四边形AEDF是平行四边形,∴四边形AEDF是菱形.
∴AD垂直平分EF.∴点E,F关于直线AD对称.
14.(1)(3,1)
(2)【解】设直线PA的解析式为y=mx+n,
将点A(4,0),P(3,1)的坐标分别代入,得解得
∴直线PA的解析式为y=-x+4.
(3)【证明】对于直线y=kx+1-3k,
当x=3时,y=3k+1-3k=1,∴直线y=kx+1-3k过定点P(3,1).
∴不论k取何值,□OABC都被直线y=kx+1-3k分成面积相等的两部分.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十三章 旋转
23.2 中心对称
第2课时 中心对称图形
基础提优题
1.“琴棋书画”的棋是指围棋,围棋起源于中国,至今已有四千多年的历史.下列宀黑、白棋子摆成的图案中,是中心对称图形的是( )
2.在平行四边形、等边三角形、等腰梯形、圆这四个图形中,一定是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,阴影部分的面积为_______________.
4.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂灰,就可以使图中的灰色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____________.
5.在棋盘中建立如图所示的平面直角坐标系,三颗棋子A,O,B的位置如图所示,它们的坐标分别是(-1,1),(0,0)和(1,0),在其他点处添加一颗棋子P,使A,O,B,P四颗棋子能构成一个中心对称图形,请写出棋子P所在位置的坐标:_______________(写出一个即可).
6.如图,网格中的每个小正方形的边长均为1,点A,B,C均在小正方形的顶点上.
(1)在图中确定点D,点D在小正方形的顶点上,连接DC,DA,使得到的四边形ABCD为中心对称图形;
(2)在(1)题确定点D后,在图中确定点E,点E(不与点C重合)在小正方形的顶点上,连接ED,EB得到凸四边形ABED,使∠EBA=∠EDA,并直接写出ED的长.
综合应用题
7.如图,点O是矩形ABCD的对称中心,点E在AB边上,连接CE.若点B与点O关于CE对称,则CB:AB的值为( )
A.
8.如图,小明家的住房平面图呈矩形,被分割成3个正方形和2个矩形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③ C.①③ D.①②③
9.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把其中1张扑克牌旋转180°.魔术师睁开眼睛后,看到4张扑克牌如图②所示,则被旋转的扑克牌上的数字是_____________.
10.如图,O为菱形ABCD的对称中心,AB=4,∠BAD=120°,若点E,F分别在AB,BC边上,连接OE,OF,则OE+OF的最小值为___________.
11.如图,分别以平行四边形ABCD的边AB和CD为直角边,向平行四边形ABCD内作等腰直角三角形ABE和等腰直角三角形CDF,在△ABE的斜边AE,△CDF的斜边CF上分别取点N,M,连接EM,FN,四边形EMFN为正方形,若平行四边形ABCD的面积为4,则△ABE的面积为_______________.
12.【知识背景】过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD的对角线的交点O,则S四边形AEFB_______S四边形DEFC(填“>”“<”或“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
13.如图,在△ABC中,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E,F关于直线AD对称.
创新拓展题
14.如图,在平面直角坐标系中,□OABC的顶点A的坐标为(4,0),B的坐标为(6,2).
(1)□OABC的对称中心P的坐标为_____________;
(2)连接PA,求出直线PA的解析式;
(3)求证:不论k取何值,□OABC都被直线分成面积相等的两部分.
参考答案
1.B 2.B 3.12 4.3 5.(0,1)(答案不唯一)
6.【解】(1)如图,点D即为所求.
(2)如图,点E即为所求.
7.C【点拨】如图,连接DB,AC,OE.易知点O为AC,DB的交点.
∵四边形ABCD是矩形,∴∠ABC=90°,OC=OA=AC.
∵点B与点O关于CE对称,∴OE=EB,∠OEC=∠BEC.
在△COE和△CBE中∴△COE≌△CBE(SAS).
∴OC=CB.∴AC=2BC.
易得即
8.A【点拨】设图形①的长和宽分别是a,c,图形②的边长是b,图形③的边长是d,原矩形周长是l,则l=2(a+2b+c).
由题意可得
∴l=2(a+2b+c)=4(a+c)=8b.∴2(a+c)=,4b=
∵图形①的周长是2(a+c),图形②的周长是4b,
∴分割后不用测量就知道周长的图形的标号为①②.
9.4
10.2【点拨】连接AC.
∵四边形ABCD是菱形,∴AC过点O,BC=AB=4,∠BAD+∠B=180°.
∵∠BAD=120°,∴∠B=60°.∴△ABC是等边三角形.∴AC=4,∠BAC=∠ACB=60°.易得OA=OC=2.由垂线段最短可知,当OE⊥AB,OF⊥BC时,OE+OF的值最小,易得此时OE=的最小值为2
11.1【点拨】如图,连接EF,并延长分别交AD,BC于点G,H,连接MN与EF相交于点O.
由题意,得整个图形是以点O为对称中心的中心对称图形,
∠NEF=C∠MFE=∠BAE=∠DCF=45°,
∴,AB∥GH∥CD,
∴△ABE的面积
12.【解】(1)=(2)如图①所示.
(3)如图②所示.
13.【证明】(1)∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形.
∴四边形AEDF是中心对称图形.
(2)连接EF.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵DE∥AC,∴∠CAD=∠ADE.∴∠BAD=∠ADE.∴AE=DE.
又∵四边形AEDF是平行四边形,∴四边形AEDF是菱形.
∴AD垂直平分EF.∴点E,F关于直线AD对称.
14.(1)(3,1)
(2)【解】设直线PA的解析式为y=mx+n,
将点A(4,0),P(3,1)的坐标分别代入,得解得
∴直线PA的解析式为y=-x+4.
(3)【证明】对于直线y=kx+1-3k,
当x=3时,y=3k+1-3k=1,∴直线y=kx+1-3k过定点P(3,1).
∴不论k取何值,□OABC都被直线y=kx+1-3k分成面积相等的两部分.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
