第二十三章 旋转 专题 旋转中的常见几何模型(含答案)
文档属性
| 名称 | 第二十三章 旋转 专题 旋转中的常见几何模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 440.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 15:10:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十三章 旋转
专题 旋转中的常见几何模型
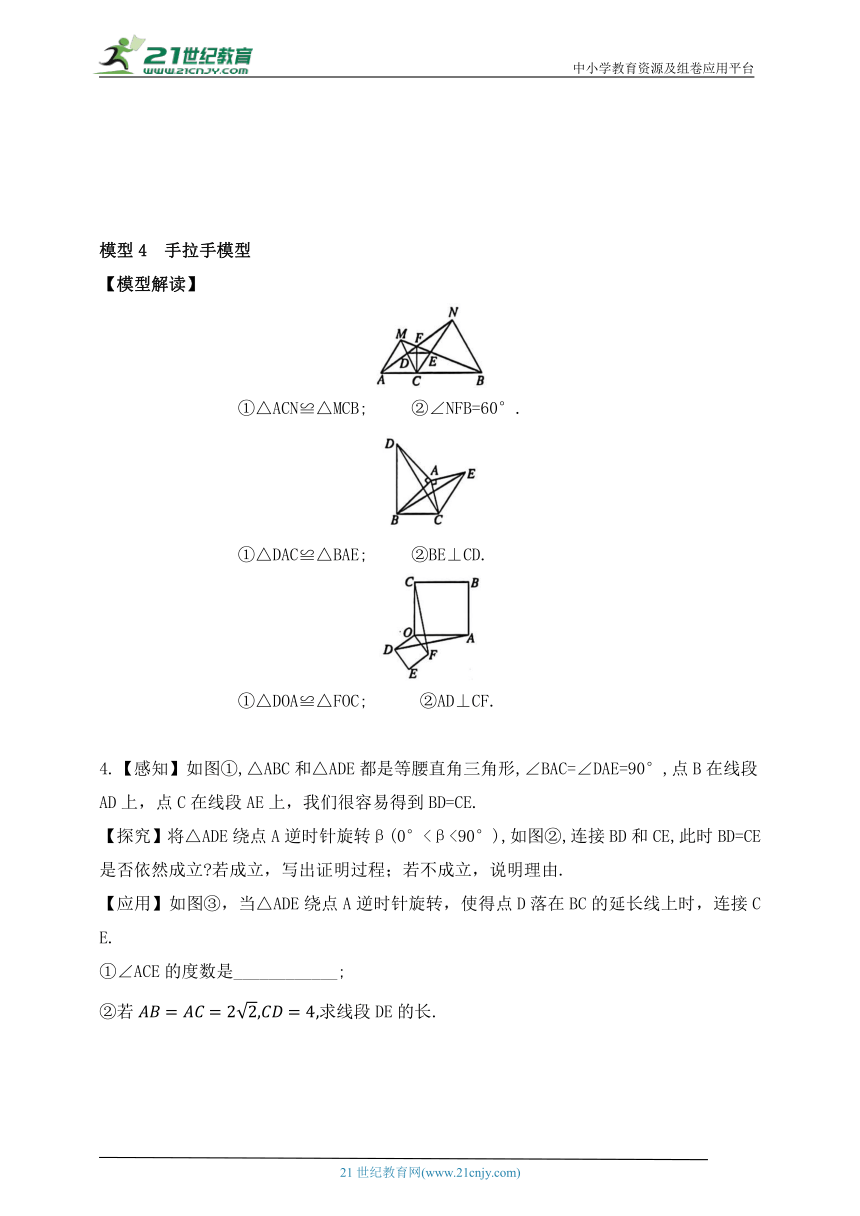
模型1 半角(45°角)模型
【模型解读】
①△AEF≌△AEG; ②EF=DF+BE.
1.(1)如图①,在正方形ABCD中,E是CD边上一点,将△ADE绕点A顺时针旋转90°得到△ABF,观察可知,与DE相等的线段是___________,与∠AFB相等的角是____________;
(2)如图②,在正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,猜想线段DQ,BP,PQ之间的数量关系,并证明;
(3)在图②中,连接BD分别交AP,AQ于点M,N,请直接写出BM,DN,MN之间的数量关系.
模型2 “互补”模型
【模型解读】如图,已知∠AOB=∠DCE=90°,OC平分∠AOB.
①CD=CE; ②OD+OE=OC;
2.如图,∠AOB=90°,OC平分∠AOB,以C为顶点作∠DCE=90°,交OA于点D,交OB于点E.
(1)求证:CD=CE;
(2)若OC=3,求OD+OE的长.
模型3 一线三等角模型模型4手拉手模型
【模型解读】如图,△ABC为等腰直角三角形,AD⊥DE,CE⊥DE.
△ABD≌△BCE, DE=AD+CE.
3.如图①,在△ABC中,∠BAC=90°,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)求证:DE=BD+CE.
(2)若将△ABC绕点A旋转至图②的位置,其他条件不变,DE与BD,CE的关系如何 请予以证明.
模型4 手拉手模型
【模型解读】
①△ACN≌△MCB; ②∠NFB=60°.
①△DAC≌△BAE; ②BE⊥CD.
①△DOA≌△FOC; ②AD⊥CF.
4.【感知】如图①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE.
【探究】将△ADE绕点A逆时针旋转β(0°<β<90°),如图②,连接BD和CE,此时BD=CE是否依然成立 若成立,写出证明过程;若不成立,说明理由.
【应用】如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上时,连接CE.
①∠ACE的度数是____________;
②若求线段DE的长.
5.如图,A是线段BC上一点,△ABD和△ACE都是等边三角形.
(1)如图①,连接BE,CD,求证:BE=CD.
(2)如图②,将△ABD绕点A顺时针旋转得到△AB'D'.
①当旋转角为____________°时,边AD'落在边AE上.
②在①的条件下,延长DD'交CE于点P,连接BD',CD',请写出当线段AB,AC满足什么数量关系时,△BDD'与△CPD'全等 并给予证明.
模型5 费马点模型
【模型解读】如图,
点M为内任意一点,连接AM,BM,CM,当M与三个顶点连线的夹角为120°时,MA+MB+MC的值最小.
6.背景材料:在所在平面上求一点P,使它到三角形的三个顶点的距离之和最小.这个问题是法国数学家费马向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”.如图①,当△ABC三个内角均小于120°时,费马点P在△ABC内部,当∠APB=∠APC=∠CPB=120°时,PA+PB+PC取得最小值.
(1)如图①,将△BPC绕点B顺时针旋转60°得到△BDE,连接PD,可得△BPD为等边三角形,故PD=PB,由旋转可得DE=PC,因此PA+PB+PC=PA+PD+DE,由_______________可知,PA+PB+PC的最小值与线段的_____________长度相等;
(2)如图②,在直角三角形ABC内部有一动点P,∠BAC=90°,∠ACB=30°,连接PA,PB,PC,若AB=2,求PA+PB+PC的最小值.
参考答案
1.【解】(1)BF;∠AED,∠BAE
(2)DQ+BP=PQ.
证明:在正方形ABCD中,∠ADC=∠ABC=90°.
如图①,将△ADQ绕点A顺时针旋转90°得到△ABE,则∠D=∠ABE=90°.
∴∠ABE+∠ABP=180°.∴E,B,P三点共线.
由旋转的性质知∠EAQ=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,∴∠PAE=45°.∴∠PAQ=∠PAE.
在△APE和△APQ中
∴△APE≌△APQ.∴PE=PQ.
∵PE=PB+BE=PB+DQ,∴DQ+BP=PQ.
(3)BM +DN =MN .【点拨】如图②,将△ADN绕点A顺时针旋转90°得到△ABK,连接KM.
∵四边形ABCD为正方形,∴∠ABD=∠ADB=45°.
由旋转的性质得∠NAK=90°,∠ABK=∠ADN=45°,BK=DN,AK=AN.
∵∠PAQ=45°,∴∠MAK=45°.∴∠PAQ=∠MAK.
在△AMN和△AMK中∴△AMN≌△AMK.∴MN=MK.
为直角三角形.
2.(1)【证明】如图,过点C作CG⊥OA于点G,作CH⊥OB于点H.
∵OC平分∠AOB,∴CG=CH.
∵∠AOB=90°,∠DCE=90°,∴∠CDO+∠CEO=180°.B
又∵∠CDG+∠CDO=180°,∴∠CDG=∠CEO.
又∵∠CGD=∠CHE=90°,∴△CDG≌△CEH(AAS).∴CD=CE.
(2)【解】由(1)得△CDG≌△CEH,∴DG=HE.
由题易得CH=OH,CG=OG.
∵CG=CH,∴OG=OH.∴OD+OE=OD+OH+HE=OG+OH=2OH.
设OH=CH=x,在Rt△OCH中,由勾股定理,得(
(负值已舍去),即
3.(1)【证明】∵BD⊥DE,CE⊥DE,∴∠BDA=∠AEC=90°.∴∠BAD+∠ABD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.∴∠CAE=∠ABD.
在△ADB和△CEA中,∴△ADB≌△CEA(AAS).∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
(2)【解】CE=BD+DE.
证明:由题意得∠BDA=∠AEC=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
又∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ADB和△CEA中∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.∴CE=AD=AE+DE=BD+DE.
4.【解】【探究】BD=CE依然成立.证明如下:
∵△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠BAD=∠CAE.∴△ABD≌△ACE(SAS).∴BD=CE.
【应用】①45°
易知△ACE≌△ABD,∴CE=BD=BC+CD=4+4=8.
易知∠BCE=90°,∴∠ECD=90°.
5.(1)【证明】∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°.
∴∠BAD+∠DAE=∠CAE+∠DAE,即∠BAE=∠DAC.
∴△BAE≌△DAC(SAS).∴BE=CD.
(2)【解】①60
②当AC=2AB时,△BDD'与△CPD'全等.
证明:易知∠ABD=60°.
由旋转和等边三角形的性质可知AB=BD=DD'=AD',∴四边形ABDD'是菱形.
∥
∵△ACE是等边三角形,∴AC=AE=CE,∠ACE=60°
∵AC=2AB,∴AE=2AD'.
又∵DP∥BC,∴∠BD'D=∠ABD'=∠DBD'=30°=
∴BD'=CD'.∴△BDD'≌△CPD'(ASA).
6.【解】(1)两点之间线段最短;AE
(2)如图,将△ABP绕点B顺时针旋转60°得到△EBF,连接PF,CE,AE,作EH⊥CA交CA的延长线于点H.
∵在Rt△ABC中,∠ACB=30°,AB=2,∴BC=2AB=4.∴AC=.
由旋转的性质可知PA=EF,∠PBF=∠ABE=60°,PB=BF,AB=BE,
∴△PBF,△ABE是等边三角形.
∴PF=PB,∠BAE=60°,AE=AB=2,∴PA+PB+PC=EF+PF+PC.
∵EF+PF+PC≥CE,∴当C,P,F,E四点共线时,PA+PB+PC的值最小.
∵∠BAC=90°,∠BAE=60°,
∵EH⊥AH,AE=AB=2,∴EH=AE=1.
∴PA+PB+PC的最小值为2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十三章 旋转
专题 旋转中的常见几何模型
模型1 半角(45°角)模型
【模型解读】
①△AEF≌△AEG; ②EF=DF+BE.
1.(1)如图①,在正方形ABCD中,E是CD边上一点,将△ADE绕点A顺时针旋转90°得到△ABF,观察可知,与DE相等的线段是___________,与∠AFB相等的角是____________;
(2)如图②,在正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,猜想线段DQ,BP,PQ之间的数量关系,并证明;
(3)在图②中,连接BD分别交AP,AQ于点M,N,请直接写出BM,DN,MN之间的数量关系.
模型2 “互补”模型
【模型解读】如图,已知∠AOB=∠DCE=90°,OC平分∠AOB.
①CD=CE; ②OD+OE=OC;
2.如图,∠AOB=90°,OC平分∠AOB,以C为顶点作∠DCE=90°,交OA于点D,交OB于点E.
(1)求证:CD=CE;
(2)若OC=3,求OD+OE的长.
模型3 一线三等角模型模型4手拉手模型
【模型解读】如图,△ABC为等腰直角三角形,AD⊥DE,CE⊥DE.
△ABD≌△BCE, DE=AD+CE.
3.如图①,在△ABC中,∠BAC=90°,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)求证:DE=BD+CE.
(2)若将△ABC绕点A旋转至图②的位置,其他条件不变,DE与BD,CE的关系如何 请予以证明.
模型4 手拉手模型
【模型解读】
①△ACN≌△MCB; ②∠NFB=60°.
①△DAC≌△BAE; ②BE⊥CD.
①△DOA≌△FOC; ②AD⊥CF.
4.【感知】如图①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE.
【探究】将△ADE绕点A逆时针旋转β(0°<β<90°),如图②,连接BD和CE,此时BD=CE是否依然成立 若成立,写出证明过程;若不成立,说明理由.
【应用】如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上时,连接CE.
①∠ACE的度数是____________;
②若求线段DE的长.
5.如图,A是线段BC上一点,△ABD和△ACE都是等边三角形.
(1)如图①,连接BE,CD,求证:BE=CD.
(2)如图②,将△ABD绕点A顺时针旋转得到△AB'D'.
①当旋转角为____________°时,边AD'落在边AE上.
②在①的条件下,延长DD'交CE于点P,连接BD',CD',请写出当线段AB,AC满足什么数量关系时,△BDD'与△CPD'全等 并给予证明.
模型5 费马点模型
【模型解读】如图,
点M为内任意一点,连接AM,BM,CM,当M与三个顶点连线的夹角为120°时,MA+MB+MC的值最小.
6.背景材料:在所在平面上求一点P,使它到三角形的三个顶点的距离之和最小.这个问题是法国数学家费马向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”.如图①,当△ABC三个内角均小于120°时,费马点P在△ABC内部,当∠APB=∠APC=∠CPB=120°时,PA+PB+PC取得最小值.
(1)如图①,将△BPC绕点B顺时针旋转60°得到△BDE,连接PD,可得△BPD为等边三角形,故PD=PB,由旋转可得DE=PC,因此PA+PB+PC=PA+PD+DE,由_______________可知,PA+PB+PC的最小值与线段的_____________长度相等;
(2)如图②,在直角三角形ABC内部有一动点P,∠BAC=90°,∠ACB=30°,连接PA,PB,PC,若AB=2,求PA+PB+PC的最小值.
参考答案
1.【解】(1)BF;∠AED,∠BAE
(2)DQ+BP=PQ.
证明:在正方形ABCD中,∠ADC=∠ABC=90°.
如图①,将△ADQ绕点A顺时针旋转90°得到△ABE,则∠D=∠ABE=90°.
∴∠ABE+∠ABP=180°.∴E,B,P三点共线.
由旋转的性质知∠EAQ=90°,AE=AQ,BE=DQ.
∵∠PAQ=45°,∴∠PAE=45°.∴∠PAQ=∠PAE.
在△APE和△APQ中
∴△APE≌△APQ.∴PE=PQ.
∵PE=PB+BE=PB+DQ,∴DQ+BP=PQ.
(3)BM +DN =MN .【点拨】如图②,将△ADN绕点A顺时针旋转90°得到△ABK,连接KM.
∵四边形ABCD为正方形,∴∠ABD=∠ADB=45°.
由旋转的性质得∠NAK=90°,∠ABK=∠ADN=45°,BK=DN,AK=AN.
∵∠PAQ=45°,∴∠MAK=45°.∴∠PAQ=∠MAK.
在△AMN和△AMK中∴△AMN≌△AMK.∴MN=MK.
为直角三角形.
2.(1)【证明】如图,过点C作CG⊥OA于点G,作CH⊥OB于点H.
∵OC平分∠AOB,∴CG=CH.
∵∠AOB=90°,∠DCE=90°,∴∠CDO+∠CEO=180°.B
又∵∠CDG+∠CDO=180°,∴∠CDG=∠CEO.
又∵∠CGD=∠CHE=90°,∴△CDG≌△CEH(AAS).∴CD=CE.
(2)【解】由(1)得△CDG≌△CEH,∴DG=HE.
由题易得CH=OH,CG=OG.
∵CG=CH,∴OG=OH.∴OD+OE=OD+OH+HE=OG+OH=2OH.
设OH=CH=x,在Rt△OCH中,由勾股定理,得(
(负值已舍去),即
3.(1)【证明】∵BD⊥DE,CE⊥DE,∴∠BDA=∠AEC=90°.∴∠BAD+∠ABD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.∴∠CAE=∠ABD.
在△ADB和△CEA中,∴△ADB≌△CEA(AAS).∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
(2)【解】CE=BD+DE.
证明:由题意得∠BDA=∠AEC=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.
又∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ADB和△CEA中∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.∴CE=AD=AE+DE=BD+DE.
4.【解】【探究】BD=CE依然成立.证明如下:
∵△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠BAD=∠CAE.∴△ABD≌△ACE(SAS).∴BD=CE.
【应用】①45°
易知△ACE≌△ABD,∴CE=BD=BC+CD=4+4=8.
易知∠BCE=90°,∴∠ECD=90°.
5.(1)【证明】∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠CAE=60°.
∴∠BAD+∠DAE=∠CAE+∠DAE,即∠BAE=∠DAC.
∴△BAE≌△DAC(SAS).∴BE=CD.
(2)【解】①60
②当AC=2AB时,△BDD'与△CPD'全等.
证明:易知∠ABD=60°.
由旋转和等边三角形的性质可知AB=BD=DD'=AD',∴四边形ABDD'是菱形.
∥
∵△ACE是等边三角形,∴AC=AE=CE,∠ACE=60°
∵AC=2AB,∴AE=2AD'.
又∵DP∥BC,∴∠BD'D=∠ABD'=∠DBD'=30°=
∴BD'=CD'.∴△BDD'≌△CPD'(ASA).
6.【解】(1)两点之间线段最短;AE
(2)如图,将△ABP绕点B顺时针旋转60°得到△EBF,连接PF,CE,AE,作EH⊥CA交CA的延长线于点H.
∵在Rt△ABC中,∠ACB=30°,AB=2,∴BC=2AB=4.∴AC=.
由旋转的性质可知PA=EF,∠PBF=∠ABE=60°,PB=BF,AB=BE,
∴△PBF,△ABE是等边三角形.
∴PF=PB,∠BAE=60°,AE=AB=2,∴PA+PB+PC=EF+PF+PC.
∵EF+PF+PC≥CE,∴当C,P,F,E四点共线时,PA+PB+PC的值最小.
∵∠BAC=90°,∠BAE=60°,
∵EH⊥AH,AE=AB=2,∴EH=AE=1.
∴PA+PB+PC的最小值为2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
