第二十三章《旋转》综合素质评价(含答案)
文档属性
| 名称 | 第二十三章《旋转》综合素质评价(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-26 15:07:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十三章综合素质评价
[时间:60分钟 分值:100分]
一、选择题(每题3分,共21分)
1.将如图所示的圆形图案以圆心为中心,旋转180°)°后得到的图案是( )
2.搭载神舟十九号载人飞船的长征二号F遥十九运载火箭于2024年10月30日成功发射升空,3名航天员开启太空之旅,展现了中国航天科技的新高度.下列图标中,其文字上方的图案是中心对称图形的是( )
3.已知点A(a,-2),B(3,b)关于原点对称,则a-b的值为( )
A.3 B.-1 C.-5 D.-3
4.如图,在平面直角坐标系中,△ABC与△A B C 关于点M(0,-1)成中心对称.已知点B的坐标为(-2,2),则点B 的坐标是( )
A.(2,-2) B.(1,-3) C.(4,-2) D.(2,-4)
5.如图,在等边三角形ABC中,AB=6,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,D是AC边的中点,连接DQ,则DQ的最小值是( )
D.
6.函数的图象分别与x轴、y轴交于A,B两点,线段AB绕点B旋转90°得到线段BC,则点C的坐标为( )
A.(6,2)或(-2,-2) B.(4,-2) C.(4,2) D.(-4,2)或(4,6)
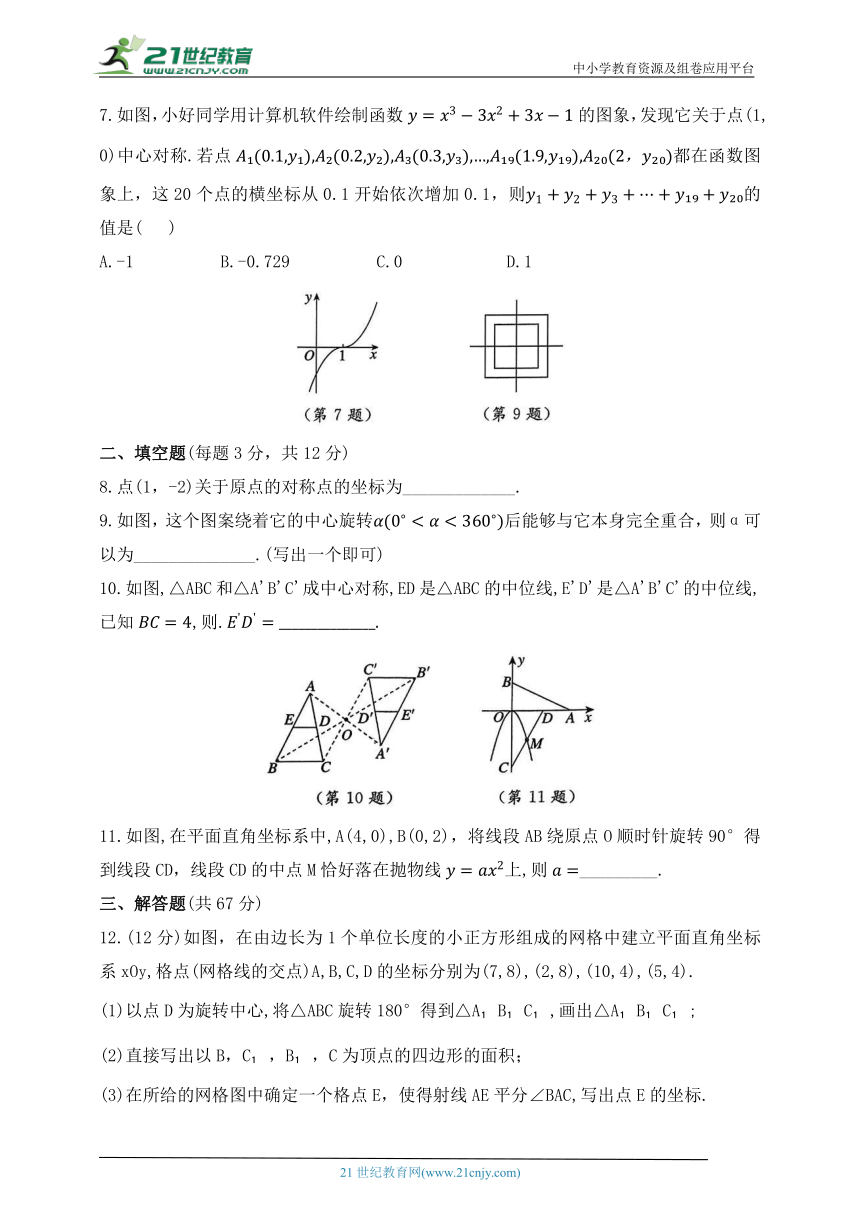
7.如图,小好同学用计算机软件绘制函数的图象,发现它关于点(1,0)中心对称.若点都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则的值是( )
A.-1 B.-0.729 C.0 D.1
二、填空题(每题3分,共12分)
8.点(1,-2)关于原点的对称点的坐标为_____________.
9.如图,这个图案绕着它的中心旋转后能够与它本身完全重合,则α可以为______________.(写出一个即可)
10.如图,△ABC和△A'B'C'成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线,已知,则.
11.如图,在平面直角坐标系中,A(4,0),B(0,2),将线段AB绕原点O顺时针旋转90°得到线段CD,线段CD的中点M恰好落在抛物线上,则_________.
三、解答题(共67分)
12.(12分)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4).
(1)以点D为旋转中心,将△ABC旋转180°得到△A B C ,画出△A B C ;
(2)直接写出以B,C ,B ,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点E,使得射线AE平分∠BAC,写出点E的坐标.
13.(16分)如图,已知 ABCD的对称中心是原点O,且A(-2,1),B(-3,-2).
(1)求点C,D的坐标;
(2)求 ABCD的面积.
14.(18分)如图,在正方形ABCD中,AB=2,对角线AC与BD相交于点O,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,点F恰好落在线段CD上,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求(的最小值.
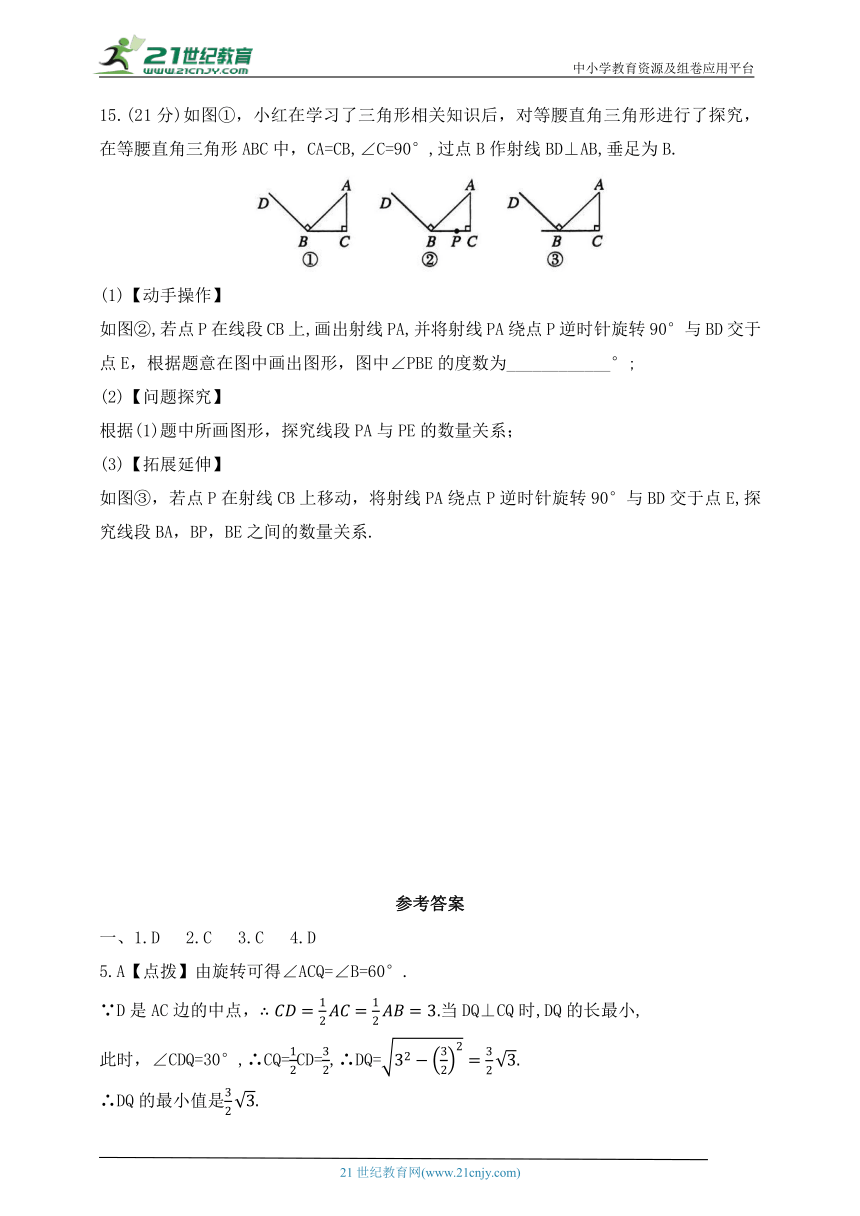
15.(21分)如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为____________°;
(2)【问题探究】
根据(1)题中所画图形,探究线段PA与PE的数量关系;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系.
参考答案
一、1.D 2.C 3.C 4.D
5.A【点拨】由旋转可得∠ACQ=∠B=60°.
∵D是AC边的中点,当DQ⊥CQ时,DQ的长最小,
此时,∠CDQ=30°,∴CQ=CD=,∴DQ=
∴DQ的最小值是
6.D【点拨】当y=0时,-2x+4=0,解得x=2,∴点A的坐标为(2,0).
∴OA=2.当x=0时,y=-2×0+4=4,∴点B的坐标为(0,4).∴OB=4.
如图,将△OAB绕点B顺时针旋转90°得到△O'CB.由旋转知,
∴易得点C的坐标为(-4,2).将△OAB绕点B逆时针旋转90°得到△O'C'B,
由旋转知(O'B=OB=4,O'C'=OA=2,∴易得点C'的坐标为(4,6).
综上所述,点C的坐标为(-4,2)或(4,6).
7.D【点拨】∵图象关于点(1,0)中心对称,y +y =y +y .∵A (1,0),∴y =0.在中,当x=2时,
二、8.(-1,2)9.90°(答案不唯一) 10.2
11.—2【点拨】∵A(4,0),B(0,2),将线段AB绕原点O顺时针旋转90°得到线段CD,∴易得C(0,-4),D(2,0).
∵M是线段CD的中点,∴M(1,-2).
∵M恰好落在抛物线上,∴a=-2.
三、12.【解】(1)△A B C 如图所示.
(2)以B,C ,B ,C为顶点的四边形的面积为40.
(3)如图,点E即为所求,点E的坐标为(6,6).(答案不唯一)
13.【解】(1)∵ ABCD的对称中心是原点O,A(-2,1),B(-3,-2),
∴C(2,-1),D(3,2).
(2)设直线AB的解析式为y=kx+b,
把点A(-2,1),B(-3,-2)的坐标分别代入y=kx+b,得解得
∴直线AB的解析式为y=3x+7.∴当y=0时,
又∵点A到x轴的距离为1,点B到x轴的距离为2,
14.(1)【证明】根据旋转可知∠BEF=90°,BE=EF.
∵FH⊥AC,∴∠FHE=90°.
∵四边形ABCD为正方形,∴AC⊥BD.∴∠BOE=∠EHF=90°.
∴∠BEO+∠EBO=∠BEO+∠FEH=90°.∴∠EBO=∠FEH.∴△OBE≌△HEF(AAS).
(2)【解】∵四边形ABCD为正方形,∴易得OA=,∠ACD=45°.
∵△OBE≌△HEF,∴FH=OE=x.
∵∠CHF=90°,∠FCH=45°,
∴△CFH为等腰直角三角形..
∵点E在线段AO上(与端点不重合),
∴当时,OE -CF的最小值为
15.【解】(1)如图①.135
(2)PA=PE.理由如下:
∵CA=CB,∠C=90°,∴∠ABC=∠BAC=45°.
如图②,过点P作PM∥AB交AC于点M,
∴∠MPC=∠ABC=∠BAC=∠PMC=45°.
∴CP=CM,∠AMP=135°=∠PBE.∴CA-CM=CB-CP,即AM=BP.
∵将射线PA绕点P逆时针旋转90°与BD交于点E,
∴∠APE=90°.∴∠EPB=90°-∠APC=∠PAC.
∴△APM≌△PEB(ASA).∴PA=PE.
(3)当点P在线段BC上时,由(2)可知,BE=PM,BP=AM.易知.
.
易知
当点P在线段CB的延长线上时,过点P作PN⊥BC交BE于点N,如图③.
易知∠ABD=90°,∠ABC=45°,
∴△BPN是等腰直角三角形,∠ABP=135°.∴BP=NP,∠PNB=45°.
∴∠PNE=135°=∠ABP,BN=BP.易知∠APE=90°,∴∠EPN=90°-∠APN=∠APB.
∴△EPN≌△APB(ASA).∴EN=BA.
∵BE=EN+BN,∴BE=BA+BP.
综上所述,当点P在线段BC上时,;当点P在线段CB的延长线上时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十三章综合素质评价
[时间:60分钟 分值:100分]
一、选择题(每题3分,共21分)
1.将如图所示的圆形图案以圆心为中心,旋转180°)°后得到的图案是( )
2.搭载神舟十九号载人飞船的长征二号F遥十九运载火箭于2024年10月30日成功发射升空,3名航天员开启太空之旅,展现了中国航天科技的新高度.下列图标中,其文字上方的图案是中心对称图形的是( )
3.已知点A(a,-2),B(3,b)关于原点对称,则a-b的值为( )
A.3 B.-1 C.-5 D.-3
4.如图,在平面直角坐标系中,△ABC与△A B C 关于点M(0,-1)成中心对称.已知点B的坐标为(-2,2),则点B 的坐标是( )
A.(2,-2) B.(1,-3) C.(4,-2) D.(2,-4)
5.如图,在等边三角形ABC中,AB=6,点P是边BC上的动点,将△ABP绕点A逆时针旋转60°得到△ACQ,D是AC边的中点,连接DQ,则DQ的最小值是( )
D.
6.函数的图象分别与x轴、y轴交于A,B两点,线段AB绕点B旋转90°得到线段BC,则点C的坐标为( )
A.(6,2)或(-2,-2) B.(4,-2) C.(4,2) D.(-4,2)或(4,6)
7.如图,小好同学用计算机软件绘制函数的图象,发现它关于点(1,0)中心对称.若点都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则的值是( )
A.-1 B.-0.729 C.0 D.1
二、填空题(每题3分,共12分)
8.点(1,-2)关于原点的对称点的坐标为_____________.
9.如图,这个图案绕着它的中心旋转后能够与它本身完全重合,则α可以为______________.(写出一个即可)
10.如图,△ABC和△A'B'C'成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线,已知,则.
11.如图,在平面直角坐标系中,A(4,0),B(0,2),将线段AB绕原点O顺时针旋转90°得到线段CD,线段CD的中点M恰好落在抛物线上,则_________.
三、解答题(共67分)
12.(12分)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4).
(1)以点D为旋转中心,将△ABC旋转180°得到△A B C ,画出△A B C ;
(2)直接写出以B,C ,B ,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点E,使得射线AE平分∠BAC,写出点E的坐标.
13.(16分)如图,已知 ABCD的对称中心是原点O,且A(-2,1),B(-3,-2).
(1)求点C,D的坐标;
(2)求 ABCD的面积.
14.(18分)如图,在正方形ABCD中,AB=2,对角线AC与BD相交于点O,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,点F恰好落在线段CD上,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求(的最小值.
15.(21分)如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为____________°;
(2)【问题探究】
根据(1)题中所画图形,探究线段PA与PE的数量关系;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系.
参考答案
一、1.D 2.C 3.C 4.D
5.A【点拨】由旋转可得∠ACQ=∠B=60°.
∵D是AC边的中点,当DQ⊥CQ时,DQ的长最小,
此时,∠CDQ=30°,∴CQ=CD=,∴DQ=
∴DQ的最小值是
6.D【点拨】当y=0时,-2x+4=0,解得x=2,∴点A的坐标为(2,0).
∴OA=2.当x=0时,y=-2×0+4=4,∴点B的坐标为(0,4).∴OB=4.
如图,将△OAB绕点B顺时针旋转90°得到△O'CB.由旋转知,
∴易得点C的坐标为(-4,2).将△OAB绕点B逆时针旋转90°得到△O'C'B,
由旋转知(O'B=OB=4,O'C'=OA=2,∴易得点C'的坐标为(4,6).
综上所述,点C的坐标为(-4,2)或(4,6).
7.D【点拨】∵图象关于点(1,0)中心对称,y +y =y +y .∵A (1,0),∴y =0.在中,当x=2时,
二、8.(-1,2)9.90°(答案不唯一) 10.2
11.—2【点拨】∵A(4,0),B(0,2),将线段AB绕原点O顺时针旋转90°得到线段CD,∴易得C(0,-4),D(2,0).
∵M是线段CD的中点,∴M(1,-2).
∵M恰好落在抛物线上,∴a=-2.
三、12.【解】(1)△A B C 如图所示.
(2)以B,C ,B ,C为顶点的四边形的面积为40.
(3)如图,点E即为所求,点E的坐标为(6,6).(答案不唯一)
13.【解】(1)∵ ABCD的对称中心是原点O,A(-2,1),B(-3,-2),
∴C(2,-1),D(3,2).
(2)设直线AB的解析式为y=kx+b,
把点A(-2,1),B(-3,-2)的坐标分别代入y=kx+b,得解得
∴直线AB的解析式为y=3x+7.∴当y=0时,
又∵点A到x轴的距离为1,点B到x轴的距离为2,
14.(1)【证明】根据旋转可知∠BEF=90°,BE=EF.
∵FH⊥AC,∴∠FHE=90°.
∵四边形ABCD为正方形,∴AC⊥BD.∴∠BOE=∠EHF=90°.
∴∠BEO+∠EBO=∠BEO+∠FEH=90°.∴∠EBO=∠FEH.∴△OBE≌△HEF(AAS).
(2)【解】∵四边形ABCD为正方形,∴易得OA=,∠ACD=45°.
∵△OBE≌△HEF,∴FH=OE=x.
∵∠CHF=90°,∠FCH=45°,
∴△CFH为等腰直角三角形..
∵点E在线段AO上(与端点不重合),
∴当时,OE -CF的最小值为
15.【解】(1)如图①.135
(2)PA=PE.理由如下:
∵CA=CB,∠C=90°,∴∠ABC=∠BAC=45°.
如图②,过点P作PM∥AB交AC于点M,
∴∠MPC=∠ABC=∠BAC=∠PMC=45°.
∴CP=CM,∠AMP=135°=∠PBE.∴CA-CM=CB-CP,即AM=BP.
∵将射线PA绕点P逆时针旋转90°与BD交于点E,
∴∠APE=90°.∴∠EPB=90°-∠APC=∠PAC.
∴△APM≌△PEB(ASA).∴PA=PE.
(3)当点P在线段BC上时,由(2)可知,BE=PM,BP=AM.易知.
.
易知
当点P在线段CB的延长线上时,过点P作PN⊥BC交BE于点N,如图③.
易知∠ABD=90°,∠ABC=45°,
∴△BPN是等腰直角三角形,∠ABP=135°.∴BP=NP,∠PNB=45°.
∴∠PNE=135°=∠ABP,BN=BP.易知∠APE=90°,∴∠EPN=90°-∠APN=∠APB.
∴△EPN≌△APB(ASA).∴EN=BA.
∵BE=EN+BN,∴BE=BA+BP.
综上所述,当点P在线段BC上时,;当点P在线段CB的延长线上时,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
